基于SPSS的共现聚类分析参数选择的实例研究
2016-03-21,
,
共现分析是对两个及以上能够表达某一学科领域研究主题或方向的特征项(如主题词、引文、作者等)在同一篇文献中出现的现象进行分析。出现的频次越多,表明这些特征项的关系越密切、距离越近[1]。作为内容分析的常用方法之一,共现分析常与SPSS中的系统聚类分析结合使用[2]。但目前对原始矩阵、相似性度量和类间距离计算方法[3]的选择尚存在争议。
原始矩阵的类型可选择共现矩阵或特征项-来源文献矩阵。共现矩阵是对称矩阵的行列均是特征项,单元格的数字则是行特征项和对应列特征项共同出现的次数;特征项-来源文献矩阵,其行列分别为特征项及其来源文献,若特征项在文献中出现则值为1,否则为0。相似性度量是矩阵标准化的手段,通过度量使得相似者愈加相似,不相似者愈加不相似,用以衡量个体之间的距离。而类间距离计算方法可衡量类与类之间的距离,距离最小的两个小类被合并成为一类。SPSS 提供的类间距离测度方法有组间(内)连接、最大(小)距离和离差平方和法(简称Ward法)等。有研究表明,国内学者应用共现分析的方法存在问题[4]。笔者调研发现,国内学者进行文献聚类共现分析应用最广泛的是共现矩阵。共现矩阵转化为相关矩阵的过程中,最常用的相似系数是ochiai系数,最受欢迎的聚类方法是类间计算方法选择Ward和组间连接法,度量方法为平方欧式距离。词篇矩阵大多选用ochiai系数,聚类方法选择组间或组内联接法。
本文旨在通过实例分析,比较矩阵类型、各种聚类方法和参数之间的差异,以期得到共现聚类分析规范的最佳方法。
1 研究材料与方法
1.1 研究材料
OHSUMED实验集是由使用MEDLINE的新手医生根据106个主题进行检索得出的。他们根据病人的信息以及自己的信息需求,由检索人员检索问题,然后由另一组医生评价检索到的每篇文献与提问之间的相关性,评价等级包括明确相关、可能相关和不相关三个级别。
这些明确相关的提问-文献对可作为我们分类研究的金标准。
1.2 研究方法
1.2.1 收集样本
浏览OHSUMED数据集,从中选择相关文献数据中的5个Queries(以下简称检索主题),见表1。从PubMed数据库中检索,输出各个检索主题的xml格式文件。

表1 各问题明确相关文献分布
1.2.2 处理数据
将OHSUMED数据导入BICOMB[5],选择提取主要主题词-副主题词,生成词篇矩阵和共词矩阵。进一步利用Matlab软件实现共词矩阵的ochiai系数、pearson系数、cosine系数和spearman系数的相似矩阵,转换为相应的相异矩阵,便于聚类分析。
1.2.3 聚类分析
将词篇矩阵和共词相异矩阵输入SPSS进行系统聚类分析。对于词篇矩阵,选择以下系统聚类方法和参数搭配:组间联接法+ochiai[6]、组间联接法+jaccard,最大距离法+ochiai[7]、最大距离法+jaccard,组内联接法+ochiai[8]、组内联接法+jaccard,最小距离法+ochiai、最小距离法+jaccard,将系统聚类的结果导入Excel进行对应类的整理。对于4种共词相似系数处理矩阵和原始共词矩阵,分别以ochiai系数[9]、pearson系数[10]、jaccard系数、cosine系数[11]和原始共词矩阵在SPSS中选择以下系统聚类和参数搭配:Ward法+平方欧氏距离[10]、组间联接法+平方欧氏距离[12]、组内联接法+平方欧氏距离[13]、组间联接法+欧氏距离[14]等,累计20种组配方法。
1.2.4 各种选择组合后聚类效果的评价与比较
本次研究选择的指标主要有基于金标准F值、基于簇F值和熵(Entropy)[15]。
1.2.4.1 基于金标准F值
对于任何人工主题Pj和聚类簇Ci:
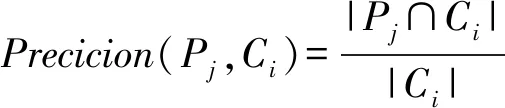


1.2.4.2 基于簇F值
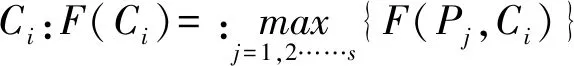
1.2.4.3 熵值
针对语料X上的聚类结果C={C1,C2,…,Cm}中的每一个簇Ci,计算簇Ci的熵。
2 结果与分析
2.1 矩阵处理结果
将检索获得的104篇文献,导入BICOMB进行处理共获得187个主要主题词+主要副主题词,且文献间无重复,并得出共词矩阵和词篇矩阵。
利用Matlab将共词矩阵转化为ochiai系数、pearson系数、spearman系数、cosine系数 4种相关系数矩阵,将相似矩阵转换为相异矩阵,计算公式为:相异矩阵=1-相似矩阵,其中spearman 系数和pearson 系数所得矩阵为负值矩阵。本文采用的是SPSS中的Z得分标准化和重新标度到0-1两种方式进行标准处理。
2.2 SPSS聚类结果
将词篇矩阵和相异(似)矩阵进行SPSS系统聚类,选择上述参数和方法,聚类结果如表2所示。

表2 词篇矩阵组内联接法+ochiai系数聚类群集(部分)
2.3 Matlab计算结果
已知基于金标准(簇)F值越大(0.8左右),熵值越小(0.2左右),聚类结果越好。与所选相关系数相比,词篇矩阵聚类结果受类间距离计算方法的影响更大,最小距离法和组间联接法聚类效果最好,见表3-4。
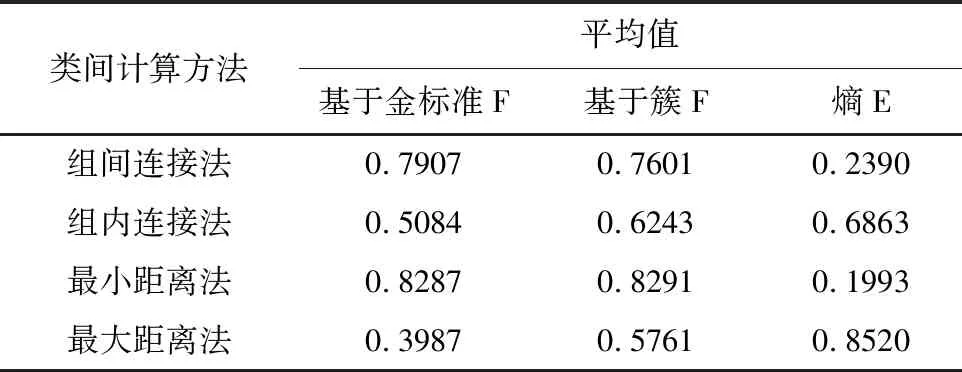
表3 类间计算方法对词篇矩阵结果的影响

表4 相关系数对词篇矩阵聚类结果的影响
相比之下,共词矩阵聚类结果与输入SPSS前所选用的相关系数关系较大,而与聚类过程中选择的参数关系较小,spearman系数和pearson系数、cosine系数聚类效果较好,如表5-表6。

表5 类间计算方法及参数对共词矩阵聚类效果的影响

表6 相关系数对共词矩阵聚类结果的影响
针对每种相似系数的每种聚类评价指标,分别计算其平均得分,如图1所示。从图1可看出,F值最高、熵值最低的是共词矩阵的spearman系数,其次是词篇矩阵的两种系数。从总体趋势看,词篇矩阵的聚类结果较为稳定,共词矩阵聚类效果会因为相似系数的差异而大幅度上下波动。

图1 相似系数聚类结果得分平均值
就总体平均值而言,词篇矩阵得分要优于共现矩阵,见表7。
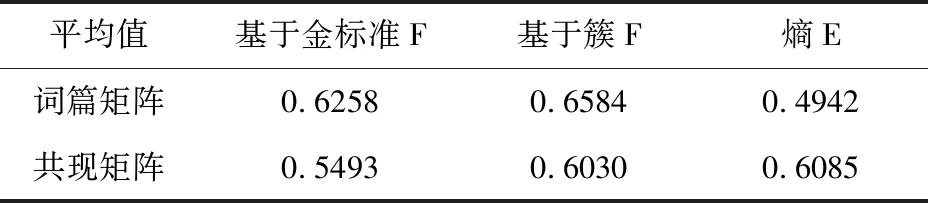
表7 两种矩阵得分平均值
3 讨论
3.1 熵值上下波动的主要原因
熵值波动的主要原因是大类现象。大类现象指人工判定为N类的文档集合,通过系统分析聚类为N类后,无法看到文档在聚类结果中的正确分布,反而看到一个非常大的类和若干小类。如选用ochiai相似系数矩阵、ward法、斐方度量聚类,文中187个主要主题词-副主题词中有166个被囊括在一个大类里,而其他的类里只分别涵盖了5、6、5、5个词。对比可知,该大类涵盖了5个原先分类标准的主题词,因此聚类结果散乱、熵值高。该现象在系统聚类分析中属正常现象,可通过调整聚类类别数以改善聚类结果。
3.2 影响聚类结果的主要因素
3.2.1 矩阵类型
从某种程度上说,共词矩阵是一种相似(相异)矩阵,而词篇矩阵是二值(0,1)阵,每行的数值可看作是该样本的性质变量。实际上,共词矩阵可通过词篇矩阵与其转置矩阵相乘得到,但不少学者认为在转化过程中其信息量有所损失。所以在所得聚类结果中,共词矩阵并不能很好地还原原先类,且结果得分波动幅度很大。
2010年崔雷[16]和赖院根[17]就提出SPSS系统聚类中矩阵类型的思考。SPSS要求输入的是case-variance(样本-变量)形式的矩阵,即词篇矩阵,聚类选项中数据类型选择的是“binary”。目前也有很多学者习惯使用共现矩阵的相似或相异矩阵,虽然可以得出聚类结果,实际上这在原理上是行不通的。相似(相异)矩阵本身就是一种相似距离,如果导入SPSS中按照聚类步骤,数据变换、对象之间的距离计算和层次聚类,计算得到的是“距离的距离”,其聚类结果的正确性尚有待考证。在必须使用共现矩阵进行系统聚类时,可参照文献[3]的方法对算法进行相应修改,避免相似性的重复测量。
3.2.2 相关系数
从结果分析可以看出,相关系数的选择对聚类结果影响较大,尤其是对于共词矩阵。在作者同被引分析方面,Loet Leydesdorff 曾于2006年提出[18],对于对称矩阵(如共词矩阵)不应再使用任何相关性度量,因为其本身已是一种相似(相异)距离。
从原理上看,相关度量可分为相似性度量(如pearson 系数和cosine系数)和相异性度量(如欧几里得距离)。对于不同的矩阵应根据其分布特点选择不同的相关度量。
Pearson相关系数适合用于服从正态分布时且在逻辑范畴内必须是等间距的数据。Cosine系数与ochiai系数原理相同,二者区别在于ochiai系数一般应用于(0,1)矩阵,cosine系数一般用于距离矩阵,但实际应用中,国内学者常将二者混淆,出现如“计算共现矩阵的ochiai系数矩阵”之类的方法。而且cosine相似系数有时易与Jaccard 系数的推广形式Tanimoto系数混淆,也应区别对待。Spearman 秩相关系数应用于对不服从正态分布的数据、原始等级数据、总体分布类型未知的数据,对原始变量分布不作要求。本研究中spearman秩相关系数所的聚类结果较好,因其不符合正态分布,亦非二元变量。欧氏(欧几里得)平方距离是一种相异性度量,SPSS中使用ward法聚类时,要求使用该度量。
对于类间距离计算方法的选择,就本研究结果来看,词篇矩阵最好选择最小距离法或组间联接法,但类间计算方法对相似(异)矩阵的影响不大,使用时应注意结合矩阵特点选择聚类方法。如选用Ward法时应选择欧氏距离平方作为度量。相似(异)数据不宜选用斐方度量等,若选择不当,会对结果产生很大影响,甚至扭曲结果。
4 结语
本文针对国内目前SPSS共现聚类分析常见的问题和争议,对其应用过程中应选择的矩阵类型、相似系数和类间计算方法及其搭配方式进行了研究。SPSS系统聚类的过程中,词篇矩阵比共词矩阵在稳定性和聚类结果方面效果更好,应作为聚类分析的首选矩阵。Spearman系数的适用范围较为广泛,在不可获得词篇矩阵的情况下,对共现矩阵的处理方式应结合其具体分布和相关系数的原理科学选择。
