基于可视化图方法的体征时间序列数据分类分析研究＊

焦晓宇，周雪忠＊＊，胡镜清，谢 琪，周洪伟

（1. 北京交通大学计算机与信息技术学院 交通数据分析与挖掘北京市重点实验室 北京 100044；2. 中国中医科学院中医基础理论研究所 北京 100700；3. 中国中医科学院 北京 100700；4. 中国中医科学院中医中医药数据中心 北京 100700）

基于可视化图方法的体征时间序列数据分类分析研究＊

焦晓宇1，周雪忠1＊＊，胡镜清2，谢 琪3，周洪伟4

（1. 北京交通大学计算机与信息技术学院 交通数据分析与挖掘北京市重点实验室 北京 100044；2. 中国中医科学院中医基础理论研究所 北京 100700；3. 中国中医科学院 北京 100700；4. 中国中医科学院中医中医药数据中心 北京 100700）

目的：本研究采用复杂网络理论研究体征时序数据，使用网络特征刻画体征时序数据的动态特征，分析网络特征与人体生理系统健康状态的关系。方法：本文采用可视化图方法将标准心率时序数据和穿戴设备采集的老年人心率等体征时序数据网络化，提取网络特征，采用决策树分类方法分析网络特征与心脏疾病和年龄因素关系。结果：决策树模型对心脏疾病和年龄因素有较好的分类结果，标准心率时序数据的分形特性使网络度分布为幂律分布，网络图密度特征是与心脏疾病和年龄因素相关的主要因素。结论：网络拓扑结构继承体征时序数据的动态特性并将之体现在网络特征上。体征时序数据的动态特性和网络特征的对应关系还待进一步研究阐明。

时间序列 复杂网络 网络特征 生理体征 老年健康

时间序列数据是按时间顺序记录的数据点，是复杂系统的数据反映。时间序列挖掘将时间序列数据作为研究对象，以挖掘时间序列数据的稳定性、变异性等特性[1-3]。时间序列数据挖掘方法通常以特征表示和相似性度量为基础，然后进行分类、聚类、兴趣模式发现、异常模式发现、数据可视化等挖掘分析[2,4]。

根据复杂系统产生的时间序列数据来评价系统的状态，是时间序列数据研究的重要研究内容，研究人员已经对此经过大量的研究，并在金融、医学、气象等领域取得了很大进步。例如，Costa M.等[4]提出多尺度熵的方法，在多个尺度上计算时间序列数据的熵值，用多尺度熵值来评价复杂系统的复杂性，并将多尺度熵算法应用到人体生理系统评价中。Lacasa L.等[5]提出将复杂系统的时间序列数据转化为网络，通过分析网络模体将不同性质的复杂系统进行类目划分[6,7,9]，他们发现健康状态不同者的心率时间序列网络具有不同的模体结构。Zhang J.等[8]提出将周期性时间序列数据转化为网络的方法，探讨网络拓扑结构和复杂系统动态特性的关系。

时间序列数据的网络化将复杂网络的理论引入到时间序列数据的挖掘分析中，以网络拓扑结构为基础，探讨网络特征和复杂系统之间的关系。本文利用时间序列数据网络化方法（Visibility Graph，VG）将时间序列数据转化为网络[5]，抽取网络特征作为时间序列数据的特征，结合机器学习的方法，探讨了复杂系统特性评价的网络化方法。文中选取人体心脏系统作为复杂系统，以心率时间序列数据为研究对象，分析了心率数据VG网络的度分布特性，并采用监督分类模型进行心率时序数据网络和心脏健康状态关系模型的学习。

1 方法

1.1 可视化图方法

可视化图方法VG的出发点是利用复杂网络技术分析时间序列数据，探索时间序列数据结构特性与网络特征的关系。首先是将时间序列数据转换为网络，转换方式是将每一个数据点作为网络的一个节点，节点间的边满足下列要求：

①相邻的节点之间有边相连；

②两个数据点A＜ta，ya＞；B＜tb，yb＞；对于A、B间的任意数据点C＜tc，yc＞满足：

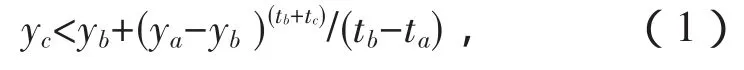
则节点A、B可见，A、B有边连接[5,9]。

VG算法将时间序列数据转化为网络，网络将继承时间序列数据的时间和空间特性，并将这些特性体现在网络的拓扑结构中，因此不同性质的时间序列数据对应的VG网络具有不同的网络拓扑结构。对于周期时间序列数据，VG网络继承时间序列数据的周期特性成为规则网络，整个网络是一个周期内数据点形成的网络的重复组合。

随机网络转化为VG网络后，较大的数据点具有更高的可见性，成为hub节点，使网络的度分布成为指数函数，网络是随机网络，如图1所示。我们生成了一个具有10 000个数据点的随机时间序列，图1（a）为随机时间序列的点线图，图1（b）为对应VG网络的度分布，可见度分布为指数分布。

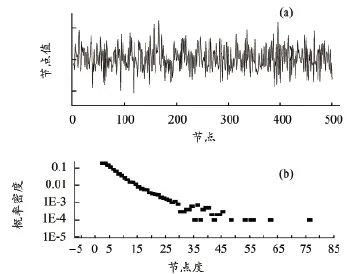
图1 随机数据及其生成的VG网络的度分布

分形时间序列数据具有自相似的特性，其生成的VG网络度分布具有幂律分布的特征，网络为无标度网络，如图2所示[9]。我们生成了一个具有10 000个数据点的Conway序列，Conway序列为：

1.2 网络特征

我们采用VG算法将时间序列数据转化为网络，进一步抽取网络拓扑特征作为复杂系统的特征。我们选择度分布、最大度、图密度、集聚系数、全局集聚系数、介数分布、模块度和特征路径长度（Average Path Length，APL）这7个特征[10,11]。

度分布是指网络中节点度的分布，不同性质的网络度分布函数不同，随机网络、WS小世界网络、NW小世界网络的度分布近似泊松分布，无标度网络的度分布为幂律分布。无标度网络的幂律分布和时间序列数据分形特性间存在某种联系[10]。最大度即为网络中节点度的最大值，对于一个具有n个节点网络，最大度为k的概率hk为：

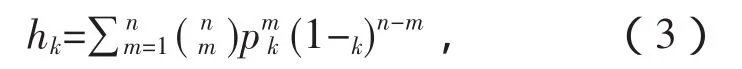
其中pk为度值为k的概率，Pk为度分布的累积分布在k的值。最大度和时间序列数据的极值和最值有关，是产生hub节点的重要因素。

图密度表示网络中各节点之间联系的紧密程度，无向图图密度D的定义为：

图2 Conway时间序列数据和其VG网络度分布

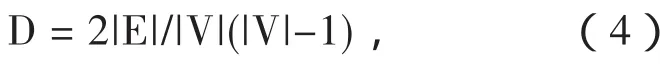
时序数据VG网络的图密度和时序数据的变动率有关。时序数据的变动率越大，时序数据节点间的可见性越高，时序数据生成的VG网络图密度越大。传递特性评价网络中三角形的密度，在社交网络中表示一个人的朋友的朋友也是其朋友，传递特性随着网络规模的增加趋向于非零极限。特征路径长度为网络中任意两个节点之间的距离的平均值，一些节点数巨大的网络的特征路径长度却很小。模块度的概念最早由Mark Newman提出，用来衡量网络社区结构强度，在iGraph中采用基于贪心思想的模块度最大化贪心算法FN进行模块度计算。

1.3 C4.5决策树

决策树是一个用于监督学习的层次预测分类模型，表示对象属性与对象值之间的一种映射关系。决策树使用树状图形或决策模型，着眼于从一组无规则的事例推理出决策树表示形式的分类规则。树中每个非叶子节点表示某个对象属性，而每个分叉路径则代表某个可能的属性值，每个叶节点则对应从根节点到该叶节点的路径所示对象的值。决策树的训练时间相对较少，树形的分类模型比较符合人类的理解方式[12]。

C4.5算法是最常用、最有影响的决策树算法之一，是改良的ID3算法[13]。C4.5算法基于生成的决策树中节点所含的信息熵最小的原理，采用信息增益比作为选择测试属性的标准，能够处理离散值属性和连续值属性。

2 标准心率数据分析

心率数据具有较快的频率且方便采集，是研究人员常用的一种时间序列数据。我们选取了3种类型的心率数据，分别对应健康人（Normal Sinus Rhythm，NSR）、充血性心率衰竭患者（Congestive Heart Failure，CHF）和房颤患者（Atrial Fibrillation，AF）。然后从Physionet上下载了对应的数据样本，其中包含NSR样本54个，CHF患者样本29个，AF患者样本70人，其中NSR和CHF患者的采集时间约为23 h，AF患者采集时间约为1 min[14]。

由于房颤心率的采集时间较短，为了平衡样本的差异，我们将NSR和CHF的心率数据进行了拆分，将样本每隔6 h进行一次拆分，拆分出来的时间序列数据作为一个独立的样本，最终得到106个充血性心率衰竭的心率样本和176个健康的心率样本,样本心率时序数据如图3所示。

对于得到的样本，我们采用VG算法将心率时序数据转换为心率网络，并用iGraph计算了网络最大度、度分布、图密度、集聚系数、全局集聚系数、介数分布、模块度和特征路径长度这7个特征[15]，其中度分布指数、图密度、集聚系数的分布如图4所示。

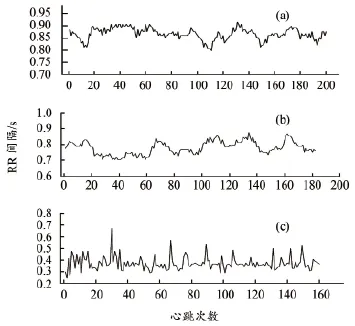
图3 心率时序数据

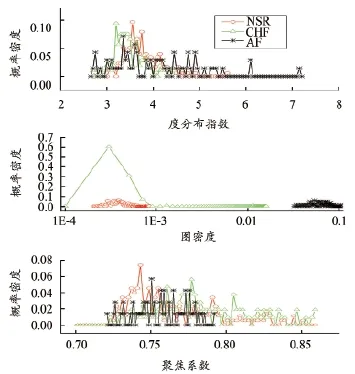
图4 网络特征数据的分布

其中对于网络的度分布，我们进行了幂律分布的拟合[16]，如图5所示。图5（a）为NSR心率VG网络度分布，符合参数α=2.02的幂律分布。图5（b）为CHF患者的心率VG网络，符合参数α=2.26的幂律分布。图5（c）为AF患者的心率VG网络，符合参数α=2.02的幂律分布。可见，这3个网络的度分布都满足幂律分布，说明VG网络继承了心率时序数据的分形特性。

我们将心率时序数据的网络拓扑特征作为数据集特征，将心脏健康状况作为类别，采用C4.5决策树算法进行了学习[12,13]。首先我们将3种类型的心率数据汇总在一起，形成一个多类分类数据集，进行了C4.5算法的训练学习。分类结果如图表1所示，平均准确率为0.73，平均召回率为0.739。然后我们将NSR和CHF患者构成一个样本集，采用C4.5决策树算法进行了学习，模型的分类结果如图表2所示，平均准确率为0.667，平均召回率为0.670。最后我们对由NSR和AF患者构成的数据集进行了C4.5学习，分类结果如图表3所示，平均准确率为0.996，平均召回率为0.996。

上述结果表明，不同健康状态的心率时序数据对应的VG网络拓扑结构和网络特征存在区别，其中与NSR相比，AF患者心率对应的VG网络具有较好的区分性。Costa M等[3,4]的结果表明AF患者心率数据的多尺度熵曲线和白噪声的多尺度熵曲线是一致的，表明AF患者的心率数据具有较高的随机性，而NSR和CHF患者的心率数据具有较高的确定性。AF患者心率数据和NSR、CHF患者心率数据的动态特性不同，因此具有较高的区分性。同时也说明VG网络继承时序数据的动态特性，并将动态特性体现在网络的拓扑结构和网络特征上。

在学习到的3个模型中，3种类型心率数据学习到的决策树模型如图6所示，其中0代表NSR人群，1代表AF人群，2代表CHF人群。3个决策树模型选择出来的主要属性是图密度、度分布和集聚系数。由图6可见，AF患者心率数据对应VG网络的图密度比其他两类心率数据VG网络的图密度高，说明AF患者的心率比NSR和心衰患者心率的变动率高。

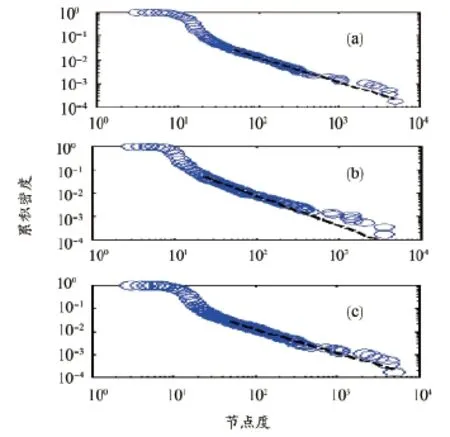
图5 度分布的幂律函数拟合

3 老年人心率等体征数据分析

物联网时代可穿戴设备的常规应用将给疾病诊断机理研究和健康管理带来新的机遇。相对于传统的医疗设备，可穿戴医疗设备具有更便捷的体征时序数据采集能力，这为解决我国日益加重的人口老龄化现象带来的老年人健康问题提供了新的解题方式。

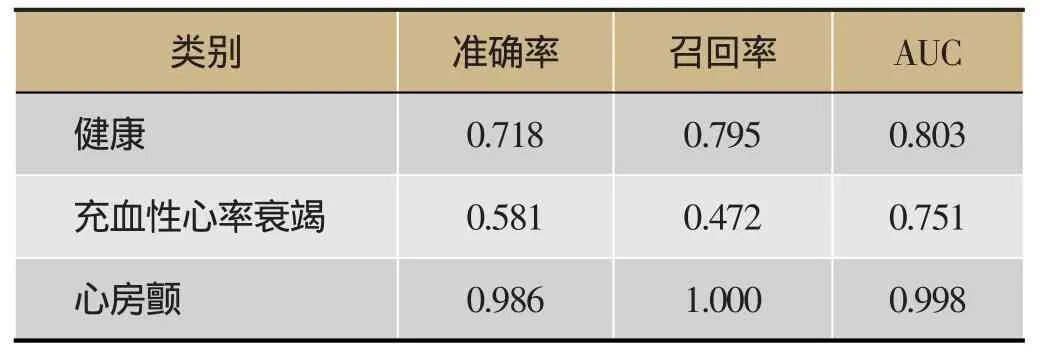
表1 NSR、CHF、AF分类结果

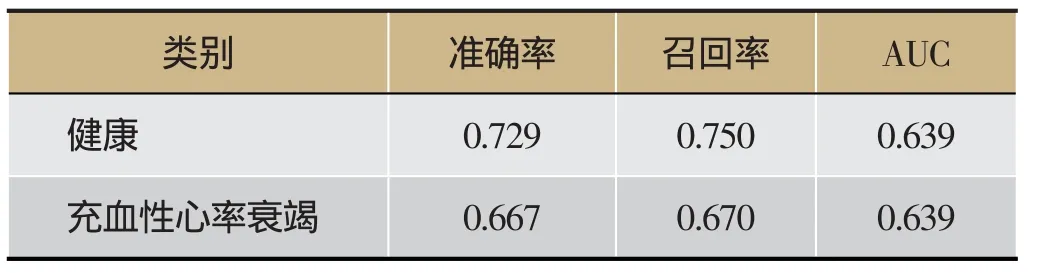
表2 NSR、CHF分类结果

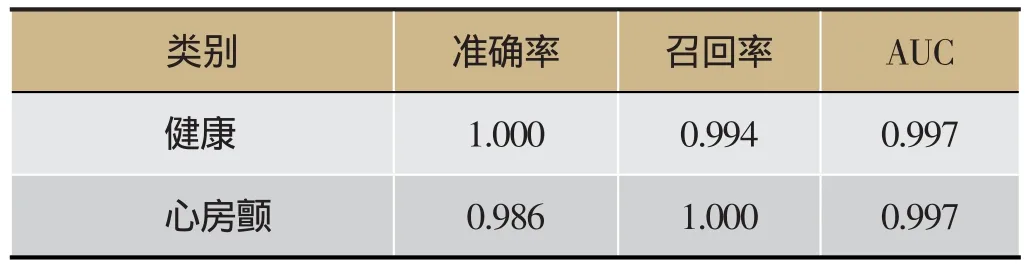
表3 MSR、AF分类结果

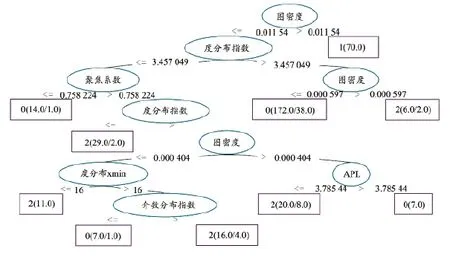
图6 心率数据决策树模型

可穿戴设备不同于专业的医疗设备，其采集的体征时序数据能否作为疾病诊断的标准还有待讨论，对此我们进行了尝试性的探索。我们利用穿戴设备采集65位老年人和10位青年人的心率、动脉血氧饱和度、体温和呼吸频率数据，采集时间为24 h。我们对采集的数据进行了初步的筛选，最终得到可用样本34个，其中包含24位老年人和10位青年人，每个样本的不间断采集点数量在2 000个以上，心率数据如图7所示。

我们将年龄作为分析对象，考察老年人和青年人两个年龄组的体征时序数据VG网络的区别。对于每个体征时序数据，我们采用可视图方法生成了VG网路，并计算了VG网络的各个特征值。我们采集了每个样本的心率、动脉血氧饱和度、体温和呼吸频率4个体征数据，从34个可用的样本，最终得到体征时序数据VG网络136个。将老年人和青年人分成两组，老年人组包含VG网络96个，青年人组包含VG网络40个。采用C4.5分类算法进行学习，分类模型如图8所示，其中1代表老年人，2代表青年人，分类结果如表4所示，平均分类准确率为0.758，平均召回率为0.743。

由上述模型可见，和年龄相关的主要网络特征是图密度、模块度、度分布和全局集聚系数。在图密度上，老年人心率、呼吸频率、体温和动脉血氧饱和度体征时序数据VG网络的图密度大于青年人体征时序数据VG网络的图密度，说明老年人体征数据的变动率较高，老年人对人体体征的调节能力较低。在心率、呼吸频率、体温和动脉血氧饱和度这4个体征时序数据中，动脉血氧饱和度比其他3个体征更为稳定，每位受试者各项体征时序数据VG网络的图密度值如图9所示，可见动脉血氧饱和度VG网络的图密度比其他3个体征时序数据VG网络的图密度低。

图7 CIM设备采集的数据（部分）

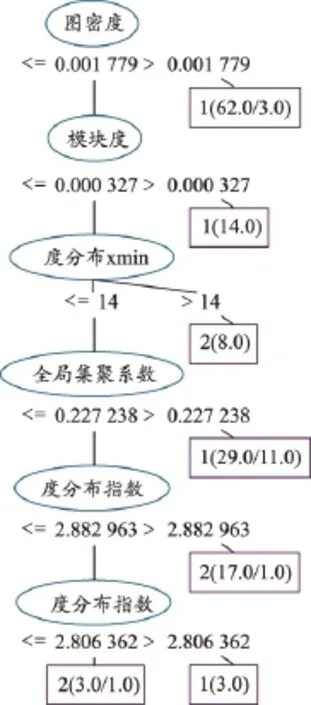
图8 年龄因素决策树模型

4 讨论

人体是一个动态复杂系统，体征时序数据网络化可以整体考察体征时序数据隐含的健康状态特征，发现和确认与健康状态高度关联的模式和规律。

本文的研究表明，网络图密度和健康状态具有较高的相关性，图密度表示网络中边的密集程度，时序数据的变动率是影响网络图密度的主要因素，变动率越高则时序数据中节点的可见性越高，图密度越大。健康的人体系统具有较好的适应能力，在生理体征时序数据上的体现为体征数据的变化较为缓慢，因此年龄、疾病等因素会使体征时序数据VG网络的图密度增加。

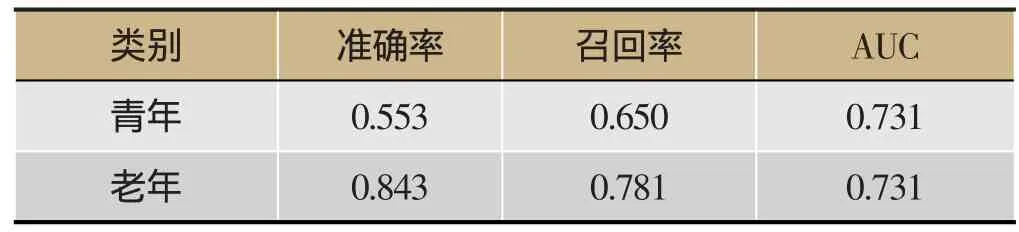
表4 年龄因素分类结果

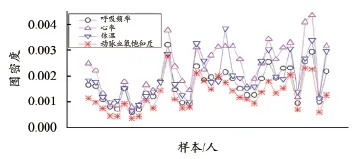
图9 各样本心率、呼吸频率、体温和动脉血氧饱和度时序数据VG网络的图密度

本研究中老年人体征数据的采集采用了穿戴设备，可穿戴设备作为一种新兴的技术，将其应用到医疗行业既是一个机遇也是一个挑战。可穿戴设备比传统医疗设备便捷，是解决老年人健康问题的有效手段，但当前的可穿戴设备在数据采集的可靠性和噪声处理适用性方面仍存在不足，需要在开放环境的适应性和关键技术研究方面得以提高，从而促进体征数据的高质量便携式采集。。

1 Lin W, Orgun M A, Williams G J. An overview of temporal data mining. In: Proceedings of the 1stAustralian Data Mining Workshop, 2002: 83-90.

2 贾澎涛,何华灿,刘丽,等.时间序列数据挖掘综述.计算机应用研究, 2007, 24(11): 15-18, 29.

3 Costa M, Goldberger A L, Peng C K. Multiscale entropy analysis of biological signals. Phys Rev E Stat Nonlin Soft Matter Phys, 2005, 71(2): 021906.

4 Costa M, Goldberger A L, Peng C K. Multiscale entropy analysis of complex physiologic time series. Phys Rev Lett, 2002, 89(6): 068102.

5 Lacasa L, Luque B, Ballesteros F, et al. From time series to complex networks: the visibility graph. Proc Natl Acad Sci U S A, 2008, 105(13): 4972-4975.

6 Milo R, Itzkovitz S, Kashtan N, et al. Super families of evolved and designed networks. Science, 2004, 303(5663): 1538-1542.

7 Nunez A, Lacasa L, Valero E, et al. Detecting series periodicity with horizontal visibility graphs. Int J Bifurcat Chaos, 2012. 22(7): 1250160. 8 Zhang J, Small M. Complex network from pseudoperiodic time series: topology versus dynamics. Phys Rev Lett, 2006, 96(23): 238701.

9 Iacovacci J, Lacasa L. Visibility graph motifs. ar Xiv preprint ar Xiv,2015, 1512: 00297

10 Newman M E J. The structure and function of complex networks. SIAM Rev, 2003, 45(2): 167-256.

11 Albert R, Barabási A L. Statistical mechanics of complex networks. Rev Mod Phys, 2002, 74(1): 47.

12 Quinlan J R. Induction of decision trees. Mach Learn, 1986, 1(1): 81-106.

13 Quinlan J R. Improved use of continuous attributes in C4.5. J Artif Intell Res, 1996: 77-90.

14 Goldberger A L, Amaral L A N, Glass L, et al. PhysioBank, PhysioToolkit, and PhysioNet: components of a new research resource for complex physiologic signals. Circulation, 2000, 101(23): e215-e220.

15 Csardi G, Nepusz T. The igraph software package for complex network research. Inter J Complex Sys, 2005, 1695(5): 1-9.

16 Clauset A, Shalizi C R, Newman M E J. Power-law distributions in empirical data. SIAM Rev, 2009, 51(4): 661-703.

Classification of Biological Signals Time Series by Extracting the Network Features Based on Visibility Graph

Jiao Xiaoyu1, Zhou Xuezhong1, Hu Jingqing2, Xie Qi3, Zhou Hongwei4
(1. College of Computer Science and Information Technology / Beijing Key Laboratory of Traffic Data Analysis and Mining, Beijing Jiaotong University, Beijing 100193, China;
2. Institute of Basic Theory, China Academy of Chinese Medical Sciences, Beijing 100700, China;
3. China Academy of Chinese Medical Sciences, Beijing 100700, China;
4. Traditional Chinese Medicine Data Center, China Academy of Chinese Medical Sciences, Beijing 100700, China)

This study aimed to transform the time series to network features using complex network approaches, and investigate associations between physiological network features and human health state. In this study, networks of standard heart rate time series and physiologic time series of the elderly that collected by wearable devices were built using visibility graph method. Then network features were extracted from these networks, and decision tree model was applied to analyze the main factors of network features contributing to heart disease and age. It was found that the fractal characteristic of heart rate time series brought out powerful law distribution for the degree distribution, and the network density became one of the major factors which were relevant to heart disease and age. In conclusion, it was indicated that topological features of networks underlay the dynamic characteristics of human physiologic time series. However, the correspondence between them still remained to be clarified.

Time series, complex network, network features, biological signals, elderly health

10.11842/wst.2016.04.018

R19

A

（责任编辑：朱黎婷，责任译审：朱黎婷）

2016-04-06

修回日期：2016-04-13

＊ 科学技术部国家科技支撑计划项目（2013BAH06F03）：服务老年公寓的健康服务应用系统研发与应用，负责人：谢琪；科学技术部国家中医药行业科研专项（201307003）：基于中医特色的老年社区的健康监测与干预关键技术研究，负责人：胡镜清。

＊＊ 通讯作者：周雪忠，本刊编委，教授，主要研究方向：复杂网络、数据仓库、数据挖掘。