Matlab在指数函数和对数函数学习中的应用
2016-03-19欧阳仁泽
欧阳仁泽
摘 要:在指数函数和对数函数的学习过程中,利用Matlab对指数函数和对数函数进行仿真,把难以理解的抽象概念用图象显示出来,能够变抽象思维为形象思维,有助于把握数学问题的本质,增强学习效果。本文介绍了Matlab程序和仿真结果。
关键词:Matlab;指数函数;对数函数
中图分类号:G633.6 文献标识码:A 收稿日期:2015-12-04
1. 指数函数
在Matlab上编程,绘制指数函数 y=ax(a>0,a≠1)的图象,程序如下:
for a=[1/5 1/4 1/3 1/2 2 3 4 5];
x=-30:0.1:30;
y=a.^x;
y1=0*x;
plot(x,y1,'m',y1,x,'m',x,y);
xlabel('x');
ylabel('y');
title(['指数函数y=a^x的图象']);
if a<1;
text(-1,(a)^(-1),['y=',num2str(a),'^x']);
else
text(1,(a)^1,['y=',num2str(a),'^x']);
end
text(-0.2,0.5,'(0,1)');
grid on
axis ([-3 3 -2 6]);
pause(1)
hold on
end
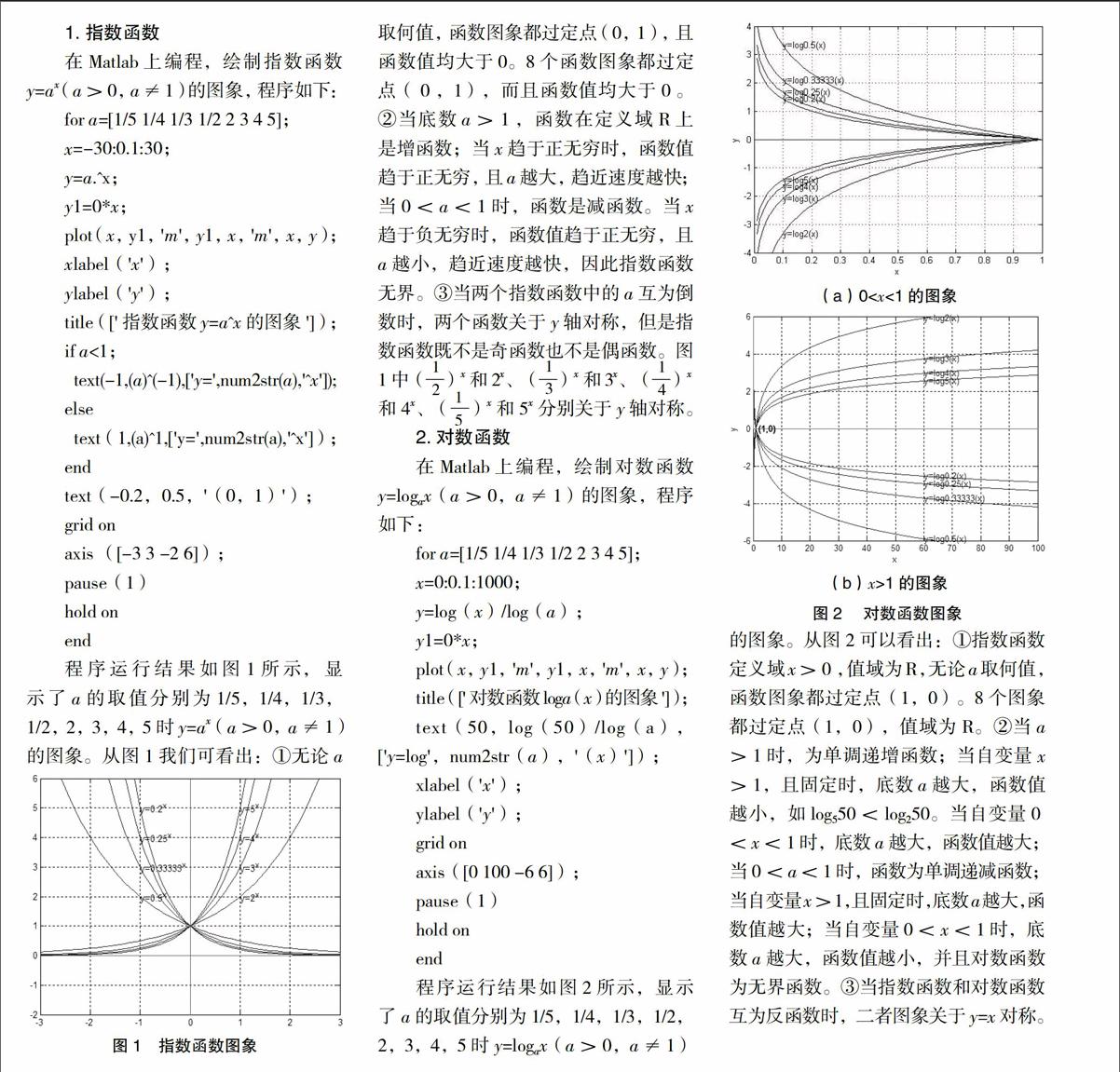
程序运行结果如图1所示,显示了a的取值分别为1/5,1/4,1/3, 1/2,2,3,4,5时y=ax(a>0,a≠1)的图象。从图1我们可看出:①无论a取何值,函数图象都过定点(0,1),且函数值均大于0。8个函数图象都过定点(0,1),而且函数值均大于0。②当底数a>1,函数在定义域R上是增函数;当x趋于正无穷时,函数值趋于正无穷,且a越大,趋近速度越快;当0 和4x、(—)x和5x分别关于y轴对称。 2.对数函数 在Matlab上编程,绘制对数函数 y=logax(a>0,a≠1)的图象,程序如下: for a=[1/5 1/4 1/3 1/2 2 3 4 5]; x=0:0.1:1000; y=log(x)/log(a); y1=0*x; plot(x,y1,'m',y1,x,'m',x,y); title(['对数函数loga(x)的图象']); text(50,log(50)/log(a), ['y=log',num2str(a),'(x)']); xlabel('x'); ylabel('y'); grid on axis([0 100 -6 6]); pause(1) hold on end 程序运行结果如图2所示,显示了a的取值分别为1/5,1/4,1/3,1/2, 2,3,4,5时y=logax(a>0,a≠1)的图象。从图2可以看出:①指数函数定义域x>0,值域为R,无论a取何值, 函数图象都过定点(1,0)。8个图象都过定点(1,0),值域为R。②当a>1时,为单调递增函数;当自变量x>1,且固定时,底数a越大,函数值越小,如log550
