外压检测装置密封胶芯偏心距优选有限元分析

徐新河

（长庆油田第六采油厂，陕西定边718606）



外压检测装置密封胶芯偏心距优选有限元分析

徐新河

（长庆油田第六采油厂，陕西定边718606）

摘要：以外压检测装置密封胶芯为研究对象，通过对防喷器闸板胶芯的密封原理研究，建立胶芯密封过程的非线性大变形有限元仿真模型，根据仿真结果，对密封胶芯的重要结构参数——偏心距进行优选。结果表明：偏心距越大，胶芯的等效应力越大，接触应力也越大，最大接触应力主要分布在胶芯的圆弧部分；偏心距越大，胶芯圆弧部分和平面部分的接触应力不均勾性增大；优选偏心距e 为0.5mm。

关键词：外压检测；密封胶芯；偏心距；优选

保证套管连接密封性能的关键是判定和检验套管连接是否合格。在下套管过程中，依次对套管连接部位进行气密封检测，才能直接验证密封的合格性，因此在线检测套管接连密封性方式开始被重视［1-3］。外压检测套管螺纹密封装置确保检测准确性的前提是环形密闭空间具有可靠的密封性，如果检测装置创造的环形密闭空间的密封性得不到保障，即环形密封空间本身就存在泄漏的可能性，后续对套管螺纹密封的检测也就无从谈起。因此，密封胶芯具有较好的密封性是装置设计中的关键技术。

1 外压检测胶芯密封原理

不同于闸板胶芯，外压检测密封胶芯分为正面密封面和背面密封面，密封面要满足一定的接触应力。正面密封面包括套管密封面、接箍密封面和胶芯平面密封面，背面密封面主要是胶芯背部与闸板之间的密封。不同接触面和同一接触面的不同部位在连续区域的接触应力都要大于内部检测压力，且应尽量分布均匀，不仅有利于提高密封可靠性，更能够提高胶芯的使用寿命。

设外压检测胶芯正面密封面和背面密封面连续密封区域的最小接触应力为pmin，内部检测气体压力为pq，为满足密封要求，有

式（1）是满足密封要求的基础，同时还应满足胶芯最大等效应力尽量小，保证胶芯不失效。另外，较优的密封结构应满足最大接触应力和最小接触应力的差值尽量小，以提高胶芯的寿命。

基于闸板防喷器的胶芯特点，结合需要满足的密封条件，设计的密封胶芯如图1所示，其中：区域A是密封套管的圆弧部分；区域B是密封接箍的圆弧部分；区域C是密封两胶芯间的平面部分；区域D是背面密封闹板圆弧部分；区域E是背面密封闸板平面部分。只有正面和背面密封区域的接触应力都达到要求时，才能实现胶芯的可靠密封。

图1　密封胶芯的结构

2 胶芯有限元模型的建立

本文采用ABAQUS/Standard求解器进行求解。本文涉及的密封接触属于大变形接触问题，存在材料的非线性、边界条件非线性以及几何非线性［4-5］。为使非线性接触问题的复杂性变得简单化，同时提高分析的效率，做以下假设：

1） 材料行为各向同性，忽略材料在制造过程中可能出现的不均匀性。

2） 密封接触之间存在固定的摩擦因数。

3） 密封胶芯是重点研究对象，模型关于平面对称，因此为减少计算量，提高模型收敛的可能性，建立1/2模型。

胶芯与套管接箍接触密封的有限元模型如图2所示，套管外径127mm（5英寸），壁厚为12.14mm，接箍外径141.3mm。由于仿真模拟中套管和接箍的连接不是重点研究对象，为简化模型减小计算量，不对套管和接箍的连接进行精确建模，因此将两者的连接模型简化为一个整体。

以胶芯结构的主要尺寸为基础，忽略次要因素影响，对模型做必要的简化，在不影响计算精度的情况下，提高模型的计算效率。橡胶和垫铁通过硫化工艺成型，可以简化一个整体，为减少接触对，便于分析收敛。橡胶和垫铁设置为一个部件，在建模过程中通过划分块区别出橡胶和垫铁。

图2　有限元模型

在建模过程中简化模型，忽略倒角等形状特征对划分网格的影响，对部件分块后，采用8节点六面体单元C3 D8 R H划分，并对橡胶大变形部位进行网格细化。网格划分采用扫掠网格划分技术，算法为M edialA xis算法，得到了质量较好的网格。套管接箍刚度大，网格尺寸设置较大。胶芯和套管的网格划分模型如图3所示。

图3　模型的网格划分

3 偏心距参数的优选

偏心距是整个结构中的重要尺寸参数，本文针对偏心距e＝0、0.5、1.0、1.5mm 4种情况，利用有限元仿真分析偏心距对密封性能的影响，优选出适合于外压检测密封胶芯的偏心距。偏心距为0、0.5、1.0、1.5mm 4种情况下的Mises应力云图如图4。

由图4可以看出：随着偏心距e的增加，胶芯的等效应力随之增加；最大等效应力的位置都在垫铁上，位于垫铁圆弧面和平面的交界处，这是由于胶芯在抱紧后挤胶量增加，在垫铁圆弧面和平面的交界处，垫铁同时承受着圆弧部分和平面部分橡胶的挤压，导致此处等效应力最大；橡胶的等效应力在垫铁圆弧面和平面的交界处以及圆弧部分相对较大，圆弧部分较大的等效应力分布在圆弧面上下部位，成2条带状分布。因此，对于密封胶芯，较大的偏心距增大了胶芯的变形受力，会影响胶芯的寿命。

图4　Mises应力云图

图5为不同偏心距情况下模型中胶芯表面的接触应力云图，接触应力是判断该密封件是否能实现密封的关键因素。

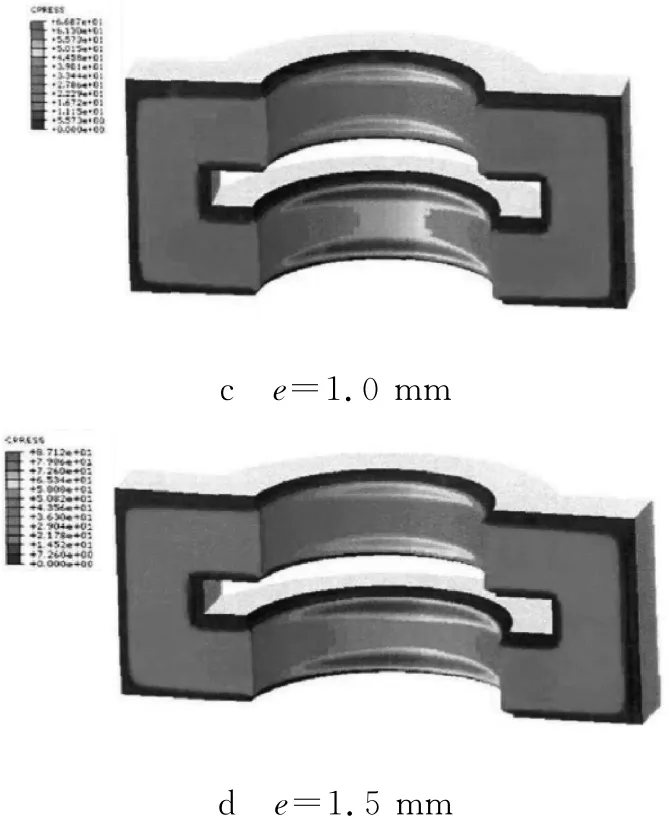
图5　不同偏心距下胶芯表面接触应力云图

由图5可以看出：在初步设计的尺寸参数下，不论有无偏心距，胶芯的最大接触应力都在圆弧面处；随着偏心距的增加，最大密封接触应力增加；偏心距每增加0.5mm，最大接触应力按20MPa的幅度增加；无偏心距时，圆弧部分的接触应力分布较为均匀，但是比平面部分接触应力大10MPa；存在偏心距时，圆弧部分的接触应力分布开始不均勾，最大接触应力主要位于圆弧面的上下边缘部分，上下呈梭形带状分布。

密封胶芯达到密封要求，需满足：

1） 连续区域接触面的最小接触应力等于或大于内部检测压力。

2） 接触应力分布连续且均匀。

3） 接触应力具有一定的接触面积。

由于模型是三维模型，为了更准确地分析不同偏心距下胶芯各部位径向和轴向的接触应力情况，按如图6所示的路径对胶芯密封面的接触应力情况做详细分析。图6为胶芯的1/2模型，密封套管路径1-1、1-2、1-3；密封接箍路径2-1、2-2、2-3；密封侧面轴向路径3-1。

图6　接触应力路径

4组不同偏心距下，胶芯密封套管圆弧面1-1处、1-2处的接触应力如图7所示，可以看出：随着偏心距的增加，密封套管1-1处和1-2处的接触应力都增大；同一偏心距下，1-1处的接触应力大于1-2处的接触应力；1-1处接触应力呈2个波峰状分布不均，1-2处接触应力分布较均匀。

1） 当e＝0mm时，1-1处和1-2处的接触应力都相对较小，最大接触应力20.8MPa出现在1-1处，最小接触应力8.3MPa位于1-2处，两者相差12.5MPa。圆弧部分的接触应力在轴向分布相对均匀。

2） 当e＝0.5mm时，最大接触应力为35MPa，最小接触应力为17MPa，两者相差18MPa，在1-1处开始出现2个波峰状态。

3） 当e＝1.0mm时，最大接触应力为54.5MPa，最小接触应力为19.3MPa，两者相差35.2MPa。

4） 当e＝1.5mm时，1-1处的最大接触应力陡增，特别是2个波峰处，最大接触应力达到70.1MPa，最小接触应力为27.8MPa，两者相差42.3MPa。

图7　胶芯密封套管圆弧面轴向接触应力分布

胶芯密封接箍圆弧2-1处、2-2处的接触应力分布如图8所示。密封接箍处的轴向应力分布趋势与密封套管处的趋势基本相同。偏心距增大，接触应力增大，最大接触应力均位于2-1处，最小应力位于2-2处。

1） 当e＝0mm时，2-1和2-2处的接触应力接触应力较小，最大和最小接触应力分别为24.7MPa和8.4MPa，两者相差16.3MPa。胶芯密封接箍圆弧面处接触应力分布相对均匀。

2） 当e＝0.5mm时，最大和最小接触应力分别为40.6MPa和15.0MPa，两者相差25.6MPa，圆弧面处接触应力分布开始出现不均匀性。尤其是2-1处，接触应力幵始出现2个波峰状。

3） 当e＝1.0mm时，接触应力显著提高，最大和最小接触应力为65.2MPa和19.2MPa，两者相差45.7MPa。

4） 当e＝1.5mm时，最大和最小接触应力为85.3MPa和21.6MPa，两者相差63.7MPa。

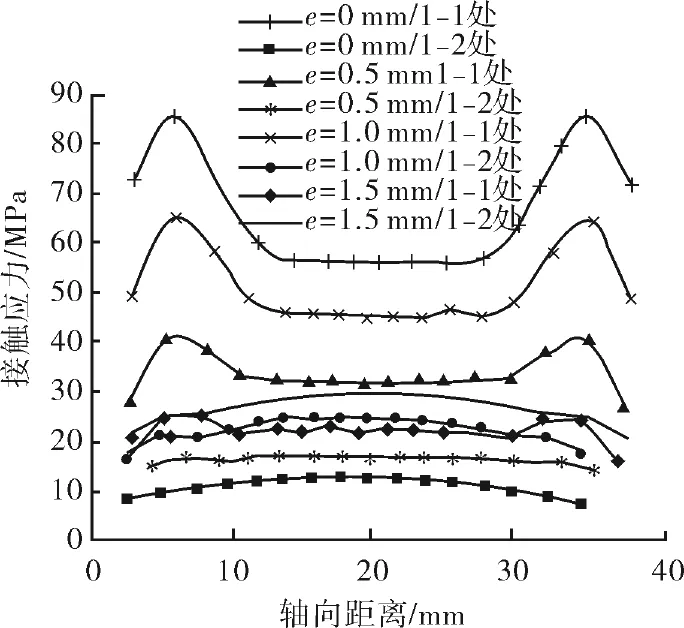
图8　胶芯密封接箍圆弧面轴向接触应力分布

对比图7～8可以看出：同一偏心距下，胶芯密封套管圆弧部分和接箍圆弧部分的轴向接触应力分布情况是相似的，胶芯密封接箍圆弧部分2-1处比密封套管圆弧部分1-1处的接触应力大，在1-2处和2-2处接触应力大小差别不大；随着偏心距的增大，胶芯密封套管圆弧部分和胶芯密封接箍圆弧部分的接触应力增大，最大接触应力和最小接触应力的差值增大，圆弧部分的不均匀性更显著。

路径1-3（2-3）处是考虑接触应力在圆弧部分周向和平面部分径向的整体分布趋势，胶芯密封套管圆弧和平面部分的整体接触应力如图9所示，分析可知：圆弧对称面处接触应力最大，接触应力沿着圆弧面成抛物线下降直至圆弧与平面交界处；圆弧部分和平面部分的交界处是整个路径中接触应力最小的部位；胶芯密封套管平面处的接触应力分布均匀；随着偏心距的增加，圆弧部分和平面部分的接触应力整体增加，偏心距越大，圆弧部分的接触应力曲线坡度越大，接触应力的不均匀性更加显著。

图9　胶芯密封套管圆弧和平面接触应力

胶芯密封接箍圆弧和平面部分的整体接触应力如图10所示，可以看出：偏心距越大，整体接触应力增大，圆弧部分的接触应力不均匀性显著，平面部分的接触应力分布较均匀。

图10　胶芯密封接箍圆弧和平面接触应力

轴向侧面的密封是胶芯密封套管和接箍在平面部分的连接部位，可能由于胶芯密封套管和接箍的变形不一致而导致接触应力分布不均。具体的接触应力情况如图11所示：同一偏心距下，轴向侧面的接触应力分布均匀，偏心距增大使得接触应力相对增大；在整个正面密封中，轴向侧面接触应力相对较小，与胶芯密封套管和接箍平面部分的接触应力相当。

综上所述，偏心距e＝0mm时接触应力分布均匀，但接触应力较小，且考虑到需要存在一定的偏心距可保证不出现密封胶芯半径差为0的情况，因此应该具有一定的偏心距。偏心距分别为1.0、1.5mm时，Mises应力较大，接触应力的分布不均匀性很显著，最大接触应力均超过了所需的接触应力，而最小接触应力却没有达到需求值。因此，选用e＝ 0.5mm作为胶芯的偏心距参数值。

图11　胶芯密封轴向侧面的接触应力

4 结论

1） 偏心距增加，胶芯密封面的接触应力整体增加，胶芯的Mises应力增大，较大的偏心距使胶芯的变形受力增大，对胶芯的寿命不利。

2） 同一偏心距下，密封圆弧部分的接触应力分布不均，平面部分和轴向侧面部分接触应力相对均匀。

3） 偏心距对接触应力分布的不均匀性有比较显著的影响，小偏心距下密封接触应力的分布较均匀，大偏心距下接触应力在圆弧部分增加幅度大，胶芯整体的接触应力分布不均匀性显著增加。

4） 优选e＝0.5mm作为胶芯的偏心距参数值。

参考文献：

［1］ 黎启柏，卢广权.气体泄漏检测方法及其工程应用［J］.机床与液压，2005，5（11）：130-131.

［2］ 刘浩.基于外压压差法高压气密性检测系统研究［D］.太原：太原科技大学，2014.

［3］ 卢飒.密封件气密性的智能检测方法研究［J］.仪器仪表装置，2003（5）：17-19.

［4］ 王露.轮毂轴承多工况疲劳寿命建模与数值仿真［D］.杭州：浙江工业大学，2009.

［5］ 杨晓翔.非线性橡胶材料的有限元方法［M］.北京：石油工业出版社，1999.

［6］ 周星.石油套管螺纹连接性能仿真分析［D］.东营：中国石油大学，2009.

试验研究

External Pressure Detection Device Packing Unit Offset Optimization of Finite Element Analysis

X U Xinhe
（No.6 Production Plɑnt，Chɑngqing Oilfield，Dingbiɑn 718606，Chinɑ）

Abstract：Pressure detection device outside packing unit for the study，through the blow out preventer seal plastic core principles，rubber core model of nonlinear finite element simulation was established for large deformation of the sealing process，according to the simulation results，the packing unit-an im portant structural parameters optimization of eccentricity. Results showed that greater eccentricity，equivalent stress the larger rubber core，bigger the contact stress，maximum contact stress distribution in circular part of the plastic core；eccentricity larger circular plastic core parts and flat parts of uneven contact stress increase；select the offset e＝0.5mm.

Key Words：pressure testing；packing unit；eccentricity；optimize

作者简介：徐新河（1977-），男，河北邢台人，工程师，主要从事采油机械、钻井设备及油田数字化设备的设计、制造工作。

收稿日期：2015-07-26

文章编号：1001-3482（2016）01-0051-05

中图分类号：T E931.1

文献标识码：A

doi：10.3969/j.issn.1001-3482.2016.01.012