基于MATLAB的曲柄摇杆机构优化设计

Optimization design of crank rocker structure under the given output angle constraint

李莹莹，游　敏，徐建军

LI Ying-ying, YOU Min, XU Jian-jun

（三峡大学 机械与动力学院，宜昌 443002）



基于MATLAB的曲柄摇杆机构优化设计

Optimization design of crank rocker structure under the given output angle constraint

李莹莹，游敏，徐建军

LI Ying-ying, YOU Min, XU Jian-jun

（三峡大学 机械与动力学院，宜昌 443002）

摘 要：在给定摇杆输出角约束的情况下，以曲柄摇杆机构的从动件运动角度与期望角度差值平方的和的最小值（即最小二乘法模式）为设计目标，建立单目标优化数学模型，通过MATLAB编程求解，研究了设计变量的个数和变量对象的选取对满足摇杆输出角约束的曲柄摇杆机构轨迹特性的影响，并确定了最佳的设计变量个数及变量对象的选取方案。

关键词：曲柄摇杆机构；优化设计；设计变量

0 引言

平面连杆机构结构简单，易于制造，能实现多种运动规律和运动轨迹，在工程实际中应用非常广泛[1]。然而，随着工业的不断发展，人们对曲柄连杆机构的运动特性、机构尺寸和杆件的受力情况等提出了更高的要求，使得连杆机构的设计难度也随之增大。连杆机构的设计问题通常可归为按给定的运动轨迹设计和按给定的运动规律设计[2]。对于这两类问题的求解，通常采用的是函数逼近法求解，该方法不仅计算复杂，而且变量较少时，计算精度也不高。若采用最优化方法对机构进行设计，可以大大简化[3]。

楼云江[4]等在给定摇杆最大摆角的情况下，借助于极位夹角和辅助角，建立了平均传动角最优化的曲柄摇杆机构优化模型，从而得到全局最大平均传动角，并确定相应的各杆杆长；苏有良[5]在给定行程速比系数、摆角、摇杆尺寸的设计条件下，建立了I、II型曲柄摇杆机构最小传动角与相对杆长的函数方程及其变化区间，解决了在此设计条件下曲柄摇杆机构不易获得最小传动角为最大值的最优传动性能解的设计问题；武丽梅[6]等通过仿真建立了杆长制造误差、运动副间隙与连杆曲线轨迹精度的数量级别关系。苏全卫、王晓侃[7]针对常用的滑块传动机构建立了速度和加速度的闭环矢量方程并借助MATLAB软件中的Simulink仿真工具对机构在仿真时间域内各个构件的瞬时位置、速度和加速度进行求解，提高了设计工作效率；马东辉、赵东[8]建立了三维实体结构优化设计的一般化数学模型，并采用MATLAB优化工具箱对模型求解，可以快速得出精确的优化结果。

本文通过对已知运动特性的曲柄摇杆机构的尺寸作优化设计，在已知运动特性的基础上，建立从动件运动角度与期望角度差值平方的和最小的单目标数学优化模型，并以经典的曲柄摇杆机构设计问题为算例，讨论了设计变量的个数及变量对象的选取对模型优化结果的影响。

1 问题提出

如图1所示，设计一曲柄摇杆机构，当曲柄由ϕ0转到ϕ0+90°时，摇杆的输出角实现给定的函数关系ψ=ψ(ϕ0)，且在该区间的运动过程中的最小传动角不得小于45°，即=45°。其中ϕ0和分别为对应于摇杆在右极限位置时曲柄和摇杆的位置角；ψ和ϕ是机架杆l4为原线逆时针度量的角度，分别为对应的摇杆转过一定的角度时摇杆和曲柄的输出角。

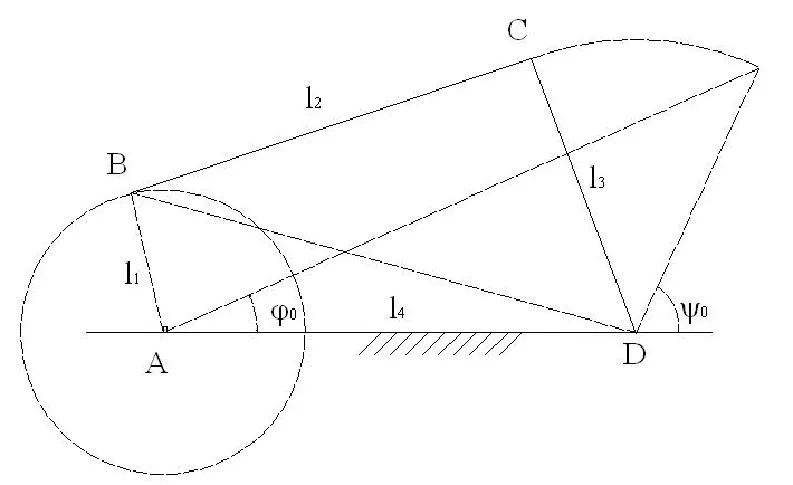
图1　曲柄摇杆机构简图

2 优化模型

2.1 设计变量

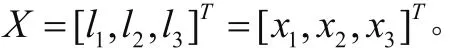
2.2 目标函数

实际的设计中，摇杆的输出角具有一定的轨迹，它会无限的趋近于某种函数曲线，要做到完全重合，其可能性基本为0，因此，我们仅能使所设计出来的曲柄摇杆机构的摇杆实际输出角尽可能的趋近于理论输出角。基于以上分析，我们取曲柄摇杆机构的已知运动规律与实际运动规律的偏差最小为指标来建立目标函数：

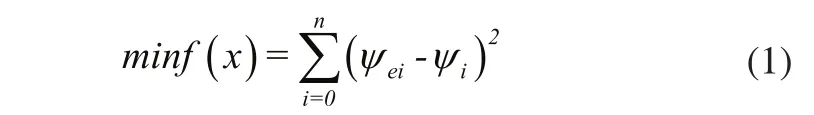
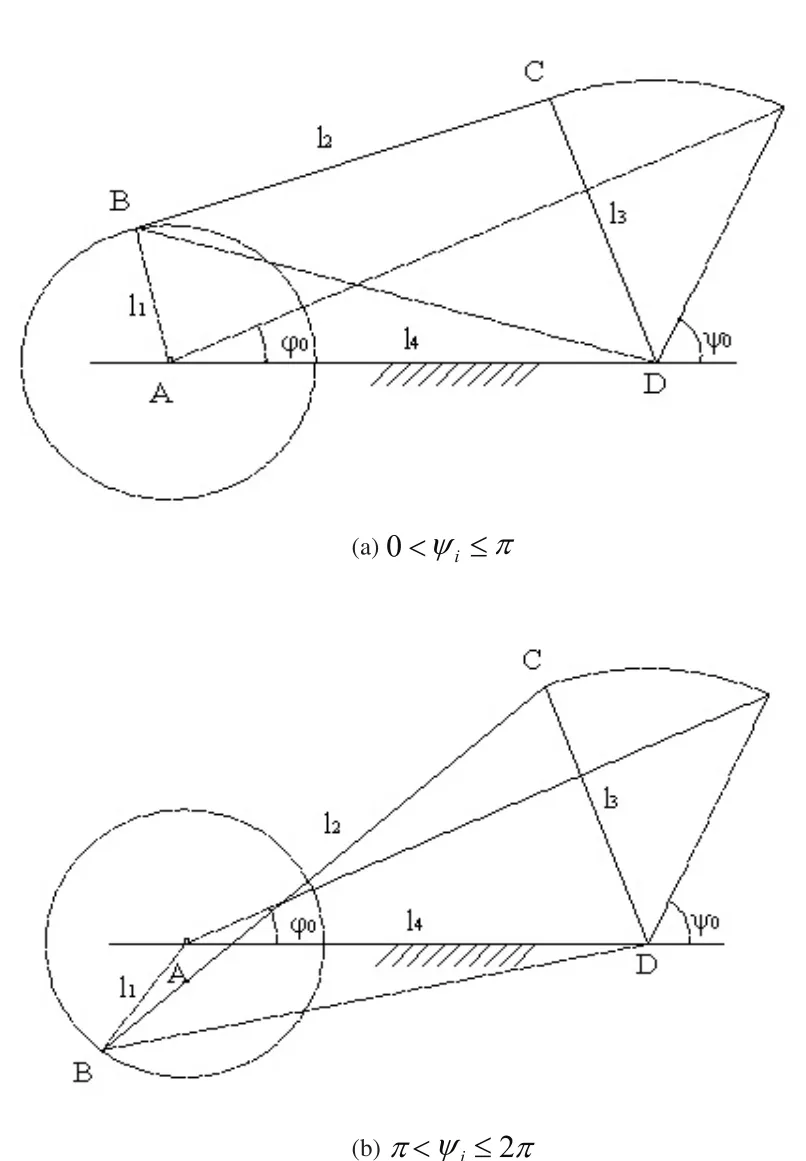
图2　曲柄摇杆机构摇杆的实际输出角

如图2所示，曲柄摇杆机构的实际输出角的表达式会随机构的转动而发生变化，当时，如图2(a)所示，；当时，如图2(b)所示，，即：

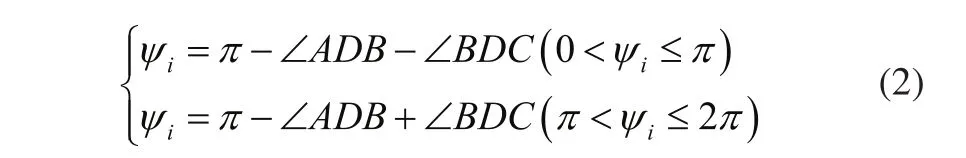
在本问题的研究中，由于初始角度ϕ0的取值范围无法确定，因此在编程求解的过程中要将两种情况都考虑其中，上述曲柄摇杆机构的实际输出角的表达式中，∠ADB 和∠BDC满足的关系式如下：

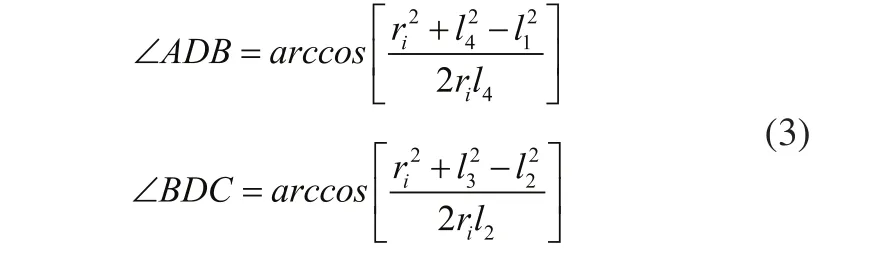
BD的长度用ri表示，根据余弦定理可以求得：

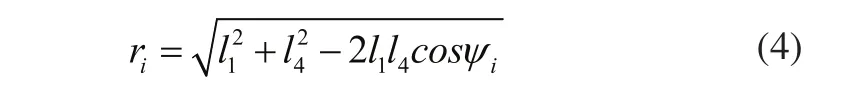
2.3 约束条件

曲柄摇杆机构受三方面的约束：一个是四杆机构中存在曲柄的条件，其次是曲柄摇杆机构的最小传动角约束条件，以及最后一个必须满足的边界条件。

1）四杆机构中存在曲柄的条件

由机械原理[1]可知，曲柄存在的条件：

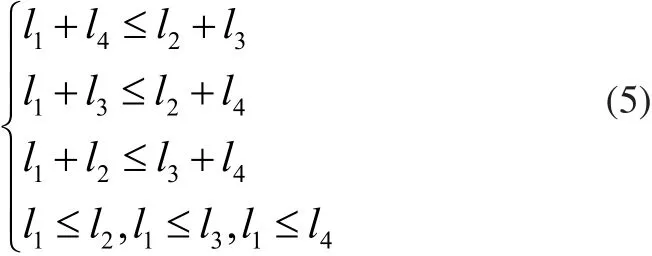
对应的约束函数为：

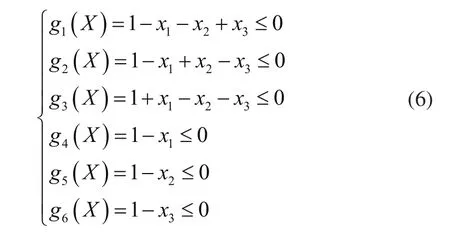
2）传动角约束条件

当机构运转时，其传动角的大小是变化的，为了保证机构传动良好，设计时通常应使≥40°[1]，该算例中要求机构在该区间运动过程中的最小传动角不得小于45°，即=45°。根据曲柄摇杆机构的传动特性可知，当曲柄和机架重合时传动角最小，因此传动角的约束条件为：

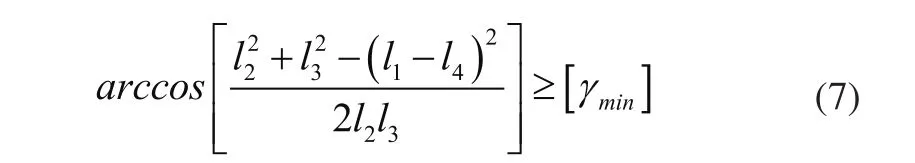
对应的约束函数为：

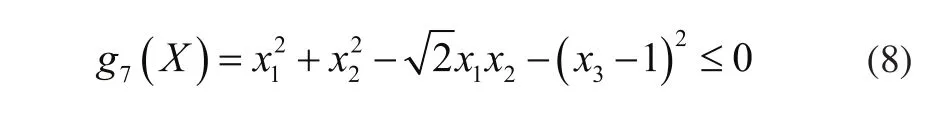
3）边界条件约束

对于机构的各个杆件尺寸，应保证其值为正数。

2.4 标准化模型

综上所述，将数学模型转化为标准形式如下：

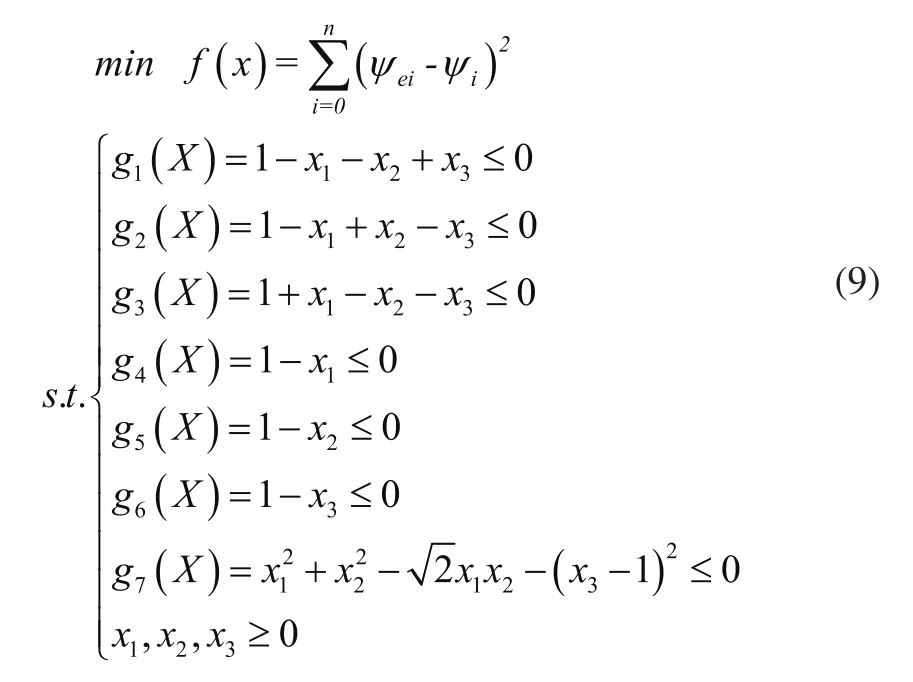
3 应用实例

3.1 三个设计变量的模型解

有学者在基于MATLAB的曲柄摇杆机构的优化设计中也研究了三个参数对模型求解的影响，规定各设计变量的最短杆与最长杆的比例设置在[1,10]的范围内，本文认为这种做法缺乏相应的理论依据，故在本文的研究中，没有限制最短杆与最长杆的比例。对于模型中设定x1,x2,x3三个变量的求解，利用所建立模型的线性约束条件和非线性约束条件确定目标函数的可行域，在可行域范围内选取适当的初始值，并利用计算软件MATLAB优化工具箱的Function()函数，对模型编程计算，通过在可行域范围内输入不同的初始值计算，我们得到的杆长设计结果如表1所示。

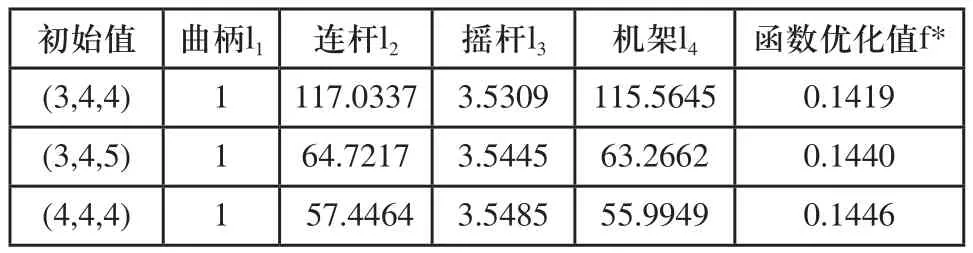
表1　三个设计变量的模型解

从表中的结果可以看出，通过选取可行域中不同的初始值，对三设计变量的曲柄摇杆优化结果会产生较大的影响，特别是当初始值取为（3,4,4）时，连杆和机架的长度几乎为初始值为（3,4,5）和（4,4,4）时的两倍，而摇杆的长度值几乎不受影响，函数的优化值极差为0.0027。

3.2 两个设计变量的模型解

本文中研究的主要是设计变量的个数对优化结果的影响，因此，在接下来的研究中，本文又讨论了2个设计变量时的优化情况。

当设计变量的个数为2时，根据机械原理四杆机构曲柄存在的条件可知：连架杆或机架是最短杆。文中以曲柄为最短杆进行讨论，设曲柄的长度为1，对于本文所给的算例，确定设计变量为2的研究中，大量的学者都对其进行计算求解并得出结论[9,10]，一般都是将曲柄和机架的长度设为1和5，没有考虑设计变量为摇杆和机架、连杆和机架的组合，也没有对初始确定的两杆取多组值进行深入研究，本文作者针对这一问题，对多种变量的组合全面考虑，每一组变量中设多组已确定杆长值组合，模型的求解结果如表2所示。

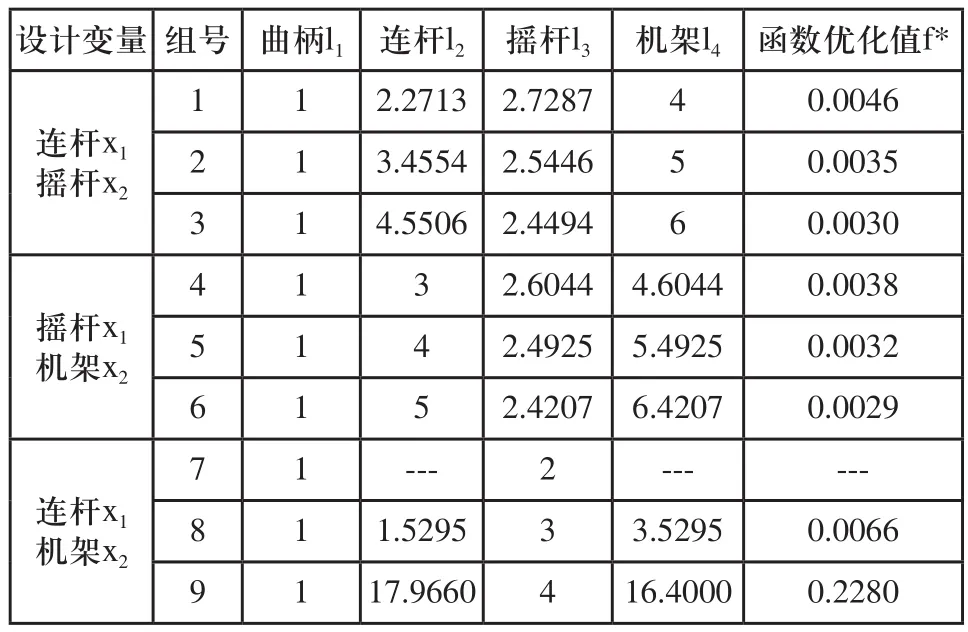
表2　两个设计变量的模型解

用MATLAB软件编程求解发现在初始值满足可行域的前提下，改变初始值取值，计算结果显示，模型的优化结果不受影响，因此，表2中没有列出初始值。曲柄和摇杆长度取为1和2时，程序无法正常运行出结果。确定曲柄长为1，机架长从4变化至5时，函数的优化值从0.0046降低至0.0030；确定曲柄长为1，连杆长从3增大至5时，函数的优化值从0.0038减小到0.0029；从总体情况来看，函数的优化值大部分在0.0029～0.0066之间，曲柄、连杆、摇杆和机架的长度分别取为1,5,2.4207和6.4207时，函数的优化值最小，为0.0029，结果最佳。曲柄和摇杆取值分别为1和4时，函数优化值明显较大，为0.2280。

4 结果分析

对于3设计变量的模型解，可以看出最短杆与最长杆的比例在1:117～1:57间大幅波动，初始值的选取对设计杆长连杆和机架的影响较大，将优化的杆长设计结果代入模型的约束条件，满足约束条件，表明该设计结果是可取的。改变使选取的不同的初始值，模型的目标函数值在0.1419～0.1446之间波动，最大值于最小值的极差达到0.0027，较之于两设计变量的目标函数值，偏差比较大。

从2设计变量的求解结果表中可以看出，不同于3设计变量的杆长设计值大幅波动情况，2设计变量求解的曲柄、连杆、摇杆和机架的长度比例维持在较稳定的水平，可行域范围内初始值的选取对模型的优化结果并无影响，目标函数的输出值基本在0.0029～0.0066范围内微小变化。当曲柄和摇杆取定值分别为1和4时，目标函数的输出值达到0.2280，相较于其他7组情况，偏差较大，曲柄和摇杆分别取1和2时，无法得到最终的杆长设计结果，观察其他7组的杆长设计结果，认为摇杆长度取2.4左右较佳。从表2中可以看出，当摇杆的取值偏差超过0.4，优化的结果便不太理想，连杆长在[3,5]，机架长在[4.5,6.5]区间内取值时，均能得到较理想的优化结果。

5 结论

本文主要研究平面四杆机构优化中，设计变量的个数及对象的选取对机构优化结果的影响，在模型的建立和求解中分别针对3个设计变量和2个设计变量的情况详细讨论，在设计变量为2个的模型求解中，取三组不同的设计变量组合进行优化求解，比较分析所得结果，得出以下结论：

1）平面四杆机构优化中，在可行域范围内选取初始值迭代计算，3设计变量的优化杆长输出值会随初始值选取的变化而发生较大波动，而两设计变量的杆长设计值不随初始值的变化而变化。

2）从优化的结果来看，2设计变量的优化结果明显优于3设计变量的优化结果，后者目标函数的输出值为前者的48倍左右。

3）综合以上分析，本文认为，在输出角约束条件给定的曲柄摇杆机构的最优化设计问题中，当确定摇杆和机架两个变量的长度时，能够得到最优的满足机构轨迹特性的解。

参考文献：

[1] 申永胜.机械原理教程[M].北京:清华大学出版社,1999.

[2] 杨世明,金国光.平面连杆机构平均传动角及其应用研究[J].机械,2008,35(8):19-22.

[3] 程友联,吴晓红.曲柄摇杆机构的参数设计法[J].机械设计,2010,27(9):60-62.

[4] 楼云江,邓雷.基于最佳平均传动角的曲柄摇杆机构设计[J].机械设计,2011,08:34-37.

[5] 苏有良.按最小传动角最大的曲柄摇杆机构优化设计[J].机械设计,2014,06:29-33.

[6] 武丽梅,耿华.基于ADAMS的曲柄摇杆机构的运动精度仿真研究[J].机械设计与制造,2006,10:9-11.

[7] 苏全卫,王晓侃.基于Simulink的曲柄滑块机构运动学建模与仿真[J].制造业自动化,2014,01:72-73+94.

[8] 马东辉,赵东.基于ANSYS和MATLAB的结构优化设计[J].制造业自动化,2013,19:106-108.

[9] 王文娟.基于MATLAB优化工具箱的平面连杆机构的设计[J].轻工机械,2006(4):76-79.

[10] 龚水明,詹晓刚.基于MATLAB优化工具箱的机械优化设计[J].制造业信息化,2008(10):92-94.

【上接第88页】

2）随着流量的增加，进气口与旋流管组件对空气流动的阻力会有增长，合理选择进气口、旋流管参数与数量能有效的减小空气流动压力损失。

3）通过分析提出了新的改进方案，数值模拟结果表明，改进方案在发动机负荷范围内粗滤器具有较好的流阻特性，在流量为1600m3/h时，压力损失降低了24.96%。

[1] 刘杰,王金香,吴秋红.沙漠空滤器原理及应用[J].农业装备与车辆工程,2006,(8):56-57.

[2] 贾彦龙,韩青,苏新梅,等.基于CFD的空气滤清器入口结构改进设计[J].湖北汽车工业学院学报.2007,21(4):9-12,21.

[3] 韩青,孙艺霞,贾彦龙,等.车用空气滤清器的流场数值模拟与结构设计[J].内燃机与动力装置,2007,(5):12-15.

[4] 陈海娥,李康,刘金玉,等.旋风除尘CFD分析[J].汽车技术,2003,(4): 13-16.

[5] 张惠,富旭光.空气滤清器的CFD分析及空气流动性优化[J].流体传动与控制,2011,(3):34-37.

[6] AI-Sarkhi, F. W. Chambers. Optimizaiton technique for design of Automotive air filter housings with improved dynamic performance and filtration[J].Particulate Science and Technology, 2004,(22):235-252.

[7] 王建文,汪华林,宋井伟.双进口双锥旋流管湍流流场的数值模拟[J].华东理工大学学报,2003,29(6):649-652.

[8] 李明华,王秉才,王建东.旋流管式车辆空气滤清器过滤技术研究[J].过滤与分离,2007,17(1):32-34.

[9] 霍玉荣.空气滤清器的设计与计算[J].内燃机与配件,2011,(7):9-16.

[10] 李佳,刘震涛,刘忠民,等.空气滤清器流动过程仿真与试验分析[J].浙江大学学报(工学版),2012,46(2):327-332.

作者简介：李莹莹（1992 -），女，湖北宜昌人，硕士研究生，研究方向为结构强度设计。

基金项目：湖北省自然科学基金项目：金属胶焊结构应力分布与失效机制研究（1214230）

收稿日期：2015-08-31

中图分类号：TH164

文献标识码：B

文章编号：1009-0134(2016)01-0102-04