飞轮储能系统径向永磁轴承力学性能和结构分析

2016-03-18Theanalysisofmechanicalperformanceandstructuralontheradialpermanentmagnetbearingsoftheflywheelenergystorage

制造业自动化 2016年1期

The analysis of mechanical performance and structural on the radial permanent magnet bearings of the flywheel energy storage

汤双清1,2，周东伟1,2，李庆东1，胡兰兰1

TANG Shuang-qing1,2, ZHOU Dong-wei1,2, LI Qing-dong1, HU Lan-lan1

（1.三峡大学机械与动力学院，宜昌 443002；2.三峡大学新能源微电网湖北省协同创新中心，宜昌 443002）

飞轮储能系统径向永磁轴承力学性能和结构分析

The analysis of mechanical performance and structural on the radial permanent magnet bearings of the flywheel energy storage

汤双清1,2，周东伟1,2，李庆东1，胡兰兰1

TANG Shuang-qing1,2, ZHOU Dong-wei1,2, LI Qing-dong1, HU Lan-lan1

（1.三峡大学机械与动力学院，宜昌 443002；2.三峡大学新能源微电网湖北省协同创新中心，宜昌 443002）

摘要：针对国家自然基金飞轮储能系统中径向永磁轴承的设计问题，根据轴承的拓扑结构讨论了轴承的类别。建立等效电流模型，推导出了轴承外圈永磁体轴线磁感应强度解析式，并结合有限元分析的结论推导出了轴承径向力的表达式。定义了径向力密度作为衡量轴承性能优劣的标准，并讨论了轴承结构参数对其性能的影响。对飞轮储能系统径向永磁轴承的设计有实际的指导意义。

关键词：拓扑结构；等效电流模型；径向力；径向力密度；结构参数

0 引言

最早的飞轮可以追溯到19世纪的瓦特蒸汽机时代，主要用来保持机器的平稳运转。随着科学技术的发展和科学工作者研究的不断深入，飞轮储能技术得到了长足的进步，作为一种使能技术目前已在包括航空航天、电动汽车和某些固定应用领域进入实践应用。综合来说，目前的飞轮储能系统主要用在两个方面：一是作为储能用的，如卫星和空间站的电源，车辆的动力装置，各种设备（计算机、医疗设备等）的不间断电源（UPS）：一是作为峰值动力要求用的，如分布式发电系统中电网电力的波动调节。磁悬浮轴承是飞轮储能系统重要的组成部分，其利用可控磁场提供无轴承支撑，使转子稳定悬浮于空间并且使转子和定子之间没有机械接触。永磁轴承具有工作可靠、转速高、无磨损、能好小等显著优点成为磁悬浮轴承研究的重点。在飞轮储能系统中如何优化设计永磁轴承的结构尺寸，以达到节省材料的目的非常重要。文献[1]分别用等效磁荷、等效电流理论推导了永磁体在空间的磁场分布解析表达式，并采用了Maxwell应力张量和虚功原理求出了磁力的解析式。文献[2]分别采用了静磁路法、等效磁荷发、动态磁路法对径向永磁轴承的承载力和刚度推导出了解析式，并对三种方法的优劣进行了对比分析。文献[3～6]也分别推导了径向永磁轴承的承载力和刚度的解析式，并分析了轴承结构尺寸对其性能的影响，对结构提出了优化。

本文采用分子电流学说的理论和有限元方法推导出了飞轮储能系统中径向永磁轴承径向力的近似解析表达式，并分析了轴承结构尺寸对其力学性能的影响。

1 永磁轴承的拓扑结构分析

永磁轴承是由两个按一定方向充磁的永磁体组合而成的，根据两个永磁体充磁方向和位置的不同而产生作用力的类型可分为吸力轴承、斥力轴承和向心轴承。图1永磁轴承永磁体拓扑结构图表示了空间中永磁轴承两个永磁体磁化方向和位置之间的关系。J1，J2表示永磁体磁化方向，β1，β2表示永磁体磁化方向与水平方向的夹角，θ表示永磁轴承的两个永磁体截面中心连线与水平方向的夹角。

图1 永磁轴承永磁体拓扑结构图

图2 永磁轴承永磁体相对位置图

表1　永磁体磁化方向的组合表

表2　=0时永磁轴承类别情况表

序号　1　 2　 3　 4　 5　 6　 7　 8类别　径吸　向心　径斥　向心　向心　径斥　向心径吸序号　9　 10　 11　 12　 13　 14　 15　 16类别　径斥　向心　径吸　向心　向心　径吸　向心径斥

表3　时永磁轴承类别情况表

2 径向永磁轴承的磁力计算

2.1 磁感应强度的计算

径向永磁轴承是飞轮储能系统的重要组成部分，主要用来承载转子的径向载荷，使转子悬浮于空间，避免机械接触。永磁轴承中永磁体的磁化方向对轴承的承载力和刚度不产生影响，故选择图2(a)所示结构的径向永磁轴承作为分析对象是可以的。图3所示为径向永磁轴承在空间中的位置和径向永磁轴承的结构尺寸。P(x0,y0,z0)，Q(x,y,z)分别为径向永磁轴承外内圈永磁体上的任意一点。

图3　永磁轴承空间位置图

文献[1]根据等效电流模型，结合毕奥—萨伐尔定律，推导出了永磁体周围介质的磁感应强度公式：

式中：B表示磁感应强度；

μ0表示真空磁导率；

Jm表示永磁体的体电流密度；

Jms表示永磁体的面电流密度；

R表示源点到场点的矢径，R表示源点到场点的距离；

V表示永磁体的体积，S表示永磁体边界面。

在均匀磁化的磁体内部，圆电流相互抵消，使得Jm=0。但是在永磁体边界上不能抵消，存在面电流Jms。其面电流密度与磁化强度的关系：

式中：

M表示永磁体的磁化强度；

n表示磁体边界的外法向单位矢量。

综合上述分析，式(1)可表示为：

在所研究的飞轮储能系统中，径向永磁轴承的外圈永磁体是过盈配合装配在真空容器上的，转子轴和轴承内圈永磁体配合装配在一起。根据牛顿第三定律，物体的作用是相互的。径向永磁轴承内外圈的永磁体将受到大小相等，方向相反的作用力。考虑到外圈永磁体是固定的，本文主要研究内圈永磁体在外圈永磁体产生的磁场空间中受到的径向磁力。

根据等效电流模型，外圈永磁体产生的磁场可以看成是其圆柱面1和2分别产生的磁场的矢量叠加。即：

结合式(3)，圆柱表面1的磁感应强度：

根据式(7)可推导出圆柱面1沿z轴方向，即P点坐标为(0,0,z)时，磁感应强度的表达式为：

同理，可以推导出圆柱面2沿z轴方向上的磁感应强度解析式可表示为：

所以，径向永磁轴承外圈永磁体在z轴方向上产生的磁感应强度表示为：

2.2 轴承磁力的计算

根据分子电流学说，均匀充磁的永磁体的磁场可以看成是分布在圆周表面的分子电流产生的。故可以将内圈永磁体的面电流看成是无数圈沿圆周方向的电流组合而成。而外圈永磁体对内圈永磁体的磁力求解，可转化成圆环导电线圈在点磁荷在空间产生的磁场中所受到的磁力的求解。空间中导线受到的磁力计算公式为：

式中：f表示导线受到的磁力；

L表示载流导线的长度；

I表示载流导线中的电流大小。

径向永磁轴承的永磁体1在空间产生的磁感应强度可分解成在xoy平面内的分量Br和沿z轴的分量B'z。则根据式(11)可知，分量Br对导线产生的磁力为径向永磁轴承的轴向力，分量B'z对导线产生的磁力为径向永磁轴承的径向力。故永磁轴承径向力可表示为：

在xoy平面或者平行于xoy平面的任意一点位置，轴承永磁体1在该点产生的磁感应强度在z方向的分量B'z可能是不相同的，但在同一圆周上的磁感应强度的大小是相等的。故轴承永磁体的圆柱表面3上的磁感应强度大小是相等的，同理圆柱表面4上的磁感应强度大小也是相等的。

图4所示为通过ANSYS软件，对结构尺寸为，R1= 2 0 m m，R2= 1 0 m m，h = 8 m m物理参数为Hc=400KA/m,Br=540mT,μr=1.18的圆环形永磁体求解得出的磁感应强度沿x轴方向分布图。通过此图可知，x轴方向（即径向方向）在原点出的磁感应强度是最小的，故用原点处的磁感应强度代表圆柱表面3和4上的磁感应强度上来计算3、4表面上的磁力是满足要求的。式(12)可表示成：

图4　圆环形永磁体x轴磁感应强度分布图

对永磁轴承内圈永磁体的圆柱表面3，设环路内电流强度为I3，则在与平面xoy平行的任一平面上的面电流Jms和电流I3的关系为：

根据安培定律，圆柱表面3某点处的电流元I.dl受到磁场的径向作用力为：

γ为电流元对应的圆心角。

所以，圆柱面3任一横截面（平行于xoy平面）的圆环载流导线受到的径向力为：

联合式(14)，对式(17)积分可得：

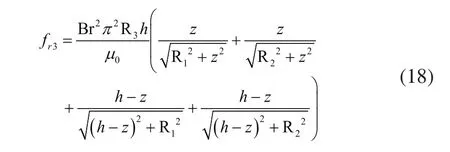
同理，可以求出内圈永磁体圆柱面4任一横截面（平行于xoy平面）的圆环载流导线受到的径向力为：

所以，径向永磁轴承内圈永磁体任一横截面受到的径向力为：

假若径向永磁体内圈在轴向产生λ的轴向位移，则可求出此时径向永磁轴承的径向力：

故当径向永磁轴承的内外圈处于初始位置，即λ=0 =0时，根据式(21)求出径向永磁轴承的径向力计算式为：

3 径向永磁轴承结构分析

对于给定要求的径向永磁轴承在满足径向力要求的前提下，应该使所用的永磁材料的体积最小，以达到节约材料和减小成本。特别是在飞轮储能系统中，由于技术的限制飞轮储能系统的小型化较难实现或者是实现后成本很大，故减少轴承材料的使用是非常有必要的。定义径向力密度作为衡量径向永磁轴承性能优劣的标准。径向力密度指径向永磁轴承的径向力与轴承体积的比值，记做χ，即：

根据式(23)可知，在实际的永磁轴承的设计时，满足设计要求的前提下应使x的值越大越好。x的值越大说明永磁来料的利用率越大。假设径向永磁轴承的内外圈永磁体的相对位移为零，选定永磁体的物理参数为Hc=400kA/m，Br=540mT，μr=1.18。图5表示结构参数R2=30，R3=20，R4=10，h=10时，径向力密度与圆柱半径R1的关系。图6表示结构参数R1=40，R3=20，R4=10，h=10时，径向力密度与圆柱半径R2的关系。图7表示结构参数R1=40，R2=30，R4=10，h=10时，径向力密度与圆柱半径R3的关系。图8表示结构参数R1=40，R2=30，R4=40，h=10时，径向力密度与圆柱半径R4的关系。图6表示结构参数R1=40，R2=30，R3=20，R4=10时，径向力密度与圆柱半径h的关系。

图5　R1与径向力密度关系图

图6　R2与径向力密度关系图

图7　R3与径向力密度关

图8　R4与径向力密度关系图

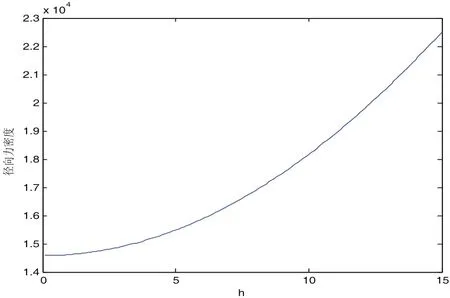
图9　h与径向力密度关系图

根据图5可知，R1的值越大径向力密度也增大。但当R1的值增大到某一值时，径向力密度的基本不变。若在增大R1的值，径向力密度会减小。根据图6可知，R2的值越大径向力密度越小，当R2达到某一值时径向力密度的减小得越快。根据图7可知，径向力密度的值随R3的增大而减小，而且两者之间有较好的线性关系。根据图7可知，径向力密度的值随R4的增大而增大，当R4增大到某值后径向力密度增大得越快。由图9可知，永磁轴承的轴向尺寸越大径向力密度的值越大。