贯穿式超精研圆锥滚子的研磨特性分析

The polish properties analysis of through-feed superfinishing tapered roller

薛进学，贾松阳，杨柏松

XUE Jin-xue, JIA Song-yang, YANG Bai-song

（河南科技大学 机电工程学院，洛阳 471003）



贯穿式超精研圆锥滚子的研磨特性分析

The polish properties analysis of through-feed superfinishing tapered roller

薛进学，贾松阳，杨柏松

XUE Jin-xue, JIA Song-yang, YANG Bai-song

（河南科技大学 机电工程学院，洛阳 471003）

摘 要：对贯穿式超精研工艺中圆锥滚子的研磨接触状态进行了分析。得到滚子表面的近似接触形状；接触中线的滚子素线上的应力大于周边滚子素线上的应力；单条滚子素线上的应力从滚子小端到大端呈逐渐增大趋势。基于材料去除率的经典Preston方程，推导出滚子研磨深度的计算方程并分析了其相关参数。存在最佳油石接触弧形半径，使滚子素线中端的研磨深度小于两端，有利于形成凸度。

关键词：圆锥滚子；超精研；Preston方程；材料去除量

0 引言

圆锥滚子是滚动轴承中的关键零件，滚子的加工质量对轴承的使用寿命有很大影响。超精研是加工圆锥滚子的最后一道工序，能在几秒至几十秒内，把工件的表面粗糙度由Rα0.63～0.16μm改善到Rα0.08～0.01μm，并能有效地去除磨削产生的振痕、波纹、螺旋线等缺陷以及极易磨损的凸峰和变质层等,装配而成的轴承噪声值明显下降，旋转精度、产品质量及寿命可靠性均有较大幅度的提高[1]。定姿态贯穿式超精研是滚子超精研加工的主要方式[2]。其原理如图1所示，被加工圆锥滚子依靠左右两个螺旋导辊的支撑和摩擦驱动作用自转和向前贯穿，位于正上方的油石前后往复振动，并以一定压力压向滚子，实现对滚子表面的加工。

图1　圆锥滚子定姿态贯穿式超精研原理简图

由于国内超精研加工技术起步较晚，目前，我国的总体技术水平要远远落后西方发达国家[3]。超精研的工艺参数大多基于生产实践，理论研究多集中在滚子凸度形成机理和导辊型面曲线的分析。因此对超精研研磨特性进行理论分析，有助于提高滚子的加工质量，能对生产实践起到指导作用。

1 滚子研磨接触状态

圆锥滚子在超精研过程中，油石的研磨作用形成了其表面质量和凸度。滚子在向前贯穿时（一般小端在前），由于滚子的锥形表面，其大小端与油石的接触状态显然是不同的。

图2　油石-滚子接触面积分析简图

滚子在加工过程中不断贯穿前进，其与油石的接触位置可以分为三个阶段，如图2所示。第一阶段是油石与滚子刚开始接触，第二阶段是油石与滚子完全接触，第三阶段是油石离开滚子。三个阶段油石和滚子的接触面积是在不断变化的。一般油石长度大于滚子长度，由于滚子贯穿速度很快，与开始接触和逐渐离开阶段相比，完全接触的时间要稍长一点，其接触面积也相对稳定。本文仅分析完全接触情况。

在油石和滚子的接触过程中，油石接触面为一弧面，如图3中网格线所示，其半径最小应与滚子大端半径相等。

图3　油石接触弧面示意图

由于圆锥滚子各处半径不同，不能直接用赫兹接触计算其接触弧长和应力分布。利用离散化思想，如图4所示，将滚子沿轴向离散化，在总长L内分n等份，每单元长Li，对应半径为r。每个离散单元可以近似看做圆柱体和凹形圆柱面的接触（图5），可计算出接触弧长b和最大应力。

图4　滚子离散化示意图

图5　离散单元接触分析简图

单元接触半弧长：

F压为油石对滚子的压力，L为滚子总长，μ1为油石泊松比，μ2为滚子泊松比，E1为油石弹性模量，E2为滚子弹性模量。

从弧长方程中可以看到，不管其他参数如何变化，ri越大，接触弧长bi越大，即滚子从小端到大端的接触弧长应逐渐增大。取示例数据（滚子半锥角为2°，大端5mm，长度14mm）计算，可得到圆锥滚子的接触形状如图6所示，其接触是不规则的 “几”字形。

图6　圆锥滚子接触形状

由赫兹理论得最大接触应力：

滚子最大接触应力在接触单元的中线上，向两边逐渐减小。如图7所示。

图7　离散单元接触分析简图

接触单元的应力分布：

滚子每个接触单元的最大应力分布在接触中线上，那么在整个接触面，接触中心滚子素线上的应力值应该整体大于其周边素线上的应力值。也就是说，超精研滚子在自转运动时，其某一素线从与油石接触开始，其应力值从零逐渐增大，到接触中间位置达到最大，然后减小到零，离开与油石的接触。

另外，在同一素线上，接触应力也是不同的。图8是接触中线上最大应力的分布图。

图8　中线最大接触应力分布图

由图可知，当圆锥滚子上某素线转到接触中线位置时，该素线上的应力分布从小端到大端逐渐增大。图中滚子在靠近大端处，应力突然以较大幅度增加。这主要是应力方程中油石的弧形半径取的是滚子的大端半径，使应力值在接近大端时趋近无穷大。实际加工过程中，油石是逐渐磨损的，可知磨损到其弧形半径接近滚子大端半径时，将使滚子大端承受较大应力。

应力值的分布并不表示滚子实际的研磨量趋势。在实际研磨过程中，圆锥滚子之所以能够形成凸度，其中端研磨量必定是少于大小两端的。研磨量是研磨深度和接触面积综合的结果。

2 建立滚子研磨深度方程

Preston方程是经典的材料去除率方法，在多个领域得到应用，已被大量实践验证了其合理性[4]。其表达式如下：

将式(4)改写为单位弧长的材料去除率的研磨方程，已知滚子自转速度：

改写Preston方程如下：

则得到基于弧长的Preston方程：

以上建立了基于弧长的材料去除率Preston方程，材料去除率与单位弧长的比值实际上就是研磨深度。

方程中滚子应力分布已做过分析。在超精研过程中，直接影响工件材料磨除的运动有油石的往复直线运动和工件的旋转运动[6]。油石和滚子的相对运动速度如图9所示。

图9　油石-滚子运动分析简图

油石滚子相对速度：

v1为滚子自转线速度，v2为滚子贯穿速度，v3为油石速度（单位都为mm/s）。

分别确定方程中个速度参数。导辊旋转摩擦驱动滚子自转，滚子自转线速度为：

ω1为滚子自转角速度(rad/s)，r中为滚子中径(mm)，ω2为导辊自转角速度(rad/s)，R中为导辊中径(mm)，k为滑动系数，r为滚子半径(mm)。

滚子的贯穿速度与导辊的螺旋运动有关，线速度表达式为：

ω2为导辊自转角速度(rad/s)，h为导辊挡边螺旋导程(mm)。

油石在滚子表面作往复振动（频率为f，振幅为A），其振动方程为。油石的速度为：

综上，可得油石与滚子的相对切削速度为：

将式(1)、式(3)、式(7)、式(8)代入研磨深度方程式(6)，得到各接触单元的研磨深度为：

滚子超精研过程中，在整个接触区域内接触线上的应力最大，即当x=0时，接触线上的研深最大。

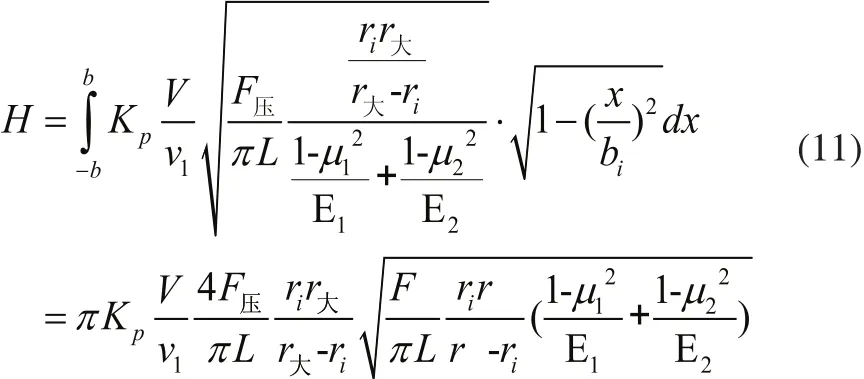
3 滚子研磨深度分析

在实际生产中，合理的超精加工过程一般分为粗超和精超2个阶段，粗超阶段采用较低的工件转速，较高的油石摆动频率和较大的油石压力，以达到理想的生产效率；精超阶段采用较高的工件转速，较低的摆动频率和较小的油石压力，以达到理想的表面粗糙度要求[7]。这与研磨深度方程得到的结果是一样的，越高的工件转速，越低的摆动频率和越小的油石压力使研磨深度越小。

另外，滚子素线上的研磨深度对圆锥滚子的凸度有直接的影响。随着圆锥滚子半径的变化，应使滚子素线上中部的研磨深度小于大小两端。分析研深方程中滚子半径的系数，有关的系数为滚子自转速度ω1和油石弧形半径R。取最大接触应力的滚子素线，固定油石半径R，ω1分别取为20mm/s，10mm/s，5mm/s得到图10的研磨深度趋势图和固定自转速度ω1，油石弧形半径R分别取5mm，10mm，20mm得到图11研磨深度趋势图。

图10　滚子自转速度对滚子研磨深度影响趋势图

图11　油石弧形半径对滚子研磨深度影响趋势图

对比图10和图11，可以看到油石弧形半径对研深存在较大影响。弧形半径较大时，沿滚子半径，研深逐渐减小（图11下图所示）；弧形半径减小到一定值后，滚子中端比两端的研磨深度小（图11中图所示），这显然是最理想的情况，有利于滚子素线凸度的形成。油石弧形半径继续减小时，研深又逐渐增大（图11上图所示）。由此可见，油石弧形对超精滚子凸度有很大影响。在研磨过程中，油石是不断磨损的，其弧形很难控制，需要更深入的研究。

4 结论

分析了定姿态贯穿式超精研过程中圆锥滚子的研磨接触形状和接触应力分布；在油石与滚子完全接触状态下，滚子上接触形状呈“几”字形；接触中线处的滚子素线上的应力整体大于周边素线；滚子单一素线上的应力值随滚子半径增大逐渐增大。

基于Preston方程，推导了圆锥滚子研磨深度方程。越高的工件转速，越低的油石摆动频率和越小的油石压力使研磨深度越小。与实际情况也是相符的。

存在最佳油石弧形，使滚子研磨深度中端少于大小端，有利于滚子素线形成凸度。油石弧形的影响还需进一步研究。

超精圆锥滚子的接触状态十分复杂，表面凸度形成机理也一直是研究的重难点。本文研究是在理想的假设前提下，Preston研深系数也需要实验求得，滚子的研磨特性还需继续深入研究。

参考文献：

[1] 周俊荣,刘明,贺宇,等.球面滚子外径超精机[J].轴承,2014,(8): 23-24.

[2] 高作斌,李庆玲.滚动轴承超精研工艺的特殊性[J].轴承, 2014,(8):53-58.

[3] 陈世友.圆锥滚子导辊设计与加工研究[D].洛阳:河南科技大学,2013:1-5.

[4] 吴昌林,王韦,李强,等.基于Preston方程的不锈钢曲面抛磨工艺参数分析[J].机械制造与自动化,2012,41(04):102-105.

[5] 樊成.光学曲面确定性抛光的面型精度控制研究[D].吉林:吉林大学,2014:30-31.

[6] 袁俊哲.精密和超精密加工技术[M].北京:机械工业出版社,2012.

[7] 郑红威,贺红霞,何萌,等.D42218N3W圆柱滚子超精加工工艺参数的确定[J].轴承,2014,(10):16-18.

【上接第29页】

比较图2和图4可以看出，FFMPC算法减少了太阳辐射对系统输出跟踪误差，应用MPC的MSE为1.38361844，应用FFMPC得到的MSE为0.2974895。从图6可以看出利用FFMPC算法控制效果优于MPC。

4 结论

基于前馈补偿和模型预测控制的复合控制器应用到太阳能集热系统的控制中效果明显优于MPC的控制效果，利用前馈控制减少了可测的随机大信号对输出的干扰，模型预测控制对随机系统具有很好的鲁棒性，应用仿真试验了FFMPC算法应用到线性菲涅尔集热场的控制中提高了系统的跟踪精度，控制量的变化量小，稳定性更好。

[1] 杜春旭.线性菲涅耳太阳能聚光系统的理论分析与实验研究[D].北京:北京工业大学,2013.

[2] G.A. Andrade, D.J. Pagano, J.D. Álvarez, M. Berenguel. A practical NMPC with robustness of stability applied to distributed solar power plants[J].Solar Energy,2013,92(7)106-122.

[3] Torrico, B. C., Roca, L., Normey-Rico, J. E., Guzman, J. L., Yebra, L. Robust nonlinear predictive control applied to a solar collector field in a solar desalination plant[J].Control Systems Technology , IEEE Transactions on,2010,18(6),1430-1439.

[4] A.J.Gallego,E.F.Camacho.Adaptative state-space model predictive control of a parabolic-trough field[J].Control Engineering Practice, 2012,20(9),904-911.

[5] Gil, P., Henriques, J., Cardoso, A., Carvalho, P., Dourado, A. Affine neural network-based predictive control applied to a distributed solar collector field[J].Control Systems Technology 2014;22:585-596.

[6] Cirre, C.M.,Valenzuela, L., Berenguel, M.,Camacho, E.F.. Feedback linearization control for a distributed solar collector field[J].Control Engineering Practice,2007,15(12),1533-1544.

[7] Carmona, R.. Analysis, Modeling and Control of a Distributed Solar Collector Field with a One-Axis Tracking System[D]. Spanish: University of Seville,Spain,1985.

[8] 关守平.计算机控制理论及应用[M].机械工业出版社,2012.

[9] 郭振凯,宋召青,毛剑琴.基于最小二乘支持向量机的非线性广义预测控制[J].控制与决策.2009,24(4):520-525.

[10] 郭健.一类非线性系统广义预测控制研究[D].南京:南京理工大学,2002.

作者简介：薛进学（1965 -），男，副教授，博士，研究方向为硬脆材料精密加工与检测、特种加工（超声振动加工）和制造系统工程。

收稿日期：2015-08-12

中图分类号：TG580.68；TH161+.14

文献标识码：B

文章编号：1009-0134(2016)01-0033-04