由一道物理题引发的对绳子张力的讨论
2016-03-17梁依斌
梁依斌
摘 要: 文献及很多大学物理教材和解题指导书的《刚体的定轴转动》一章都出现了一道关于绳子张力的习题。这些题中对绳子张力的分析都是错误的,有些教材甚至给出滑轮与绳子之间的摩擦力忽略不计的条件,这显然也是错误的,给学生造成误导。学生对“同一根绳上的张力处处相等”的结论印象深刻,这种知识负迁移影响令学生对绳子张力问题更费解。本文指出了教材和参考书对本题叙述和分析的疏漏,并对绳子张力进行了讨论。
关键词: 刚体 绳子张力 知识迁移
1.引言
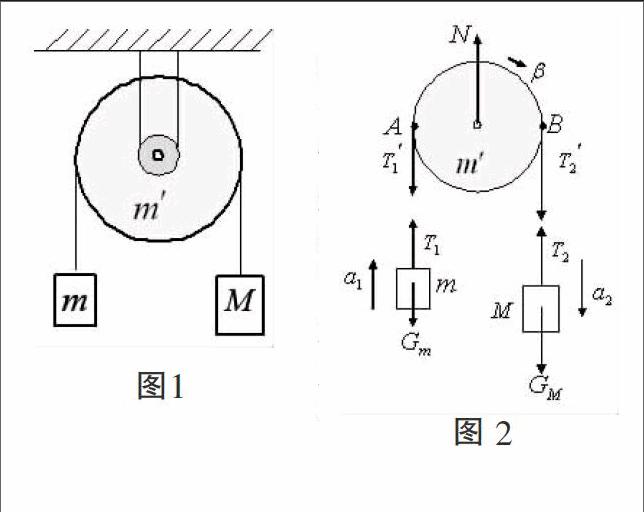
由西安通信学院朱峰老师主编的《大学物理》[1]及很多其他版本的《大学物理》教材和解题指导书上都有这样一道或者与之非常相似的题:一绳跨过定滑轮,两端分别系有质量分别为m和M的物体,且M>m。滑轮可看做是质量均匀分布的圆盘,其质量为m′,半径为R,转轴垂直于盘面通过盘心,如图1所示。由于轴上有摩擦,滑轮转动时受到的摩擦阻力矩为M■的作用。设绳不可伸长且与滑轮间无相对滑动。求物体的加速度及绳中的张力。
在该题的分析中有这样的叙述:“在滑轮绕轴做加速转动时,它必须受到两侧绳子的拉力所产生的力矩,以便克服转动惯性与阻力矩的作用。”在其他物理教材及习题指导书上对于类似的物理模型几乎都是这样叙述的。这样的表述让学生非常疑惑,因为滑轮受到的并不是绳子的拉力产生的力矩,而是绳子对滑轮的静摩擦力产生的力矩;其次,本题中滑轮两侧绳子中的张力不相等,高中阶段提到绳子的张力,每位教师都不忘提醒学生“同一根绳子上的张力处处相等”,但没有给此结论的附加条件,而该结论往往是学生解题时要用到的重要关系之一,因此,学生对此印象深刻。基于以上几点,很多学生对此题的讨论与解析有很多疑虑。本文就这几个问题展开相关讨论。
2.对原问题力矩的分析
绳的张力属于弹性力,其本质是原子间或分子间的电磁力,是由于组成绳的微观粒子之间的电磁相互作用力而产生的。当绳子的两端受到沿绳方向的拉力时,构成绳的分子偏离了原来的平衡位置,从而绳子内正负电荷的分布发生畸变,原有的电磁力平衡状态被破坏,使分子间出现引力或斥力占优的情况,亦即产生张力。从绳子张力的产生机理来看,绳子的张力具有“被动”的特点,即外力作用使绳子发生形变时,才产生张力,而且张力的大小、方向与外力迫使绳子发生的形变有关。设想在张紧的绳子上某位置作一假想的横截面,在假想的横截面两侧绳被分开的两部分之间相互施加的绳内拉力就是绳横截面的张力,属绳的内力,张力的方向沿绳的切线并指向绳伸长的方向[2];此外,绳子的两端和与之相连接的物体之间也存在相互作用的张力,属绳所受的外力,物体对绳的拉力方向也是沿着绳子切线并指向绳伸长的方向。因此,绳子的张力是绳上相邻两部分之间或绳子与和它相连接的物体之间的相互作用力。
显然,上述题中绳子的张力并没有作用在滑轮上,因而不可能对滑轮产生力矩。滑轮是因为受到绳子的静摩擦力的力矩才加速转动的。
3.对原问题的解析
滑轮及两侧物体的受力如图2,设两侧绳子中的拉力分别为T■和T■,两侧绳子在A、B两点的横截面分别受张力T■′和T■′,对与滑轮接触的AB段绳子而言,绳子内部的张力属内力。如果不计绳的质量,则T■′=T■,T■′=T■。同时,也是由于不计绳子质量,相对于转轴而言,AB段绳子受到的外力矩之和为零,即T■′、T■′,以及滑轮对绳子的静摩擦力f的力矩之和为零。而静摩擦力沿着相对运动趋势的负方向,即沿着滑轮的切线方向,则T■′、T■′与静摩擦力的力臂均为R,因此得T■′R-T■′R-fR=0
从而f=T■′-T■′
而对滑轮受到的绳的静摩擦力f′与f为作用力和反作用力的关系,因此有
f′R-M■=Jβ=(■m′R■)β
对于上下做平动的两物体,可以视为质点,由牛顿第二定律得
对m:T■-mg=ma
对M:Mg-T■=Ma
绳子与滑轮之间无相对滑动,因此滑轮边缘上一点的切向加速度和物体的加速度相等,即
a=a■=Rβ
联立以上方程,便可得到物体加速度a及绳中张力T■、T■。
对于类似的问题,有的教材[3]给出滑轮与绳子之间的摩擦力忽略不计的条件,这显然是错误的,这也是因为出题者错误地理解为是绳子的张力对滑轮施加了力矩,而不是绳子对滑轮的静摩擦力的力矩。显而易见的是,如果忽略绳子与滑轮之间的静摩擦力,滑轮则不可能转动起来,而绳子也不可能与滑轮之间没有相对滑动。此外,若能在题中说明不计绳子的质量则更严谨。
4.绳子的张力处处相等吗
显然,上述题中同一根绳子在滑轮两侧的张力是不相等的。这与中学老师强调的“同一根绳上的张力处处相等”是矛盾的,由于思维定势的负迁移影响,学生感觉同一根绳上张力不相等很费解。其实,“同一根绳上的张力处处相等”的传统结论是一种理想情况,是需要有附加条件的。实际的生活与生产中,几乎不存在绳子的张力处处相等的情况。学生在中学时遇到的相关物理问题,基本都是轻绳(不计绳子的质量)、轻质滑轮(不计滑轮的质量和转动惯量)、与绳子相连接的物体则可以视为质点等理想化模型的情况。学生不明白这一点,曾经习得的知识负迁移严重,才对该问题中两侧绳子的张力不相等非常费解。
根据前面谈到的绳子张力的本质,绳子各处的张力是否相等,取决于绳子各部分分子偏离原来的平衡位置的程度的高低,即取决于各部分绳子的“横截面”两侧正、负电荷的畸变情况,笼统地说“同一根绳上的张力处处相等”显然是不全面的,下面的例子用于说明这一点。
如图3所示,质量均匀分布的绳子长为L,质量为M,置于光滑的水平面上,在绳的一端施加拉力F,以绳的左侧端点为坐标原点,水平向右为x轴正向,对整段绳子,有F=Ma,则绳中距左侧长处的张力大小为T=■M·a=■F,因此绳上的张力并非处处相等。
图3 图4
如图4所示,质量为M的细绳悬挂于天花板上的A、B两点,A、B两点处的切线方向与天花板的夹角为θ,对整段绳而言,绳子受重力及A、B两点处天花板的拉力T,绳子内部的张力属内力。绳子在三个外力作用下平衡,则竖直方向合力为零,即2Tsinθ=Mg,则T=■。若截取左侧半段绳子来研究,则左侧半段绳子受到A处天花板的拉力T、重力及O点处绳的张力T′,如图5所示,绳子受到的水平方向的合力为零,可得到Tcosθ=T′,由此可见,O点处绳的张力T′与A、B两点处绳的张力也不相等。用同样的方法,可以得到绳左右两侧对于中心轴线对称的点的张力大小相等,方向沿各自的切线方向,但左侧和右侧绳上的不同点的张力大小都不相等。
由此看出,传统结论“同一根绳上的张力处处相等”是有附加条件的,即在一些理想化模型中,涉及的物体均可视为质点,而绳子为不计质量的理想的轻绳。如果绳子的质量不能忽略,或者问题涉及不能视之为质点的刚体,同一根绳上的张力通常是不相等的。
5.结语
物理教学是螺旋式上升的过程,很多知识点都不可能在一段时间内一次讲清楚,而是在教学中逐步加深和拓宽的。于是在教学中存在大量的知识的正迁移和负迁移现象。这就要求我们在教学中尽可能摆脱知识迁移的负面影响,促进知识的正向迁移,对有些暂时不能拓展的问题要留有余地,提醒学生慎用现成的结论,厘清规律的适用条件。同时要求学生在学习中不能死套结论。
参考文献:
[1]朱峰.大学物理[M].北京:清华大学出版社,2006:65-66.
[2]呼格吉尔,张良峰,邱为钢.末端悬挂重物转动绳子的研究[J].大学物理,2011,30(4):16-18.
[3]李春贵.大学物理(上册)[M].北京:中国水利水电出版社,2010:78.
