基于电流跟踪型SVPWM控制策略的SVG研究

李开鑫

（国网新疆电力公司电力科学研究院，乌鲁木齐　830011）



基于电流跟踪型SVPWM控制策略的SVG研究

李开鑫

（国网新疆电力公司电力科学研究院，乌鲁木齐830011）

摘要鉴于滞环控制有较好的响应速度，SVPWM控制能够提高直流电压的利用率，本文将滞环控制和SVPWM控制结合起来作为SVG的控制策略，仿真结果表明，电流跟踪型的SVPWM控制策略能够满足SVG无功检测和补偿的要求，同时验证了该控制算法的正确性与可行性。

关键词：滞环控制；空间矢量PWM；静止无功发生器

在配电系统中，广泛存在着感性设备，它们需要从电网中吸收大量的无功功率来实现自己的功能。无功功率在电网中传送，不仅降低了功率因数、增加了额外的能量损耗，也影响着用户的电能质量[1]。因此，研究无功补偿是非常必要的。

静止无功发生器（Static Var Generator，SVG）是最先进的无功补偿装置，具有传统无功补偿装置所没有的优势。本文以配电端SVG补偿无功为背景，利用基于瞬时无功理论的ip−iq检测算法，把电流跟踪型SVPWM控制策略[2-5]运用到SVG中，研究其补偿效果。

1　SVG的主电路拓扑结构

根据变换器电路采用电压源变换器（Voltage Source Converter，VSC）拓扑还是电流源变换器（CSC）拓扑，把SVG可分为电压源型和电流源型两种，由于电压源变换器（VSC）电路具有控制简单、运行效率高等优点，另外在低压系统中，不用串联和级联就可以满足SVG对器件的要求，故本文选择图1作为SVG的主电路拓扑。

图1　SVG基本电路结构

2　电流跟踪型SVPWM控制策略

2.1控制原理与实现方法

SVG的等值电路如图2所示。图中us(t)表示端电压矢量，uc(t)表示SVG输出电压矢量，ic(t)表示SVG输出电流矢量，L表示SVG的等效电感，il(t)表示负载电流。

根据电路原理，则可以写出方程：

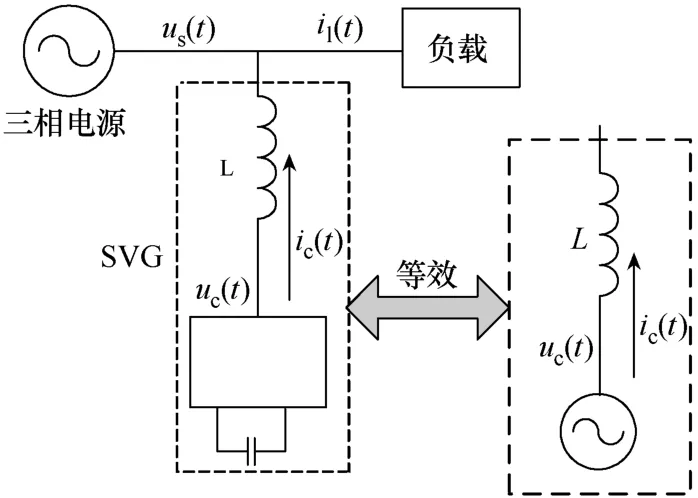
图2　SVG等值电路

整理可得

式（1）中，ic(t)表示SVG输出电流矢量，uc(t)表示SVG输出电压矢量，而us(t)表示端电压矢量，L和R分别表示SVG的等效电感和电阻。

令电流跟踪误差矢量为Δi(t)，则有

式（3）代入式（1）可写为

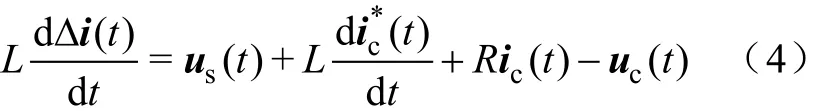
考虑到忽略其等值电阻，两式相减有

电流跟踪型SVPWM控制原理如图3所示。将无功指令电流i、i、i与补偿电流ia、ib、ic通过滞环比较单元，得到相应的比较状态值Ba、Bb、Bc，根据对V*的区域判别，最终由开关选择表，输出一个合适的Vk（k=0～7），使得三相VSC电流跟踪无功指令电流。

图3　电流跟踪型SVPWM控制原理

电流跟踪型SVPWM的SVG实现如图4所示，图中Udc表示SVG的直流电压，Ud表示SVG的直流参考电压，iload_abc表示负载三相电流，i_abc表示SVG指令电流，ic_abc表示SVG发出的补偿电流。

图4　基于电流跟踪型SVPWM的SVG控制框图

2.2矢量的选择规则

选取当前所需矢量的原则：

1）当|ΔI|＞IW时，选择的电压矢量Vk（k=0～7），必须使其对应的LdΔi(t)/dt具有与ΔI方向相反的最小分量，以保证电流矢量I在跟踪指令电流矢量I*的同时，限制电流变化率，以抑制电流谐波。

2）当|ΔI|≤IW时，原有矢量不进行切换。

根据选择规则，分析得到Vk的选择可遵循表1。

表1　V*、ΔI区域与Vk的选择

2.3ΔI区域检测

V*和ΔI区域叠加在一起如图5所示，ΔI的空间区域是将V*区域的空间坐标轴系（a、b、c）顺时针旋转π/6得到的，目的是有利于Δia、Δib、Δic正负极性的判别。

图5　电压矢量的选取原则

通过判断矢量Δi在三个坐标轴a、b、c上的分量Δia、Δib、Δic的正负极性，来确定Δi所在区域，而Δia、Δib、Δic可由滞环的输出直接判定。

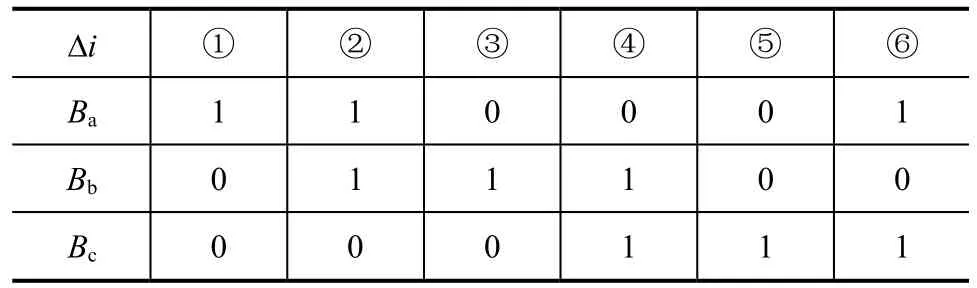
表2　Δi的区域判别

由表2和式（7），可得

式（8）中，RΔI（1）～RΔI（6）—ΔI区域1～6的逻辑变量。若ΔI位于j区域时，RΔI(j)=1，否则RΔI(j)=0，其中j∈(1～6)。

2.4u*的区域检测

图6中，Ⅰ～Ⅵ区域是由三条对角线组成的，这三条对角线分别对应于ua=0、ub=0、uc=0的情形，因此可以根据ua、ub、uc的符号来判别矢量u*所在区域。

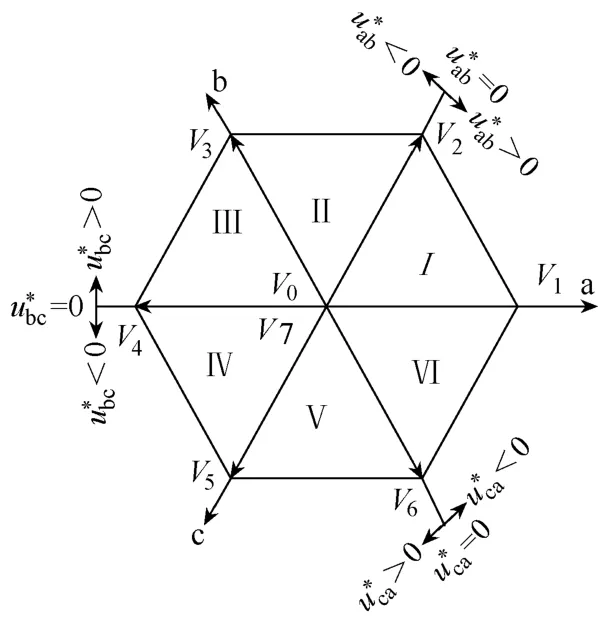
图6　u*的区域判别

表3　u*的区域判别

对于V*来说，显然可以通过Va*、Vb*、Vc*相关极性判别，且记

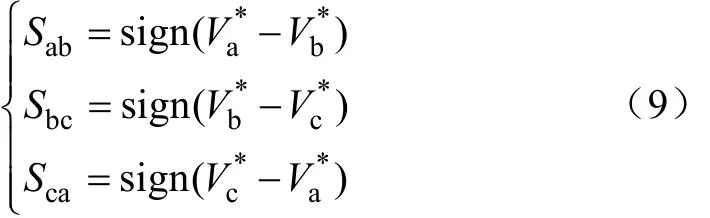
式（9）中，sign

结合上述信息,有Sab、Sbc、Sca包括参考电压矢量V*区域的信息，检测逻辑运算为

式（11）中，RV*(Ⅰ)～RV*(Ⅵ)—V*区域Ⅰ～Ⅵ的逻辑变量。若V*位于i区域时，RV*(i)=1，否则RV*(i)=0，其中i∈(Ⅰ～Ⅵ)。

2.5Vk选择的逻辑运算

要选定Vk（k=0～7），实际上只要确定开关函数Sa、Sb、Sc的状态即可。

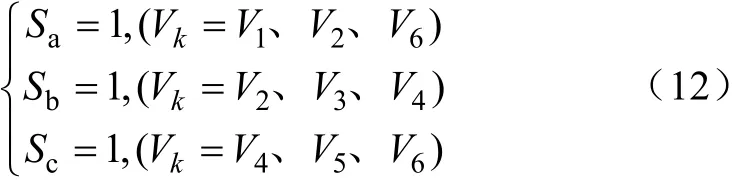
由表1、式（8）、式（11）、式（12）、综合分析可推出，三相VSC基于不定频滞环SVPWM的开关逻辑算式为

3　仿真

本文采用由POWERSIM公司开发的PSIM6.0软件进行仿真分析。设额定电压为380V，系统短路容量为20MV·A，则实际电源系统可用理想电压源与系统等值阻抗的串联来表示。

主要参数的选择：取等值电抗Ls=23μH，等值电阻Rs=0.0024Ω，交流连接电感Lc=4μH，直流电容C=23μF，直流电压的参考值Udc*=800V。

为了验证控制策略的正确性，假定0.1s前系统接入负载R=1Ω，L=12mH和R=2Ω，C=2.6mF之和，呈现阻感性负载，0.1s后切除负载R=1Ω，L=12mH部分，剩下阻容性负载。

图7是补偿前电网电压和补偿前电网电流（负载的电流）情况，可以看出，0.1s前电网电压超前于电网电流，呈阻感性，0.1s后电网电压滞后于电网电流，呈阻容性。

图8、图9、图10是分别在三种控制策略下的补偿效果图，由图可以看出，SVG投入后，三种控制策略均能平稳地实施动态无功补偿，补偿后功率因数接近于1.0，且动态补偿效果良好。

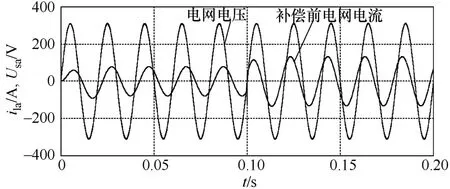
图7　电网电压和负载电流

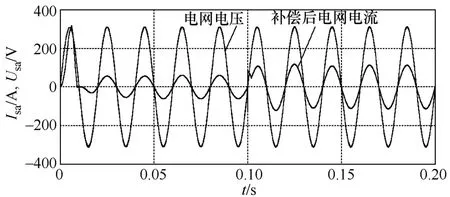
图9　基于滞环控制策略下电网电压和补偿后电网电流

图10　基于SVPWM控制策略下电网电压和补偿后电网电流

另外，由图11、图12、图13可知，在电流跟踪型SVPWM控制策略下，SVG开关有较低的动作频率，而开关动作频率的降低，能够减少开关动作次数，降低开关损耗，延长开关器件的寿命。

图11　基于电流跟踪型SVPWM控制策略下A相开关信号

图12　基于滞环控制策略下A相开关信号

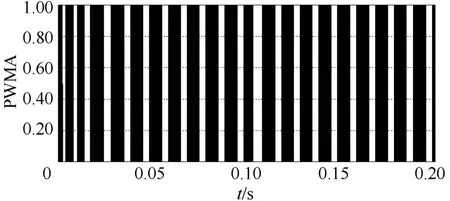
图13　基于SVPWM控制策略下A相开关信号

4　结论

本文将滞环控制技术和电压空间矢量脉冲调制技术相结合，应用于SVG的控制策略中，在PSIM仿真环境下，搭建了系统模型，仿真结果表明，这种控制策略能够满足SVG动态无功补偿的要求，同时验证了该控制策略应用于SVG中的可行性。

参考文献

[1] 王兆安, 杨君, 刘进军, 等. 谐波抑制和无功功率补偿[M]. 北京: 机械工业出版社, 1998.

[2] 张兴, 张崇巍. PWM整流器及其控制策略的研究[M]. 北京: 机械工业出版社, 2012.

[3] MartinezJA. EMTP simulation of a digitally-controlled static var system for optimal load compensation[J]. IEEE Transactions on Power Delivery, 1995, 10(3): 1408-1415.

[4] 雷元超, 陈春根, 陈国呈. 滞环比较PWM跟踪控制分析[J]. 水电能源科学, 2004, 22(1): 83-85.

[5] VlatkovicV, BorojevicD. Digital-signal-processor- based control of three-phase space vector modulated converters[C]//Applied Power Electronics Conference and Exposition, 1993: 888-894.

The Study of SVG based on Current-tracking SVPWM Control Strategy

Li Kaixin
(Power Research Institute of State Grid Xinjiang Electric Power Company, Urumqi830011)

Abstract In view of the hysteresis control having a good response speed, the SVPWM control can improve the utilization rate of dc voltage, this paper will combine the hysteresis control and the SVPWM control as SVG control strategy, the simulation results show that the current tracking type of SVPWM control strategy can satisfy the SVG reactive detection and compensation requirement, and at the same time it has verified the validity and feasibility of the control algorithm.

Keywords：hysteresis control; svpwm; static var generator