基于扩展有限元法及虚拟裂缝模型的混凝土断裂过程区分析
2016-03-15张晓东


摘要:提出一种利用扩展有限元法(eXtended Finite Element Method,XFEM)和虚拟裂缝模型对混凝土断裂过程区(Fracture Process Zone, FPZ)进行研究的方法.利用该方法可以求出裂缝扩展过程中混凝土FPZ的长度及位移和应力分布.利用该方法对一个三点弯曲混凝土梁进行研究,考察骨料粒径、不同软化律和不同初始裂缝长度对FPZ的影响.
关键词:混凝土; 扩展有限元法; 虚拟裂缝模型; 断裂过程区; 裂缝扩展; 软化律
中图分类号: TV313 文献标志码:B
Abstract:A method is proposed to study the Fracture Process Zone(FPZ) of concrete based on eXtended Finite Element Method(XFEM) and a fictitious crack model. The length, displacement and stress distribution of FPZ during the crack growth process can be obtained by the method. A threepoints bending concrete beam is studied and the effect of the aggregate size, different softening laws and different initial crack length on FPZ is studied.
Key words:concrete; extended finite element method; fictitious crack model; fracture process zone; crack growth; softening law
0 引 言
混凝土材料是一种准脆性材料,其断裂行为的重要特征是真实裂纹前方存在断裂过程区(Fracture Process Zone,FPZ).在这一区域存在微裂缝、集料互锁、粗糙表面的接触和摩擦等非线性现象,从而使得混凝土的断裂行为呈现非线性特性.[13]由于FPZ的尺寸通常与混凝土构件尺寸在同一数量级,采用传统的线弹性断裂力学分析混凝土结构的断裂问题已不适合.
FPZ是混凝土断裂力学中一个极为重要的概念.混凝土FPZ的研究与混凝土裂缝模型的研究紧密相关,按采用裂缝模型的不同,对混凝土FPZ的研究方法可大致分为2类.
1)基于黏聚裂缝模型的方法.这类模型适合于数值分析,其中适用于混凝土材料的黏聚裂缝模型又以虚拟裂缝模型[4]和裂缝带模型[5]为代表.
2)基于弹性等效裂缝模型的方法.这类模型一般用于解析计算混凝土结构断裂问题,按所使用的弹性等效原则的不同,这类裂缝模型又包括两参数断裂模型[6]、尺寸效应模型[7]、等效裂缝模型[8]和双K断裂模型[9].
由于解析裂缝模型的适用范围有限,本文重点关注黏聚裂缝模型,特别是虚拟裂缝模型.
虚拟裂缝模型将FPZ简化为一条虚拟的集中裂缝并将FPZ的非线性行为集中到该虚拟裂缝上考虑.采用虚拟裂缝模型结合传统有限元法,可以得到较为准确的裂缝扩展路径及虚拟裂缝面的张开位移和应力等物理量,但由于在传统有限元法中采用单元边界模拟裂缝,因此随着裂缝的扩展需不断进行网格重剖以保持单元边界与裂缝扩展路径一致[10],这极大地限制该方法的使用.
为克服传统有限元法分析断裂问题时遇到的网格重剖难题,BELYTSCHKO等[11]提出扩展有限元法(eXtended Finite Element Method,XFEM),基于单位分解定理,在传统有限元连续位移场中引入能描述裂纹两侧位移间断特性的非连续位移项,使裂纹的描述独立于计算网格,因而无须随着裂纹的扩展不断进行网格重剖.扩展有限元法结合虚拟裂缝模型被很多学者应用于混凝土结构的断裂问题研究,成功再现许多试验结果,显示出很好的应用前景.[1214]
本文提出一种基于XFEM和虚拟裂缝模型的混凝土FPZ计算方法,利用该方法可以准确计算混凝土结构裂缝扩展过程中虚拟裂缝的范围、张开位移和应力分布等.
1 虚拟裂缝模型的扩展有限元法
1.1 虚拟裂缝模型
虚拟裂缝模型是在黏聚裂缝模型的基础上发展而来的,该模型把混凝土裂缝分解为2部分(见图1):真实物理裂缝区(完全开裂区)和虚拟裂缝区(微裂区).[1]前者代表宏观的自由表面裂缝,裂缝表面无应力作用;后者将带状FPZ简化为一条分离裂缝,即虚拟裂缝,虚拟裂缝表面由于微裂缝作用、集料互锁等仍然可以承受应力作用,且承担应力的大小与虚拟裂缝的张开位移相关.虚拟裂缝模型概念清楚、模型简洁,被认为是基本的混凝土裂缝模型.
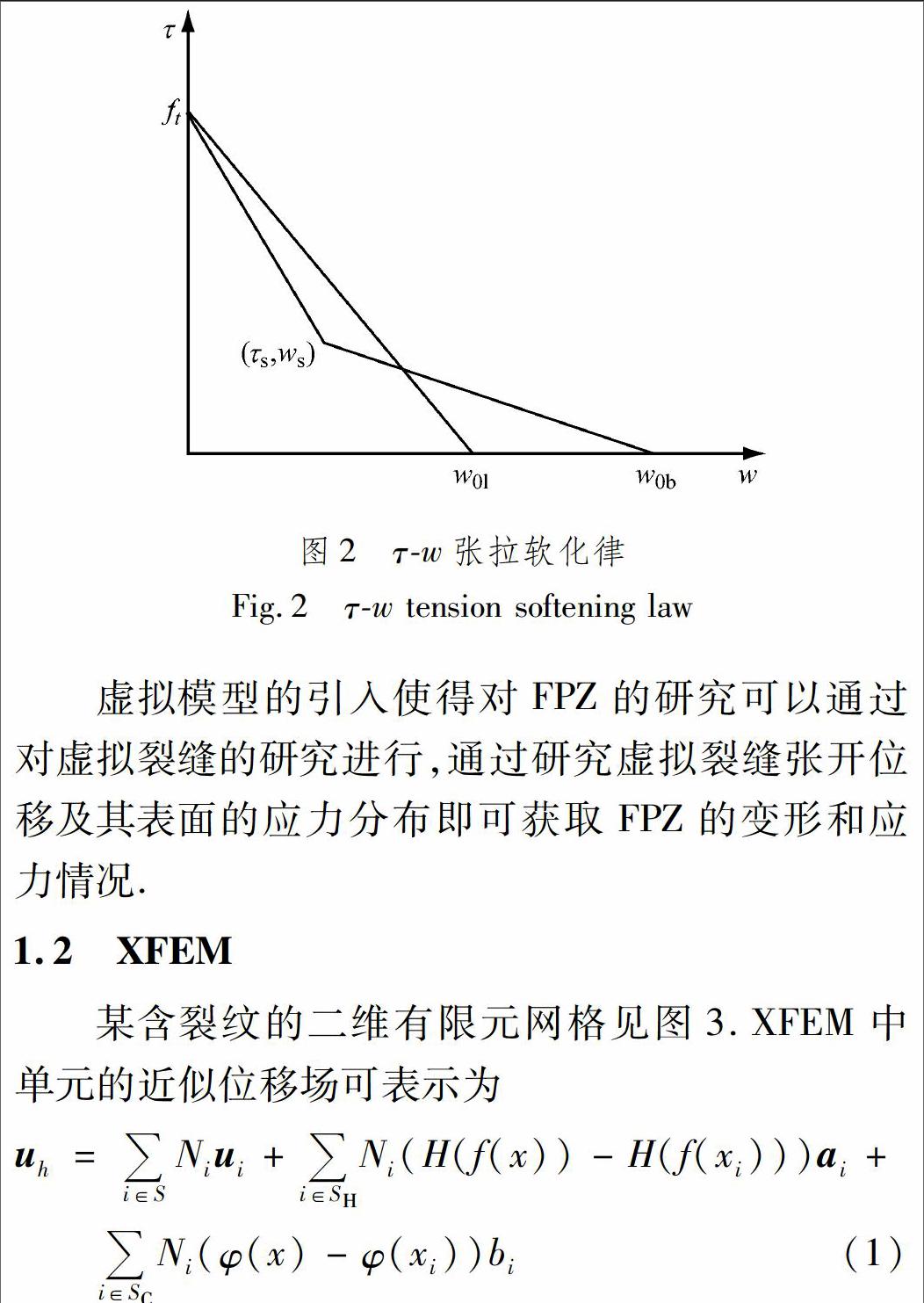
虚拟裂缝模型采用如下假定:1)材料非线性完全集中于虚拟裂缝区,虚拟裂缝以外的区域为线弹性材料;2)虚拟裂缝表面存在的黏聚应力τ与虚拟裂缝的张开位移w有关,一般可用τw张拉软化律曲线表示.常用的线性和双线性软化律见图2,曲线下方的面积即为混凝土材料的断裂能Gf=∫w00τdw,其意义是形成单位面积裂缝所吸收的能量.
虚拟模型的引入使得对FPZ的研究可以通过对虚拟裂缝的研究进行,通过研究虚拟裂缝张开位移及其表面的应力分布即可获取FPZ的变形和应力情况.
1.2 XFEM
由于虚拟裂缝面上的黏聚应力τ通常为虚拟裂缝张开位移的非线性函数,由式(5d)可知fcoh一般也为节点位移未知量的非线性函数,因此有限元方程系统的式(5a)和式(6)必须采用迭代方法求解.相关求解思路及裂缝扩展过程模拟方法可参见文献[14],这里不再详述.
2 虚拟裂缝计算方法
虚拟裂缝的范围及其上分布的黏聚应力和虚拟裂缝张开位移可以在有限元方程系统的迭代求解过程中予以求解,思路如下.
虚拟裂缝扩展路径被单元边界分割为许多候选虚拟裂缝段,见图5a.在计算过程中,对每个候选虚拟裂缝段计算其高斯积分点上的裂缝张开位移w.
1)首先由裂缝扩展路径计算裂缝与单元边界交点在整体笛卡尔坐标系下的坐标xi和xj,见图5b.
求得高斯点的裂缝张开位移后,判断候选虚拟裂缝段属于黏聚裂缝还是真实裂缝,仅当候选虚拟裂缝段上所有高斯点的张开位移w均满足0≤w≤w0时,才认为该段裂缝位于FPZ,属于黏聚裂缝;若有至少一个高斯点张开位移满足w>w0,则该裂缝段成为自由表面裂缝.
在每一次平衡迭代计算过程中均需对所有的候选虚拟裂缝段进行上述计算.同时需注意,一旦候选虚拟裂缝段变成真实裂缝的一部分,则在后续计算中该裂缝段将不再作为候选的虚拟裂缝段.在计算过程中,对每一个裂缝段采用3个高斯点计算其张开位移.
当系统平衡方程得到满足时,黏聚裂缝段及其高斯点的张开位移即被确定,同时还可计算其长度和黏聚应力分布,从而确定FPZ的长度、张开位移和应力分布.
3 数值算例
3.1 算例1 双悬臂梁
对于该算例,文献[13]给出用伪边界积分(Pseudo Boundary Integral,PBI)方法得到的解,本算例以此作为比较的标准.由于在伪边界积分方法中裂纹的扩展路径是预先指定的,为保持一致性,本算例指定裂缝沿水平方向扩展,即沿图6中虚线所示路径扩展.有限元模型采用119×59的均匀网格,按平面应变问题进行计算,裂缝每一步扩展长度为4 mm.
图7和8分别给出裂缝扩展至第9、34和58步时的虚拟裂缝张开位移和虚拟裂缝表面的应力分布.图中的裂缝张开位移和裂缝表面应力分别用临界裂缝张开位移w0和混凝土抗拉强度ft进行无量纲化处理.
计算结果显示采用本文方法计算得到的虚拟裂缝张开位移和表面应力分布与文献[13]给出的结果完全一致,这说明本文方法和程序准确.
3.2 算例2 三点弯曲混凝土梁试件
混凝土梁试件见图9.梁的几何尺寸为:厚度t=b=150 mm,l=600 mm.取文献[15]给出的C3等级的混凝土进行研究,其弹性模量和抗拉强度分别为E=34.65 GPa,ft=3.5 MPa,计算时取ν=0.1.
3.2.1 不同骨料粒径及不同软化律的影响
考虑3种不同骨料粒径对FPZ的影响,对应的
最大骨料粒径dmax分别为8,16和32 mm.不同的骨料粒径主要影响混凝土材料的断裂能,3种骨料粒径对应的断裂能及采用线性和双线性软化律所需的参数见表1.
对应峰值载荷时虚拟裂缝表面的张开位移和应力分布分别见图10和11.不论是采用线性软化律还是双线性软化律,不同骨料粒径对应的虚拟裂缝表面张开位移和表面应力分布呈大致相同的规律,但FPZ的长度却不同.大致来说,骨料粒径越大,对应峰值载荷的FPZ长度越大,特别是采用线性软化曲线时这种现象非常明显.需注意的是,当载荷达到峰值载荷时,混凝土FPZ并未发展至饱和程度,这可以从图10中x=0时w
裂缝扩展过程中FPZ长度最大时虚拟裂缝表面的位移和应力分布分别见图12和13.
不同骨料粒径对应的虚拟裂缝表面的位移分布遵循的基本规律相同,但采用线性软化律和双线性软化律得到的虚拟裂缝表面应力分布却大不相同.这是因为此时FPZ已充分发展.从图12和13中可以看出:x=0时,虚拟裂缝张开位移已经达到临界值w0,而对应的虚拟裂缝表面应力为0;在整个FPZ上位移从0至w0连续变化,由于双线性软化律曲线存在转折点,因此此时的应力分布曲线也必然出现转折点.
加载过程中FPZ长度随所加集中载荷的变化曲线见图14.不论是采用线性软化律还是双线性软化律,当载荷相同时,FPZ长度随骨料粒径增加而增大;FPZ长度在峰值载荷处并未达到最大值,在峰值载荷过后裂缝进入非稳定扩展路径并扩展至一定阶段时,FPZ长度达到最大值.在骨料粒径相同的情况下,采用双线性软化律得到的FPZ长度大于采用线性软化律得到的长度;采用双线性软化律得到的峰值载荷和FPZ长度最大时对应的载荷均小于采用线性软化律时得到的结果.
3.2.2 不同初始裂缝长度影响
为考察不同初始裂缝长度对虚拟裂缝张开位移和表面应力分布的影响,考虑线性软化律情况,令初始裂缝长度从0.01b变化至0.25b.
不同初始裂缝长度时虚拟裂缝张开位移和表面应力分布分别见图15和16.
随着初始裂缝长度的增大,虚拟裂缝张开位移增大,而虚拟裂缝的表面应力变小.需指出的是,在初始裂缝从0.01b变化至0.25b过程中,虚拟裂缝长度保持不变;若初始裂缝长度达到0.30b,则虚拟裂缝的长度会发生变化.
4 结 论
提出一种利用XFEM结合虚拟裂缝模型对混凝土FPZ进行研究的方法,数值算例表明该方法准确可靠.对一个三点弯曲混凝土梁试件在裂缝扩展过程中的FPZ特性进行研究,结果如下.
1)不同骨料粒径对应的混凝土FPZ的位移和应力分布遵循大致相同的规律.
2)在外载荷达到峰值载荷时,混凝土FPZ并未发展至饱和程度;在峰值载荷过后,当结构裂缝继续非稳定扩展至某一阶段时混凝土FPZ方发展至饱和.
3)在相同载荷水平下,骨料粒径越大,对应的FPZ长度越大.
4)随着结构初始裂缝长度的增大,FPZ的张开位移增大,而应力却减小.
本文提出的方法原则上适用于任意复杂结构裂缝扩展过程中的FPZ的研究,且可以考虑任意软化律,但本文只对I型断裂问题进行验证,对于II型甚至复合型断裂问题,本文方法是否有效尚需进一步研究.
参考文献:
[1]徐世烺. 混凝土断裂力学[M]. 北京: 科学出版社, 2011: 129169.
[2]陈瑛, 姜弘道, 乔丕忠, 等. 混凝土黏聚开裂模型若干进展[J]. 力学进展, 2005, 35(3): 377390.
CHEN Ying, JIANG Hongdao, Qiao Pizhong, et al. Developments on concrete cohesive model[J]. Advances in Mechanics, 2005, 35(3): 377390.
[3]卿龙邦, 李庆斌, 管俊峰, 等. 基于虚拟裂缝模型的混凝土断裂过程区研究[J]. 工程力学, 2012, 29(9): 112116.
QING Longbang, LI Qingbin, GUAN Junfeng, et al. Study of concrete fracture process zone based on fictitious crack model[J]. Engineering Mechanics, 2012, 29(9): 112116.
[4]HILLERBORG A, MODER M, PETERSON P E. Analysis of crack propagation and crack growth in concrete by means of fracture mechanics and finite elements[J]. Cement and Concrete Research, 1976, 6(6): 773782.
[5]BAANT Z P, OH B H. Crack band theory for fracture of concrete[J]. Matériaux et Construction, 1983, 16(3): 155177.
[6]JENQ Y S, SHAH S P. Two parameter fracture model for concrete[J]. Journal of Engineering Mechanics, 1985, 111(10): 12271241.
[7]BAANT Z P. Size effect in blunt fracture: concrete, rock, metal[J]. Journal of Engineering Mechanics, 1983, 110(4): 518535.
[8]NALLATHAMBI P, KARIHALOO B L. Determination of specimensize independent fracture toughness of plain concrete[J]. Magazine of Concrete Research, 1986, 38(135): 6776.
[9]XU S L, REINHARDT H W. A simplified method for determining doubleK fracture parameters for threepoint bending tests[J]. International Journal of Fracture, 2000, 104(2): 181209.
[10]杨庆生, 杨卫. 断裂过程的有限元模拟[J]. 计算力学学报, 1997, 14(4): 3338.
YANG Qingsheng, YANG Wei. Finite element simulation of fracture process[J]. Chinese Journal of Computational Mechanics, 1997, 14(4): 3338.
[11]BELYTSCHKO T, GRACIE R, VENTURA G. A review of extended/generalized finite element methods for material modeling[J]. Modelling and Simulation in Materials Science and Engineering, 2009, 17(4): 043001.
[12]MOS N, BELYTSCHKO T. Extended finite element method for cohesive crack growth[J]. Engineering Fracture Mechanics, 2002, 69(7): 813833.
[13]ZI G, BELYTSCHKO T. New cracktip elements for XFEM and applications to cohesive cracks[J]. International Journal for Numerical Methods in Engineering, 2003, 57(15): 22212240.
[14]张晓东, 丁勇, 任旭春. 混凝土裂纹扩展过程模拟的扩展有限元法研究[J]. 工程力学, 2013, 30(7): 1421.
ZHANG Xiaodong, DING Yong, REN Xuchun. Simulation of the concrete crack propagation process with the extended finite element method[J]. Engineering Mechanics, 2013, 30(7): 1421.
[15]SHAH S P. Fracture toughness of cementbased materials[J]. Materials and Structures, 1988, 21(2): 145150.
(编辑 武晓英)
