构建以“问题为串,练习为线”的教学新模式
2016-03-11李月红
李月红
[摘 要]学生学习数学离不开有条有理、有根有据的思维。通过“问题为串,练习为线”的教学新模式,开启学生思维的闸门,教给学生独立思考的方法,拓宽学生思维的空间;引导学生在实践中合作,在合作中交流,在交流中研讨,在研讨中构建知识体系。
[关键词]问题串 练习线 教学模式
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2016)05-068
【模式简介】
教师“教”的方式始终并直接关系着学生“学”的方式。虽然教无定法,贵在得法,但不可否认教学有法。
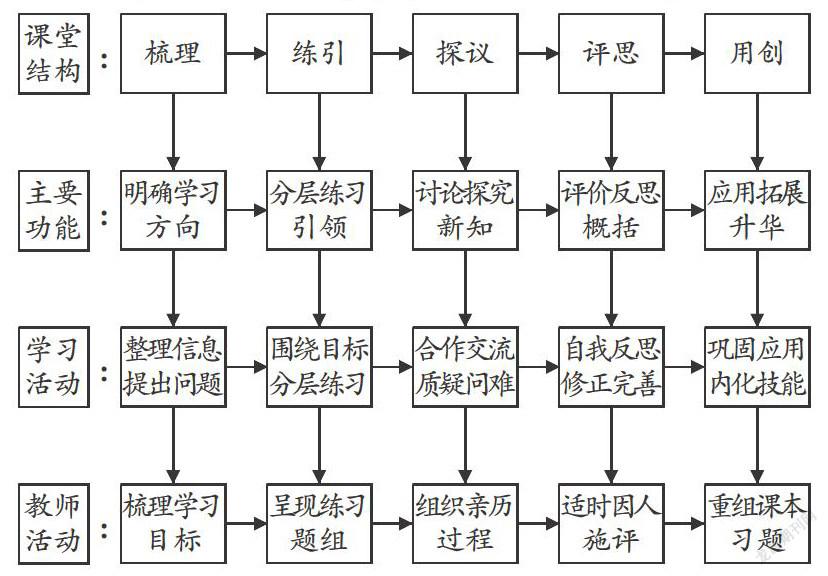
教学中我在目标、结构、学法上进行了探索,在目标上坚持“五以”:以认知为基点,以发展为根本,以创新为核心,以情感为动力,以评价为手段;在结构上把握“五度”:“梳”“理”有维度,“练”“引”有梯度,“探“”议”有深度,“评”“思”有效度,“用”“创”有广度。在此基础上形成了十字五环节“以问题为串,练习为线”的教学模式。
【教学内容】
北师大版四年级数学下册第27~28页。
【教学目标】
1.通过直观操作活动,感悟、体验三角形的内角和是180度。
2.通过验证和交流初步培养学生的交流能力、协作能力和动手实践能力。
3.能应用三角形内角和的知识解决一些简单的实际问题。
【教学过程】
一、情境引入,提出问题
师:之前我们一直在研究三角形,今天还将继续学习三角形的有关知识,让我们一起去三角形的王国里看看吧!
(课件出示:3种三角形的争论)
师:看了这个情境,你能说说它们发生了什么事情吗?
生1:3个三角形在争论谁的内角和大。
师:原来是每个三角形都认为自己的内角和大。
(板书课题:三角形的内角和)
师:看到这个问题,你想提出什么问题呢?
生2:我想知道哪个三角形的内角和大。
生3:我想知道三角形的内角和是多少。
生4:我想知道三角形的内角和与三角形的形状有没有关系。
生5:我想知道三角形的内角和与三角形的大小有没有关系。
【设计意图:从学生喜闻乐见的动画片入手,让学生品味情境,激发学生的学习情感,促使学生在认知冲突中明确学习目标。】
二、创造图形,初步探究
师(出示长方形、正方形、梯形):请同学们拿出长方形、正方形、梯形,在长方形、正方形、梯形这些图形中画、折或剪出三角形。
(学生活动:画、折、剪三角形)
师:你手中的三角形的内角和是多少呢?
(学生活动:初步探究三角形的内角和)
师:谁能说说你手中的三角形是怎么来的,内角和是多少,你是怎么知道的?
生1:我的等腰直角三角形是从正方形里得来的。三角形的内角和是180度。(生1演示并说明理由)
生2:我的三角形是直角三角形,是从长方形里得来的,内角和是180度。(生2演示并说明理由)
师:同学们真棒!通过给正方形和长方形加对角线的方法得到了直角三角形,并知道了这些直角三角形的内角和是180度。
(课件分别演示正方形和长方形沿对角线折或剪下的直角三角形内角和是180度的验证过程)
【设计意图:巧妙地利用正方形、长方形和梯形,通过画对角线或沿对角线折剪的方式得到三角形,并通过初步探究从正方形和长方形里得到直角三角形,打开了探索三角形内角和的思维闸门。】
三、深入探究,合作交流
师:你们从梯形中得到了什么样的三角形?
生1:我的是锐角三角形。
生2:我的是钝角三角形。
师:从梯形中得到的三角形的内角和是不是也是180度呢?
1.探索验证方法
(小组充分讨论后反馈验证方法)
师:请说一说你是用什么方法来验证的。
(全班交流验证方法)
2.小组合作交流验证内角和
师:大家想出了量一量、拼一拼、折一折的方法,现在就以小组为单位,小组成员分工合作,对每一种三角形进行研究验证。请看小组合作要求。
(课件出示小组合作要求)
3.学生汇报交流验证的方法和结果
师:请把你们验证的方法和结果说一说。
师:你研究的是什么三角形?用了什么方法?
生1:我验证的是锐角三角形,用了量的方法。
师:你量得的结果怎样?
师:还有哪些同学用了量的方法,你们的结果是怎样的?
师:还有其他不同的验证方法吗?
生2:拼的方法。
师:还有谁有不同的方法?
生3:折一折的方法。
师:现在用电脑来演示验证的方法。
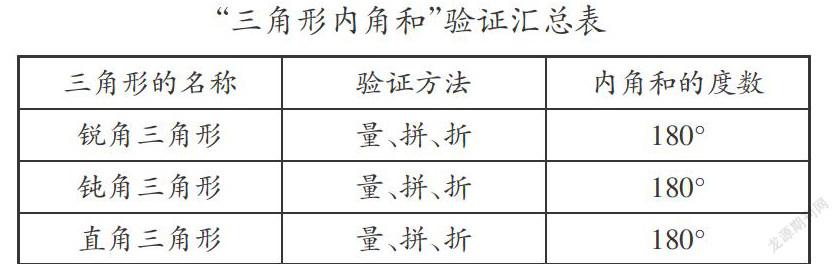
(课件演示三种三角形拼、折的过程和一张验证结果表)
【设计意图:让学生在量一量、拼一拼、折一折的操作活动中思考,从而发现所有三角形的内角和都是180度。学生的操作材料和操作开放度虽然不同,但学生通过操作中的“悟”,加深了对知识的理解,通过验证升华知识、完善结论,学生的思维水平得到了提高。】
师:从验证结果中你发现了什么?
生4:所有三角形的内角和都是180度。
师:大家刚才用量的方法得到三角形内角和不是正好180度,那是测量时的误差造成的。实际上所有三角形的内角和都是180度。学习了三角形内角和的知识后,你们能解决刚才三角形王国里的三种三角形争论的问题吗?
生5:它们的内角和都一样大,都是180度。
师(出示一个小三角形):这个三角形的内角和是多少呢?(出示一个大三角形)这个大三角形呢?为什么?
生6:它们都是三角形,内角和都是180度。
师(总结):不论三角形的大小、形状怎样,它的内角和都是180度。
【设计意图:最后让学生对不同大小的三角形的内角和进行判断与总结,在验证形状的基础上补上“大小”,学生的知识结构和认知结构就更加完整了。这样的设计有助于学生以后学习的正迁移。】
四、应用深化
1.课本第28页第3题
师:请算出角A的度数。
(全班交流时小结:已知直角三角形的一个锐角度数,求另一个锐角度数时也可以直接用90度减去已知锐角的度数。)
2.第29页练一练第1题
学生独立完成后全班交流。
3.练一练第2题。
学生在独立思考后汇报,说明理由。
4.把一个大三角形分成两个小三角形,请问每个三角形的内角和是多少?
师(将一个大三角形剪成两个小三角形):这个大三角形的内角和是多少?剪成这样的两个小三角形后,这个小三角形的内角和是多少?如果再接着剪成更小的三角形,内角和是多少?
【设计意图:生动、活泼、有目的性、有针对性、有层次、形式多样的练习,既能帮助学生巩固已学的知识,又充满了浓浓的数学味,促进了学生思维发展的同时,还渗透了“变”与“不变”的辩证唯物主义的思想教育。】
五、反思总结
师:通过这节课的学习,你最大的收获是什么?你都学到了哪些方法呢?
(责编 金 铃)
