简单函数方程的解法
2016-03-11龚浩生,张留杰,童嘉森
简单函数方程的解法
◇北京龚浩生1张留杰1童嘉森2(特级教师)
在高中学习函数时,我们常遇到下面的一类问题:
例1已知f(x)满足2f(x)+f(1/x)=3x,求f(x)的解析式.
这类问题很多同学都感到无从下手,因为在教材中没有涉及它们的解法,即便有的老师讲过类似的例题,但很多同学仍然一知半解.
这类问题属于函数方程的问题,本文介绍几种简单函数方程的解法.
1什么是函数方程
我们知道,如2x2+1=3x这样含有未知数的等式叫方程,其中的未知数x代表数值,故这样的方程也叫数值方程.而例1、2中的等式是含有未知函数在内,故它们就叫作函数方程,满足函数方程的函数就叫作函数方程的解,求函数方程的(一些或全体)解或确定无解的过程就叫做解函数方程.
有关函数方程的问题常在数学竞赛与大学自主招生考试中出现,高考中也时常会有它们的身影,这类问题一般属较难题,没有固定的解题模式,常常需要一些特殊技巧综合很多知识与方法.
下面我们探讨几种相对简单的函数方程的解法.
2简单函数方程的解法
2.1 待定系数法
在知道函数方程中的未知函数的类型(如多项式函数、指数函数、对数函数等)时,可用待定系数法求解.即先设出函数解析式,代入函数方程,再变形整理、比较系数而求解.
例3已知f(x)为多项式函数,解函数方程f(x+1)+f(x-1)=2x2-4x.
因为f(x)为多项式函数,而f(x+1)与f(x-1)并不会改变f(x)的次数,故由原函数方程知f(x)为二次函数,设f(x)=ax2+bx+c, 则
f(x+1)=a(x+1)2+b(x+1)+c=
ax2+(2a+b)x+(a+b+c),
f(x-1)=a(x-1)2+b(x-1)+c=
ax2+(b-2a)x+(a-b+c).
故
f(x+1)+f(x-1)=2ax2+2bx+2(a+c)=2x2-4x.

一般来说,解函数方程最后都要检验所求得的函数是否满足原来的函数方程.
2.2 变量代换法
把函数方程中的自变量适当地赋以另外的变量形式,构造出多个函数方程进行求解,代换时注意保持函数定义域不变.这是较为常用的一种方法.
例2解答如下.
令x=t(t≠1),得
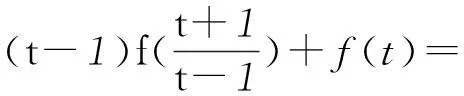
①


②
由式②×(t-1)-①,得f(t)=1,所以f(x)=1 (x∈R,x≠0),代入原函数方程,易知其满足方程.

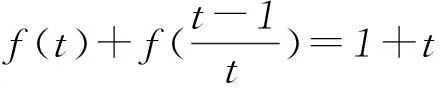
③

④
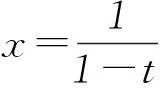

⑤
由式③-④+⑤得
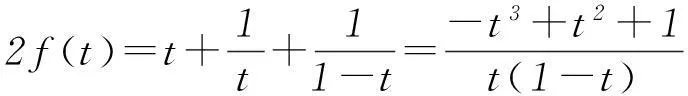

2.3 函数迭代法
对于形如f(x)+f[φ(x)]=u(x)(u(x)已知)的函数方程,若存在正整数k,使得φk(x)=x,而对小于k的整数m,φm(x)≠x(其中φk(x)=φ(φk-1(x))=φ(φ(φk-2(x)))=…),即φ(x)具有迭代周期,那么也可用如下的迭代法进行求解.
例4另解如下.



此时可将原方程表示为
f(x)+f(φ(x))=1+x,
⑥
迭代一次可得
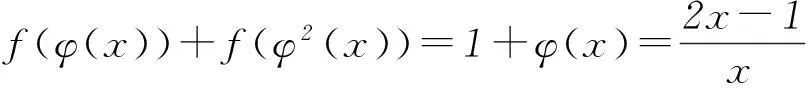
⑦
再迭代一次可得


⑧

2.4 数值代入法
当函数方程中的独立变量多于1个时,可将其中部分的独立变量以具体的数值或某一个相同的变量代入,从而简化方程进行求解.
例5已知函数f(x)满足:f(0)=1,f(π/2)=2,且对任意的x、y∈R,有
f(x+y)+f(x-y)=2f(x)cosy,
⑨
试求f(x)的解析式.
令x=0、y=t,代入式⑨可得
f(t)+f(-t)=2f(0)cost=2cost.
⑩

f(t+π)+f(t)=0.
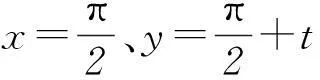
f(t+π)+f(-t)=-2f(π/2)sint=-4sint.
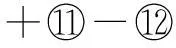
更一般地,若f(0)=a, f(π/2)=b,则式⑨的解为
f(x)=acosx+bsinx.
因为若f(x)=acosx+bsinx,则
f(x+y)+f(x-y)=[acos (x+y)+bsin (x+y)]+
[acos (x-y)+bsin (x-y)]=
a[cos (x+y)+cos (x-y)]+
b[sin (x+y)+sin (x-y)]=
2acosxcosy+2bsinxcosy=
2(acosx+bsinx)cosy=2f(x)cosy.

例6求定义在R上的增函数f(x),满足对任意x、y∈R,有
f(f(x)+y)=f(x+y)+f(0) .

f(f(x)-x)=2f(0).

f(f(y)+x)=f(x+y)+f(0).

f(f(y)-y)=2f(0).

f(f(x)-x)=f(f(y)-y).
由函数f(x)的单调性得f(x)-x=f(y)-y,即存在常数c,使得对一切实数x,有f(x)=x+c,经检验,它满足给定的条件.
2.5 柯西法与柯西方程
用柯西法求解函数方程的一般步骤是:先求出对于自变量取自然数时解的形式,然后依次证明对自变量取整数、有理数以及实数时函数方程的解仍然具有这种形式,从而得到函数方程整体的解.
例7(2006年复旦大学自主招生卷)f(x)在[1,+∞)上单调递增,且对∀x、y∈[1,+∞),都有f(x+y)=f(x)+f(y)成立.
证明:存在常数k使f(x)=kx在x∈[1,+∞)上成立.
证明设f(1)=k,由题设对∀n∈N*⊆[1,+∞),有f(n+1)=f(n)+f(1)=f(n)+k,于是
f(n)=kn.
对任意的有理数
q/p∈[1,+∞) (p、q∈N*,q≥p)
有
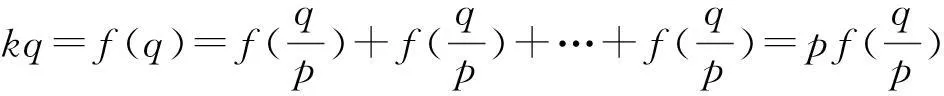

对任意的无理数t∈[1,+∞),可取在[1,+∞)上单调递增的有理数列{rn}与单调递减的有理数列{sn},且rn≤t≤sn,rn→t、sn→t,由于f(x)在[1,+∞)上单调递增,所以krn=f(rn)≤f(t)≤f(sn)=ksn,令n→∞,即有f(t)=kt.
所以,存在常数k使f(x)=kx在x∈[1,+∞)上成立.
形如f(x+y)=f(x)+f(y)(x、y∈R)的函数方程,叫做柯西方程.关于柯西方程有如下结论:
定理若满足柯西方程的函数f(x)是连续的,或单调,或在f(x)零点的某个邻域中有界,则柯西方程的解为f(x)=ux(其中u=f(1)).
与柯西方程相关的问题或可化为柯西方程解决的函数方程问题在各类考试中也较为常见.
例8(乌克兰国立基辅大学数学竞赛试题) 求证所有函数f: R→R,它在点x=0连续且对所有x、y∈R满足关系式.
f(x+y)=f(x)+f(y)+xy(x+y).
证明转化为柯西方程处理,由
f(x+y)=f(x)+f(y)+xy(x+y)⟹



g(x+y)=g(x)+g(y).

例9(2008年重庆卷) 若定义在R上的函数f(x)满足:对∀x1,x2∈R,有
f(x1+x2)=f(x1)+f(x2)+1.
下列说法一定正确的是().
Af(x)为奇函数; Bf(x)为偶函数;
Cf(x)+1为奇函数;Df(x)+1为偶函数
由f(x1+x2)=f(x1)+f(x2)+1⟹
f(x1+x2)+1=(f(x1)+1)+(f(x2)+1).
令g(x)=f(x)+1,则原方程为g(x1+x2)=g(x1)+g(x2),当f(x)为单调函数时,g(x)也为单调函数,由定理有g(x)=g(1)x,即f(x)+1=g(1)x,故只有选项C正确.
例10(2008年陕西卷) 定义在R上的函数f(x)满足f(x+y)=f(x)+f(y)+2xy(x、y∈R),f(1)=2,则f(-3)=().
A2;B3;C6;D9
由f(x+y)=f(x)+f(y)+2xy,可得f(x+y)-(x+y)2=(f(x)-x2)+(f(y)-y2),令g(x)=f(x)-x2,则原方程可化为
g(x+y)=g(x)+g(y).
当x∈Z时,由柯西方法可得g(x)=g(1)x,所以f(x)=g(1)x+x2.
又由f(1)=2可得g(1)=1,故f(x)=x+x2,f(-3)=-3+9=6,故选项C正确.
