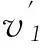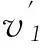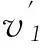活用题根 决胜高考———以一维弹性碰撞为例
2016-03-11王跃军
活用题根决胜高考———以一维弹性碰撞为例
◇湖南王跃军
在历届高考中,碰撞问题是必考热点,而一维的弹性碰撞问题更为常见.我们若能重视教材、挖掘教材、拓展教材,熟悉公式结论的数学推导过程,并熟记相关的重要的二级结论,做到巧学活用,则在高考中必能事半功倍.
人教版物理《选修3-5》第16章第4节“碰撞”中的思考与讨论有下面物理情景及结论.
1物理情景一
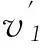

图1
碰撞前后
m
1
和
m
2
组成系统动量守恒,则
. 弹性碰撞前后该系统机械能守恒,则

由上解得2个物体碰撞后的速度分别为

(结论1)
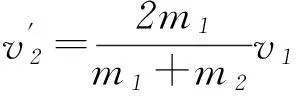
(结论2)
本题型中的动量守恒和机械能守恒方程很容易得出,但是计算过程需要耗费较多时间,若在解题中我们能熟记该物理情景下的结论,在遇到类似问题时,特别是选择题、填空题时,我们就可以直接利用结论进行快速解题.
例1(2014年大纲卷) 一中子与一质量数为A(A>1)的原子核发生弹性正碰.若碰前原子核静止,则碰撞前与碰撞后中子的速率之比为().
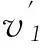

故正确选项为A.

(1) 用重水和石墨作减速剂,哪种减速效果更好?
(1) 设中子质量为mn, 靶核质量为m, 中子碰前速度为v0, 中子碰后速度为v1, 靶核碰后速度为v2, 由动量守恒定律和机械能守恒定律得
mnv0=mnv1+mv2,

解得中子碰后速度

靶核碰后速度为
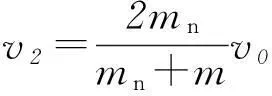
在重水中靶核质量mH=2mn,则


在石墨中靶核质量mC=12mn.
同理可得

由于v1H 2物理情景二 图2 碰撞前后 m 1 和 m 2 组成的系统动量守恒,得 又碰撞前后m1和m2组成的系统机械能守恒 由上可得2个物体碰撞后的速度分别为 (结论3) (结论4) 讨论1若m1=m2,则有 也就是说,当2个质量相同的物体发生弹性碰撞,那么,这2个物体将会交换它们的速度. 讨论2若v2=0,则有 这便是教材上的物理情景一,可见情景一是情景二的一种特殊情况.结论3和结论4看似比较复杂,但是仔细观察我们会发现等式右边的分母是一样的,分子的下标1和2是相反的,再结合结论1和结论2来记忆,相信会更有帮助. 例3(2015年福建卷改编) 如图3所示,2滑块A、B在光滑水平面上沿同一直线相向运动,滑块A的质量为m,速度大小为2v0,方向向右,滑块B的质量也为m,速度大小为v0,方向向左,2滑块发生弹性碰撞后的运动状态是(). 图3 AA和B都向左运动; BA和B都向右运动; CA静止,B向右运动; DA向左运动,B向右运动 故滑块A碰撞后向左运动. 再由结论4得 故滑块B碰撞后向右运动,所以本题选项D正确. 其实,本题作为选择题,我们可以直接用讨论1的结论:当2个质量相同的物体发生弹性碰撞,那么,这2个物体将会交换它们的速度.从而更快得到正确答案. 对于一维的弹性碰撞,解题时我们一般对系统运用动量守恒及机械能守恒列出等式即可求解,若在高考时才运用数学知识进行化简计算,会耗费太多的时间,这在高考中是不划算的.另外,我们平时应重视教材、挖掘教材、举一反三、巧学活用,当然平时也应加强公式结论的数学推导过程,并且能熟记相关的公式结论.这样在正式的考试中,我们便能省去其中的数学运算过程,从而达到事半功倍的效果. (作者单位:湖南省怀化市湖天中学) 宇宙中的未解之谜——类星体 类星体指一类特别明亮、体积特别小、运行速度特别大、发射出的能量特别强又有极快的明暗周期变化的一类天体.美国天文学家马丁·斯密特等人对类星体做了深入研究总结出一些现象,提出了一些令人费解的问题,但直至今天,天文学家们连在类星体到底是离我们较近的天体还是离我们非常遥远的天体这一点上还没有完全达成共识,类星体到底是什么东西就更是不得而知.