大坝风险分析的计算方法：进展和挑战

Ignio Esuder-BuenoInstitute for Wter nd Environmentl Engineering Universitt Politèni de Vlèni Vleni 46022 Spin* Guido MzzàRier sul Sistem Energetio—RSE SpA Miln 20134 Itly Adrián Morles-TorresiPress Risk Anlysis Vleni 46023 Spin Jesi T. Cstillo-RodríguezInstitute for Wter nd Environmentl Engineering Universitt Politèni de Vlèni Vleni 46022 Spin

大坝风险分析的计算方法：进展和挑战

Ignacio Escuder-BuenoaInstitute for Water and Environmental Engineering, Universitat Politècnica de València, Valencia 46022, Spain,*, Guido MazzàbRicerca sul Sistema Energetico—RSE SpA, Milan 20134, Italy, Adrián Morales-TorresciPresas Risk Analysis, Valencia 46023, Spain, Jesica T. Castillo-RodríguezaInstitute for Water and Environmental Engineering, Universitat Politècnica de València, Valencia 46022, Spain

a r t i c l e i n f o

Article history:

Received 11 April 2016

Revised form 27 June 2016

Accepted 1 August 2016

Available online 19 September 2016

大坝

风险分析

计算方法

安全管理

水工结构

近年来，风险分析技术日渐成为大坝安全管理的有效工具。本文系统总结了由国际大坝委员会大坝分析和设计计算专家委员会主办的基准研讨会中与大坝风险分析主题相关的三方面研究成果。2011年，基准研讨会讨论了估算重力坝滑动破坏模式下的溃坝概率等问题；2013年，会议讨论了大坝风险分析中后果评估在计算方面所面临的挑战；2015年，会议对土石坝滑动和漫顶破坏的概率进行了分析。从这三次会议关于大坝风险分析数值计算的研究进展可以发现，对于大坝系统的风险分析，包括下游后果评价以及结构模型的不确定性，风险分析方法都是非常有用的工具。

© 2016 THE AUTHORS. Published by Elsevier LTD on behalf of Chinese Academy of Engineering and Higher Education Press Limited Company. This is an open access article under the CC BY-NC-ND license

(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1. 引言

对于可能给当地居民和环境造成潜在威胁的大坝结构开展安全水平的可靠评估，具有至关重要的意义，将对相关区域产生重大的经济影响和社会影响。

在坝工领域，目前人们已经普遍使用数值模型进行结构安全水平的定量评估，这主要归功于“国际大坝委员会(ICOLD)大坝分析和设计计算专家委员会”(下文简称“大坝分析和设计计算专家委员会”)所做的大量工作。然而，由于数学建模专家、大坝工程师和管理者之间在认识上存在较大分歧，将数值模型应用于实际工程问题曾经历过一段困难时期。数学建模专家是擅长开发计算机模型的信息系统专家，大坝工程师则是倾向于使用传统评估方法和基于其可靠经验的专业人员。大坝分析和设计计算专家委员会旨在弥合两者间的分歧，并促进计算机软件在大坝工程领域得到应用。1988年，该委员会被国际大坝委员会指定为临时特别委员会，并最终在2005年国际大坝委员会年会期间，正式成为国际大坝委员会的永久性专家委员会。

为指导和帮助大坝工程师正确使用计算机程序和数值模型，该专家委员会已经推进了广泛的基准计划。目前，已经成功举办了十三届基准研讨会，第一届于1991年在意大利贝加莫举办，上一届于2015年在瑞士洛桑举办。该专家委员会的各种技术目标主要包括：在实测大坝性状与模拟过程之间建立紧密的联系；发布用于教育目的的业内实践指南；改善用以解决与安全性相关的数学模型；评估用于优化设计、仪器监测、监控和安全/风险评估程序的计算机编程的潜在能力。2011—2015年，对于最后一个主题，陆续提出了三个与风险评估紧密相关的议题(见图1)，并对风险评估过程的不同阶段开展了大量的研究。本文将对基准研讨会的议题和所取得的主要成果进行详细的论述。

2. 2011年巴伦西亚研讨会：重力坝滑动破坏模式下的溃坝概率估算

2011年10月20—21日，第11届大坝数值分析基准研讨会在巴伦西亚召开。本次会议主题C的目的是确定80 m高重力坝沿坝基滑动失稳模式下库水位、安全系数和溃坝概率之间的关系。在对大坝和它的基础进行分析时采用了不同的模型以及可靠度分析技术，并公布了8个小组的计算成果[1]。在解决上述拟定问题时，所有参与者都按照以下步骤开展相同的工作。

2.1. 安全系数

首先，每个小组选择一个二维模型，计算(滑动破坏模式下)不同库水位的安全系数。所有参与者至少需要选择一种二维刚体极限平衡模型(LEM)。虽然更为成熟的、基于有限元分析的模型开发有了长足进展，但是刚体极限平衡模型仍被公认为是分析大坝安全的最常用方法[2]。在刚体极限平衡分析模型中，大坝与基础接触的有效面积能提供倾覆抵抗力矩，通过减少这一面积来模拟水平裂缝的演变过程。有两个研究小组在有限元分析模型中，借助变形体模型来评估裂缝的长度。研究人员采用不同的方法模拟水平裂缝，并计算排水有效和排水失效两种工况下的安全系数。对于排水有效这一工况的安全系数，各个小组得到的安全系数差异情况见图2。

图1.基准研讨会议题和风险分析各部分之间的联系。

如图2所示，在应用可靠度分析方法之前，不同方法得到的安全系数呈现出明显的差异。这种差异性主要是由于选定的假设和模型设置所引起的，另一个重要因素是确定安全系数，即使采用相同的刚体极限平衡模型和相同的强度参数，也不一定能得到相同的结果。

2.2. 摩擦角和凝聚力

各小组确定所选的随机变量(如摩擦角ϕ和凝聚力c)的分布特性。选择摩擦角(ϕ)或摩擦系数(tanϕ)为随机变量，会对计算结果产生一定的影响。根据计算结果来看，选择tanϕ为随机变量并假定其为正态概率密度函数(PDF)得到的失效概率，似乎比选择摩擦角(ϕ)为随机变量并假定其服从正态分布得到的失效概率更大一点。

另外，需要确定使用何种概率密度函数。本案例提供了大量的试验数据，以便使这一工作简化，但是在通常的案例中，即使有数据产生，其数值也很小。除了所提供的数据外，参与者还提出(或考虑)了几种分布函数，如正态分布、对数正态分布、瑞利分布和贝塔分布等。

在确定概率密度函数时，不仅需要考虑所选的分布函数的类型，还要考虑其适用性的物理含义。当使用无界概率密度函数，如正态分布时，其计算结果显示，对分布函数进行截断就成为分析过程的关键点，此时需要用工程经验来帮助确定概率密度函数截断所采用的最小值。

2.3. 溃坝概率

参与者使用至少一种二级可靠度分析方法，和一种三级方法——蒙特卡洛模拟法，来确定滑动破坏模式下重力坝的溃坝概率。关于这些可靠度分析方法的详细内容参见文献[3]。可靠度分析方法的类型也会对计算结果产生明显的影响。二级分析方法操作起来相对简单，如果所采用的变量数目较少，其用时也相对较短；而采用三级的蒙特卡洛模拟法得到的计算结果则更为精确，但计算时间较长，计算工作量也更大。在溃坝概率分析时，二级和三级可靠度分析方法经常与刚体极限平衡分析模型结合起来使用。总的说来，三级可靠度分析方法得到的溃坝概率比用二级分析方法得到的溃坝概率更低。

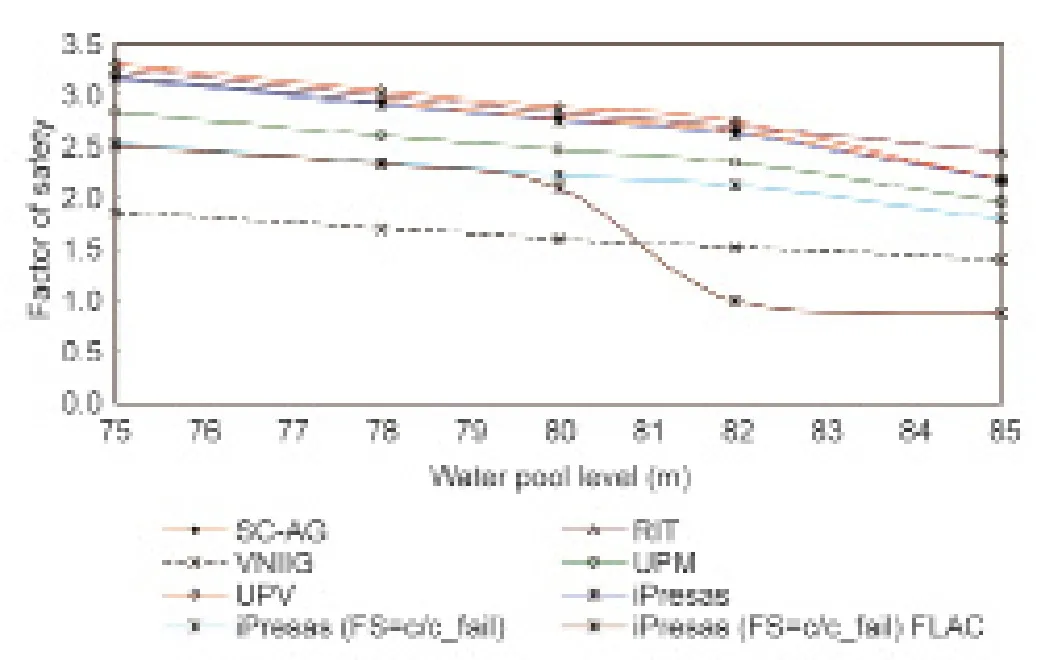
图2.在排水有效的情况下，参与者用不同方法得到的安全系数与库水位之间的关系。

2.4. 事件树模型

最后，许多小组综合考虑了两种排水条件下的结果，通过事件树模型将各单独的概率合并分析，获得总的溃坝概率。用三级可靠度分析方法得到的结果见图3。

从图3可看出，不同的参与者获得的计算结果差异显著。产生这一差异的主要原因在于设定二维模型和确定随机变量。比较刚体极限平衡模型和有限元模型使用三级的蒙特卡洛模拟法得到的计算结果可以发现，在排水有效的条件下，当库水位低于坝顶高程时，两种模型的计算结果基本一致；当库水位高于坝顶高程时，使用有限元模型得到的溃坝概率值接近于1，而刚体极限平衡模型的预测值则低于10–2，这是因为在刚体极限平衡分析模型中，线性应力分布假设处于“不安全”侧的原因。

综上所述，所有参与者的计算结果，为大坝分析中不确定性的主要来源开辟了新的讨论空间，如分析模型的类型、安全系数的确定和随机变量的统计分析等。总之，参数的不确定性仅是问题的一部分，而且在整个分析过程中其他不确定性因素也明显存在，需要进行更深入的研究来处理这些不确定性因素。

3. 2013年格拉茨研讨会：大坝风险评估中后果估计的计算挑战

2013年10月2—4日，第12届大坝数值分析基准研讨会在格拉茨召开。本次会议主题C “大坝风险分析中后果估计的计算挑战”(由Yazmin Seda-Sanabria、Enrique E. Matheu和 Timothy N. McPherson提出[4])的主要目的是确定当位于市区上游3.5 km处的土石坝发生溃坝时其存在的潜在后果。

组织者要求参与者自主选择用于解决问题的数值模拟类型和复杂程度，其中包括一维、二维和三维洪水模拟工具，人口风险(PAR)和生命损失(LOL)的估算技术，以及资产和后果评估模型等。在主题C中，需要解决对人类造成的威胁(如PAR和LOL)和对经济造成的直接影响问题。

会上介绍了8个参与者的计算成果，其完整论述见文献[4]，现基于以下几方面对这些结果进行比较。

图3.使用三级可靠度分析方法得到的破坏概率和库水位之间的关系。

3.1. 洪水特征

参与者采用了一系列模型，其中包括基于物理原理的溃坝模型(其中考虑了坝体材料信息)和基于以往大坝溃决案例的回归方程。模型、方法和参数的选择可以显著影响洪峰流量的时间和量值。计算结果表明，使用回归方程的模型比基于物理原理的模型洪峰来得更早。

此外，研究小组使用各种不同的技术来得到必要的洪水输出数据，以便于进行后果分析。大坝溃决水动力仿真结果取决于输入的数据组(如溃口流量、地形、糙率)和方法。参与者使用不同的方法估算糙率系数，结果却出现了较大差异。

各方案中的最大洪泛区面积为30～47 km2。但比较参与者的计算结果时发现(两两比较)，大多数方案都有较大的相似性。尽管各方案在洪泛区面积上存在相似性，但其溃坝洪水到达时间却不同，这主要取决于确定洪水到达时间所考虑的阈值(如洪水深度到达指定值的时间)。

3.2. 人口风险(PAR)

人口普查和土地利用数据由会议主题的编制者提供。不同参与者给出的洪泛区人口空间分布差异较大。其中，3位参与者为便于正确汇总洪灾人口普查区的受灾人口，把人口均匀分配在部分淹没的人口普查区内；另外3位参与者将人口重新分配到所提供的地块数据中；还有1位参与者将地块内的居住人口和工作人口也计算在内；最后1位参与者使用发达地区的不受外界干扰的程度来分配人口。

洪水深度低于2 m时，在风险人口方面，各方案呈现出一致的结果；但人口分布方面的这些差异导致风险人口数处于15 000～30 000人之间。另外，还发现各参与者在确定洪水的严重性方面也存在较大差异(如根据暴露人口数量或对建筑物的影响来确定洪水的严重性等)。

3.3. 生命损失(LOL)

大多数参与者对生命损失的估算结果基本类似，估计约有2000人死亡。但是，其中1位参与者提供的生命损失估算结果与其他参与者差异较大，其估算死亡人数达到4000人，这一差异主要是由于所确定的洪水严重程度不同而导致的。

3.4. 直接经济损失

由于在经济后果估算中使用的方法不同(如GDP对保险损失)，以及不同的资产价值假设，导致不同参与者给出的直接经济损失值差别较大，损失在4亿～26亿美元之间。

总的说来，此基准研讨会结果显示，水力学方面的结果相似；但是，各小组得出的洪峰到达时间不同。如策划者所述，这是由于溃口水位曲线的计算以及回归方程和基于物理原理的公式存在差异所导致的。洪峰深度最大差异产生的原因，可能是由于将不规则网格产生的结果转化成规则的网格输出所造成的。

所有参与小组都给出了相似的PAR估计结果，但在洪峰到达时间和洪水严重程度估计上却存在较大差异。经济后果分析也存在显著的差异，这主要是因为对直接影响的阐释和资产价值的估计不同。

总之，尽管有生命损失和经济后果估算的指导准则和引用文献(例如文献[5–7])，但由于使用的方法和定义以及参与者的假设范围较广，因此在溃坝后果估计中出现了某些方面的显著差异。需要强调的是，虽然存在这些差异，但生命损失和经济损失的结果仍然处于同一数量级。

4. 2015年洛桑研讨会：边坡失稳和漫顶诱发土石坝溃坝的概率

2015年9月9—11日，第13届基准会议在洛桑召开，会议主要讨论了土石坝溃坝的问题。虽然没有实测的抗力数据和水文数据，但我们从一个西班牙大坝的案例中得到启发，将重点放在考虑自然和认知的不确定性方面以计算出边坡失稳和漫顶破坏模式的易损性曲线，并使用这些曲线来计算年溃坝概率[8]，而参与者给出了3种不同的解决方案([9–11])。下文主要将这些解决方案与议题策划者给出的参考方案进行对比并展开分析。

策划方案是一座16 m高的均质土坝。近年来，该土坝的下游坝坡已出现局部失稳的问题，所以建议采用定量风险分析法来估算该坝的年溃坝概率。分析中主要考虑了两种溃坝模式——漫顶和大坝失稳。上述两种溃坝模式中，库水位被认为是导致溃坝的主要驱动力，下面从5个步骤展开讨论。

4.1. 失稳破坏模式的分析

为大坝下游边坡拟定一个边坡失稳的极限模型，并确定该模型主要的随机变量。这一步骤中，参与者使用了完全不同的边坡失稳分析方法，包括简单的极限平衡分析法和更全面的有限元分析法。此外，对稳定水力条件和瞬态水力条件这两种不同的水力条件进行了假设比较。

为了考虑自然和认知这两种不确定性，建议在摩尔–库仑破坏原则中采用摩擦角和凝聚力这两个随机变量，并向参与者提供了这些变量的主要统计参数。

4.2. 参考易损性曲线的计算

通过使用上一步骤中确定的随机变量的不确定性分布，计算坝坡失稳的参考易损性曲线(库水位与破坏概率之间的关系)。通过比较不同方法得到的易损性曲线(见图4)可以发现，尽管参与者都采用了具有相同分布特征和几何特征的随机变量，但却得出了不同的易损性曲线分布。这些结果表明，所做的假定和使用的模型都会对结果产生很大的影响。另外，蒙特卡洛模拟的次数也对参考易损性曲线的计算结果有显著影响。

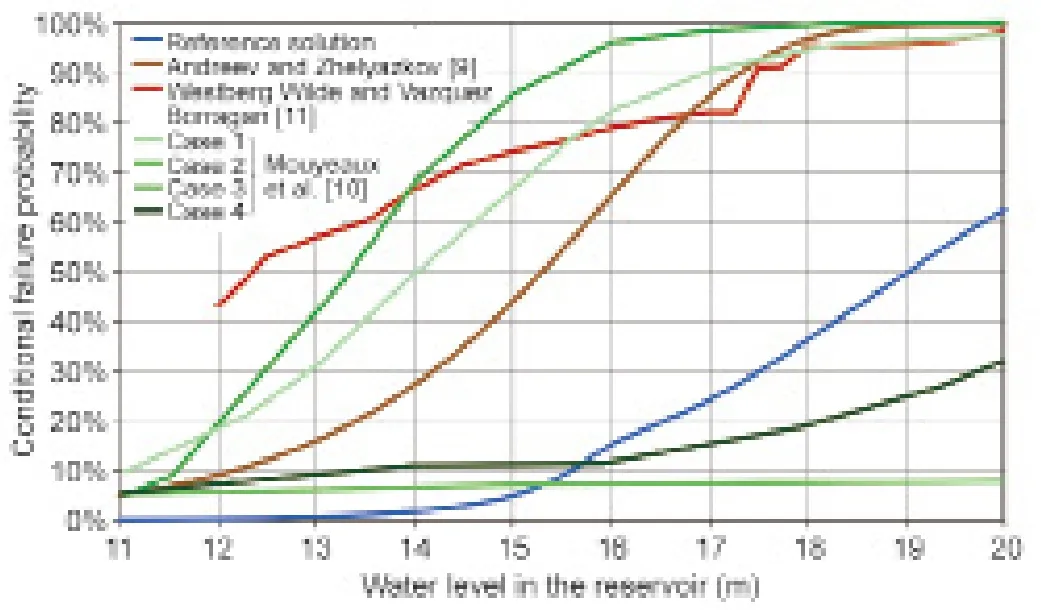
图4.参与者所计算的滑动易损性曲线对比。

在研讨会期间，有人强调水力假设尤其重要。在本案例中，按照稳定水力条件考虑可能会导致边坡抗力被低估。在建立数值模型的任何情形下都应注意所做的假设会对结果产生的影响。例如，两个参与者使用同一软件工具、相同的几何形状和相同的随机变量，却得到了极不相同的易损性曲线。

漫顶破坏模式的参考易损性曲线可以通过对数正态分布来直接确定，根据这些结果，所有参与者得出相同的结论——边坡失稳破坏模式明显比漫顶更值得关注。

从两种破坏模式的参考易损性曲线综合考虑，可以绘制出综合参考易损性曲线，代表该土坝在不同库水位下的结构性状。

采用常见因素调节技术[12]对所有方案进行两种破坏模式的综合分析。使用上限或下限，对该组合方法不会有很大的影响，其中边坡失稳破坏模式显然是主要的破坏模式，因为只有在概率极低的库水位条件下才会发生漫顶。

4.3. 库水位概率的计算

库水位概率的计算是为了获得库水位和年度超越概率(AEP)之间的关系。基于假设的洪水和水库数据，通过评估不同洪水事件中洪水在水库中的路径和底孔泄洪能力，对该曲线进行了估算。对不同的库水位，所有参与者都获得了相似的超越概率曲线。参与者全部使用了相同的洪水和水库数据，所用的洪水路径也非常简单，所以在4种解决方案中洪水路径的结果非常相似。

4.4. 计算溃坝概率和开展敏感性分析

使用前一阶段计算的曲线，再结合参考易损性曲线来计算参考破坏概率。通过比较可以发现，所获得的年溃坝概率结果有较大的差异，差异范围为1.8×10–1～4.1×10–3。这些差异主要是因为采用了不同的易损性曲线，说明用于分析该溃坝模式所作的假设很明显是调节的结果。所得到的年溃坝概率值较高，主要是因为修改了大坝的抗力和水文数据，以增加一定条件下的溃坝概率来减少样本数量。

4.5. 评估认知的不确定性

在这一阶段，使用各随机变量平均值的概率分布来确定认知的不确定性，这些分布被用于获得失稳破坏模式的一系列易损性曲线。漫顶破坏模式的系列易损性曲线是直接在该议题的谈论策划中确定的。最后，将这两个系列的易损性曲线进行组合，从而获得溃坝概率的轮廓线。仅有两位参与者做了这一阶段的工作(见图5)。这两条曲线的差异较大，与通过失稳模型所获得的易损性曲线差异一致。在两种解决方案中，两条溃坝概率的轮廓线表明，抗力参数分布中的小变化却可以造成易损性曲线的大变化，这恰恰说明了单独评估认知中不确定性的重要性。

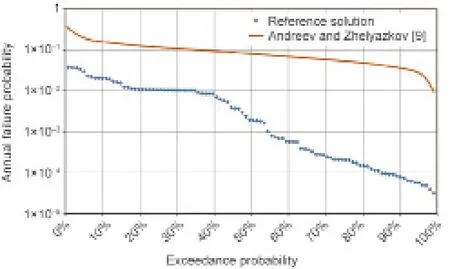
图5.参与者所计算破坏概率轮廓线的对比。

主要差异产生的原因是失稳破坏模式带入的易损性曲线有差异造成的。该对比说明即使采用相同的几何形状和抗力参数，只要所做的假设不同，就可获得极不相同的结果，尤其是水力条件假设具有极大的影响。因此，不确定性不仅来源于抗力参数，还有边坡失稳模型的选择和大坝的水力性状等。

目前已经证实，在对假定条件可能造成的影响进行分析时，风险分析是一个有效的工具。此外，还可以从获得的结果中看出该从何处着手来降低不确定性。因此，区分自然和认知不确定性是大坝安全管理中的岩土工程分析的基础工作。

5. 结语

目前已有用于风险评估的新技术，同时还能为大坝维护或修复决策提供相关的信息支持。2011年以来，国际大坝委员会一直致力于从计算角度来解决这个问题，还提供一些文献资料用于了解和关注在风险分析和标准设计技术(如事件频率、安全系数、溃坝参数等)中所作出的决策。

将此风险分析结合到专家委员会最近组织的三次基准研讨会中，为应用这些技术提供了多种方法，包括风险分析所涉及的三个组成部分：荷载、系统响应和影响。基准研讨会的高参与度以及会上所提出的大量解决问题的方案，足以显示大坝利益共同体对可靠度方法和风险分析在大坝安全性应用方面的关注。基准研讨会已经有效地促进了相关知识的交流与讨论。

计算方法的最新进展促进了风险分析技术的进一步开发，从简单的结构模型发展到复杂的数值计算程序和方法。计算方法仍然有改进提升的空间，如当数据收集并进行风险计算时如何适当解决认知的不确定性等问题。

基准研讨会表明，即使是相对简单和众所周知的工程问题与风险分析技术结合时，仍应按照工程判断来开展分析讨论，进而获得有意义的信息来开展大坝的安全管理工作。

基准研讨会的结果表明，当数值模型应用于大坝安全分析时，假设条件可以大幅度改变实验结果。因此，当给出结果时应明确阐述和解释所作的假设与结果之间的对应关系。从这层意义上来说，要对工程师日常设计实践中所作的假设而产生的影响开展分析，风险分析已经被证实是一个有用的工具，但也是最容易被忽略的。

下一步开展的工作包括：

(1) 开展认知不确定性的影响分析，可以更好地理解认知不确定性对负荷和阻力参数的风险结果所构成的影响。

(2) 采用多重风险分析方法开展分析风险。通过全面的方法来估计风险，包括所有潜在的风险(例如洪水、地震)及其相关性风险分析。

(3) 分析不同故障模式之间的相关性，可以理清现有故障机制间的相关性，以便在更好地描述风险的同时可以分析不同的假设(如假设用于共同的原因或者调节)所造成的影响。

(4) 为了更好地评估大坝溃坝的后果，包括警告和疏散的不确定的有效性，应对疏散人群产生的后果开展研究。

Acknowledgements

This paper was published with the support of the research project INICIA (Methodology for Assessing Investments on Water Cycle Infrastructures informed on Risk and Energy Efficiency Indicators, BIA2013-48157-C2-1-R, 2014–2016) funded by the Spanish Ministerio de Economia y Competitividad (Programa Estatal de Investigación, Desarrollo e Innovación Orientada a los Retos de la Sociedad).

Compliance with ethics guidelines

Ignacio Escuder-Bueno, Guido Mazzà, Adrián Morales-Torres, and Jesica T. Castillo-Rodríguez declare that they have no conflict of interest or financial conflicts to disclose.

[1] Altarejos-García L, Escuder-Bueno I, Serrano-Lombillo A. Theme C: estimation of the probability of failure of a gravity dam. In: Proceedings of 11th ICOLD Benchmark Workshop on Numerical Analysis of Dams; 2011 Oct 20—21; Valencia, Spain; 2011.

[2] Krounis A, Johansson F. The influence of correlation between cohesion and friction angle on the probability of failure for sliding of concrete dams. In: Escuder-Bueno I, Matheu E, Altarejos-García L, Castillo-Rodríguez JT, editors Risk analysis, dam safety, dam security and critical infrastructure management. Leiden: CRC Press; 2012. p. 75—80.

[3] Altarejos-García L, Escuder-Bueno I, Serrano-Lombillo A, de Membrillera-Ortuño MG. Methodology for estimating the probability of failure by sliding in concrete gravity dams in the context of risk analysis. Struct Saf 2012;36−37:1−13.

[4] Zenz G, Goldgruber M, editors. Proceedings of the ICOLD—12th International Benchmark Workshop on Numerical Analysis of Dams; 2013 Oct 2−4; Graz, Austria. Graz: Austrian National Committee on Large Dams; 2013.

[5] Merz B, Kreibich H, Schwarze R, Thieken AH. Review article “assessment of economic flood damage.” NHESS 2010;10(8):1697—724.

[6] US Department of Homeland Security. Dams sector: estimating economic consequences for dam failure scenarios. 2011.

[7] United States Bureau of Reclamation, United States Army Corps of Engineers. Best practices in dam and levee safety risk analysis. 2015.

[8] Morales-Torres A, Escuder-Bueno I. Theme B: problem formulation: probability of failure of an embankment dam due to slope instability and overtopping. In: Russell Michael G, Marc B, Pedro M, Laurent M, Anton S, editors Proceedings of the 13th ICOLD International Benchmark Workshop on Numerical Analysis of Dams; 2015 Sep 9—11; Lausanne, Switzerland; 2015.

[9] Andreev S, Zhelyazkov AZ. Probability of failure of an embankment dam due to slope instability and overtopping: first order second moment method for assessment of uncertainty. In: Russell Michael G, Marc B, Pedro M, Laurent M, Anton S, editors Proceedings of the 13th ICOLD International Benchmark Workshop on Numerical Analysis of Dams; 2015 Sep 9—11; Lausanne, Switzerland; 2015.

[10] Mouyeaux A, Carvajal C, Peyras L, Bressolette P, Breul P, Bacconnet C. Probability of failure of an embankment dam due to slope instability and overtopping. In: Russell Michael G, Marc B, Pedro M, Laurent M, Anton S, editors Proceedings of the 13th ICOLD International Benchmark Workshop on Numerical Analysis of Dams; 2015 Sep 9—11; Lausanne, Switzerland; 2015.

[11] Westberg Wilde M, Vazquez Borragan A. Theme B: system approach to probability of failure of an embankment dam. In: Russell Michael G, Marc B, Pedro M, Laurent M, Anton S, editors Proceedings of the 13th ICOLD International Benchmark Workshop on Numerical Analysis of Dams; 2015 Sep 9—11; Lausanne, Switzerland; 2015.

[12] Spanish Committee on Large Dams. Technical guide on the operation of dams and reservoirs vol. 1: risk analysis applied to security management of dams and reservoirs. Madrid: Exce Consulting Group; 2012. Spanish.

* Corresponding author.

E-mail address: iescuder@hma.upv.es

2095-8099/© 2016 THE AUTHORS. Published by Elsevier LTD on behalf of Chinese Academy of Engineering and Higher Education Press Limited Company.

This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).

英文原文: Engineering 2016, 2(3): 319—324

Ignacio Escuder-Bueno, Guido Mazzà, Adrián Morales-Torres, Jesica T. Castillo-Rodríguez. Computational Aspects of Dam Risk Analysis: Findings and Challenges. Engineering, http://dx.doi.org/10.1016/J.ENG.2016.03.005