客运专线大跨度T构墩梁固结处优化措施研究

杨银庆

(铁道第三勘察设计院集团有限公司， 天津 300142)

客运专线大跨度T构墩梁固结处优化措施研究

杨银庆

(铁道第三勘察设计院集团有限公司， 天津 300142)

大跨度T构桥墩梁固结区域是设计的关键部位，需确定合理的墩梁固结构造措施，以保证此处结构受力的合理性。但墩梁固结处的局部应力状态及构造措施有待进一步深入研究。文章以长昆客运专线龙溪大桥70 mT构为依托，采用有限元程序对墩梁固结处进行了精细化模拟。在对局部应力分析结果的基础上，对墩梁固结的细节提出了墩梁固结下腋处设倒角、墩顶设帮宽和箱体内设倒角3处优化措施，并对优化前后的应力进行了对照分析。结构优化后，主拉、主压应力峰值消减效果较好，主拉应力最大可下降64.78%，主压应力可下降14.71%。经研究表明，墩梁固结处局部应力分析方法可行，措施优化有效，对类似工程有借鉴意义。

T构； 墩梁固结； 局部应力； 优化措施

1 概述

对于大跨度预应力混凝土T型刚构桥梁，墩梁固结区域是设计的关键部位，此处结构构造和应力分布都比较复杂，需选择合理的墩梁固结构造措施以保证此处结构受力的合理性。这就需要在全桥总体分析的基础上，对不同构造情况下该区域应力分布情况进行详细的空间对比分析。本文依托长昆客运专线龙溪大桥进行相关研究分析，该桥采用无砟轨道(70+70)m预应力混凝土T构，主梁全长141.5 m，计算跨度为(70+70)m，边跨设置12.25 m等高段，截面采用单箱单室、变截面直腹板形式箱梁，中支点处梁高8.0 m，边跨等高段梁高4.0 m，顶宽12.0 m，底宽7.0 m。本文着重对墩梁固结处的局部应力集中点进行结构优化设计，通过对结构优化前、优化后的对比分析，得出结构优化措施的效果及可行性。

2 墩梁固结处局部应力分析

2.1 计算方法

本文先利用通用有限元程序MIDAS对全桥进行各个阶段的内力计算，再根据圣维南原理将梁端内力、静力等效地加在局部模型的截断处，计算可反映局部受力的应力分布情况。根据圣维南原理，墩梁固结区的应力分布只与其附近区域的受力状态有关，根据工程经验，一般取2.5倍梁高范围进行计算。在墩梁固结区沿纵向截取42 m、沿着墩身截取20.5 m进行研究，可满足以上要求。

计算中采用的基本假定为：

(1)小变形假设。

(2)不考虑结构材料的非线性，将结构视为均质弹性体，以弹性模量和泊松比表示结构的材料特性。

(3)不考虑几何非线性效应。

2.2 建立有限元模型

如图1有限元模型采用了Solid45实体单元和Link8杆单元分别模拟混凝土和预应力刚束。在进行ANSYS建模时采用了以下简化处理方法：

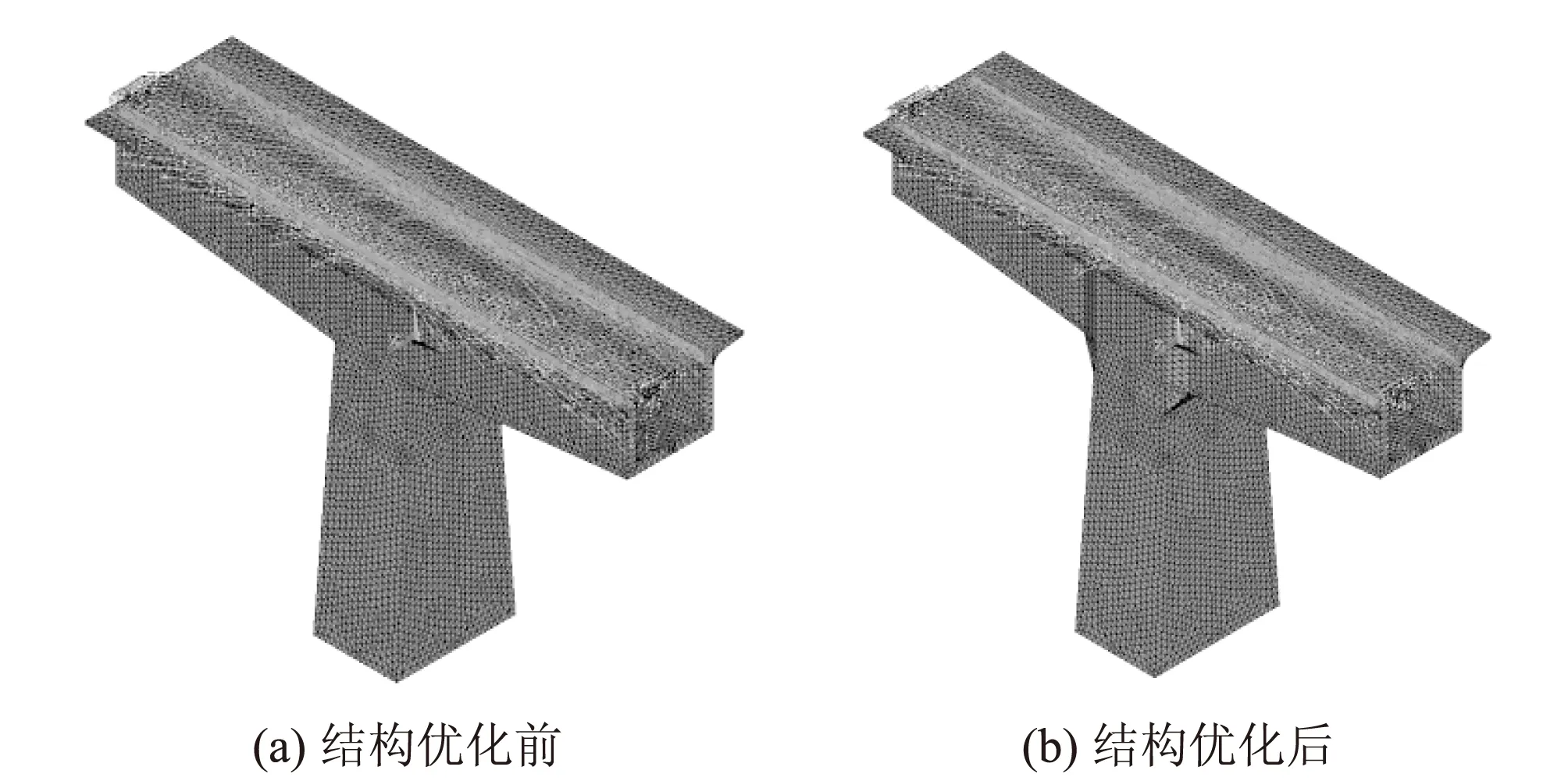
图1 ANSYS局部模型单元划分图

(1)固结全部墩身最底部截面节点。

(2)将梁截面重心处的节点与该截面处所有节点进行刚接，外力施加于重心节点处。

(3)采用节点耦合技术实现预应力钢束单元与混凝土单元之间的连接。此方法可以避免对混凝土进行切割从而形成预应力钢束位置的繁琐步骤，同时能够满足墩梁固结处研究的精度要求。

(4)对有限元模型中预应力的模拟采用单元降温的方法，降温值T=张拉力P/(线膨胀系数α×弹性模量E×钢束面积A)。计算张拉应力采用整体模型中的平均有效预应力，预应力钢束线膨胀系数为1.2e-5。

2.3 荷载及工况

荷载考虑自重、二恒、预应力、收缩徐变以及列车荷载，计算对如下3个工况进行分析：

工况1：最大悬臂阶段，即结构合龙前；

工况2：运营十年后恒载(考虑自重、二恒、预应力和收缩徐变)；

工况3：运营十年后恒载(考虑自重、二恒、预应力和收缩徐变)+双车道双线列车活载。

对于工况2和工况3，由于结构为超静定体系，预应力会对结构产生初内力和次内力。由于初内力已经通过模型中建立的预应力钢束单元，对其实施降温实现，故对局部模型梁端施加的恒载需扣除钢束初内力。

对于工况3中的双线列车活载，利用整体MIDAS模型的移动荷载追踪器功能，计算出墩顶梁截面处弯矩最大情况(或梁顶正应力最大)下的列车布置工况，将此工况作为静载加载于整体模型上，从而得出双线列车活载的梁端内力。

从力的平衡角度，局部模型中不仅需要施加梁端外力，而且需施加自重、二恒及列车活载分布力，只有考虑了这些分布力，才能使局部模型与整体模型的受力完全吻合。其中自重通过ANSYS中设定重力加速度来实现，二恒及列车活载分布力通过面荷载施加如图1所示，各荷载工况下梁端荷载，如表1所示。

图2 MIDAS整体模型中的双车道活载

2.4 墩梁固结优化措施

墩梁固结处结构构造，如图3所示。图中阴影部分为结构优化措施，共分为3处：墩梁固结下腋处设倒角、墩顶设帮宽、箱体内设倒角。

3 固结措施优化效果分析

3.1 墩梁固结处结构优化前计算结果

墩梁固结构造措施优化前后，工况2作用下的应力云图对照如图4～图6所示。可以看出，措施优化前后其应力分布规律基本一致。

表1 各荷载工况下梁端荷载

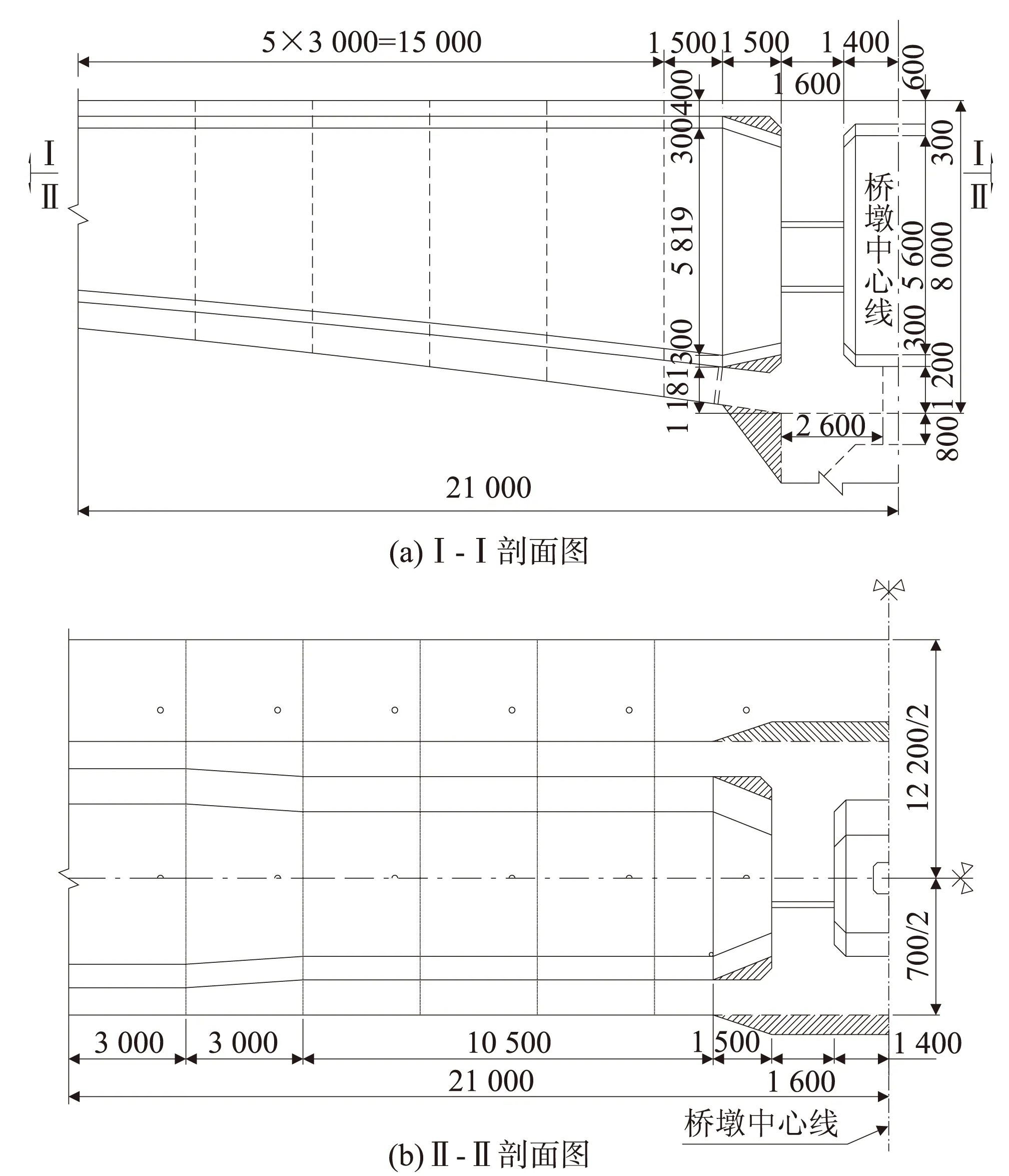
图3 墩梁固结措施图(mm)

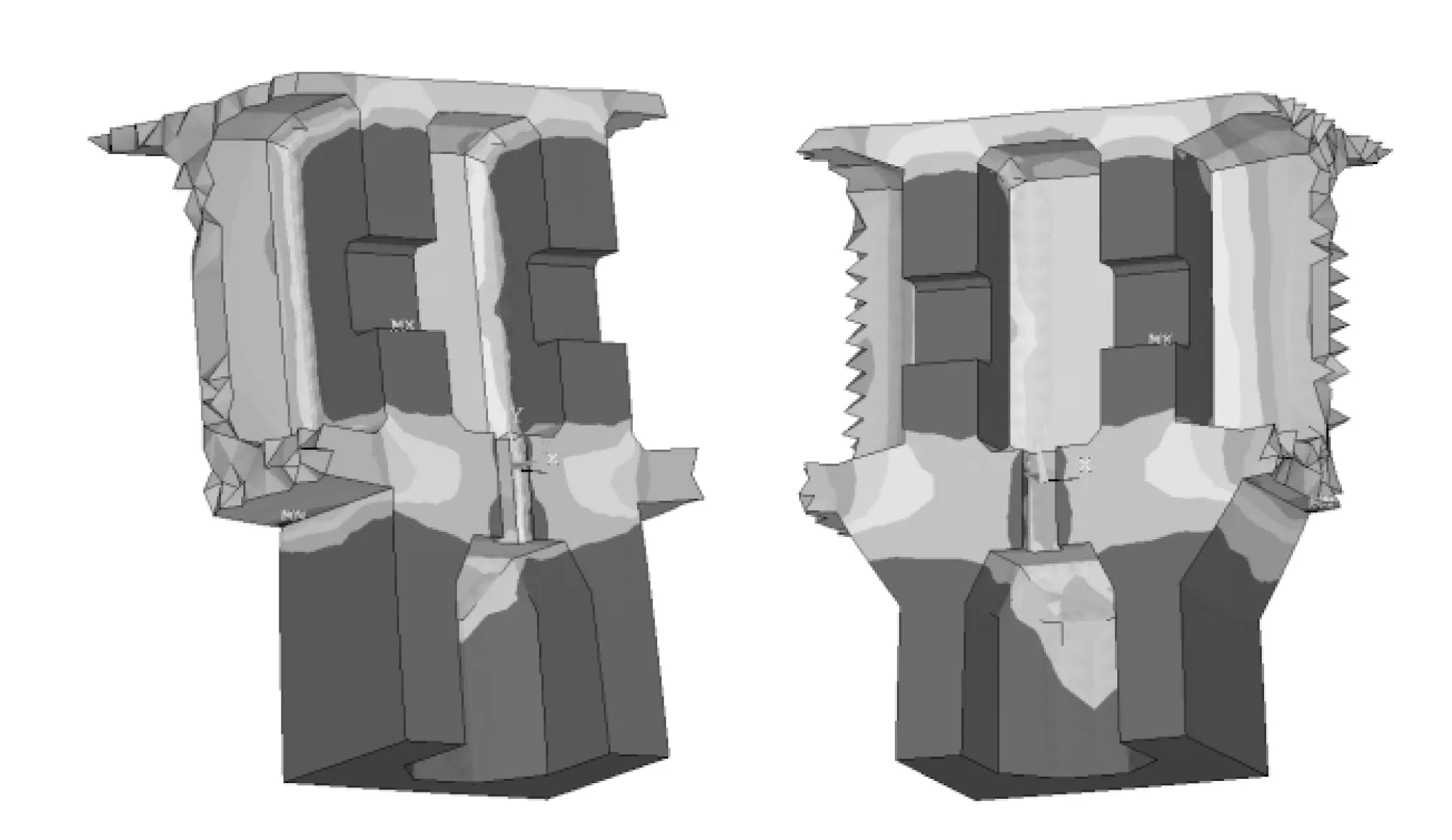
图4 工况2作用下混凝土σx应力图优化前后对照(Pa)

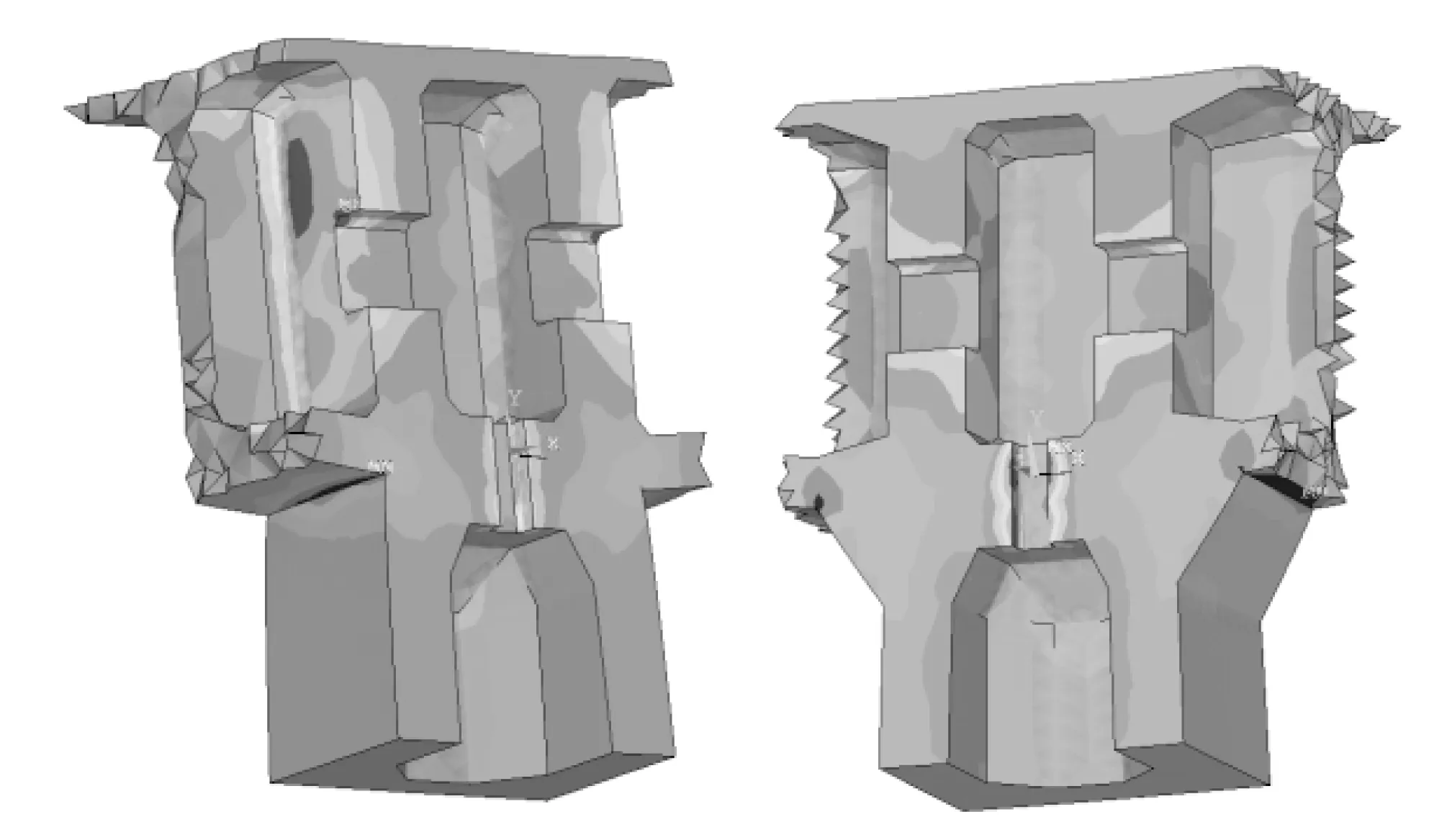
图5 工况2作用下混凝土σ1应力图优化前后对照(Pa)

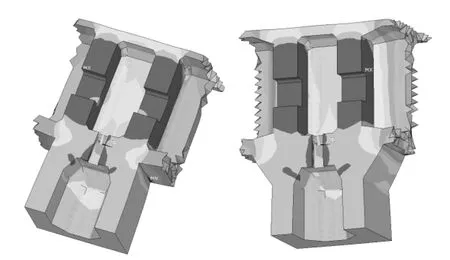
图6 工况2作用下混凝土σ3应力云图优化前后对照(Pa)

结构优化前，最大压应力出现在墩梁固结下腋处，工况1、工况2、工况3作用下分别为-11.7 MPa、-12.4 MPa、-14.3 MPa，满足规范要求的16.8 MPa最大主拉应力σ1出现在横隔板过人洞处，3种工况下其值分别为2.36 MPa、2.24 MPa、2.17 MPa。最大主压应力σ3位于墩梁固结下腋处，3种工况下其值分别为-13.8 MPa、-14.7 MPa、-17.0 MPa，小于主压应力限值20.1 MPa，系明显的应力集中现象。

3.2 墩梁固结处结构优化后计算结果

结构优化后，主要应力分布规律没有变化，但是各项应力幅值均都有所下降。从正应力σx图中可以看出，在墩梁固结处最大压应力依然出现在墩梁固结下腋处，数值有所下降，工况1、工况2、工况3作用下分别下降为-10.9 MPa(下降了6.84%)、-11.5 MPa(下降了7.26%)、-13.2 MPa(下降了7.69%)。

横隔板过人洞处最大主拉应力σ1大幅下降，3种工况下其值分别下降至1.08 MPa(下降了54.24%)、0.789 MPa(下降了64.78%)、0.854 MPa(下降了60.65%)。最大主拉应力σ1位置有变化，出现在墩顶过人洞处，其值分别为1.68 MPa、1.72 MPa、1.90 MPa。最大主压应力σ3依然位于墩梁固结下腋处，其值分别下降至-11.9 MPa(下降了13.77%)、-12.6 MPa(下降了14.29%)、-14.5 MPa(下降了14.71%)。

3.3 固结措施优化效果分析

结构优化前后计算结果对比如表2所示。从表2中可以得出，结构优化措施对横隔板过人洞处主拉应力影响最大，最大可下降64.78%； 对墩梁固结下腋处的主压应力可下降至14.71%，对墩梁固结下腋处正压应力影响可达到7.69%。对于具体结构的抗裂设计，一般斜截面抗裂计算要求严于正截面抗裂，主拉、主压应力是设计者控制的主要指标。由于本设计的固结优化措施对主拉、主压应力峰值消减效果较好，对结构的抗裂设计非常有利。因此本文对墩梁固结处的构造优化措施是有效合理的。

表2 结构优化前后计算结果对比表(MPa)

4 主要结论

(1) 3种工况作用下的结构优化前、优化后各工况应力分布规律基本一致。结构优化前后，最大正应力及主压应力均出现在墩梁固结下腋处，没有变化。而最大拉应力位置有变化，由梁横隔板过人洞移至墩顶过人洞处。

(2) 结构优化前，最大主拉应力σ1出现在横隔板过人洞处，3种工况下其值分别为2.36 MPa、2.24 MPa、2.17 MPa，超出主拉应力限值2.17 MPa。结构优化后则分别降低为1.08 MPa、0.789 MPa、0.854 MPa，小于主拉应力2.17 MPa，满足了规范要求。

(3) 结构优化措施对横隔板过人洞处主拉应力影响最大，最大可下降64.78%；对墩梁固结下腋处的主压应力可下降至14.71%，对墩梁固结下腋处正压应力影响可达到7.69%。结构优化后，主拉、主压应力峰值消减效果较好，对结构的抗裂设计非常有利。因此，本文对该T构墩梁固结措施的优化合理，对类似工程有借鉴意义。

[1] 刘作霖，徐兴玉.预应力T型刚构式桥[M]．北京：人民交通出版社，1982． LlU Zuolin，XU Xingyu. Prestressed Concrete T-Frame Bridges[M]．Beijing：ChinaCommunication Press，1982．

[2] 马保林．高墩大跨连续刚构桥[M]．北京：人民交通出版社，2001． MA Baolin．High Pier and Long Span Continuous Rigid-Frame Bridges[M]．Beijing: China Communication Press，2001．

[3] 饶少臣.大跨高墩T构铁路桥设计研究[J].铁道标准设计，2005，21(11)：52-56. RAO Shaochen. Design Research on High Pier and Long Span T-Frame Railway Bridge [J]. Railway Standard Design, 2005，21(11)：52-56.

[4] 毕玉琢．复杂山区铁路桥梁设计-宜万铁路桥梁设计介绍[J]．铁道标准设计，2005,21(11)：48-52. BI Yuzhuo．Introduction to Design of Bridges on Yichang to Wanzhou Railway in Complex Mountain Region [J]．Railway Standard Design，2005，21(11)：48-52．

[5] 吴昌期，李永铎．T型刚构桥[M]．北京：人民交通出版社，1981． WU Changqi, LI Yongduo．T-Frame Bridges[M]．Beijing：China Communication Press，1981．

[6] 江见鲸，陆新征，叶列平．混凝土结构有限元分析[M]．北京：清华大学出版社，2005． JIANG Jianjing，LU Xinzheng，YE Lieping．Finite Element Analysis of Concrete Structure[M]．Beijing: Tsinghua University Press，2005.

[7] TB 10621-2014高速铁路设计规范[S]. TB 10621-2014Code for Design of High Speed Railway[S].

[8] TB 10002.1-2005 铁路桥涵设计基本规范[S]. TB 10002.1-2005 Code for Design on Railway Bridge and Culvert[S].

[9] TB 10002.3-2005 铁路桥涵钢筋混凝土和预应力混凝土结构设计规范[S]. TB 10002.3-2005 Code for Design on Reinforced and Prestressed Concrete Structures of Railway Bridge and Culvert [S].

[10]TB 10005-2010 铁路混凝土结构耐久性设计规范[S]. TB 10005-2010 Code for Design of Durability of Railway Concrete Structure [S].

Study on Optimization Measures for Consolidation of Large Span T-Frame Pier Beam on Passenger Dedicated Line

YANG Yinqing

(The Third Railway Survey and Design InstituteGroup Corporation,Tianjin 300142,China)

Large span T-frame rigid bridge pier beam consolidation region is a key part of the design, the reasonable pier beam structure measures are necessary to ensure the rationality of the structure stress. But at the local pier beam consolidation, stress state and structural measures need to be further studied. In this paper, elaborate simulation of the pier beam consolidation by using finite element program is based on 70 m T-frame Longxi bridge on Changsha-Kunming passenger dedicated line. Based on the analysis results of the local stress, three optimization measures including pier beam consolidation axils set with chamfer, pier top design widen and chamfer set within box are proposed for the pier beam consolidation. And the stress before and after optimization are analyzed. After structure optimization, the main tension, the main pressure stress peak reduction effect is good, the main tensile stress can be reduced by 64.78%, and the main pressure stress can be reduced by 14.71%. The research shows that the local stress analysis method is feasible and effective, and it can be used as a reference for similar projects.

T-frame; pier beam consolidation; local stress; optimization measures

2016-03-31

杨银庆(1982-)，男，工程师。

1674—8247(2016)03—0087—04

U441+.5

A