基于大型数据集的聚类算法研究

杜淑颖

摘要：就精确系数不算太严格的情况而言，针对各种大型数据集，通过对比各种聚类算法，提出了一种部分优先聚类算法。然后在此基础之上分析研究聚类成员的产生过程与聚类融合方式，通过设计共识函数并利用加权方式确定类中心，在部分优先聚类算法的基础上进行聚类融合，从而使算法的计算准度加以提升。通过不断的实验，我们可以感受到优化之后算法的显著优势，这不仅体现在其可靠性，同时在其稳定性以及扩展性、鲁棒性等方面都得到了很好的展现。

关键词：部分优先聚类算法；聚类融合；效率；精度

中图分类号：TP393

文献标识码：A

DOI： 10.3969/j.issn.1003-6970.2016.01.030

0 引言

针对大型的数据来说，过去的聚类手段存在下面两个关键的不足。首先就是其数据集不够稳定，与低维相比，高维的分布更加广泛，这往往会出现数据之间等距的现象，通常而言，我们会按照距离来展开聚类工作，这样意味着高维数据集的构建难度进一步加大；其次，就高维数据集而言，其内在的属性往往没有直接的联系，所以基本上在所有维中存在类的概率为0。

1 部分优先聚类算法（Partial PriorityAlgorithm PPA）

就引言中的问题展开研究，进而提出部分优先算法，首先将第一类从原始数据中分离出来，删除第一类数据后，再分离形成第二类，反复循环下去，我们会发现其计算速度非常快，但是不满足使用的准确度要求，这种算法十分适用于准确度要求不是十分严格的数据集的计算。针对其准确度不足的情况，我们结合使用了加权的方法来确定类中心，以此来提升其稳定性与典型程度，这对于聚类的稳定性、延伸性以及时效性都是十分有利的。

1.1 概念定义

1.r-邻域：其中心是某一个数据点，半径用小写字母r表示。

2.典型样本p：其定义就是如果样本集A内部数据的r-邻域里存在有最基本的Minpts（密度阀值）个数据，那么该样本就叫做典型样本。

3.典型点C：p中全部数据的平均值为典型点，

其中p中样本的数量用|p|表示。

4.类中心：即样本中全部数值的平均值。

1.2 部分优先算法的设计案例

1.选择某一个数据集，然后随机抽取其中的一个样本A，确定A典型与否。任取样本中的某一个初始值，设置好固定的r与MinDts。然后以该点作为圆心，若Minpts的数值比r-邻域内的数据量小，那么就可以确定样本A具有代表性；

2.如果A具有很好的代表性，即确定其典型性，那么我们可以利用公式（1）求解出C₁，其中C₁是样本的典型点，也就是样本的中心；

3.如果A不具有代表性，即不具典型性质，那么可以重新进行第一个环节，一直到发现典型样本为止；

4.样本的中心聚类用C₁表示，利用公式

求解出C1与样本A中各对象的间距；

5.假如C₁与指定对象x_i两者的间距没有大于或等于，，那么我们将此对象合并进A内，反之，获取C₁和其他对象X_i+l两两之间的间距，完成A内包含的全部对象。

该算法的流程图见图1：

1.3 PPA的优势

1.旨在有效加强典型范例和相应的典型点的计算速度，此算法放弃选取数据集全部内容而是借助于随机挑选的方式从而获得典型样本，与此同时典型点的分析过程仅出现1次。

2.旨在增强典型点的代表水平，增加r-邻域中的数据密度，此计算方法制定典型样本数值的平均数为典型点，另一方面此点也能够被当作聚类中心。

3.旨在下调旧有数据集的繁琐程度，此算法在完成1个类之后，会把此类的数值从旧有合集内删除以避免重复。

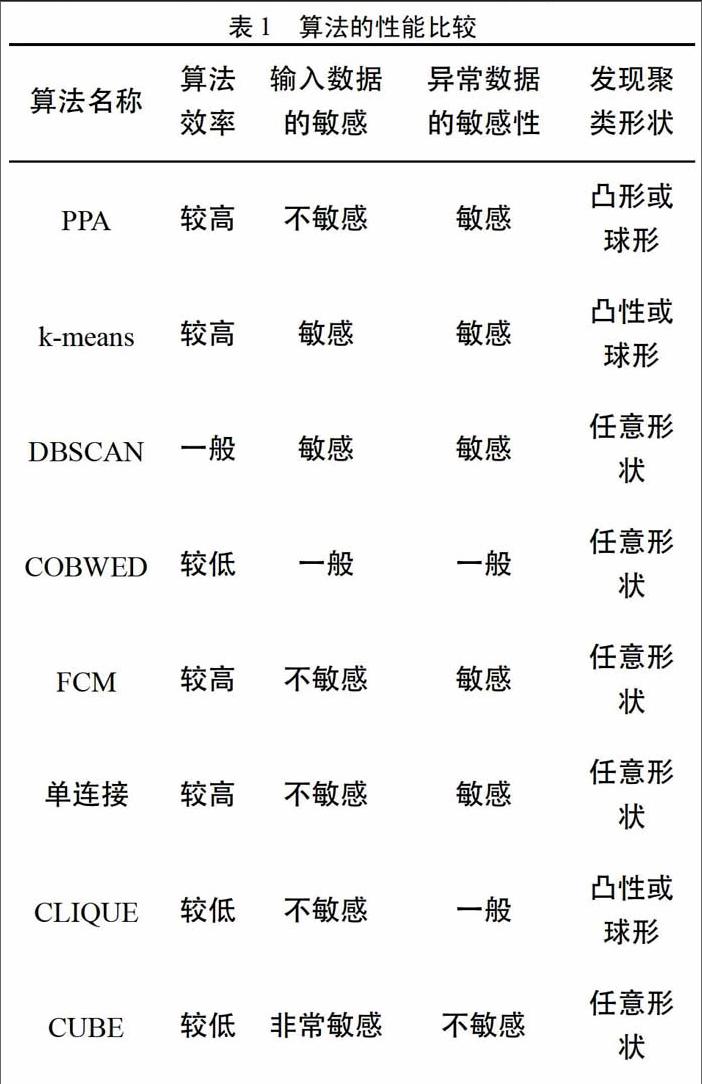
面对数值的排列PPA并不具备敏感性，这就会使PPA面向球形以及凸形集合时的分析速度更快。与此同时，PPA在样本平均数值处获得典型样本，所以在处理异常数据情况上相对更为敏感，评估异常点相对更为准确。PPA于聚类环节精简了旧有的合集，大幅度下调了旧有合集的繁琐性，因此我们不难发现其于功效上具备较大优势。PPA的分析能力、输入数据的敏感程度、面向异常数据的敏感程度、察觉聚类形状等方面和K-means clustering algorithm、DBSCANclustering algorithm. COBWEB clustering algorithm_FCM clustering algorithm、单连接聚类算法、CLIQUEclustering algorithm. CUBE clustering algorithm等模型开展比对，得出的相关结论详情见表1。

2 面向大型数据集的PPA的聚类融合

2.1 聚类融合基本思想

聚类融合（clustering ensemble，CE）旨在于消除单词聚类（word clustering）的较大波动性，把合集映射为数据点的相似度随之求出融合的划分，面向合集的归类途径为借助于1种算法中的多项参数或是多项算法，聚类成员的产生详情见图2。

CE的核心理念：假定存在n项数据点x={X₁，x₂，…，x_n}，面向x开展H次聚类求出H项聚类，π={π₁，π₂，…，π_n}，在此之中π_k（k=l，2，…，H）是第k次求解数据。假定存在共识函数r，详情见图3。

共识函数（consensus function，CF，也称为一致性函数）的定义标准为只要可以将需要聚类的所有聚类成员借助于其一标准完成融合过程，以共协矩阵（Co-association matrix）为例，相应的功能为评价数据内部的关联性，函数方程详见（3）：

聚类算法总次数H

接下来我们面向前面获得的H项结果展开融合，求出所需的聚类结果π'。聚类融合的详情情况见图4。

2.2 聚类融合算法的设计

我们假设一数据合集X={X₁，x₂，…，x_n}，

x_i={X_i1，x_i2，…，x_in}，借助于PPA算法把它进行归纳，PPA算法的特征为所有划分行为均会先出现第1个类，随后采取融合的途径得到所需的第1个类。第1次归纳总结一直到第r次归纳总结的第1个类为{C₁₁，C_{12，…，C1r}}， 相关的类中心则是{

}，旨在确保所有划分行为出现的第1个类存在差异，算法设计借助于改变数据的输入顺序从而达到目的。

融合方式定义为：借助于加权的方法从而求出第1类的类中心，此类中心的权重需要借助于此类中的全部数据量和每类数据量之和的比例而获得。

为类C..所含的数据量，V₁定义成所需的第1个类的类中心。随着v₁的求出，再确定空集T₁，将V赋予Z作为类中心开始聚类，假设存在阀值r，利用PPA算法的第5环节，求出的T₁即是所需出现的第1个类。于所有划分行为中把正包括的数值剔除，从而有效下调数据的繁琐性。

按照上述步骤获得剩余的k-l个类。由于V_i（i=l，2，…，k存在的典型性，所以出现T₁，T₂，…，T_k之后，余在旧有合集内的数据接近于0，算法设计将余下数值平分成k份，再依次移到T₁，T₂，…，T_k中，函数（5）即是所有类中心的算法函数，各类产生的详情见图5。

2.3 聚类融合算法的优势

1.旨在让类中心的代表水平以及相应的典型程度更为突出，分析归类更为精确，类中心借助于加权的方法从而实现此目的，借助于公式（5）获得所有类中心。

2.旨在增加计算性能，采用的类中心让原有数据集的内容极限精简。

3.旨在下调数据集的复杂程度，于归类期间把已完成分类的部分从原有数据集内剔除。

3 算法测试结果分析

采取9组从UCI Machine Learning Repo sitory合集中获得的数据（Size<2*104），各为Fertility，CarEvaluation， Abalon. Artificial Characters. ISOLET，Callt2 Building People Counts （CBPC）. Gas SensorArray Drift Dataset （GSADD）， p53 Mutants， LetterRecognition详细参数见表2，为验证算法是否具有稳定性，同时测试其可行性，面向表2囊括的9组合集分别开展5次PPA以及基于PPA的聚类融合算法，求解获得平均时间值、精度值和方差值。

按照表3以及图6中的内容，我们不难发现PPA算法和基于PPA的聚类融合（EPPA）算法相比较，PPA的运算效率更高一些，然而于精度层面开展比较，则是EPPA更胜一筹。按照获得的实验结果中的方差开展对比，我们发现PPA的鲁棒性更胜一筹。按照表4以及图7中的内容，我们能够得出结论：EPPA于处理大型数据过程中的抗外界干扰能力和其可靠性均具有显著强势。

根据获得的实验结果我们发现PPA以及EPPA容易受处理的数据量的多少以及维数大小的作用，于17，000数据处出现转折情况，与此之前要更平稳，之后就出现时间增加过快的现象。于精度层次上考虑，数据集超过6，000的情况下EPPA开始稳定，能够得出结论：EPPA的稳定性和可靠程度较高，面向未知数据集的计算上存在着巨大的潜力。

4 结论

本研究将常见的聚类算法开展一定程度上的优化，得到部分优先聚类算法，增强了算法的处理能力，提高其效率，然而于精度层次上考量，其可靠性仍然有待于后续优化，本研究于部分优先聚类算法的基础上开展了聚类融合，避免了此算法缺乏精度的缺点，增强其算法精度，使其于可扩展程度、鲁棒性、可靠程度等方面均有着传统聚类算法无法匹敌的优势，对于大型数据集的计算具有举足轻重的作用。