基于百度地图的改进的K—means算法研究
2016-03-08杨婷婷王雪梅
杨婷婷++王雪梅


摘要:聚类分析在科研和商业应用中都有着非常重要的应用,K-means算法是聚类方法中常用的一种划分方法。随着数据量的增加,K-means算法的局限性日益突出。在百度地图的各种坐标体系下,提出一种改进的基于网格的K-means算法,用新的方法确定k值以及K个初始质心。相对于传统的K-means算法,该算法在一定程度上减少了因采用误差平方和准则函数而出现较大的聚类簇分割开的情况,仿真实验结果表明:改进后的K-means算法优于原始算法,并且稳定性更好。
关键词:聚类;K-means算法;百度地图;稳定性
中图分类号:TP3-0
文献标识码:A
DOI: 10.3969/j.issn.1003-6970.2016.01.018
0 引言
数据挖掘即是从大量的、不完全的、有噪音的、模糊的、随机的实际应用数据中,发现并提取隐含在其中未知的、可信的、有用的模式的过程。目前,数据挖掘已广泛应用于大中型企业、商业、银行、保险等领域,成为未来3-5年内对工业有重大影响的关键技术之一。聚类是数据挖掘中的一类重要技术,是分析数据并从中发现有用信息的一种有效手段。由聚类所生成的簇是一组数据对象的集合,这些对象与同一簇中的对象彼此相似,与其他簇的对象相异。聚类算法有划分聚类算法、层次聚类算法、基于密度的聚类算法、基于网格的聚类算法、模糊聚类算法、子空间聚类算法。其中,K-me ans算法属于聚类方法中一种基本的划分方法,传统的K-means算法是输入聚类个数k,以及包含n个数据对象的数据库,输出满足方差最小标准的k个聚类。
如今,020如火如荼,移动地图一直被当作是020的重要入口之一,移动地图本身就是最该挖掘的宝藏,在如今的技术条件下,地图服务完全可以扩展成索引真实世界的关键按钮,成为连接所有020服务的平台。而地图中定位和导航的最终目的大多都会指向某种生活服务,那就是POI,它是“Pointlnterest”的缩写,每个POI包含名称、类别、经纬度等信息,我们在地图上看到xx商店、xx饭店的提示,就是POI数据。而市场份额占7成的百度,拥有最集中的用户场景需求,而且百度地图上的POI数据现在已经是行业内最多的,高德次之。随着地图上POI点数量的不断扩大,于是,在地图上展示过多的POI点信息会显得杂乱无章甚至出现覆盖现象,使得地图的可用性下降,不能很好的服务于群众。因此,基于百度地图的POI聚合也有更深远的研究意义。
本课题在020的发展背景下,在之前的各种聚类算法研究基础上,提出了基于百度地图的改进的K-means算法,利用地图特有的坐标体系,结合传统的K-means算法,提出一种改进的基于网格的K-means算法。该算法在POI聚合以及其他的聚合应用上有深远的研究意义。
l 现有K-means算法思想
1.1 K-means算法的基本思想概述
K-means算法是硬聚类算法,是典型的基于原型的目标函数聚类方法的代表,它是数据点到原型的某种距离作为优化的目标函数,利用函数求极值得方法得到迭代运算的调整规则。K-means算法以欧式距离作为相似度测度,它是求对应某一初始聚类中心向量V最优分类,使得评价指标J最小。算法采用误差平方和准则函数作为聚类准则函数。
1.1.1 K-means算法工作原理
K-means算法以K为参数,把n个对象分为K个簇,以使簇内具有较高的相似度,而簇间的相似度较低。首先随机选择K个对象,每个对象初始地代表了一个簇的平均值或中心。对剩余的每个对象根据其与各个簇中心的距离,将它赋给最近的簇。然后重新计算每个簇的平均值。不断重复该过程,直到准则函数收敛。
1.1.2 K-means算法具体步骤
问题提出:给定一个元素集合D,其中每个元素具有n个可观察属性,将D划分为k个子集,要求每个子集内部的元素之间相异度尽可能低,而不同子集的元素相异度尽可能高。
算法步骤如下:
1.从D中随机取k个元素,作为k个簇的各自的中心
2.分别计算剩下的元素到k个簇中心的相异度,将这些元素分别划归到相异度最低的簇
3.依据聚类结果,重新计算k个簇各自的中心,计算方法是取簇中所有元素各自维度的算数平均值。
4.将D中全部元素按照新的中心重新聚类。
5.重复第4步,直到聚类结果不再变化。
6.将结果输出。
1.1.3 K-means算法存在的问题
原始的K-means算法选取K个点作为初始聚类中心,然后进行迭代操作,其中存在以下的几个问题。
1.K值的确定。
K-means算法首先选择K个初始质心,其中K是用户指定的参数,即所期望的簇的个数,这么做的前提是已知数据集中包含簇的个数,但是在很多情况下,我们并不知道数据的分布情况,实际上聚类就是我们发现数据分布的一种手段,所以,K值的确定对K-means聚合结果至关重要。
2.初始质心的选取
选择适当的初始质心是基本K-means算法的关键。常用的方法是随机选取初始质心,但是,这样簇的质量常常很差。
3.距离的度量
常用的距离度量方法包括:欧几里得距离和余弦相似度。两者都是评定个体间差异的大小的。欧几里得距离度量会受指标不同单位刻度的影响,所以一般需要先进性标准化,同时距离越大,个体间差异越大;空间向量余弦夹角的相似度度量不会受指标刻度的影响,余弦值落于[-l,1],值越大,差异越小。
1.1.4 现有的改进的K-means算法
针对以上问题,现在有很多改进的K-means算法,例如基于聚类数和初始值的K-means算法改进研究,提出了一种基于密度选取初始质心和采取遗传算法优化聚类数k的算法。该算法在一定程度上解决了初始质心和聚类数k对聚类精度和效率的影响,提高了聚类的准确率。
2 改进的K-means算法
2.1 改进算法概述
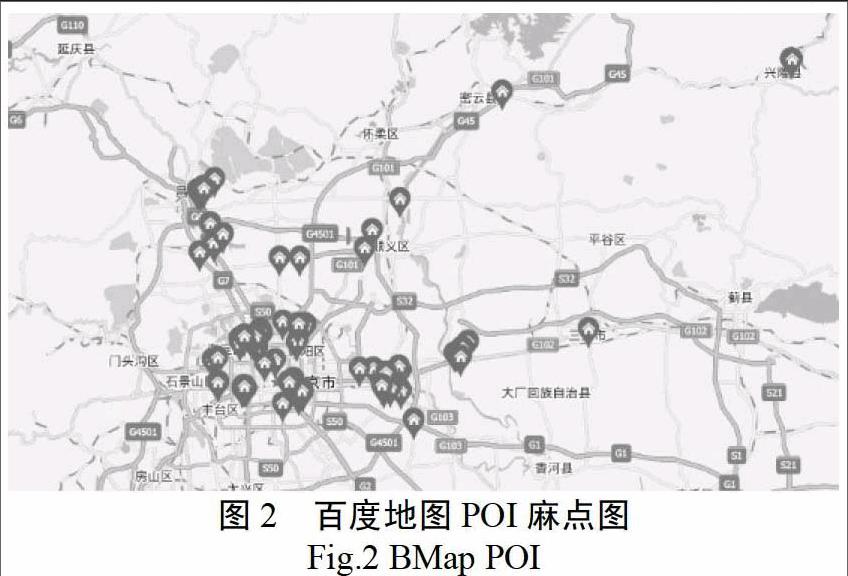
地图定位或导航都会指向某种生活服务,这些服务通过POI数据来展现。POI包含名称、类别、经纬度等信息。例如,现在百度上能够找到3800万个POI数据,这些数据中,有2000万个与生活服务深度关联,当然,不止百度,高德等都从未停止对POI的采集与应用。百度地图上的POI数据越来越多,如果直接全部展示到地图上,便会出现POI点图标过密,尤其当地图缩放到一定级别时,甚至出现信息覆盖等现象,如下图2所示,这样使得地图可用性大大降低,为更友好地展示POI信息点,需要对这些POI进行聚合。
本文在百度地图的基础上对k-means算法进行改进,利用现有的百度地图的坐标体系,可以实现确定k的初始值和k个初始簇质心的计算。
2.2 百度地图API简介以及坐标体系概述
百度地图API是一套有Javascript编写的将百度地图嵌入到网页应用程序接口,它能够帮助您在网站中构建功能丰富、交互性强的地图应用程序。百度地图API为开发者提供丰富的函数、空间、事件和封装的类,提供很多的专题服务,如本地搜索、路线规划、地址解析等接口工用户使用。开发者只需要按照百度的要求进行注册使用,通过API,利用Javascript脚本语言就可以将百度地图服务连接到自己的网页中陆1。
在百度API中,有如下坐标系:
1.经纬度
通过经度(longitude)和纬度(latitude)描述地球上的某一个位置
2.平面坐标
投影之后的坐标(用x和y描述),用于在平面上标识某个位置,百度地图API默认使用墨卡托投影(Mercator Projection),平面坐标是以最大级别18级为基准的。即在18级下,平面坐标的一个单位就代表了屏幕上的一个像素。平面坐标与地图所展示的级别没有关系,也就是说在1级和18级下,天安门位置的平面坐标都是一致的。某个位置的平面坐标可以通过BMap.MercatorProj ection类来完成,该类提供经纬度与平面坐标互相转换的方法。例如天安门的经纬度大约是116.404,39.915,经过转换即可得到平面坐标:
var projection=new BMap.MercatorProjection();
var point=projection.lngLatToPoint (newBMap.Point (116.404, 39.915》;
得到结果就是12958175,4825923.77就是平面坐标。可以理解为18级下,天安门距离坐标原点的位置差为12958175,4825923.77,单位为像素。
3.像素坐标
描述不同级别下地图上某点的位置,在第18级别下,我们直接将平面坐标向下取整就得到了像素坐标,而在其他级别下可以通过如下公式进行换算:
像素坐标=|平面坐标x2 zoom-18|
比如经过计算,在第4级天安门位置的像素坐标是:790,294.
4.图快坐标:
地图图块编号,百度地图API在展示地图时是将征地地图切割成若干图块显示的,当地图初始化或是地图级别、中心点位置发生变化时,地图API会根据当前像素坐标计算出视野内需要的图块坐标(也叫图块编号),从而加载对应的图块用以显示地图。百度地图的图块坐标原点与平面坐标一致,从原点向右上方开始编号为0,0。
某个位置的图块坐标可以通过如下公式计算:
图块坐标=l像素坐标÷2561
256实际上是每个图块的宽度和高度,我们用像素坐标除以这个数就知道图块坐标了。还以天安门为例,在第4级下天安门所在的图块编号为:3,1,而在第18级下,图块编号为:50617,18851
5.可视区域坐标
地图可视区域的坐标系(用x和y描述),地图都是显示在确定大小的矩形框中的,这个矩形框通常是开发者在初始化地图传入的某个容器元素。这个矩形框也有自己的坐标系,在百度地图API中称之为可视区域坐标系,它的原点位于矩形的左上角。通过Map类的pointToPixel和pixeIToPoint方法可以相互转换经纬度坐标与可视区域坐标。
6.覆盖物坐标
覆盖物相对于容器的坐标(用x和y描述),覆盖物在实现上就是若干DOM元素,这些元素会被放在若干覆盖物容器内(具体请参考地图API开发指南),那么覆盖物的坐标实际上就是相对于这些覆盖物容器的坐标。
2.3 基于网格的改进的K-means算法
原始的K-means算法选取K个点作为初始聚类中心点,然后进行迭代操作,初始点选取不同可能获得不同的聚类结果。本文主要提出用改进的Kmeans算法来解决百度地图上POI聚合的问题。改进主要是利用百度地图的坐标体系,以及针对传统的K-means算法中存在的问题,提出初始K值的选择以及K个初始质心的选择方法。
2.3.1 改进的K-means算法思想
针对上文提到的传统K-means算法存在的问题,K-means的初始K值的确定以及K个初始质心的选择会明显的影响聚合结果。本文提出一种新的基于网格的K-means算法,其创新之处在于网格的确定、k值的选择、k个初始质心的选择。
1.基于网格以及K值的选择
百度地图可以看作是将整个地图图片切割成若干个图块显示的,每一个图块就可以看作一个网格。在百度地图每个缩放级别下,每个POI都有其唯一对应的图块坐标。基于网格的思想是指每个POI有对应的网格,网格的个数就是K值。在此,每个POI的图块坐标计算过程如下:
(a)可以依据百度地图提供的API计算出其平面坐标:
var projection= new BMap.MercatorProjection();
var point = projection.lngLatToPoint (newBMap.Point (116.404. 39.915》;
(b)依据平面坐标可以根据公式计算出其像素坐标:
像素坐标=|平面坐标x2zoom-18|
(c)依据像素坐标,即可得到POI对应的图块坐标:
图块坐标=|像素坐标÷256|
2.K个初始质心的选择
在百度地图某个缩放级别下,所有POI的个数是n,即原始数据集合(xl,x2,…,xn),此处的每个XI为二维向量,所有POI所在的图块为k个,即将原始数据分成k类S={S1,S2,…,Sk}。在此,每个初始质心指对应图块中所有的POI点的各维度的算数平均数,则初始质心坐标为:
其中m为每个质心的POI个数。
2.3.2 改进的K-means算法描述
百度地图为用户提供地图位置搜索、展示、POI检索等多种服务,而上文提到的丰富的坐标体系是这些服务的基础。在本文中,把百度地图丰富的坐标体系元素融入到现有的基于网格的K-means算法中。充分利用百度地图的图块坐标和像素坐标等,巧妙地实现网格的划分,以及K-means中k值的选择与质心的确定。这样,即使POI点的数量增加,也不会出现覆盖现象。
百度地图POI聚合中,基于网格的改进的K-means算法描述如下:
输入:百度地图上的POI,即n个坐标点。
输出:在百度地图的不同缩放级别下,实现n个POI点的聚合为k个聚类中心。
Begin
取样,获取n个坐标点(即POI点的坐标),在百度地图的某一个缩放级别下,计算出n个坐标点的图块坐标,分别为(X1,Yl)、(X2,Y2)….(Xn,Yn),得到k个不同的图块坐标即分为k个聚类{SI,S2,…,Sk};
计算出每个簇中POI点的个数为m;设k个质心的像素坐标为(XI,Y1)、(X2,Y2)…(Xk,Yk)
Forl=1 to k do
为每个聚类中的POI点的个数
//计算出k个聚类的初始质心;
Repeat
分别计算剩下的元素到k个簇中心的相异度,将这些元素分别划归到相异度最低的簇。在此处是利用像素坐标间的距离计算出各个POI点的坐标到k个质心间的距离,将POI点归到距离它最近的那个质心。即:
//minDic初始化为Double.MAX_VALUE,每个POI点像素坐标坐标为(xh,yh),每个质心像素坐标
//计算每个POI点到质心的距离找到离得最近的质心点
If
dic minDic=dic End End 根据聚类结果,重新计算k个簇各自的中心,计算方法是取簇中所有元素各自维度的算术平均数。 Until设定迭代终止条件mu(如IE-IO),当各个新质心相对于老质心偏移量小于mu时,终止迭代。 End 如下图3中,百度地图有POI若干,在地图缩放级别为15时,它们的像素坐标如表一中第三列所示,按照文本提出的算法进行聚合,首先这写POI点分属于四个图快坐标,分别为(6325.0,2359.0)、(6325.0, 2360.0)、(6326.0, 2361.0)和(6331.0,2363.0),所以k值初始化为4,即将这些POI点聚合于四簇,利用算法进行聚合之后的四个簇的中心点,如表1所示。 按照本文改进的算法计算出的聚合结果为下表1所示,其中POI点的坐标是百度坐标体系中的像素坐标。 3 结论 本文给出了基于网格的改进的K-means算法。该算法提出背景在于提出适用于应用在地图上的聚合算法。利用百度地图的坐标体系,实现不同缩放级别下POI的聚合,是本文的直接目标。改进的算法吸取了传统Kmeans算法的优点,充分利用并结合地图的特点,巧妙地实现了地图上的POI的聚合。
