围压下裂隙对地震波速度影响的物理实验研究

赵卫华，王红才，魏建新，孙东生，李阿伟

(1.中国地质科学院地质力学研究所，北京 100081；2.国土资源部新构造与地质灾害重点实验室，北京 100081；3.中国石油大学(北京)CNPC重点实验室，北京 102249)

围压下裂隙对地震波速度影响的物理实验研究

赵卫华1,2，王红才1,2，魏建新3，孙东生1,2，李阿伟1,2

(1.中国地质科学院地质力学研究所，北京 100081；2.国土资源部新构造与地质灾害重点实验室，北京 100081；3.中国石油大学(北京)CNPC重点实验室，北京 102249)

构建了等直径不同裂隙密度和等裂隙密度不同裂隙直径两组物理模型，进行不同围压条件下多方向的超声波速度测试，并运用Hudson理论进行了理论模型计算。结果显示，计算与实测结果吻合较好。随围压的增大，纵、横波速度均近线性增加，纵、横波各向异性基本保持不变；裂隙密度从2%增大到6%，纵波速度不同程度降低，其中慢纵波降低幅度相对较大，快横波变化不明显，而慢横波则大幅降低。随着裂隙密度的增大，纵、横波各向异性均增大，且横波各向异性增加速率大于纵波；裂隙直径从2 mm增大到3 mm，快纵波速度增加很小，慢纵波增加明显，横波速度均不发生改变。随着裂隙直径的增大，纵波各向异性逐渐降低，横波各向异性保持不变。最后结合试验结果分析了Hudson理论在不同深度进行参数预测的必要条件。研究结果有助于油气生产、地下水的开采与控制、污染处理等。

裂隙；Hudson理论；物理模型；波速；围压

地壳岩体中普遍发育裂隙和断层，这些裂隙和断层是影响岩层结构力学性质和连通性的重要因素，受地应力的作用，这些裂隙通常在空间上相互平行分布[1～5]。裂隙可以是储集空间，也可以是渗流通道，在油气成藏理论分析与开发设计中都受到了密切的关注[4～5]。利用实验室制作的人工物理模型进行弹性波速测试，是研究裂隙对地震波性质影响的一个重要手段[6～11]。Hudson理论能够定量分析裂隙的密度、高宽比等对裂隙介质弹性参数的影响[12～16]。地下岩石裂隙系统处于一定的地应力环境之中，应力变化会影响基质和裂隙材料的弹性性质[17～22]，围压下人工模型裂隙对地震波速度的实验测试能够研究Hudson裂缝介质理论在不同深度条件下的应用，并对理论和相关数据的拓展应用提供实验支持，因此具有重要的理论与现实意义。

1 模型制作

基于Hudson理论，用等重量的环氧树脂多次分层浇铸作为基质，在环氧树脂层间置入等厚的硬币状橡胶模拟裂隙，每层均匀置入等量等厚的裂隙材料[6～7,11]。模型的裂隙密度由ε=Nr3/V公式计算得出，其中N是裂隙的总个数，r是裂隙圆片的半径，V是模型体积[14]。首先制作出均匀的立方体，再钻取3个直径25 mm相互正交的圆柱状试样(X、Y、Z)进行实验，其中X、Y相互垂直平行于裂隙材料定向分布形成的面理，Z样品垂直于面理，圆柱两端经过磨床抛光，平整度达到0.5%。样品裂隙分布如图1所示。

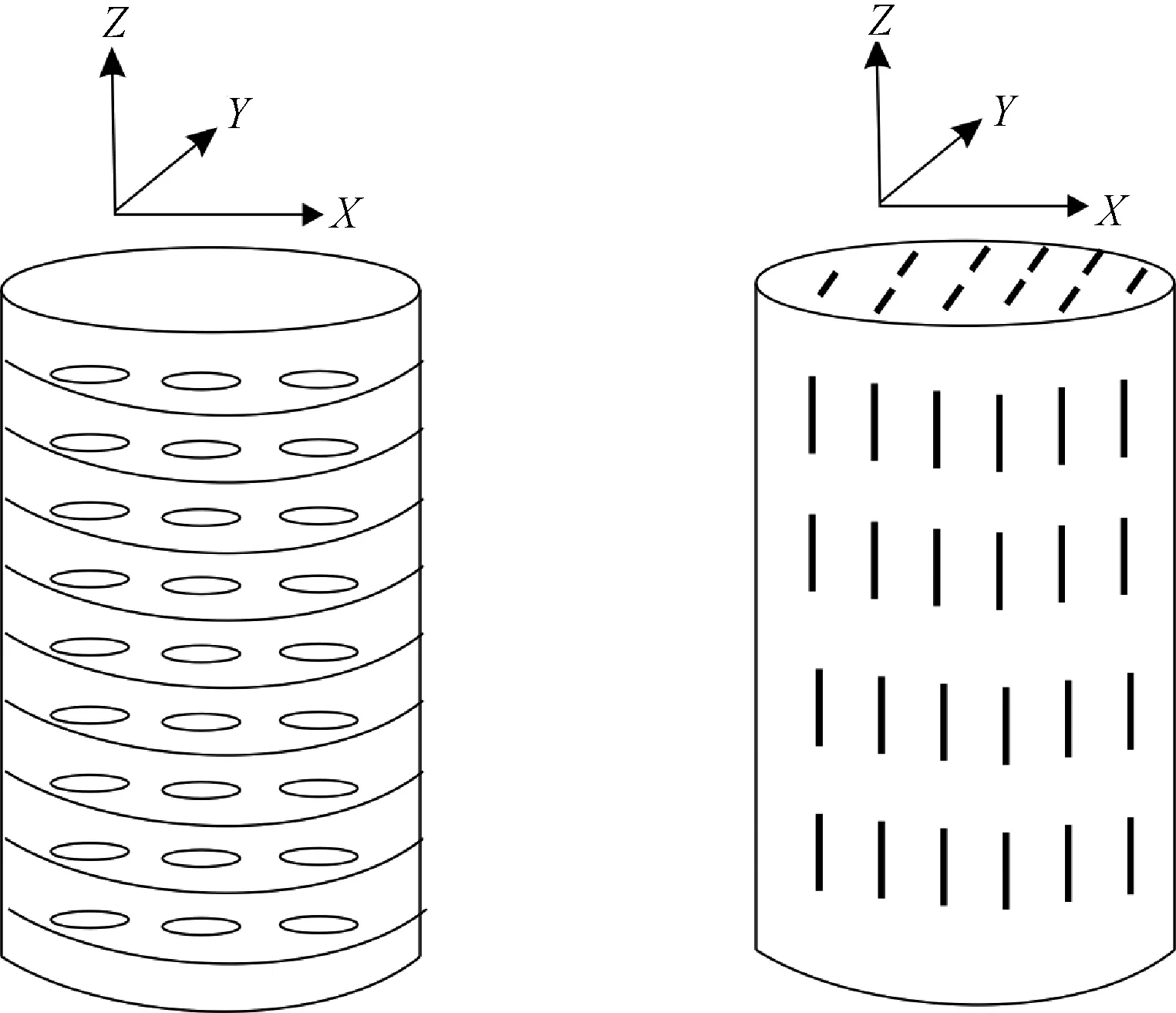
图1 样品裂隙分布与XYZ分布示意图Fig.1 Simplified diagram of distribution of crack and X Y Z

考虑裂隙密度和裂隙高宽比2个影响因素，制作了两组样品：第一组，相同裂隙直径2 mm，裂隙密度分别是2%、4%、6%的模型3块；第二组，相同裂隙密度4%，裂隙直径分别为2 mm、2.5 mm和3 mm的模型3块。采用分层浇铸制作了纯基质(裂隙密度为0)样品1块(编号M1)；此外还将裂隙材料做成块状，钻取柱状样品(编号M0)。分组编号及单个柱体物理参数见表1。

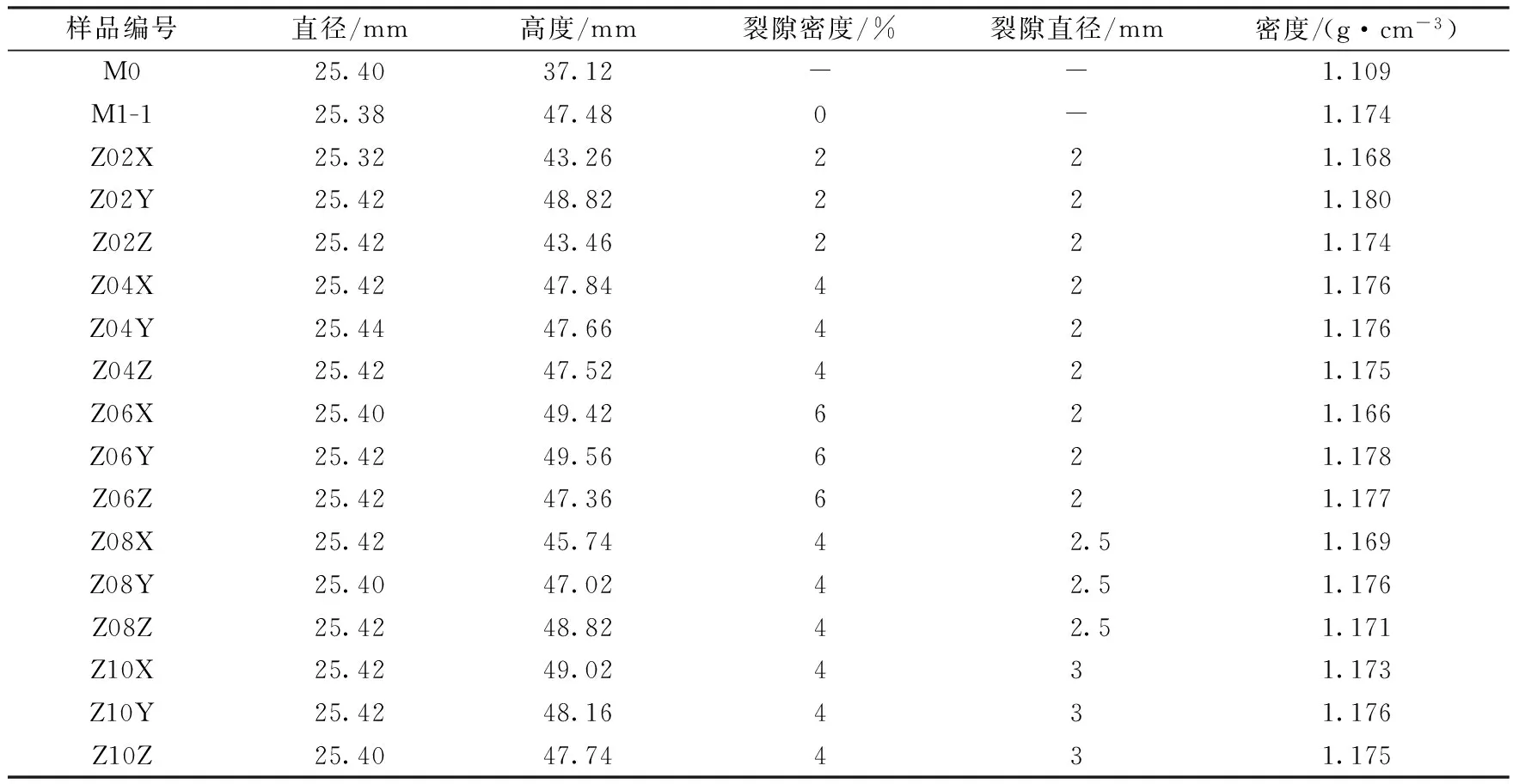
表1 样品参数信息

2 试验测试

应用美国NER公司生产的AutoLab2000C岩石物性测试系统进行了波速测量，脉冲透射法三分量探头一次触发能够获取纵波和相互垂直的两个横波等3个信号，其中纵波换能器频率700 kHz，横波换能器频率500 kHz，测试误差小于0.5%。试验获得了样品在0～25 MPa围压条件下的纵、横波速度。对于裂隙材料，由于其柔软的特性，仅进行了常压条件下的速度测量，纵波速度为1385 m/s，未测到横波信号；对于分层浇铸无裂隙样品M1-1(纯基质)，无围压条件波速测试结果表明3个方向的纵波速度和6个横波速度分量各自近似相等，因此可认为基质为均匀各向同性。纵波速度测试结果用VpXX(快纵波)、VpYY(中间纵波)和VpZZ(慢纵波)表示，分别代表X、Y、Z方向的纵波速度。横波速度用Vs后加两个字母表示，第一个字母表示传播方向，第二个字母表示偏振方向，例如VsXZ表示传播方向为X偏振方向为Z的横波速度。波速由公式V=1/t计算得出，其中t为首波到时。

3 试验结果

试验结果表明，随着围压的增大，样品的纵、横波速度都近线性增加。纵波速度VpXX与VpYY近似相等且大于VpZZ；横波速度VsXY与VsYX近似相等，VsXZ、VsZX、VsYZ与VsZY近似相等且小于VsXY与VsYX，这符合横向各向同性样品的特征。图2显示了样品Z04纵波、横波速度随围压的变化。

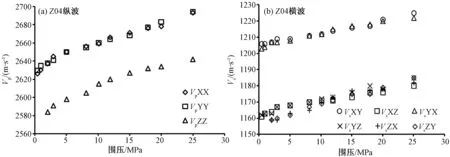
图2 样品Z04 实测纵、横波速度随围压的变化Fig.2 The measured Vp and Vs varying with the confining pressure (Sample Z04)

4 理论计算及结果对比

根据Hudson理论，应用基质和裂隙材料的剪切模量、拉梅系数和宽高比等参数，经修正计算可得到理论上的裂纹模型的纵横波速度[12～13]。本文应用分层浇铸基质样品升压至25 MPa的不同围压条件下实测波速计算得出的弹性参数、裂隙介质的弹性常数，结合给定裂隙尺寸及裂隙密度，计算了不同围压下含裂隙集合体的快慢纵横波速度。计算结果与实测结果随围压变化有近似的变化规律，高围压时计算与实测结果吻合很好，低围压下个别数据误差相对较大主要是探头与样品端面耦合不好造成的，实测数据与计算数据之差在±0.5%之内。图3显示了样品Z02实测纵、横波速度与理论计算结果随围压的变化。

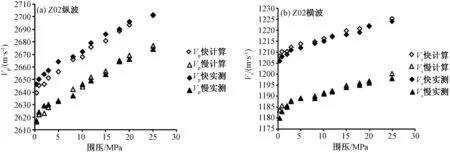
图3 样品Z02实测与计算纵、横波速度随围压的变化Fig.3 The measured and calculated Vp and Vs varying with the confining pressure (Sample Z02)

5 分析与讨论

5.1 裂隙密度变化对模型弹性性质及各向异性的影响

基于Hudson理论实测并计算了裂隙直径2 mm，裂隙密度分别为2%、4%和6%的3个模型的波速及各向异性，分析裂隙密度的变化对横向各向同性介质弹性性质的影响。图4a显示了3种裂隙密度样品快、慢纵波速度随围压的变化，随着围压的增大，3种裂隙密度的样品纵波速度均近似保持同样的速率线性增加。裂隙密度在2%～6%之间，随着裂隙密度的增大快纵波与慢纵波速度不同程度地降低，慢纵波降低幅度较大，这与前人常压条件下的试验结果[6]变化规律一致。图4b给出了3种裂隙密度样品横波随围压的变化，图中显示，裂隙密度在2%～6%之间，随着裂隙密度增大，快横波速度变化不明显，慢横波速度则大幅降低。

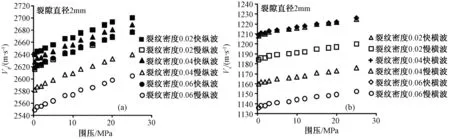
图4 直径2 mm的3种裂隙密度模型纵、横波速度随围压的变化Fig.4 Vp and Vs of 3 samples (crack diameter 2 mm) with different crack density varying with confining pressure

各向异性是进行波速分析从而描述岩石波速性质的重要指标，本文应用Thomson提出的弱弹性各向异性的表示方法[23～25]进行了各向异性分析，以ζ和γ分别代表波速的纵波和横波的各向异性，定义如下：

式中：C11、C33、C66和C44为弹性模量，根据基质和裂隙材料的剪切模量、拉梅系数计算获得[12～13]。图5a显示了裂隙直径2 mm的3种不同裂隙密度样品纵波各向异性随围压的变化，随围压增加，纵波各向异性几乎不发生变化，这也说明引起各向异性的裂隙本身的弹性性质没有发生改变；其次，裂隙密度从2%增大到6%，纵波各向异性显著增加。图5b显示了裂隙直径2 mm的3种不同裂隙密度样品横波各向异性随围压的变化，横波各向异性与纵波各向异性的变化规律一致，在数值上，横波各向异性远大于纵波各向异性。

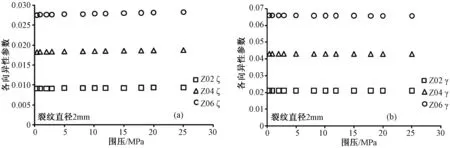
图5 直径2 mm的3种裂隙密度模型纵、横波各向异性随围压的变化Fig.5 Vp and Vs anisotropy of 3 samples (crack diameter 2 mm) with different crack density varying with confining pressure

图6显示了25 MPa围压条件下，裂隙直径2 mm的3种裂隙密度样品纵、横波速度各向异性与裂隙密度的关系，回归分析得出，纵、横波速度各向异性与裂隙密度线性相关，裂隙密度在2%～6%之间，随着裂隙密度增大，各向异性线性增大，且横波各向异性增加的速率要远大于纵波各向异性增加的速率，这也说明在此裂隙密度范围内，横波各向异性对于裂隙密度的改变更加敏感。此外，通过纵、横波各向异性与裂纹密度的拟合公式，计算得出在裂纹密度为0即无裂纹时各向异性近似为0，这与实际情况相符，可以作为试验数据向0裂纹密度线性推断的依据。

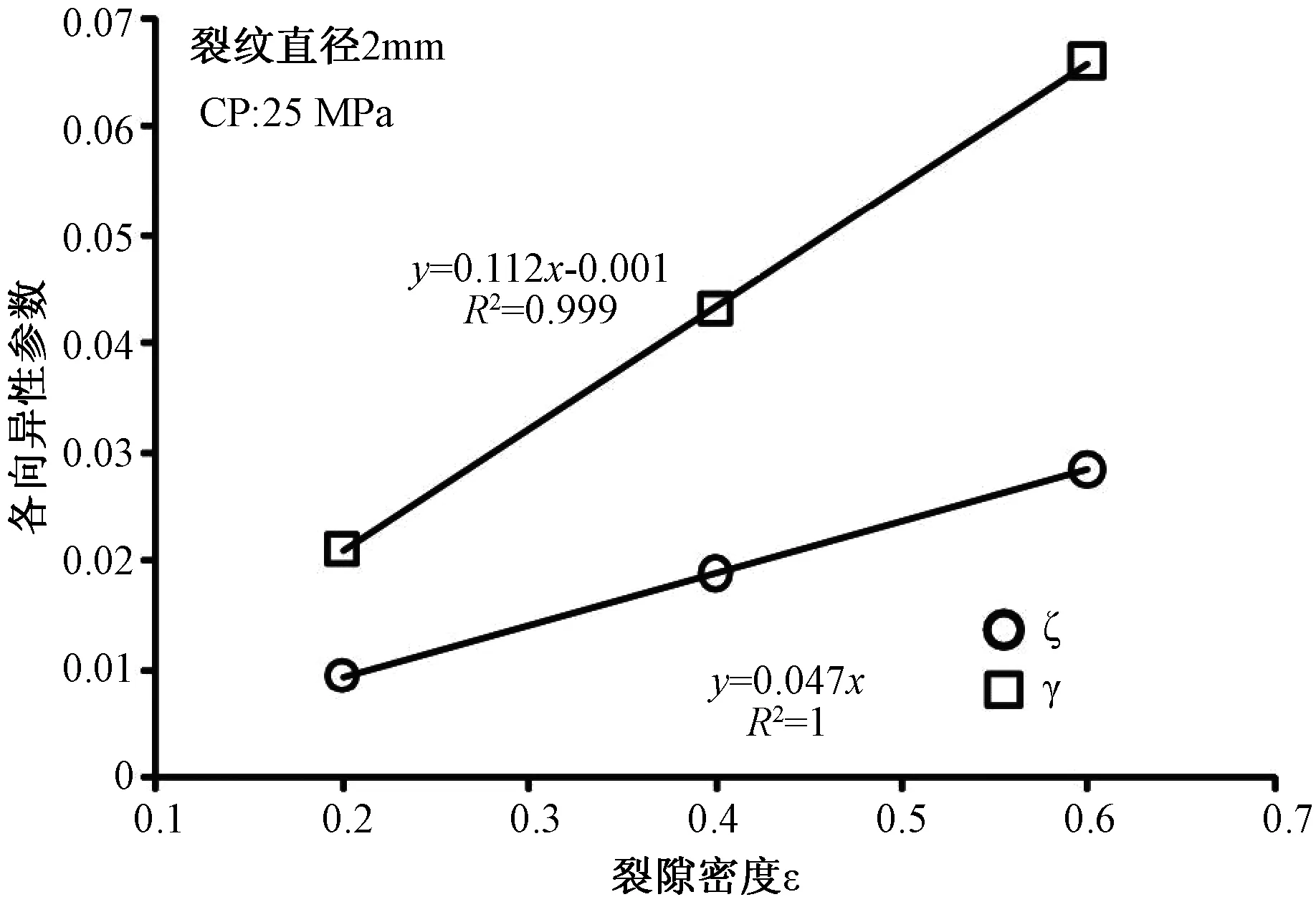
图6 围压25 MPa直径2 mm的3种模型纵、横波各向异性随裂隙密度的变化Fig.6 Anisotropy of 3 samples varying with crack density (crack diameter 2 mm, confining pressure 25 MPa)

5.2 裂隙直径变化对模型弹性性质及各向异性的影响

应用Hudson理论，本文实测并计算了裂隙密度4%，裂隙直径分别是2.0 mm、2.5 mm和3.0 mm的3个模型的纵、横波速度，研究裂隙直径变化对横向各向同性介质弹性性质的影响。模型制作采用等厚度的裂纹，因此裂纹直径的改变反映了裂纹宽高比的变化，进行分析时，选取裂隙直径作为变量。

如图7a，随着围压的增大，3种直径的样品纵波速度均近似以同样的速率线性增加。裂隙直径从2 mm增大到3 mm，快纵波速度稍有增加，慢纵波速度增加明显。图7b显示了3种裂隙直径的样品横波速度随围压的变化，从中可见裂隙密度4%，裂隙直径从2 mm增加到3 mm，快、慢横波速度均不变。

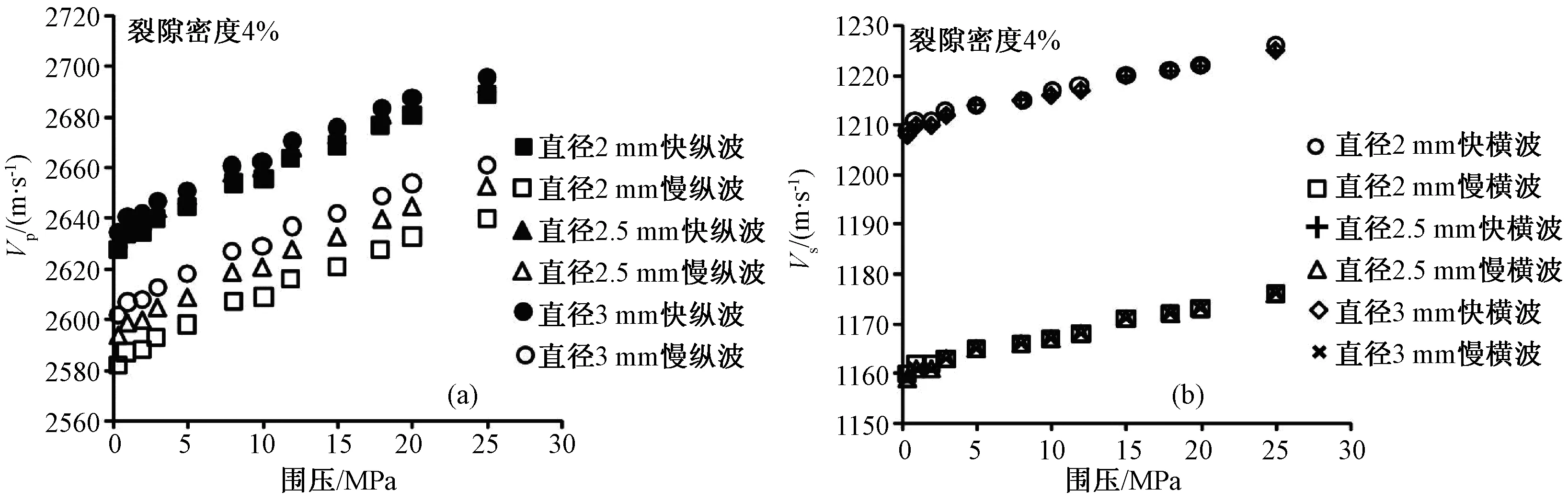
图7 裂隙密度4%的3种直径模型纵、横波速度随围压的变化Fig.7 Vp and Vs of 3 samples with different diameter varying with confining pressure(crack density 4%)

图8a显示了3种等裂隙密度样品纵波各向异性随围压的变化，随围压增大纵波各向异性基本保持不变，随裂隙直径增大，纵波各向异性降低；图8b给出了3种样品横波各向异性随围压的变化，横波各向异性随围压与直径改变均不变。

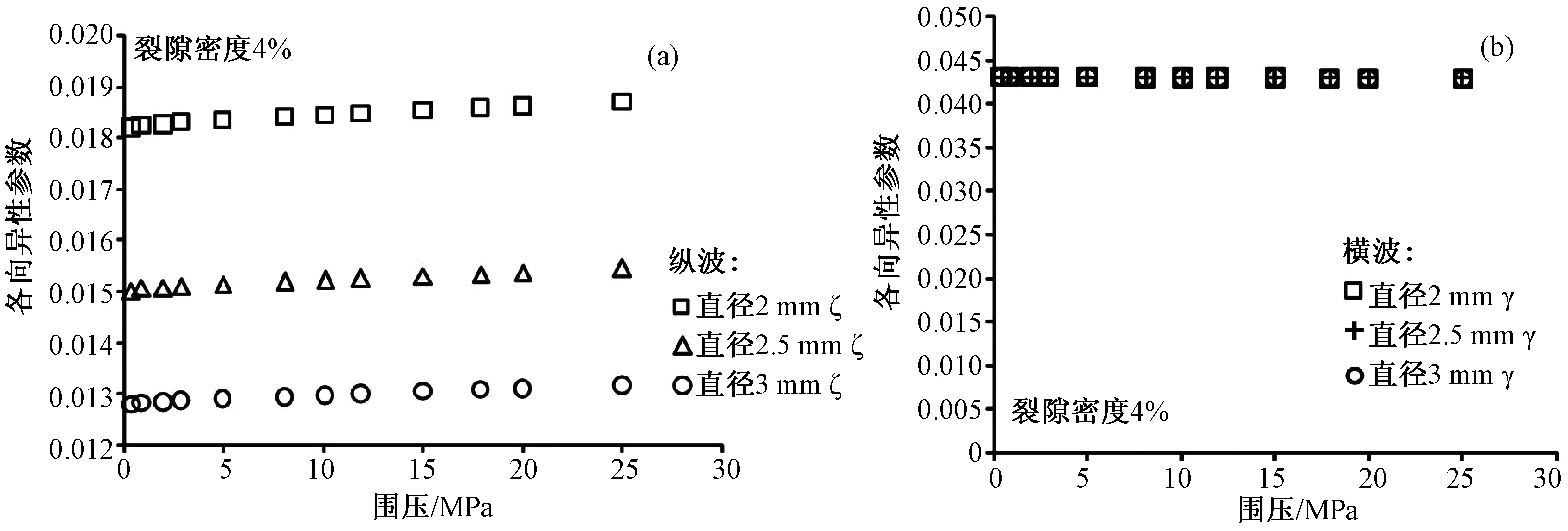
图8 裂隙密度4%的3种直径模型纵、横波各向异性随围压的变化Fig.8 Vp and Vs anisotropy of 3 samples with different crack diameters varying with confining pressure (Crack density 4%)

图9显示了25 MPa围压条件下，4%裂纹密度的3种裂隙直径样品纵、横波各向异性随裂隙直径的变化，可见在数值上横波各向异性远大于纵波各向异性，随裂隙直径增加，横波各向异性保持不变，纵波各向异性逐渐降低。

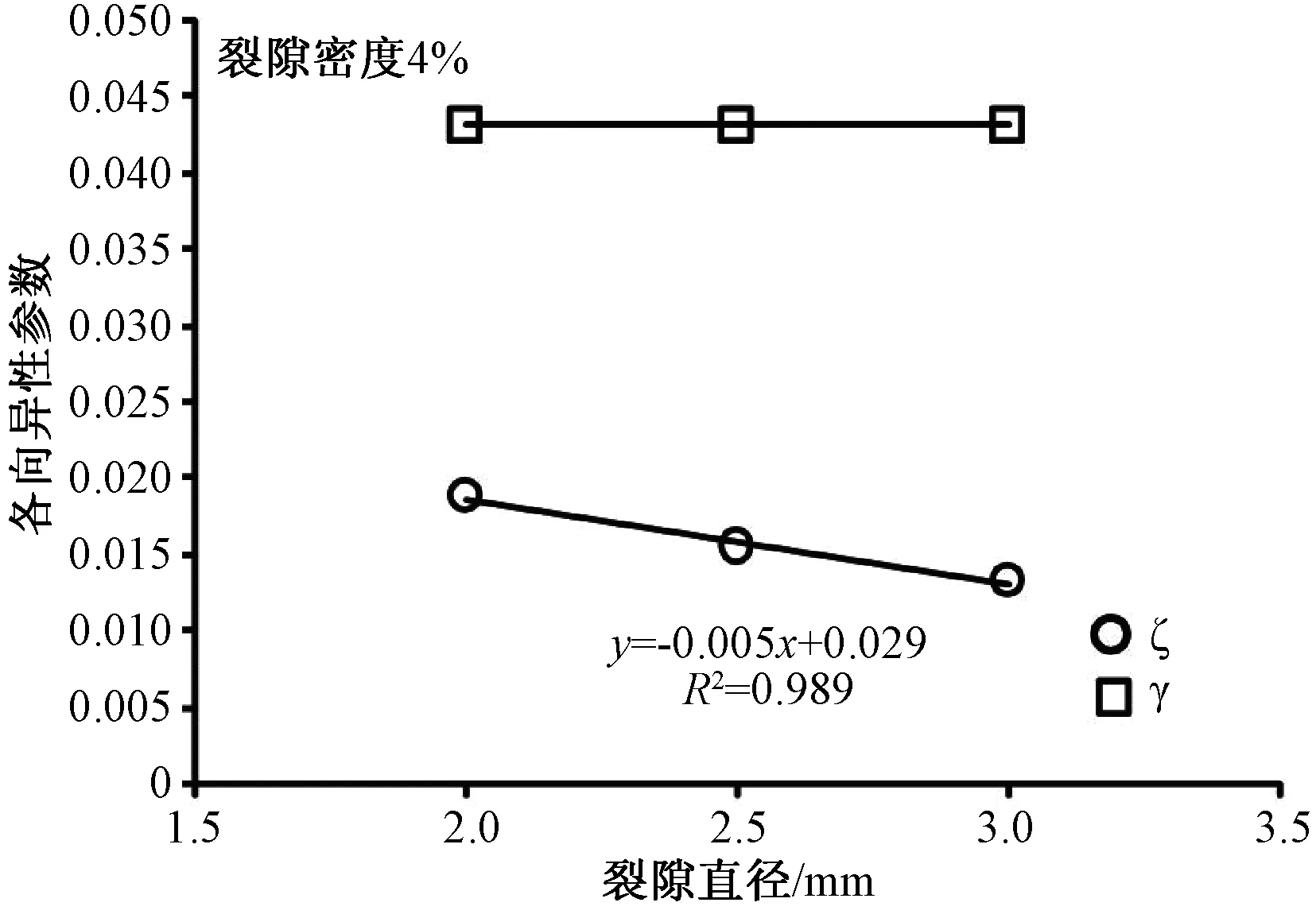
图9 围压25 MPa裂隙密度4%的3种模型纵、横波各向异性随裂隙直径的变化Fig.9 Anisotropy of 3 samples varying with crack diameters (Crack density 4%, confining pressure 25MPa)

5.3 Hudson理论在不同深度条件下应用的初步讨论

基于Hudson理论，制作横向各向同性物理模型，实测并计算了相同直径3种不同裂隙密度与相同裂隙密度3种不同裂隙直径的6个样品0～25 MPa围压条件下的纵(3个分量)、横波(6个分量)速度。对比发现，实测结果与理论计算的结果吻合较好，证明物理模型是有效的，能够运用Hudson理论进行深部地震波性质以及裂隙参数分析。

基质材料的近似各向同性与基质材料本身弹性性质不发生改变是Hudson理论的基础条件，随围压的改变材料只发生弹性变形，裂隙本身与材料颗粒的接触关系不发生改变。0～25 MPa围压条件下的地震波速度计算时，运用了基质材料0～25 MPa围压条件下的实测弹性参数，取得了很好的结果。

实际岩石应用条件非常复杂，基质颗粒的边界接触条件是一个重要的影响因素，对于低孔低渗的结晶岩，需要考虑矿物颗粒之间的接触关系；但是对于相对高孔隙度的砂岩，围压改变会轻易地改变颗粒的接触条件以及理论裂隙的高宽比，这使得理论的应用变得更加复杂。除了要考虑颗粒间的接触关系之外，还要考虑基质空隙的变化，在这方面，需要进行更加深入的探讨。

6 结论

应用Hudson理论制作了不同裂隙密度与裂隙直径的横向各向同性人工样品，运用基质样品在0～25 MPa围压条件下的实测弹性常数计算了理论模型的纵、横波速度，计算结果与实测结果吻合较好。

随围压的增大，模型纵、横波速度均近线性增加。裂隙密度从2%增大到6%，纵波速度不同程度地降低，慢纵波降低幅度相对较大，快横波几乎不发生改变，慢横波大幅降低。在裂隙密度2%～6%的范围内，纵、横波各向异性与裂隙密度线性相关，横波各向异性远大于纵波各向异性；随着裂隙密度的增大，纵、横波各向异性逐渐增大，并且横波各向异性增加的速率要远大于纵波各向异性增加速率。

裂隙直径从2 mm增大到3 mm，快纵波增加很小，慢纵波增加相对明显，快、慢横波速度均不发生改变。随着围压的增大，纵、横波各向异性基本保持不变。裂隙密度4%，直径从2 mm增大到3 mm，纵波各向异性逐渐降低，横波各向异性保持不变。

实际分析裂隙的情况时，除了要考虑围压对基质弹性性质的影响外，还需要关注岩石本身的颗粒边界条件和孔隙等性质。

[1] Crampin S, Evans R, Üçer B, et al. Observations of dilatancy-induced polarization anomalies and earthquake prediction[J]. Nature, 1980, 286: 874～877.

[2] Crampin S. A review of wave motion in anisotropic and cracked elastic-media[J]. Wave Motion, 1981, (3): 343～391.

[3] Crampin S, Sheila P. A review of shear-wave splitting in the compliant crack-critical anisotropic Earth[J]. Wave Motion, 2005, 41∶ 59～77.

[4] 刘恩儒,曾新吾. 裂缝介质的有效弹性常数[J]．石油地球物理勘探, 2001, 36(1): 37～44.

LIU En-ru, ZENG Xin-wu. Effective elastic constant of fractured medium[J]. Oil Geophysical Prospecting, 2001, 36(1): 37～44.

[5] 韩开锋, 曾新吾. Hudson理论中裂隙参数的适用性研究[J]. 石油物探, 2006, 45(5):435～440.

HAN Kai-feng, ZENG Xin-wu. Study of the boundary element method on applicability of fracture parameters in Hudson theory[J]. Geophysical Prospecting for Petroleum, 2006, 45(5): 435～440.

[6] 魏建新,狄帮让.裂隙密度对纵波传播特性影响的实验观测[J].石油地球物理勘探,2007,42(5):554～559.

WEI Jian-xin, DI Bang-rang. Experimentally surveying influence of fractural density on P-wave propagating characters[J]. Oil Geophysical Prospecting, 2007,42(5): 554～559.

[7] 魏建新,狄帮让. 裂隙张开度对地震波特性影响的模型研究[J]. 中国科学(D辑)，2008,(增刊Ⅰ):211～218.

WEI Jian-xin, DI Bang-rang. Study on the impact of seismic wave characteristics of crack aspect ratio[J]. Science in China (Series D), 2008, (Supp. I): 211～218.

[8] 齐宇，魏建新，狄帮让，等. 横向各向同性介质纵波方位各向异性物理模型研究[J]. 石油地球物理勘探, 2009, 44(6): 671～674, 689.

QI Yu, WEI Jian-xin, DI Bang-rang, et al. Compressional wave (P-wave) azimuthal anisotropyphysical model studies in transversally isotropic me-dium[J]. Oil Geophysical Prospecting,2009,44(6):671～674,689.

[9] 魏建新, 狄帮让.岩石柱塞样品超声横波速度测试精度分析[J].石油地球物理勘探, 2012,47(6): 918～925.

WEI Jian-xin, DI Bang-rang. Test accuracy analysis of S-wave velocity on rock core sample[J]. Oil Geophysical Prospecting, 2012, 47(6): 918～925.

[10] 魏建新，狄帮让.周期层状介质对纵波速度影响的实验研究[J].石油地球物理勘探, 2010,45(5):661～666.

WEI Jian-xin, DI Bang-rang. Experimental research on P-wave velocity of periodic layered media[J]. Oil Geophysical Prospecting, 2010, 45(5): 661～666.

[11] 尹志恒, 狄帮让, 魏建新, 等.裂缝参数对纵波能量衰减影响的物理模型研究[J].石油地球物理勘探, 2012,47(5):728～734,753.

YIN Zhi-heng, DI Bang-rang, WEI Jian-xin, et al. P-wave attenuation by fracture parameter in physical models[J]. Oil Geophysical Prospecting, 2012, 47(5): 728～734, 753.

[12] Hudson J A. Overall properties of a cracked solid[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1980, 88: 371～384.

[13] Hudson J A. Wave speeds and attenuation of elastic waves in material containing cracks[J]. Geophysical Journal International, 1981, 64(1): 133～150.

[14] Hudson J A. A higher order approximation to the wave propagation constants forcracked solid[J]. Geophysical Journal International, 1986, 87(1): 265～274.

[15] Hudson J A, Liu E, Crampin S. The mechanical properties of materials with interconnected cracks and pores[J]. Geophysical Journal International, 1996, 124(1)：105～112.

[16] Hudson J A, Pointer T, Liu E. Effective medium theories for fluid saturated materials with aligned cracks[J]. Geophysical Prospecting, 2001，49(5): 509～522.

[17] Hess H. Seismic anisotropy of the uppermost mantle under oceans[J]. Nature, 1964, 203: 629～631.

[18] Ji S C, Saruwatari K, Mainprice D, et al. Microstructures, petrofabrics and seismic properties of ultrahigh-pressure eclogites from Sulu region, China: Implications for rheology of subducted continental crust and origin of mantle reflections[J]. Tectonophysics, 2003, 370: 49～76.

[19] 杨顶辉，张中杰，滕吉文，等. 双相各向异性研究、问题与应用前景[J]. 地球物理学进展，2000，15：7～21.

YANG Ding-hui, ZHANG Zhong-jie, TENG Ji-wen, et al. The study of two-phase anisotropy questions and applied prospects[J]. Progress in Geophysics, 2000, 15: 7～21.

[20] 张中杰，滕吉文，陈运泰. 地球物理学的回顾与展望[J]. 地球物理学进展，2001, (5)：345～352.

ZHANG Zhong-jie, TENG Ji-wen, CHEN Yun-tai. Geophysics: The 20thCentury in retrospect and the 21stCentury in prospect[J]. Progress in Geophysics, 2001, (5): 345～352.

[21] 曲寿利,季玉新,王鑫,等. 全方位P波属性裂缝检测方法[J].石油地球物理勘探,2001,36(4):390～397.

QU Shou-li, JI Yu-xin, WANG Xin, et al. Seismic method for using full-azimuth P wave attribution to detect fracture[J]. Oil Geophysical Prospecting, 2001, 36(4): 390～397.

[22] 滕吉文，王光杰，杨顶辉，等，地球各向异性介质中地震波动理论、检测与应用研究[J].地学前缘，1998，5(1):83～90.

TENG Ji-wen, WANG Guang-jie, YANG Ding-hui, et al. The study for propagation theory of seismic waves, detection technique and application on anisotropic media in the earth′s interior[J]. Earth Science Frontiers, 1998,5(1):83～90.

[23] Thomsen L. Weak elastic anisotropy[J].Geophysics, 1986,51:1954～1966.

[24] Thomsen L. Weak anisotropic reflections[C]//Castagna J P, Backus M M. Offset dependent eflectivity. SEG，1993.

[25] Thomsen L. Elastic anisotropy due to aligned cracks in porous rock[J]. Geophysical Prospecting, 1995,43: 805～829.

STUDY ON SEISMIC PROPERTY OF CRACK-INCLUDED PHYSICAL MODEL

ZHAO Wei-hua1,2, WEI Jian-xin3, SUN Dong-sheng1,2, LI A-wei1,2, WANG Hong-cai1,2

(1.InstituteofGeomechanics,CAGS,Beijing100081,China; 2.KeyLaboratoryofNeotectonicMovementandGeohazard,MinistryofLandandResources,Beijing100081,China;3.CNPCKeyLabofGeophysicalProspecting,ChinaUniversityofPetroleum,ChangpingDistrict,Beijing, 102249,China)

It is very helpful in petroleum production, groundwater exploration and to disposal of pollution to investigate the seismic property of the crustal rocks included cracks or fractures. Two group physical models with the same diameter varying crack density and the same density varying diameters were constructed. The seismic velocities were measured under different confining pressure and calculated by numerical simulation based on Hudson theory. The calculated and measured results show that theVpandVsnearly increase linearity and there anisotropy keep nearly stable constant with confining pressure.Vpcircles decrease with the crack density varying from 2% to 6%. Moreover, the slowVpdecrease more amplitude than the fastVpwhich maintains nearly stable, theVpandVsanisotropy all increase with the crack density ranging from 2% to 6%.With the crack diameter varying from 2 mm to 3 mm, theVpincreases, but theVpanisotropy decreases,Vsand theVsanisotropy nearly remain constant. Comparing the experimental and the theoretical calculated results, new conclusion of Hudson theory used in different depth was discussed, and the primary constraint of its application were analyzed. It is very helpful in petroleum production, exploration of groundwater and disposal of pollution to investigaste the seismic property of the crustal rocks with cracks or fractures.

crack; Hudson theory; rock physical model; velocity; confining pressure

1006-6616(2016)04-0967-09

2016-06-20

中国地质调查局地质调查项目“特殊地质地貌区填图试点”(DD20160060)

赵卫华(1984-)，男，硕士，主要从事岩石物理学、岩石力学及地应力等研究工作。E-mail:weihuazhao@163.com

P315.3

A