第二十一届国际天文奥林匹克竞赛理论试题详解
2016-03-07□李昕
□ 李 昕
第二十一届国际天文奥林匹克竞赛理论试题详解
□ 李 昕
本届国际天文奥林匹克竞赛的理论环节高、低年组各5道题,每题8分,总分40分。同学们完全可以不按试卷上给的题号顺序答题,建议通读一遍题目后,挑选容易有思路的题目开始作答。
α-1火星卫星
首先,如题意要在火星的人造卫星上看到与地球情况相同的日食,就是要让卫星与火星所处的距离恰好能使火星与太阳的角直径相同。设卫星与火星距离为A,火星与太阳距离为L,太阳和火星的直径分别为D和d。为使角直径相同需满足:d/A=D/(L+A),查表代入已知数据可解得A≈1.11×108km。
有的同学认为到这里本题已经作答完毕,实际上这里的分值只有1分。本题的关键是要讨论是否会有距离火星如此远的卫星。为此我们计算火星的第二拉格朗日点位置,卫星如果比L2点还远,火星的引力就将无法束缚它。设其距离火星Λ,有GMS/(L+Λ)2+GMM/Λ2=ω2(L+Λ),其中MS和MM分别为太阳和火星质量,ω为卫星角速度,同时也是火星公转角速度;上式解起来比较复杂,尤其是对低年组的同学,但我们可以将其化繁为简。由于有MS>>MM,L>>Λ,因此GMS/L2=ω2L,ω2=GMS/L3,再代入原式即有:MS/(L+Λ)2+MM/Λ2=MS(L+Λ) /L3;Λ=L×(MM/3MS)1/3=1.08×108km。
可见A>Λ,因此卫星已经超过了火星L2点,不能再作为它的卫星,这种情况也就不可能成立。最后不要忘记用英文写上:impossible situation,此题才能得到满分。
β-1戴森球
我们都知道行星绕中心恒星的公转周期仅与中心恒星的质量和轨道半径有关。即t=2π/ω,ω2R=GM/R2。
题目中说行星就是在参宿四表面上运行,因此这里面的R即是轨道半径,又是恒星的半径,这道题的重点就是求参宿四的半径。
根据斯特藩·玻尔兹曼定律我们可知L~R2T4,我们可以引入太阳的数据求出参宿四的半径。其中太阳半径R⊙、表面温度T⊙、参宿四的表面温度TB,以及两者的质量都可以从常数表查得。光度L虽然不能直接查得,但可以通过视星等(0.5m)和距离(197pc)来计算。
根据距离模数公式:m-M=5logD-5,可以计算出参宿四与太阳的绝对星等差Δm=10.8m,因此有:LB/ L⊙=100Δm/5=21000。
根据已知条件,我们就可以求出R=(21000)1/2R⊙(T⊙/ TB)2。
再计算出t≈247天。
考虑到这种计算周期的方法是估算,因此结果不能这么精确,大约是250天,这个粗略的结果占1分,如果你的结果过于精确的话就不能得到这1分了。
α-2一天的长度
本题提出了一个很有趣的问题,地球两极冰川的消融导致海平面上升,从而使自转变慢。
地球自转满足角动量L守恒,我们可以将其写成L0=I0·ω0=(2/5M0R2+Iice)ω0,其中I是转动惯量,常数表里有固体球转动惯量公式,ω是角速度;当一部分冰融化以后,地球半径增加了Δh,角动量:L1=I1ω1=(2/5M0R2+2/3ηρSΔh(R+Δh/2)2) ω1,其中的S为地球表面积,ρ为海水的密度,η为海洋占地球表面积的百分比,这里可以取0.7,当然±0.05都算正确。
那么ηρSΔh就是冰融化导致的海平面升高所产生的质量,由于Δh<<R,上式最后那部分的(R+Δh/2)2可以近似为R2。
由于动量守恒,即L0=L1,因此有:(2/5M0R2+Iice) ω0=(2/5M0R2+2/3ηρSΔhR2) ω1。
冰融化前主要是在两极地区,因此Iice也是极小量,可以忽略。又有ω=2π/T,这里的T就是地球自转周期。于是我们可以得到:8/3πηρR4Δh (2π/T1)= 2/5M0R2(2π/T0-2π/T1)= 2/5M0R22π(T1-T0)/T1T0。
由于T1≈T0≈T,有:8/3πηρR4Δh=2/5M0R2ΔT/T,代入所有已知数据可得Δh/ΔT=0.11m/ms。
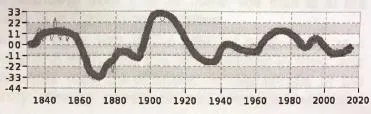
从图中可测量出1995年到2003年每天的长度缩短了1.8ms,因此海平面降低了0.2米。
β-2一天的长度
本题解法与α-2基本相同,找到Δh与ΔT的关系,根据图中找出每个比较明显的天长变化ΔT,计算出相应的Δh。在找出ΔT时,同学们要考虑到天长变化最长周期的影响因素,即每千年增加16ms。在图中给出的1830年至2014年的将近200年里,这个变化导致天长增加了3.2ms,而这并非是由海平面上升引起的。因此最后画出的纵坐标为Δh的图会比给出的图更向下倾斜,如图所示。
αβ-3 天兆,两颗彗星
3、4两题虽出自一段历史故事,但它们考查的要点完全不同。第3题主要涉及行星轨道和角分辨率的知识。
题中提到两颗彗星的公转周期都是3年,我们立刻想到根据开普勒第三定律T2/a3=1,可以计算出其轨道半长径a=2.08au。
又有彗星远日点位于小行星带中间位置,我们可以回忆谷神星就在小行星带中间位置,它到太阳的平均距离大约是2.8au,当然数据表里也有。那么彗星的近日点就在2a-2.8=1.36au的位置。
题中还有一个重要的已知条件,即彗星位于远日点时正好相对地球冲日,也就是说彗星、地球和太阳在一条直线上。那么近日点时,也就是半个公转周期,即1.5年以后,它依然相对地球冲日。因此远日点时它与地球相距1.8au,近日点时为0.36au。
接下来讨论两颗彗星之间的距离,设其远日点时距离为LA,近日点时为LP。根据开普勒第二定律有:LA×1.8au=LP×0.36au,也就是另一种形式上的单位时间扫过的面积相等。
远日点时,两颗彗星在肉眼看上去恰好是一个点,我们人眼的分辨率大概是1′。
最后在两个三角形中,我们就可以解出近日点期间两颗彗星的角距离大约是7′。
αβ-4天兆,月亮和彗星
本题一看就是要进行日期的精确计算,因为子问题中涉及了月球在哪个星座,上一届IAO也考了类似的问题。
4.1 题中说彗星从月牙的亮面出来。我们都知道月球相对背景星空的自行是由西向东,而且肯定比彗星自行得快。除非彗星距离地球比月球还要近,但根据题意这是不可能的。因此如果彗星从亮面出现肯定是蛾眉月的月相,那么一定是在日落后的黄昏时段看到这一天象。
4.2 题中提到月相是非常细的月牙,因此也就是农历初二或者初三前后,即月球位于太阳东侧30°左右。题中说的观测日期大约是6月22日,这段时间太阳位于金牛座,那么月球应该位于双子座。
4.3 根据题中几支军队的地理位置,拜占庭的军队被包围在君士坦丁堡,保加利亚军队位于西北方,希腊军队位于东南方。这时候大家需要把脑洞打开到无限大。夏至前后的日落会在西北方,日落后的月亮和彗星也会位于相近的方位。古人对彗星非常恐惧,认为彗星是不祥之兆。希腊军队面向西北,看到这个天象自然会很害怕。保加利亚军队也会很害怕,因为他们的背后出现了“刀光剑影”。
4.4 图片的艺术性在这里不进行讨论,但图中需要标明方位,以及月球的角直径等信息。
4.5 这是本题中占分值最大的一部分。要想知道看到这一天象是哪天,必须根据之前得到的月相进行精确计算。我们知道最近的一个初三是2016年10月3日(如果你看了月亮应该会知道),当然记得9月1日有日食的话也能推断出。接下来计算其到公元813年一共有多少天。
我们知道每年有365天,4年一个闰年有366天,每逢整百的年份不置闰,但400的整数年份又是闰年。因此有:天数N=(2016-813)×365+int[(2016-813)/4]-9+103,103是10月3日与6月22日相差的天数。
有一个重要的问题,上述的置闰规则是对应新的格利高里历,但在旧历法儒略历转化为格利高里历的1582年实际上少了10天(1582年10月5日被人为规定为10月15日),所以有的同学认为应该减去这10天,其实不然。我们在计算时就是在用格利高里历算的,就不用再去考虑这10天的问题了,大家可以再思考一下原因。
上面求得的N=439490。接下来我们计算这么多天相当于多少个朔望月,有些同学直接拿29.5或者29.53来计算,其实是不正确的。因为在很多天里,朔望月周期取值的不精确会造成很大的误差。在这大约14883个朔望月里,周期取值相差0.005,就会差出大约74天。因此我们要计算更精确的朔望月周期。
在数据表中可以查到月球公转周期是27.3217天,恒星年是365.25636天,它们的会合周期就是朔望月,因此有T=T1T2/ (T2-T1)=29.5306天。因此有439490/29.5306=14882.47个朔望月。由此我们可以推断出观测到该天象的日期是6月22日之前的14天,大约是6月8日前后。
本题主要考查对历法知识的精确掌握,农历在我国使用也很广泛,因此应该很占便宜,但同学们普遍作答得不好。
αβ-5寻找小行星
往届的国际天文奥赛中曾经考过类似的题目。有些同学的思路是通过分辨率公式计算望远镜的口径,再求它在柯伊伯带距离上的分辨率。其实这样考虑不够全面,而且也绕了弯路。
我们设望远镜要想“观测到”小行星或者柯伊伯带天体,接收到的光通量是φ。很容易知道φ与天体光度L成正比,与天体到我们的距离D的平方成反比。但小行星不一样,它们本身不发光,而是反射太阳光,实际上它们的光度L与其表面积(直径d的平方)成正比,与其表面反照率α成正比,与它们到太阳的距离R的平方成反比。因此有:φ~R-2D-2d2α。
同样都是“观测到”,所以φ1=φ2,所以我们找到上述参数的关系就可以求出d2了。
小行星主带和柯伊伯带天体到太阳的距离R分别为2.8au(这个必须记住)和35au~50au(行星数据表里能查到,但也应该记住)。
那么它们到我们的距离D就是上述取值再减1au。
反照率α也可以分别从数据表中查出,谷神星是0.09,Eris是0.9,Makemake是0.77,柯伊伯带天体的反照率可以取两者的平均值。但经过领队讨论,这里只要考虑反照率因素,无论取值多少都给了分。
最后代入所有数据,d1=2.5km,可以计算出d2大约是300km,当然本题也是估算,最后答案的数值如果太精确也是得不到最后的1分的。
(责任编辑 冯翀)
