无侧移半刚性连接箱式模块化框架的稳定分析

曹轲+李国强+陆烨

摘要：基于《钢结构设计规范》（GB 50017—2003），利用三柱子框架模型推导了无侧移半刚性连接箱式模块化框架柱计算长度系数方程，给出了基于分析假定的柱计算长度系数理论解，提出了针对无侧移半刚性连接箱式模块化框架柱计算长度系数的实用计算公式；通过对比理论计算结果和有限元分析结果，验证了实用计算公式的精确性与适用性；研究了无侧移半刚性连接箱式模块化框架柱计算长度系数的各影响因素。结果表明：柱计算长度系数除了受到半刚性节点刚度变化的影响外，还受到上下相邻模块框架梁对框架柱约束系数比值的影响；当上下相邻模块框架梁对框架柱约束系数的比值均为1时，柱计算长度系数不随节点刚度变化而变化。

关键词：计算长度系数；稳定分析；半刚性连接；无侧移箱式模块化框架

中图分类号：TU323.5文献标志码：A

Stability Analysis of Nonsway Modular Frame with Semirigid ConnectionCAO Ke1， LI Guoqiang1，2， LU Ye1，2

（1. College of Civil Engineering， Tongji University， Shanghai 200092， China； 2. State Key Laboratory for

Disaster Reduction in Civil Engineering， Tongji University， Shanghai 200092， China）Abstract： Based on Code for Design of Steel Structures（GB 50017—2003） and using the three column subassemblage model， a governing equation for determining the effective length factor of column for nonsway modular frame with semirigid connection was derived. Furthermore， the theoretical solution to evaluate the corresponding column effective length factor was proposed. The effectiveness and accuracy of the simplified calculation formulas were illustrated through comparing the theoretical calculation results and finite element analysis results. At last， influencing factors of effective length factor of column for nonsway modular frame with semirigid connection were investigated. The results show that the effective length factor is affected not only by the connection stiffness but also by the ratio of modified relative stiffness factor. When the ratio of modified relative stiffness factor is 1， the effective length factor doesnt change with connection stiffness.

Key words： effective length factor； stability analysis； semirigid connection； nonsway modular frame

0引言

箱式模块化钢结构建筑是预制装配式钢结构建筑的一种具体形式，它是将单个房间作为预制单元，在工厂预制后运到工地进行现场安装。每一个预制单元可为带有采暖、给排水及照明等所有管网的装修完备的房间单元。作为集成化程度很高的预制装配式建筑，箱式模块化建筑已经成为新型建筑技术的主要发展方向之一[1]。

目前针对钢框架的研究与设计中常把梁、柱间连接假定为理想的刚接或铰接，然而实际工程中大多数连接介于两者之间，为半刚性连接[2]。普通的半刚性连接是指框架中梁、柱间连接节点为半刚性节点。对于箱式模块化钢结构，在同一模块箱体内部，梁、柱连接采用全焊接连接，而不同箱体之间则采用螺栓节点连接。因此，对于箱式模块化钢框架，同一箱体内梁、柱刚性连接，不同箱体间半刚性连接。

稳定性的设计一直是多层多跨钢框架设计的重要组成部分[3]。目前设计多层多跨钢框架有2种方法：一种是传统的构件计算长度设计法；另一种是高等分析法。各国针对钢框架整体稳定性的设计仍采用第1种方法，因此，框架结构的稳定问题就转化成了柱计算长度的计算问题。目前研究与设计中确定柱计算长度的实用方法是子结构法和层刚度法[4]。对于半刚性节点，国外学者普遍采用转动弹簧模拟节点的半刚性性能，以研究半刚性钢框架柱的计算长度取值问题。依据此种方法，Hellesland等[5]、White等[6]和Kishi等[7]对半刚性连接钢框架柱的计算长度系数进行了研究。随着钢结构在中国的发展和应用，针对半刚性连接钢框架稳定问题的研究逐渐增多，陈绍蕃[3]、陈骥[8]和李国强等[910]针对半刚性连接钢框架的稳定问题进行了研究。

上述研究均针对梁、柱半刚性连接钢框架进行，对于半刚性连接箱式模块化钢框架的整体稳定问题，目前各国尚无研究报道。本文采用《钢结构设计规范》（GB 50017—2003）[11]中的方法，利用子结构模型，推导无侧移半刚性连接箱式模块化框架柱的计算长度系数方程，给出计算长度系数的简化计算公式，并通过对比有限元分析结果验证该简化计算公式的精确性。同时，本文还将分析无侧移半刚性连接箱式模块化框架柱计算长度系数的影响因素。

1分析假定

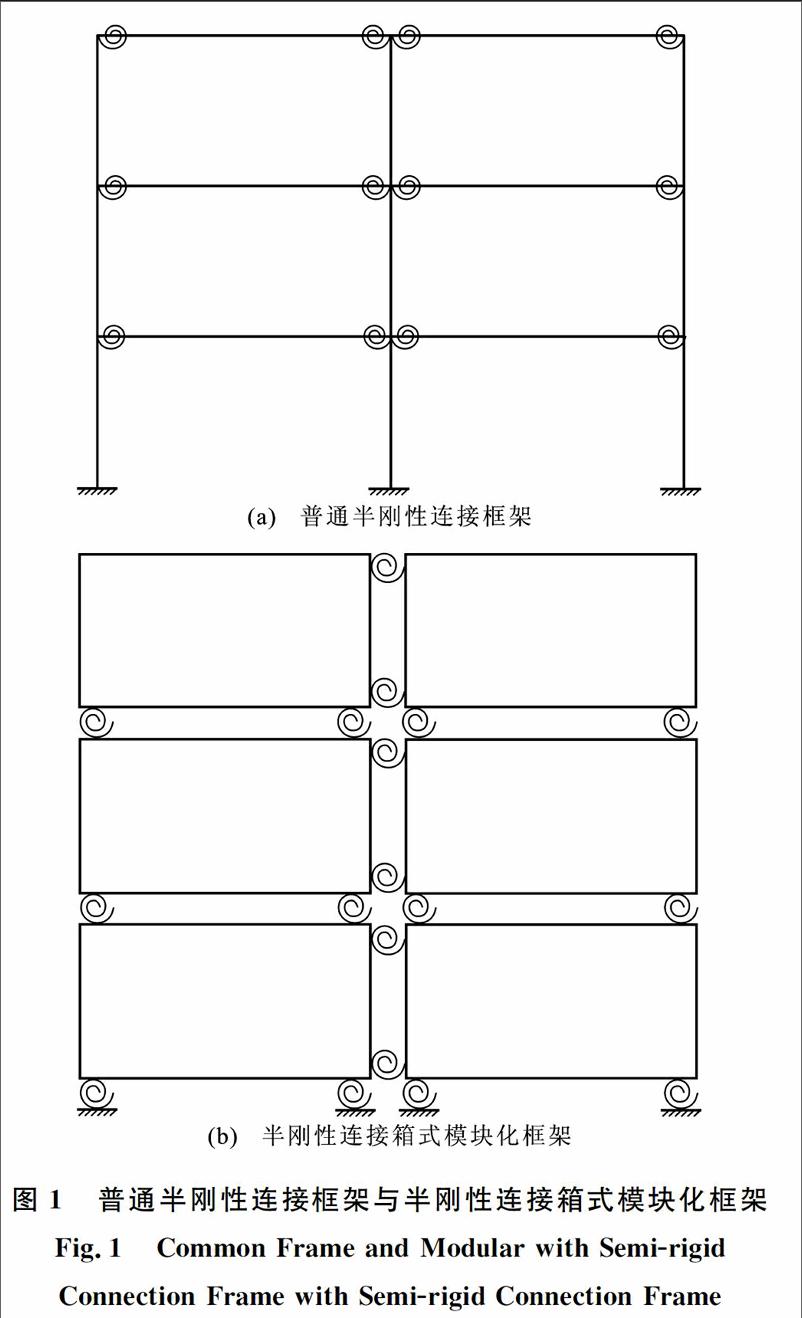
普通半刚性连接框架与半刚性箱式模块化框架见图1。由图1可知，箱式模块化框架结构形式与普通钢框架差异较大，因此在箱式模块化钢框架的设计中不能完全套用普通钢框架的设计方法，而应考虑箱体间连接节点对框架柱稳定性的影响。

图1普通半刚性连接框架与半刚性连接箱式模块化框架

Fig.1Common Frame and Modular with Semirigid

Connection Frame with Semirigid Connection Frame参考《钢结构设计规范》（GB 50017—2003）[11]中关于普通无侧移钢框架柱计算长度系数的有关假定以及文献[7]中针对梁、柱半刚性连接无侧移钢框架柱稳定性分析的有关假定，本文采用以下分析假定：

（1）子框架模型中所有杆件材料均为完全弹性。

（2）所有梁、柱均为等截面形式。

（3）梁内轴力较小，可以忽略。

（4）同层中各柱将同时屈曲，不考虑同层各柱之间的相互影响。

（5）子框架模型中所有柱稳定函数一致。

（6）子框架屈曲时，各梁近端及远端的转角大小相等，方向相反，即各梁按单向曲率弯曲。

（7）同一模块内梁、柱连接为刚性连接，不同模块间连接为半刚性连接。

（8）不同模块间连接节点的半刚性性能用具有一定转动刚度的转动弹簧模拟。

（9）子框架模型中上下相邻柱变形曲线相似，即各柱柱端转角对应成比例。

包含无侧移半刚性连接箱式模块化框架的任一柱CD及所有与柱CD相连构件的子框架模型如图2（a）所示，其中，P为子框架所受轴压力，θ为节点转角，bi（i=1，2，3，4），cj（j=1，2，3）分别为各梁、柱编号。根据分析假定（4），同层中各柱变形相同，故柱MN与柱CD不会产生相对转动，柱MN对柱CD的稳定系数没有影响，可将无侧移模块化子框架模型简化，如图2（b）所示，其中，θA，θB，θC，θD，θE，θF，θG，θH，θI，θJ均为转角，R1，R2均为半刚性节点的转动刚度。该子框架模型与传统的三柱子框架模型类似[8]，包括柱c2[图2（b）中的柱CD]，2根约束柱c1，c3，4根约束梁b1，b2，b3，b4。相同模块内梁、柱均为刚性连接，相邻模块间为半刚性连接。

图2无侧移箱式模块化子框架模型及其简化模型

Fig.2Subassemblage Model for Nonsway Modular

Frame and Its Simplification Model2转角位移方程

由于半刚性连接箱式模块化框架中模块内梁、柱均为刚性连接，节点的半刚性性能只在不同模块间体现，故针对单个构件而言，构件的转角位移方程与普通多层多跨钢框架相同。

按照分析假定（3），框架梁只承受端弯矩作用，如图3（a）所示，其转角位移方程为[2]

MA=kbLb（4θA-2θB）（1）

式中：MA为梁A端弯矩；kb为子框架梁抗弯刚度；Lb为子框架梁跨度。

由分析假定（6）可知，梁发生单向曲率弯曲变形，即θA=θB[图3（a）]，则梁A端弯矩可表示为

MA=2kbLbθA（2）

无侧移子框架中框架柱受轴力及端弯矩共同作用，如图3（b）所示，其中，MB为梁B端弯矩，Lc为子框架柱长度），此时框架梁、柱的转角位移方程可用稳定函数表示为[2]

MA=kcLc（siiθC+sijθD）（3）

MB=kcLc（sjiθC+sjjθD）（4）

sii=sjj=kLcsin（kLc）-（kLc）2cos（kLc）2-2cos（kLc）-kLcsin（kLc）（5）

sij=sji=（kL）2c-kLcsin（kLc）2-2cos（kLc）-kLcsin（kLc）（6）

k=Pkc（7）

图3无侧移箱式模块化框架梁、柱单元转角位移模型

Fig.3Slopedeflection Model of Beam Element and

Column Element for Nonsway Modular Frame式中：kc为子框架柱抗弯刚度；sii，sij，sji，sjj均为稳定函数。

柱计算长度系数μ可表示为

μ=πkLc（8）

将式（8）代入式（5），（6），可得由柱计算长度系数μ表示的稳定函数[8]为

sii=sjj=（π/μ）sin（π/μ）-（π/μ）2cos（π/μ）2-2cos（π/μ）-（π/μ）sin（π/μ）（9）

sij=sji=（π/μ）2-（π/μ）sin（π/μ）2-2cos（π/μ）-（π/μ）sin（π/μ）（10）3柱计算长度系数的计算方程

根据分析假定，子框架屈曲时各梁、柱的转角如图2（b）所示，其中，柱CD为目标柱，柱CD端转角分别为θC，θD，梁CH两端转角θC=θH，梁DI两端转角θD=θI；假定半刚性节点的转动刚度为R1，R2，节点内弯矩分别为MB，ME，则柱AB的B端转角θB=θC-MB/R1，梁BG两端转角θB=θG=θC-MB/R1；同理，柱EF的E端转角θE=θD-ME/R2，梁EJ两端转角θE=θJ=θD-ME/R2；由分析假定（9）可知，柱AB的A端转角θA=（θC-MB/R1）θD/θC，柱EF的F端转角θF=（θD-ME/R2）θC/θD。

引入构件线刚度i′，则有

i′=k0L（11）

式中：k0为构件抗弯刚度；L为构件长度。

当子框架屈曲时，各杆件端部的转角位移方程可表示为

MBG=2ib1（θC-MBR1）（12）

MCH=2ib2θC（13）

MDI=2ib3θD（14）

MEJ=2ib4（θD-MER2）（15）

MBA=ic1[sii（θC-MBR1）+sij（θD-MBθDR1θC）]（16）

MCD=ic2（siiθC+sijθD）（17）

MDC=ic2（siiθD+sijθC）（18）

MEF=ic3[sii（θD-MER2）+sij（θC-MER2θCθD）]（19）

式中：ib1，ib2，ib3，ib4分别为梁b1，b2，b3，b4的线刚度；ic1，ic2，ic3分别为柱c1，c2，c3的线刚度。

由节点B的平衡条件可得

MB=MBA+MBG（20）

将式（12），（16）代入式（20），有

MB=R1θC[（siiic1+2ib1）θC+sijic1θD]R1θC+（siiic1+2ib1）θC+sijic1θD（21）

由节点C的平衡条件可得

MB+MCH+MCD=0（22）

将式（13），（17），（21）代入式（22），有

（siiR1ic1+2R1ib1+2R1ib2+2siiic1ib2+

4ib1ib2+siiR1ic2+s2iiic1ic2+2siiib1ic2）θ2C+

（sijR1ic1+2sijib2ic1+2siisijic1ic2+sijR1ic2+

2sijib1ic2）θCθD+s2ijic1ic2θ2D=0（23）

同理，由节点E的平衡条件可得

ME=MEF+MEJ（24）

将式（15），（19）代入式（25），有

ME=R2θD[（siiic3+2ib4）θD+sijic3θC]R2θD+（siiic3+2ib4）θD+sijic3θC（25）

由节点D的平衡条件可得

ME=MDI+MDC=0（26）

将式（14），（18），（25）代入式（26），有

（siiR2ic3+2R2ib4+2R2ib3+2siiib3ic3+

4ib3ib4+siiR2ic2+s2iiic2ic3+2siiib4ic2）θ2D+

（sijR2ic3+2sijic3ib3+2siisijic2ic3+sijR2ic2+

2sijib4ic2）θCθD+s2ijic2ic3θ2C=0（27）

引入框架梁对框架柱的约束系数Ki（i=1，2，3，4）及半刚性节点对框架柱的约束系数Ji（i=1，2，3，4），有

K1=ib1ic1，K2=ib2ic2，K3=ib3ic2，K4=ib4ic3（28）

J1=R1ic1，J2=R1ic2，J3=R2ic2，J4=R2ic3（29）

将式（28），（29）代入式（23），（27），有

（siiJ2+2J2K1+2J1K2+2siiK2+4K1K2+

siiJ1+s2ii+2siiK1）θ2C+（sijJ2+2sijK2+

2siisij+sijJ1+2sijK1）θCθD+s2ijθ2D=0（30）

（siiJ3+2J3K4+2J4K3+2siiK3+4K3K4+

siiJ4+s2ii+2siiK4）θ2D+（sijJ3+2sijK3+

2siisij+sijJ4+2sijK4）θCθD+s2ijθ2C=0（31）

式（30），（31）为只含二次项的二元二次方程组，可采用因式分解进行简化，令

（θC+α1θD）（α2θC+α3θD）=0（32）

将式（32）代入式（30），有

α2=siiJ2+2J2K1+2J1K2+2siiK2+4K1K2+

siiJ1+s2ii+2siiK1（33）

α1α3=s2ij（34）

α1α2+α3=sijJ2+2sijK2+

2siisij+sijJ1+2sijK1（35）

同理，令

（α4θC+θD）（α5θC+α6θD）=0（36）

将式（36）代入式（31），有

α6=siiJ3+2J3K4+2J4K3+2siiK3+4K3K4+

siiJ4+s2ii+2siiK4（37）

α4α5=s2ij（38）

α4α6+α5=sijJ3+2sijK3+

2siisij+sijJ4+2sijK4（39）

联立式（32），（36），并引入边界条件0.5<μ<1，可得满足条件的屈曲方程为

detα2α3

α5α6=0（40）

将计算所得α1，α2，…，α6代入式（40），有

{s2ii+2[J2K1+（J1+2K1）K2]+sii[J1+J2+

2（K1+K2）]}{s2ii+2[J4K3+（J3+2K3）K4]+

sii[J3+J4+2（K3+K4）]}-14s2ij[2sii+J1+J2+

2（K1+K2）+[J21+2J1（J2+2K1-2K2）+（J2-

2K1+2K2）2]1/2[2sii+J3+J4+2（K3+K4）+

[J23+2J3（J4+2K3-2K4）+（J4-2K3+

2K4）2]1/2=0（41）

将式（9），（10）代入式（41），即可得到关于柱计算长度系数μ的计算公式。4柱计算长度系数的简化计算公式

对于梁、柱刚接无侧移多层多跨框架柱，各国较为通用的实用柱计算长度系数公式为[8]

μ=0.64K1K2+1.4（K1+K2）+31.28K1K2+2（K1+K2）+3（42）

柱计算长度系数公式最早于1966年被法国钢结构设计规范所采用[12]。1978年，欧洲钢结构协会将其列入了欧洲钢结构规范。Dumonteil[13]指出该公式不仅足够精确，而且便于电算。中国规范[14]也将该公式作为确定框架柱计算长度系数的推荐公式。

对于无侧移半刚性连接箱式模块化子框架，当半刚性连接转动刚度很大时，可认为节点刚接，此时柱的计算长度系数可采用式（42）计算，其中

K1=ib1+ib2ic1+ic2（43）

K2=ib3+ib4ic2+ic3（44）

式（43），（44）为无侧移半刚性连接箱式模块化框架柱的边界条件，当半刚性连接转动刚度R1，R2足够大时，无侧移半刚性连接箱式模块化框架柱计算长度系数的简化计算公式应该能回归到式（42）的形式。

根据上述分析，无侧移半刚性连接箱式模块化框架柱计算长度系数的简化计算公式如下

μ=0.64K′1K′2+1.4（K′1+K′2）+31.28K′1K′2+2（K′1+K′2）+3（45）

K′1=J2K1+（J1+α）K2J2+J1+α（46）

K′2=J3K4+（J4+α）K3J3+J4+α（47）

式中：K′1，K′2均为修正的柱端约束参数；α为待定常数。

当半刚性连接转动刚度R1，R2足够大时，可认为节点刚接，此时R1，R2为等阶无穷大，式（46），（47）可退化为式（43），（44）。

通过式（41）得到的柱计算长度系数方程为超越方程，可通过数学软件求出其数值解；通过实用柱计算长度系数公式求得的柱计算长度系数为μ′，采用最小二乘法，使得μ′与μ相对误差最小，可求得待定常数α的取值为0.2。针对几种常见Ki，Ji（i=1，2，3，4）值，μ，μ′及其相对误差见表1。实用柱计算长度系数公式所得值与理论公式所得值相对误差均值为-1.19%。表1柱计算长度系数的理论值、实用公式值与有限元值对比

Tab.1Comparison of Effective Length Factors of Columns Between Theoretical Results， Simplified Formulas

Results and Finite Element Results编号影响因素K1K2K3K4J1J2J3J4μμ′μ″μ′-μμ/%μ″-μμ/%10.20.60.60.60.750.750.750.750.861 80.855 40.819 8-0.740 8-4.870 720.40.60.80.20.504.005.002.000.880 60.877 30.842 1-0.370 0-4.376 030.60.40.81.04.000.250.753.000.834 20.836 70.799 70.296 6-4.138 5 40.80.40.62.03.002.005.001.000.774 50.774 50.723 0-0.001 7-6.644 0 51.00.41.50.22.005.001.004.000.781 60.775 70.733 9-0.758 5-6.099 7 61.50.41.00.65.001.004.000.250.839 60.836 30.810 7-0.394 7-3.447 3 72.00.81.52.50.502.000.750.250.711 10.698 80.676 6-1.734 2-4.847 482.50.42.02.50.250.753.002.000.736 40.693 60.735 7-5.818 4-0.088 9注：μ″为有限元模型所得柱计算长度系数。5柱计算长度系数的数值验证

为验证无侧移半刚性连接箱式模块化框架柱稳定分析的正确性，采用有限元分析软件SAP2000建立如图4（a）所示的5层框架模型，层高为3 m，长边方向跨度为6 m，短边方向跨度为2.4 m，梁、柱最大划分长度为0.1 m。梁采用槽钢截面，柱采用方钢管截面，底部柱脚刚接。文献[7]在梁、柱半刚性连接无侧移框架柱的计算长度系数推导中考虑了半刚性节点的非线性弯矩转角关系模型，指出竖向荷载作用下节点内部可能已经存在较大转角，使得半刚性节点的实际刚度小于初始刚度。对于模块化钢框架，在竖向荷载作用下，上下相邻模块间的相对转角很小，半刚性连接内的弯矩可忽略不计，故本文直接采用半刚性节点的初始刚度进行计算。模块间连接采用线性弹簧模拟，约束弹簧X，Y，Z方向的平动自由度以及弹簧X，Y方向的转动刚度按实际连接节点的初始刚度取值。毛磊[15]针对一种常用的模块箱体连接节点进行了节点试验，得到该种节点的初始转动刚度为4 930 kN·m·rad-1，有限元模型中按照该值进行计算。约束框架顶层柱柱顶节点沿X，Y方向的转动自由度与平动自由度，约束框架底层柱柱底节点沿X，Y方向的转动自由度与沿X，Y，Z方向的平动自由度，使得整个框架的屈曲主要集中在中间3层。为模拟无侧移条件，约束各梁、柱节点沿X，Y方向的平动自由度。在框架顶层柱顶端施加单位竖向荷载，对框架进行特征值屈曲分析，分析时刚度采用零初始条件零预应力状态，特征值收敛容差为1×10-9。

模型屈曲变形如图4（b）所示。从图4（b）可见，框架的1阶屈曲模态与理论推导中所假设的子框架变形模态基本一致，且符合理论推导中的各分析假定。由有限元软件所得柱计算长度系数μ″及其与μ的相对误差见表1。有限元模型所得结果与理论公式所得结果的相对误差均值为-4.31%。

图4有限元模型及其屈曲变形

Fig.4Finite Element Model and Its Buckling Deformation从图4和表1可以看出，各柱实际变形与理论假设并不完全一致，且有限元模型所得柱计算长度系数较理论值普遍偏小，这是由于理论计算采用的子框架模型假设各柱变形曲线相似，同时整个分析模型上下完全对称。有限元模型中框架顶层、底层柱远端约束，且顶柱、底柱约束并不完全相同，这导致了整个模型并非完全上下对称，各柱实际变形与理论假设并不完全一致，使得理论计算模型中假定的框架边界约束条件弱于有限元模型。6柱计算长度系数的影响因素

通过定性分析可知，框架柱计算长度系数除了受到半刚性节点对柱约束系数J1，J2，J3，J4的影响以外，还受到框架梁对框架柱约束系数比值K1/K2，K4/K3的影响。当K1/K2，K4/K3均为1时，子框架各柱的柱端约束系数相同，此时子框架屈曲时各柱的柱端转角相同，半刚性节点内的弯矩为0，此时柱计算长度系数不随半刚性连接节点刚度变化而改变，其简化计算公式（45）很好地反映了这一特性。通常无侧移半刚性连接箱式模块化框架中K1/K2，K4/K3并不为1，此时节点转动刚度将会对柱的计算长度系数产生影响。

由子框架的对称性可知，K4/K3对柱计算长度系数的影响与K1/K2完全相同，故假设J1=J2=J3=J4，K1=K3=K4=1，仅改变J1及K2，以研究在不同K1/K2取值情况下J1对框架柱计算长度系数μ的影响，所得结果如图5所示。

图5不同K1/K2情况下μ随J1的变化曲线

Fig.5μJ1 Curves Under Different K1/K2 Cases从图5可知：

（1）当K1/K2=1时，柱计算长度系数μ不随J1的变化而变化，这与定性分析结果一致。

（2）当K1/K2<1时，柱计算长度系数μ随J1的变大而变大并逐渐趋于稳定。这是由于当K1/K2<1时，节点对柱c2的弯矩方向与柱c2变形方向相同，该弯矩使柱c2的临界荷载变小，μ值增大，且该弯矩随节点转动刚度的增大而逐渐增大。反之，当K1/K2>1时，μ随J1的变大而变小并逐渐趋于稳定。

（3）目前在模块化建筑的设计中常忽略模块间连接节点的转动刚度，将其按照铰接节点计算，这种方法可能导致柱计算长度系数偏小，从而高估柱的稳定承载力。7结语

（1）无侧移半刚性连接箱式模块化框架与普通钢框架及梁、柱半刚性连接钢框架有较大差别，针对无侧移半刚性连接箱式模块化钢框架的稳定计算不能直接套用传统的计算方法，而应采用本文提出的方法进行计算。

（2）本文提出的实用柱计算长度系数公式与理论解拟合精度较高，能够较好地替代理论计算方法，简化无侧移半刚性连接箱式模块化框架柱的稳定计算过程。

（3）有限元模型所得计算长度系数较理论值普遍偏小， 这是由于有限元模型中子框架顶层、底层柱远端约束与分析模型并不完全相同导致的。有限元模型所得柱计算长度系数与理论解的相对误差均值为-4.31% ，在合理范围内，证明了理论分析的正确性。

（4）柱计算长度系数除了受到半刚性节点刚度变化影响外，还受到上下相邻模块框架梁对框架柱约束系数比值K1/K2，K4/K3的影响；设计中若忽略模块间连接节点的转动刚度，将其按照铰接节点计算可能会导致柱计算长度系数偏小，从而高估柱的稳定承载力。参考文献：

References：[1]DOUGLAS A B L，SANDBANK H.A History of Prefabrication[M].New York：Arno Press，1972.

[2]CHEN W F，LUI E M.Stability Design of Steel Frames[M].Boca Raton：CRC Press，1991.

[3]陈绍蕃.钢结构稳定设计指南[M].2版.北京：中国建筑工业出版社，2004.

CHEN Shaofan.Guide for Stability Design of Steel Structures[M].2nd ed.Beijing：China Architechture & Building Press，2004.

[4]AISC.Manual of Steel Constructionload and Resistance Factor Design[M].3rd ed.Chicago：AISC，1994.

[5]HELLESLAND J，BJORHOVDE R.Restraint Demand Factors and Effective Lengths of Braced Columns[J].Journal of Structural Engineering，1996，122（10）：12161224.

[6]WHITE D W，HAJJAR J F.Buckling Models and Stability Design of Steel Frames：A Unified Approach[J].Journal of Constructional Steel Research，1997，42（3）：171207.

[7]KISHI N，CHEN W F，GOTO Y，et al.Effective Length Factor of Columns in Flexibly Jointed and Braced Frames[J].Journal of Constructional Steel Research，1998，47（1）：93118.

[8]陈骥.钢结构稳定理论与设计[M].2版.北京：科学出版社，2003.

CHEN Ji.Stability of Steel Structures Theory and Design[M].2nd ed.Beijing：Science Press，2003.

[9]李国强，王静峰.无侧移半刚性连接组合框架的稳定分析：（Ⅱ）连接转动刚度和算例分析[J].力学季刊，2006，27（4）：628634.

LI Guoqiang，WANG Jingfeng.Stability Analysis for Nonsway Composite Frames with Semirigid Joints — Part 2 Connection Rotation Stiffness and Examples Analysis[J].Chinese Quarterly of Mechanics，2006，27（4）：628634.

[10]王静峰，李国强.无侧移半刚性连接组合框架的稳定分析：（Ⅰ）柱的有效长度系数方程[J].力学季刊，2006，27（3）：481488.

WANG Jingfeng，LI Guoqiang.Stability Analysis for Nonsway Composite Frames with Semirigid Joints：Part Ⅰ.Equation of Column Effective Length Factor[J].Chinese Quarterly of Mechanics，2006，27（3）：481488.

[11]GB 50017—2003，钢结构设计规范[S].

GB 50017—2003，Code for Design of Steel Structures[S].

[12]HELLESLAND J.Review and Evaluation of Effective Length Formulas[R].Oslo：University of Oslo，1994.

[13]DUMONTEIL P.Simple Equations for Effective Length Factors[J].Engineering Journal，1992，29（3）：111115.

[14]JGJ 99—98，高层民用建筑钢结构技术规程[S].

JGJ 99—98，Technical Specification for Steel Strucure of Tall Buildings.

[15]毛磊.箱式建筑箱体拼接节点受力性能研究[D].上海：同济大学，2015.

MAO Lei.Research on Joint Mechanical Behavior of Container Architecture[D].Shanghai：Tongji University，2015.