基于蚁群算法的输电塔结构局部优化设计

张卓群+任宗栋+李宏男+李宁+王稳

摘要：提出了一种可同时求解结构截面、拓扑、形状和布局优化问题的基于蚁群算法的输电塔结构局部优化设计方法。在统一所有优化变量的基础上，将4类不同层次的优化问题统一为适用于蚁群算法求解的标准化旅行商问题，再采用MATLAB系统平台实现输电塔结构的优化设计和程序化，并以某实际工程为算例对局部优化方法进行验证。结果表明：提出的方法不仅可以简单高效地求解输电塔结构塔身局部的截面、拓扑、形状和布局优化问题，而且具有非常好的实用性和通用性，有望应用于完整的输电塔结构优化设计中。

关键词：输电塔结构；桁架结构；局部优化设计；蚁群算法；旅行商问题

中图分类号：TU279.7文献标志码：A

Local Optimal Design Method of Transmission Tower Structure

Based on ACO AlgorithmZHANG Zhuoqun1， REN Zongdong1， LI Hongnan2， LI Ning1， WANG Wen1

（1. State Nuclear Electric Power Planning Design & Research Institute， Beijing， 100095， China；

2. Faculty of Infrastructure Engineering， Dalian University of Technology， Dalian 116024， Liaoning， China）Abstract： A new local optimal design method of transmission tower structure， which could apply in crosssection， topology， shape and layout optimization problems， was proposed based on ant colony optimization algorithm. With unifying the multiple type variables into discrete variables， the four optimal problems with different levels were transformed into the standardization traveling salesman problem， and it also was realized in programmed control by MATLAB system， then anactual example was calculated to verify the local optimal design method. The results show that the proposed optimal design method has a good performance in crosssection， topology， shape and layout optimal problem with generality and programmed pattern， and it also has a good application prospect in optimal design of transmission power structure.

Key words： transmission tower structure； truss structure； local optimal design； ant colony optimization； traveling salesman problem

0引言

伴随着中国经济建设的快速发展和人民生产生活耗电量的不断增加，以高电压、大容量、长距离、多分裂、多回路为代表的新型输电塔线路得到了广泛的应用。由于输电塔结构是输电线路的重要组成部分，其安全性和经济性直接关系到线路的运营状况和投资效益，所以如何设计既安全可靠，又经济合理的输电塔结构一直是工程界研究的重点和热点。虽然输电塔结构的材料属性很单一，但是其复杂的结构形式和数量众多的杆件都使得结构的优化设计非常困难。此外，鉴于输电塔结构的成批量设计，结构优化的经济效益体现出明显的累积特性，具有非常大的发展空间。因此，现阶段非常有必要针对输电塔杆塔结构形式、经济指标等方面给予更多的研究和分析，并在此基础上提出一套完整且适用于输电塔结构特性的优化设计方法和流程，为今后输电塔结构优化设计的研究工作和实际应用提供帮助。输电塔优化设计方法最早可追溯到1972年，Sheppard等[1]提出了基于动态规划理论的输电塔优化设计方法，1989年Ghannoum等[2]提出了一种同时考虑铁塔和基础造价的优化设计模型。目前，各国输电塔结构优化设计还主要是针对结构的杆件，即截面优化设计。中国通用的设计软件也基本上是采用了满应力方法进行的杆件截面优选，但是其优化幅度和效果很难达到设计人员的期望。此外，当结构优化层次和难度不断增加时，除了输电塔结构的截面优化设计以外，还要进行输电塔结构的拓扑、形状和布局优化设计。相对于截面优化设计，其余3种优化设计无论在优化空间，还是经济效益方面都具有更高的优化价值。随着近些年来启发式算法的大量涌现，输电塔结构的优化方法得到了广泛的发展，包括：Rajeev等[34]提出了在离散系统下基于遗传算法的输电塔结构优化设计方法；2001年，王藏柱等[5]提出了基于广义变量近似方法的输电塔形状优化方法；2010年，崔磊等[67]提出基于斐波那契搜索、递归方法以及基于递归思想的输电塔结构优化方法；2012年，李林等[8]提出了一种适用于离散变量并考虑压杆稳定性的满应力优化设计方法等。

综上所述，鉴于有限元软件及优化方法的不断发展和完善，以及蚁群算法（Ant Colony Optimization，ACO）在结构优化设计中的良好表现，结合基于蚁群算法的桁架结构离散型变量优化方法，本文归纳总结出了一种基于蚁群算法的完整输电塔结构优化设计方法。

1结构优化设计方法

1.1优化设计模型

输电塔结构优化问题模型[910]简化为

minP=Mi=1ρiAiTiLi（C）pii=1，2，…，M

s.t.

gj（Ai，Ti，C）≤0j=1，2，…，NG

Ai∈S={S1，S2，…，SNS}

Ti=0，1

C=（x1，x2，…，xk，…，xNC），

xk≤xk≤xkk=1，2，…，NC（1）

式中：P为输电塔结构的总价格；ρi，Li，pi分别为单个杆件的密度、长度和造价；Ai为杆件截面设计变量；Ti为结构拓扑设计变量；C为结构形状设计变量；gj为约束函数；S为截面变量离散域；xk，xk分别为节点坐标xk的上限和下限；M为杆件数；NG为约束函数数量；NS为离散截面型号数量；NC为结构形状控制参数数量。

1.2蚁群算法

蚁群算法又称蚂蚁算法[1113]，是由意大利学者Dorigo等于1991年首次提出的。该方法是一种新型的启发式算法，来源于真实的蚂蚁觅食行为，主要采用了分布式并行计算机制，不存在中心控制，是一种全局搜索算法。此外，该算法在求解过程中不严格依赖于问题的数学性，具有很强的适应性、鲁棒性，并具有易于与其他方法相结合等特点。该方法不仅被认为是处理旅行商问题的最优方法之一，而且在离散变量优化问题中也表现出了良好的性能。因此，蚁群算法逐渐被结构优化设计领域所接受，特别是对于基于离散变量且杆件众多的输电塔结构优化设计问题。鉴于旅行商问题是一种通用且表述清晰的数学问题，所以不同层次的输电塔优化问题也都可以转化为不同搜索规模的旅行商问题。因此，采用蚁群算法求解转化后的输电塔结构优化问题不仅可以实现方法的统一性，而且快速高效。

1.3优化设计思路

输电塔结构优化设计的思路就是将不同层次和难度的输电塔结构优化问题转化为同一类或同一种旅行商问题，并且转化的方式和优化准则必须相互一致[14]。存在的问题主要包括2个方面：①不同层次和难度的优化问题如何转化为简单的旅行商问题，以及城市间表达不同优化内容虚拟路径的物理意义；②截面优化变量、拓扑优化变量和形状优化变量如何统一为离散变量。

1.3.1优化问题转化

经典的旅行商问题要求访问者（蚁群）必须依次通过每个城市，且走完所有城市。输电塔结构优化问题的转化同样如此，就是需要将决定结构构件尺寸、决定结构整体拓扑形式和决定结构几何形状的变量转化为不同层次的城市信息，最终采用蚁群算法进行搜索。不同之处在于，传统的旅行商问题中2个城市之间只有1条路径，并且蚂蚁从一个城市可以选择访问任何一个未参观的城市，并且不同城市被选择的概率各不相同。然而输电塔结构优化设计中，2个城市之间包含多条虚拟路径，每条路径代表着某一相同设计变量的不同选择，并且不同城市之间的路径数量并不相同，如图1，2所示。图1中，V为某一优化阶段的优化路径（不同优化阶段代表不同的含义，包括截面、拓扑、形状，下文以截面为例），n为某一优化阶段的某一优化变量所允许的路径，m为某一优化阶段的优化变量数量，V12为截面优化阶段的第1变量允许的第2条路径。虚拟路径长度取决于结构截面面积、拓扑能量和几何形状设计变量的搜索范围和空间，即将不同杆件的截面面积、不同结构形式的拓扑总量、不同几何形状的形状总量都看作不同城市间的路径长度，目标函数（总的结构质量）看作蚂蚁经过的总长度。针对不同层次和难度的优化问题，蚁群所访问的城市是一致的，但是需要搜索的虚拟路径并不相同。简言之，在低层次的输电塔结构优化问题中，部分城市间的路径是惟一的，不再需要搜索。

图1结构优化设计虚拟搜索路径

Fig.1Structure Optimal Design Virtual Search Path图2桁架结构截面优化设计流程

Fig.2Truss Structural Section Optimal Design Flow为了更加清晰明了地说明不同优化内容在优化过程中的物理意义，有必要对这个方面作进一步的说明。旅行商问题实际上是反映了单独路径与路径总长之间的关系，在输电塔结构优化中同样可以建立这种相似的相互关系，并且结构优化内容同样具有各自清晰的含义。具体说明如下：①结构截面优化，单个杆件截面尺寸的选择反映的是单个构件的质量，结构截面尺寸（结构截面总量）的选择反映了结构整体的总质量，即拓扑类型和几何形状一定时，截面尺寸越大，截面总量越大，结构的质量（造价）就越高；②结构拓扑优化，单个杆件拓扑形式的选择反映的是2个节点是否存在杆件的连接，结构的拓扑形式（结构拓扑总量）反映了结构整体的复杂程度，即截面尺寸和几何形状一定时，拓扑总量越大，结构复杂程度越高，结构的质量（造价）就越高；③结构形状优化，单个结构形状变量坐标的确定反映了结构某一部分所占空间的大小，结构整体的几何形状（结构形状总量）反映了结构整体占用空间的大小，即截面尺寸和拓扑类型一定时，形状总量越大，结构空间占用率越高，结构的质量（造价）就越高。

1.3.2优化设计变量

如何将截面优化变量、拓扑优化变量和形状优化变量全部转化为离散变量是蚁群算法能否高效、快速地求解输电塔结构优化设计问题的关键和基础。借鉴相关文献，本文将输电塔结构的截面、拓扑、形状设计变量均转化为离散变量，具体情况如下：①截面优化设计变量，选取结构通常使用的角钢或钢管标准型号，即离散的标准截面尺寸；②拓扑优化设计变量，将输电塔结构任意一个杆件是否存在定义为拓扑量，拓扑总量定义为任意结构形式下全部杆件拓扑量的总和，并采用整数形式的表达方式[15]，因此，在输电塔结构拓扑优化设计中，拓扑总量被定为拓扑优化的设计变量，数值大小看作蚁群路径长度，表示结构的复杂程度；③形状优化设计变量，借鉴基于网格划分策略的连续域蚁群算法的基本思想和基于离散和连续变量的桁架结构形状优化方法的成功经验，本文采用网格划分的方法将不同的形状坐标空间离散化，并根据不同离散点构建的不同结构几何形状定义结构的形状优化设计变量，将其称之为结构形状总量[16]。

输电塔结构不同的设计变量均可以转化为离散变量，而且可以代表旅行商问题转化后的虚拟路径，这表明：采用蚁群算法处理结构优化问题的2类核心问题都被合理地解决，并且蚁群算法的优越性已经在已有文献中得到了验证。此外，文献[6]，[7]，[14]，[16]均表明蚁群算法在求解不同层次桁架结构优化问题时具有明显的优势。因此，蚁群算法可以实现同时处理不同层次和难度的输电塔结构优化设计问题。2优化算例

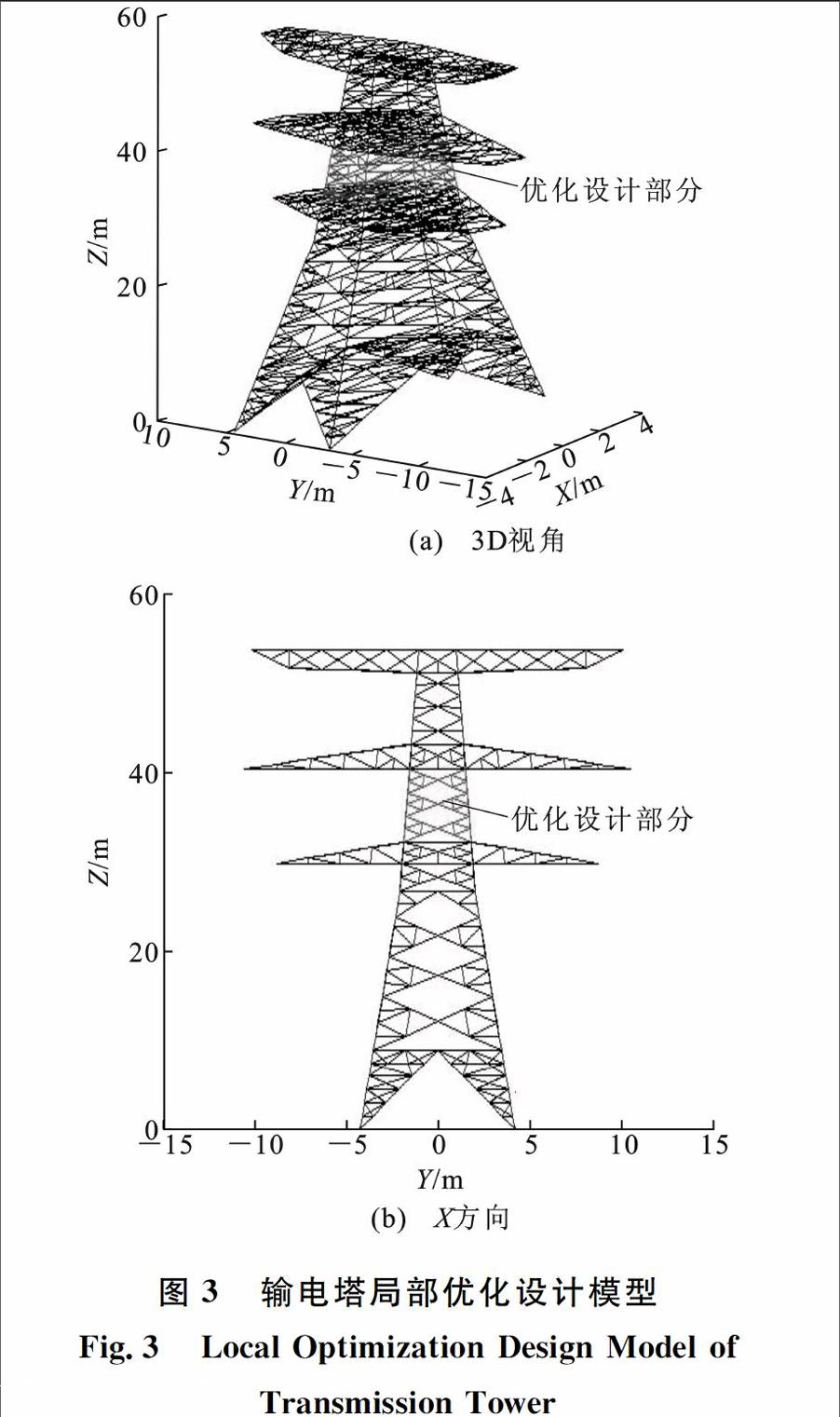
工程背景为辽宁省盖州市境内500 kV新建电渤输电线路一部分，工程起于营口华能电厂，止于盖州500 kV渤海变电所，线路全长35.71 km。输电塔模型为SZ21型直线塔，结构呼高为30 m，塔体总高53.9 m，基础底宽与主塔顶宽分别为8.36 m和2.0 m。输电塔设上、中、下3个横担，由下至上伸臂长度分别为8.7，10.45，10 m。输电塔模型如图3所示，整个铁塔共有639个节点和1 646根杆件单元，钢材采用Q235钢和Q345钢，弹性模量E均为2.1×105 MPa，约束条件参考输电塔结构设计规范[7]。鉴于输电结构杆件众多，形式复杂，以及充分说明蚁群算法在不同优化设计中的良好表现，重点研究了输电塔塔身的一部分。由于不同类型钢材的密度和弹性模量相差不大，为了更好地区分不同钢材的特性，本文的目标函数为工程造价（仅考虑钢材价格，不含钢板、螺栓、垫圈、脚钉、绝缘子串、金具等构件的花费，以及人工费和输电塔结构的构造要求等），并且假设Q235钢为4 200元·t-1，Q345钢为4 500元·t-1（参考2013年底，中国钢材的价格）。铁塔所用角钢规格不宜小于L40×3，局部结构拓扑形式如图4所示，杆件按构件长度和功能划分结构形状变量坐标及其连接情况如图5和表1所示，蚁群参数取值如表2所示。

图3输电塔局部优化设计模型

Fig.3Local Optimization Design Model of

Transmission Tower图4局部结构拓扑形式

Fig.4Topology Forms of Local Structure图5形状优化设计变量

Fig.5Shape Optimal Design Variables2.1截面优化

应用基于蚁群算法的输电塔结构离散变量优化

表1输电塔局部优化设计坐标变量连接情况

Tab.1Local Optimal Design Coordinates Links

Conditions of Transmission Tower节点编号X方向Y方向Z方向1X1Y1Z12X1-Y1Z13-X1-Y1Z1 4-X1Y1Z1节点编号X方向Y方向Z方向5X2Y2Z26X2-Y2Z27-X2-Y2Z28-X2Y2Z2表2输电塔结构蚁群算法控制参数

Tab.2Control Parameters of ACO for

Transmission Tower Structure参数αβρQm′Nmax数值10.20.1130100注：α为路径上残留信息的重要程度，α≥0；β为启发信息的重要

程度，β≥0；Q为表示信息强度的常数；m′为蚁群数量；Nmax

为最大迭代次数。

设计方法对某一既有输电塔局部结构进行截面优化设计，优化部分原始模型如表3所示。本文在MATLAB软件平台上编写了相应的优化设计程序，最终的截面优化设计结果如表4所示，结构造价为87 255元，其中，截面变量为27个，每类杆件可选择的范围为73种。截面优化过程如图6所示。

2.2拓扑优化

应用基于蚁群算法的输电塔结构局部优化设计方法和程序对塔身局部进行拓扑优化设计，拓扑模型如图4所示，蚁群算法参数见表2，其中，截面变量类型与截面优化一致，拓扑模型为64种。拓扑优化设计后的模型如表5所示，拓扑优化设计过程如表3输电塔局部优化设计原始数据

Tab.3Local Optimal Design Initial Data of Transmission Tower优化变量优化变量分类造价/元截面1类（Q345L140×10），2类（Q235L75×6），3类（Q235L40×4），4类（Q235L40×4），5类（Q235L40×4），

6类（Q235L70×6），7类（Q235L40×4），8类（Q235L40×4），9类（Q235L40×4），10类（Q345L140×10），

11类（Q235L70×6），12类（Q235L40×4），13类（Q235L40×4），14类（Q235L40×4），15类（Q235L70×6），

16类（Q235L40×4），17类（Q235L40×4），18类（Q235L40×4），19类（Q345L125×10），20类（Q235L75×6），21类（Q235L40×4），22类（Q235L40×4），23类（Q235L40×4），24类（Q235L75×6），25类（Q235L40×4），

26类（Q235L40×4），27类（Q235L40×4）拓扑拓扑1（类型A），拓扑2（类型A），拓扑3（类型A），拓扑4（类型A），拓扑5（类型A），拓扑6（类型A），

拓扑7（类型A），拓扑8（类型A）形状X1=1.710 m，Y1=1.710 m，Z1=35.200 m，X2=1.610 m，Y2=1.610 m，Z2=37.90088 418表4输电塔局部截面优化设计结果

Tab.4Local Section Optimal Design Results of Transmission Tower优化变量优化变量分类造价/元截面1类（Q345L140×10，2类（Q235L75×5），3类（Q235L36×3），4类（Q235L45×3），5类（Q235L36×3），

6类（Q235L70×4），7类（Q235L36×3），8类（Q235L40×4），9类（Q235L36×3），10类（Q345L125×10），

11类（Q235L70×4），12类（Q235L36×4），13类（Q235L45×3），14类（Q235L36×3），15类（Q235L70×4），

16类（Q235L36×4），17类（Q235L40×5），18类（Q235L40×3），19类（Q345L125×8），20类（Q235L75×5），21类（Q235L40×4），22类（Q235L40×3），23类（Q235L40×3），24类（Q235L70×5），25类（Q235L30×4），

26类（Q235L40×3），27类（Q235L40×3）87 255图6截面优化设计历程

Fig.6Section Optimization Design History图7所示，最终输电塔结构的工程造价为87 464元。

图7拓扑优化设计历程

Fig.7Topology Optimization Design History2.3形状优化

应用基于蚁群算法的输电塔结构局部优化设计方法和程序对塔身局部进行形状优化设计，形状优化变量如图4和表1所示，蚁群算法参数见表2，其中，截面变量类型与截面优化一致，形状变量为6个，网格划分精度为0.2 mm。形状优化设计结果如表6所示，形状优化设计过程如图8所示，最终输电塔结构的工程造价为87 739元。

2.4布局优化

应用本文方法对输电塔塔身部分进行布局优化设计，并采用MATLAB程序进行求解。优化部分原始模型如图3和表3所示，截面、拓扑和形状优化变量如图4，5和表1所示，蚁群算法控制参数如表2所示。布局优化设计结果如表7所示，布局优化设计过程如图9所示，最终的结构造价为87 709元。

2.5优化结果分析

本文采用基于蚁群算法的离散变量优化设计思路对既有输电塔结构的局部进行了优化设计，实现了将不同层次和难度的输电塔结构优化问题转化为统一准则的旅行商问题，并采用蚁群算法快速求解。另外，本文方法是将结构的设计荷载简化为约束条件，通过与结构原始数据（表3）的对比可知：输电塔结构优化过程是在满足约束条件下进行的，且截面优化、拓扑优化、形状优化和布局优化结果均优于原始模型，均在满足工程设计要求的基础上，实现了结构的质量更轻，造价更低。然而，受制于塔形和结构局部优化的限制，当优化的迭代次数一样时，复杂层次的优化效果并不明显。文献[14]的计算结果表明：对于输电塔结构的局部优化，迭代次数有限时，表5输电塔局部拓扑优化设计结果

Tab.5Local Topology Optimal Design Results of Transmission Tower优化变量优化变量分类造价/元截面1类（Q345L140×10），2类（Q235L80×5），3类（Q235L45×3），4类（Q235L40×3），5类（Q235L40×3），

6类（Q235L70×4），7类（Q235L40×3），8类（Q235L40×3），9类（Q235L40×3），10类（Q345L125×10），

11类（Q235L70×4），12类（Q235L40×3），13类（Q235L40×3），14类（Q235L40×3），15类（Q235L70×4），

16类（Q235L40×3），17类（Q235L45×6），18类（Q235L45×3），19类（Q345L110×10），20类（Q235L80×6），

21类（Q235L45×3），22类（Q235L40×3），23类（Q235L40×3），24类（Q235L70×5），25类（Q235L40×3），

26类（Q235L40×3），27类（Q235L40×3）拓扑拓扑1（类型A），拓扑2（类型A），拓扑3（类型A），拓扑4（类型A），拓扑5（类型A），拓扑6（类型A），

拓扑7（类型A），拓扑8（类型A）87 464表6输电塔局部形状优化设计结果

Tab.6Local Shape Optimal Design Results of Transmission Tower优化变量优化变量分类造价/元截面1类（345L140×10），2类（235L70×5），3类（235L40×3），4类（235L40×3），5类（235L40×3），

6类（235L70×5），7类（235L45×6），8类（235L40×3），9类（235L45×5），10类（345L125×10），

11类（235L70×5），12类（235L40×3），13类（235L40×3），14类（235L40×3），15类（235L75×5），

16类（235L45×3），17类（235L40×3），18类（235L40×3），19类（345L125×8），20类（235L70×7），

21类（235L40×5），22类（235L45×4），23类（235L40×3），24类（235L75×5），25类（235L45×5），

26类（235L45×4），27类（235L40×3）形状X1=1.712 m，Y1=1.712 m，Z1=35.280 m，X2=1.610 m，Y2=1.610 m，Z2=37.900 m87 739图8形状优化设计历程

Fig.8Shape Optimization Design History截面优化变量较少却能表现出较好的优化幅度。因此，虽然本文方法已经可以实现采用一致性的方法求解不同类型的优化问题，但是仍有待改进和完善，并且需要更好地推广到整塔的优化设计中。3结语

（1）本文方法不仅可以同时适用于不同求解难度的输电塔结构局部优化问题，而且无须针对不同问题进行修改。

（2）对比原始模型，截面优化、拓扑优化、形状优化和布局优化结果均优于原始模型。

（3）本文基于离散系统求解结构优化问题的思想更加贴近于实际工程，并且方法易于实现程序化，便于设计者掌握和使用。

（4）本文提出的基于蚁群算法的输电塔结构离散变量优化设计方法具有非常好的发展前景和实用价值。表7输电塔局部布局优化设计结果

Tab.7Local Layout Optimal Design Results of Transmission Tower优化变量优化变量分类造价/元截面1类（345L110×14），2类（235L70×5），3类（235L40×3），4类（235L40×3），5类（235L40×3），

6类（235L70×4），7类（235L45×5），8类（235L40×3），9类（235L40×4），10类（345L140×10），

11类（235L70×5），12类（235L40×3），13类（235L40×3），14类（235L45×3），15类（235L70×5），

16类（235L40×4），17类（235L40×3），18类（235L40×4），19类（345L125×8），20类（235L75×6），

21类（235L40×3），22类（235L45×6），23类（235L40×3），24类（235L70×5），25类（235L40×4），

26类（235L40×3），27类（235L40×3）拓扑拓扑1（类型A），拓扑2（类型A），拓扑3（类型A），拓扑4（类型A），拓扑5（类型A），拓扑6（类型A），

拓扑7（类型A），拓扑8（类型A）形状X1=1.706 m，Y1=1.706 m，Z1=35.440 m，X2=1.610 m，Y2=1.610 m，Z2=37.900 m87 709图9布局优化设计历程

Fig.9Layout Optimization Design History参考文献：

References：[1]SHEPPARD D J，PALMER A C.Optimal Design of Transmission Towers by Dynamic Programming[J].Computers and Structures，1972，2（4）：455468.

[2]GHANNOUM E，YAACOUB S J.Optimization of Transmission Towers and Foundations Based on Their Minimum Cost[J].Power Delivery，1989，4（1）：614620.

[3]RAJEEV S，KRISHNAMOORTHY C S.Discrete Optimization of Structures Using Genetic Algorithms[J].Journal of Structural Engineering，1992，118（5）：12331250.

[4]RAJEEV S，KRISHNAMOORTHY C S.Genetic Algorithmsbased Methodologies for Design Optimization of Trusses[J].Journal of Structural Engineering，1998，124（8）：979980.

[5]王藏柱，董桂西.架空输电铁塔形状优化的研究[J].华北电力大学学报：自然科学版，2001，28（2）：100104.

WANG Cangzhu，DONG Guixi.Investigation on Shape Optimization of Transmission Tower[J].Journal of North China Electric Power University：Natural Science Edition，2001，28（2）：100104.

[6]崔磊，邓洪洲.基于递归思想的输电塔主材统材划分优化方法[J].武汉理工大学学报，2010，32（11）：130134.

CUI Lei，DENG Hongzhou.Optimization Method for Unifying Section of Transmission Towers Chord Member by Recursion[J].Journal of Wuhan University of Technology，2010，32（11）：130134.

[7]邓洪洲，崔磊.输电塔塔身交叉斜材拓扑优化方法研究[J].同济大学学报：自然科学版，2010，38（2）：205213.

DENG Hongzhou，CUI Lei.Synthesis Method for Topology Optimization of Intersecting Bracing Members on Body of Transmission Tower[J].Journal of Tongji University：Natural Science，2010，38（2）：205213.

[8]李林，宋梦娇，王达达，等.输电塔架设计中的离散优化方法研究[J].华北电力大学学报：自然科学版，2012，39（6）：3539.

LI Lin，SONG Mengjiao，WANG Dada，et al.Study of Discrete Optimum Method in Transmission Tower Design[J].Journal of North China Electric Power University：Natural Science Edition，2012，39（6）：3539.

[9]钱令希.工程结构优化设计[M].北京：水利电力出版社，1983.

QIAN Lingxi.Optimum Design of Engineering Structures[M].Beijing：Water Power Press，1983.

[10]孙焕纯，柴山，王跃方.离散变量结构优化设计[M].大连：大连理工大学出版社，2002.

SUN Huanchun，CHAI Shan，WANG Yuefang.Discrete Optimum Design of Structures[M].Dalian：Dalian University of Technology Press，2002.

[11]DORIGO M，MANIEZZO V，COLORNI A.The Ant System：An Autocatalytic Optimizing Process[R].Milano：Politecnico di Milano，1991.

[12] DORIGO M，MANIEZZO V，COLORNI A.Ant System：Optimization by a Colony of Cooperating Agents[J].Systems，Man，and Cybernetics，Part B：Cybernetics，1996，26（1）：2941.

[13]段海滨.蚁群算法原理及其应用[M].北京：科学出版社，2005.

DUAN Haibin.Ant Colony Algorithms：Theory and Application[M].Beijing：Science Press，2005.

[14]张卓群，李宏男.基于蚁群算法的桁架结构布局离散变量优化方法[J].计算力学学报，2013，30（3）：336342.

ZHANG Zhuoqun，LI Hongnan.The Method of Truss Structure Layout Discrete Variable Optimization Based on Ant Colony Optimization[J].Chinese Journal of Computational Mechanics，2013，30（3）：336342.

[15]CAMP C V，BICHON B J.Design of Space Trusses Using Ant Colony Optimization[J].Journal of Structural Engineering，2004，130（5）：741751.

[16]林友新，张卓群，李宏男，等.输电塔结构的拓扑优化设计方法[J].沈阳建筑大学学报：自然科学版，2013，29（4）：655661.

LIN Youxin，ZHANG Zhuoqun，LI Hongnan，et al.Topology Optimization Design of Transmission Tower Structure[J].Journal of Shenyang Jianzhu University：Natural Science，2013，29（4）：655661.