全球气候模式中气候变化预测预估的不确定性*
2016-03-06段青云夏军缪驰远孙巧红
段青云,夏军,缪驰远,孙巧红
①北京师范大学全球变化与地球系统科学研究院,北京 100875;②武汉大学水资源与水电工程科学国家重点实验室,武汉 430072
全球气候模式中气候变化预测预估的不确定性*
段青云①†,夏军②††,缪驰远①,孙巧红①
①北京师范大学全球变化与地球系统科学研究院,北京 100875;②武汉大学水资源与水电工程科学国家重点实验室,武汉 430072
人类活动造成的以全球变暖为主要特征的气候变化对生态系统和人类社会造成严重的影响。全球气候模式正日益成为研究当前气候特征和现象、了解过去气候演变规律及预估未来气侯变化不可替代的、最具潜力的工具。气候模式已被广泛运用于全球和区域未来气候变化的研究中。未来情景的不确定性、气候系统内部的自然变率的不确定性和表征气候过程的不确定性是造成气候预测预估不确定性的主要来源,而概率分布是一个很好地表示气候变化预测不确定性的方式。介绍了贝叶斯多模式推断方法来描述气候变化预估不确定性的理论框架,并以中国区域为例,利用IPCC-AR5的气候模式数据,通过贝叶斯多模式推理方法预估未来中国区域的南北方两个典型流域(海河和珠江流域)未来气候变化情况。结果表明:中国区域都将呈现出变暖的趋势,在RCP2.6、RCP4.5和RCP8.5情景下,温度变化趋势分别为0.91±0.30°C/100a、2.41±0.77°C/100a、6.08±1.01°C/100a;降水也呈现出增加的趋势,三种情景下的趋势分别为(5.58±2.96)%/100a、(10.30±4.30)%/100a和(15.90±6.68)%/100a;中国海河流域的年降水量在2020s和2040s都将出现增加的趋势,珠江流域则在2020s略有降低,2040s开始增加。并且在2020s和2040s发生干旱和极端暴雨等极端降水事件的概率同时增加。
气候变化预估;全球气候模式;不确定性量化;贝叶斯多模型推理方法
气候变化是指特定地区的气候平均状态随时间的变化(一般为年代际尺度),这与天气的短时变化(几分钟到几天)是不一样的[1]。气候变化可能由多种因素造成,包括太阳黑子等太阳活动引起的地表吸收的净辐射变化、地球轨道的变化、板块运动或大规模的火山活动,以及大气和海洋环流变化等自然因素。人类活动,特别是工业革命以来的人类活动,包括化石燃料燃烧和其他工业活动所造成的二氧化碳等温室气体的排放、土地利用变化、大规模城市化等,也会引起气候的变化。温室气体能够吸收地球表面的辐射能量,阻止红外辐射直接进入太空,由此造成的“自然温室效应”会使地球温度升高[2-3]。许多研究表明气候变化也称全球变暖。以全球变暖为主要特征的气候变化不仅对人类生存环境造成严重的影响,并可能进一步导致水资源、生态系统状况发生变化,造成旱涝等自然灾害的频发,对工农业生产,社会经济发展、人类健康和政治格局等产生深远的影响[4]。气候变化及其影响已成为当前全球性的重大科学问题,并受到各国政府和公众的关注[5]。
目前,科学界主要通过观测和气候模式模拟对过去和未来的气候变化进行分析和理解。观测和气候模式模拟是了解和研究过去气候变化的重要手段。政府间气候变化委员会第五次气候报告(IPCC-AR5)指出,1880—2012年,全球海陆表面平均温度呈线性上升趋势,共升高了0.85 °C;最近30年(1983—2012)可能为自1400年来最热的30年[5]。气候模式是作为气候变化归因与预测未来气候变化的唯一工具。根据世界上各气候变化研究机构开发的最先进的全球气候模式(GCMs)的模拟结果,预测到21世纪末全球平均地表温度可能升高0.3~4.8 °C[5]。
1 气候变化预估的不确定性
气候预测的不确定性主要有三个来源:①情景的不确定性,即未来温室气体排放的不确定性;②气候系统内部的自然变率的不确定性;③表征气候过程的不确定性,即气候模式的结构框架不确定性[6]。
温室气体排放水平的不确定性是造成未来气候预测不确定性的重要来源,它是与未来技术发展和社会经济政策的不确定性是相关联的。在IPCC-AR5中采用了典型浓度路径(representative concentration pathways,RCPs)来描述在2006—2100时期随时间和空间变化的全球温室气体浓度。根据这些温室气体浓度在2100年相当的辐射强迫增幅的数值大小分成了四种RCP情景:RCP2.6,RCP4.5,RCP6.0和 RCP8.5,分别表示2100年辐射强迫相对于工业革命前的增幅分别为2.6 W/m2,4.5 W/m2,6.0 W/m2和8.5 W/m2。每种RCPs都有其相应的社会经济假设[7],其中RCP2.6定义辐射强迫峰值出现在2010—2020年,并在之后开始出现下降。RCP4.5的排放是在2040年左右达到峰值而后下降。RCP6.0在2080左右为峰值。在RCP8.5中,排放总量持续增长到21世纪末。根据IPCC-AR5报告,到2100年全球平均地表温度在RCP2.6,RCP4.5,RCP6.0和RCP8.5情景下的预计增温分别为1.0 °C,1.8 °C,2.2 °C和3.7 °C[8]。
由于气候系统内部的自然变率造成的气候变化预测的不确定性主要来源于太阳辐射、太阳活动、潮汐运动等;同时大气圈、水圈、冰雪圈、岩石圈和生物圈的相互作用也会造成气候系统内部的变化。气候系统各个组成部分之间在不同的时空尺度上存在着复杂的非线性相互作用关系,从而导致气候过程具有极大的复杂性,使气候变化难以预测。如何准确地表征气候系统及过程依然是一个难题,现有手段还存在着较大的局限性。虽然现在有许多不同的全球气候模式,但它们也只是通过简化真实世界的气候过程来表征和模拟气候变化,这也就带来气候变化预估较大的误差和不确定性。由于气候模式的不确定性,IPCC-AR5中不同气候模式在RCP2.6,RCP4.5,RCP6.0和RCP8.5情景下的预计地表温度在2081—2100年增温的可能区间分别为1.3~0.7 °C,1.1~2.6 °C,1.4~3.1 °C和2.6~4.8 °C。
气候模式模拟存在着不确定性,必然带来这样的问题:如何量化气候变化预测的不确定性?一种常用方法是通过度量不同模式预测值的范围来定量描述。这个方法的主要缺点是它是建立在所有的模型模拟效果相同的假设上。实际上,不同模式的模拟性能存在差异,这些差异来自模式的结构框架、模式对物理的描述和模式中各物理参数的选取,有些全球气候模式模拟性能会优于其他模式。因此有的研究者提出在预估未来气候变化中性能好的模式应该给予更大的权重系数[9],而这也就提出了一个关于评估GCM预测是否“正确”的命题。往往我们用“似然值”来表征一个命题是否正确的可能性,似然值是来自于概率和统计理论的术语,它是描述一个假设是否成立的概率值。相对于用模式之间预估值的范围来表征不确定性,概率分布是一个更好的方式,现有的气候变化研究机构越来越多地采用它来描述长期气候变化预测的不确定性。
用概率分布来描述不确定性的一个优势是能够提供更多预报信息,概率分布不仅提供了最可能发生的结果,还能提供特定事件发生的可能性,包括极端事件的发生概率。理解气候变化实际上要关注相关气象变量概率分布的变化。图1(a)显示了一个假想地表气温的概率分布变化,其中温度概率分布以高斯分布来表示。图中竖线分别表示均值,阴影区域表示极端事件出现的概率(红和蓝色区域分别表示极端高温和极端低温出现概率)。图1(b)显示出在气候变化背景下,地表温度的概率分布向右偏移,并伴随均值和方差的变化。从图中可以看出,相比较现在气候,不确定性区间在扩大,未来气候的温度均值在上升,极端高温出现的概率(红色阴影的面积增加)在大幅增长,而极端低温出现的概率(蓝色阴影面积)基本不变,但是极冷温度范围往左延伸,意味着比过去更冷的温度可能出现。
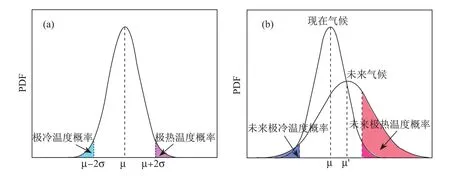
图1 地表温度的概率分布变化示意图(PDF:概率密度函数)
2 量化气候变化预估不确定性的贝叶斯方法
根据以上描述,我们知道概率分布是一个很好地表示气候变化预测不确定性的方式。然而如何构建概率分布呢?贝叶斯推理给我们提供了很好的工具,它能够依据证据(观测)推断一个随机变量的后验概率分布。这一推理过程是基于贝叶斯理论,它规定给定一个假设,该假设基于观测而得到的后验(新)分布是与它的先验分布与该假设的似然值的乘积成正比。在气候模式中,学者经常利用过去气候观测数据来估算气候模式是否“正确”这一假设的似然值。关于贝叶斯方法的具体介绍在相关的贝叶斯理论书籍中都可以看到。文章中我们介绍了基于贝叶斯推理的贝叶斯多模式推理方法。
在贝叶斯多模式推理方法中,定义随机变量y为预测向量值,D为相应的观测值,M={M1, M2,…,MK}是采用的全部模型的模拟数据集。假设这些模型预测来自y的某种概率分布的随机量。y的后验分布可以写成
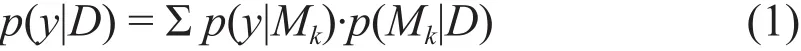
其中,p(y|Mk) 是模型k对于y的后验分布(即模型k对y的概率预测),p(Mk|D)是模型k正确预测出D的似然值。给定观测,y的后验分布就是通过每一个单个模型后验分布y的加权平均值,权重等于第k个模式预测正确的似然值,p(Mk|D) 。我们把p(Mk|D) 定义为权重wk,并假定p(y|Mk)由某些参数概率分布函数f(y|θk,Mk)表示,那么方程(1)可以表示成
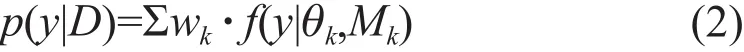
其中,wk和 θk,k=1,…,K,是未知参数,K是模型数量。一般来说,似然方程比概率密度函数更容易用来估计wk和θk。假定y是高斯分布(即f(y|θk,Mk)=g(y|θk,Mk)),那么似然方程可以表述为
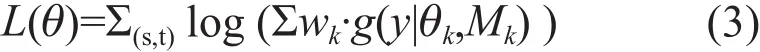
这里(s,t)表示y的空间与时间指标。wk和θk可以通过最大似然方法来估计,例如期望最大化算法(Expectation-Maximization,EM)可来解出wk和θk,但是如果y的概率分布不满足高斯分布假设,我们可以通过其他手段来估计wk和θk的极大似然值,如遗传算法或蒙特卡罗马尔可夫(MCMC)算法等。
Duan和Phillips[10]提出了贝叶斯多模式推理方法去评估气候变化预测的不确定性。对于变量y,y={y(p),y(f)},y(p)和y(f)分别表示感兴趣的变量在现在气候和未来气候中的量。假定y(p)和y(f)是独立的,在方程(3)中的g(y|θk,Mk)可以表示为
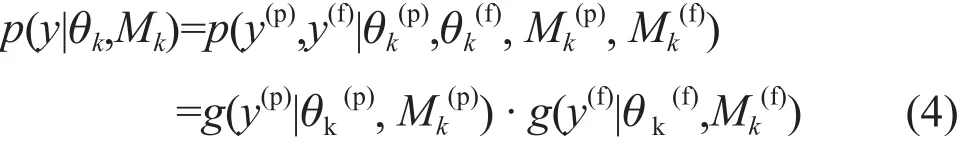
将方程(4)代入方程(3),wk和θk可以通过EM算法估计。因为我们假设地表温度为高斯分布,那么可以得到θk(p)=(µk(p),σk(p)) 和θk(f)=(µk(f),σk(f)),µk(p)和µk(f),σk(p)和σk(f)分别是g(y|θk(p),Mk,σk(p)) 和g(y|θk(f),Mk,σk(f))的均值和标准差。对于每个模式,这里假定µk(p)=Mk(p),µk(f)=Mk(f)。那么剩余的未知参数是wk,σk(p)和σk(f),k=1,2,…,K。EM算法是一个迭代过程,在E(期望)步与M(最大化)步之间迭代。为实现EM算法,需要引入一个非观测变量zkst。对每个集合成员的σk(p,0),σk(f,0)和wk(0)初始化后,zkst,σk(p), σk(f)和wk通过以下的方式开始不断迭代计算:
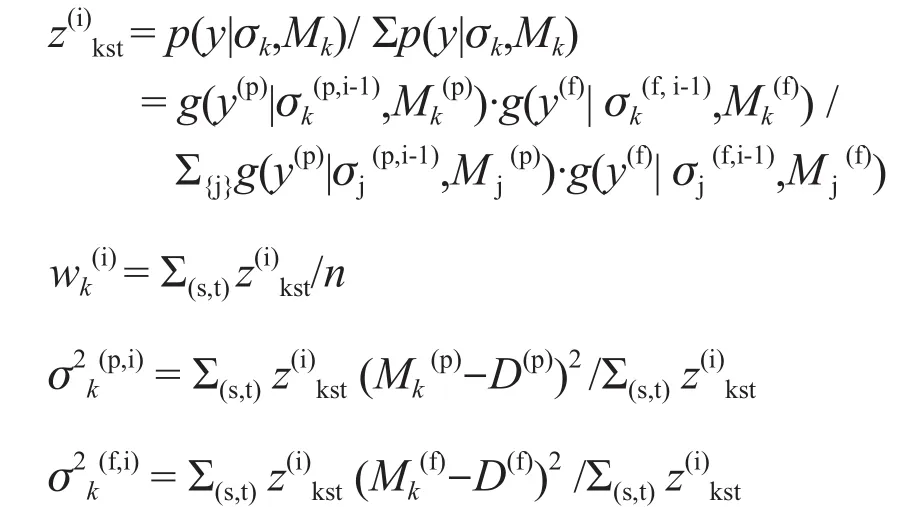
其中,n是空间和时间上的所有数据点数。z(i)kst,σk(p,i),σk(f,i)和 wk(i)在上述过程中不断反复迭代计算,直到收敛为稳定的值。最终得出的值用于计算多模式概率预测。y的多模式期望值为单个模式预测的加权平均,多模型估计的总方差是模式间的方差和模式内方差之和。
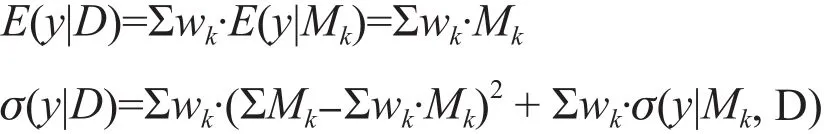
Duan和Phillips[10]利用贝叶斯多模式推理方法基于IPCC-AR4[11]中多个模式来预测全球地表气温和降水到21世纪末的变化。在下一节中,我们将演示如何利用贝叶斯多模型框架来评估IPCC-AR5 GCM的模式在中国整个大陆和两个典型流域(海河流域和珠江流域)的气候变化预估。
3 利用贝叶斯多模式推理方法预估中国气候变化
与全球其他地方一样,中国不可避免地受到气候变化的影响,给国家的环境、生态系统、农业和经济造成严重的影响。根据第三次气候变化国家评估报告[12],1909—2011年,中国陆地表面平均温度上升了0.9~1.5 °C,最近15年为历史有记录以来的最热阶段。虽然在这个阶段全国的年降水量没有显著的变化,但在区域尺度上,年降水量发生了显著变化,在过去30年,西部干旱和半干旱区的降水增加。气候变化也给中国的水环境带来了灾难性的影响。中国海岸带的海平面在1980—2012年期间以2.9 mm/a的速率上升。从1970年到21世纪初,中国冰川已经减少10.1%,冻土减少18.6%。第三次气候变化国家评估报告也对中国未来的气候变化进行了预测。报告指出中国地表气温在21世纪将持续增加,增温范围为1.5~5.0 °C。全国降水在21世纪可能增加2%~5%,到21世纪末海平面可能上升0.4~0.6 m。气候变化将会带来更为频繁的干旱,极端暴雨和其他气象灾害事件。下面,我们将展示通过贝叶斯多模式推理方法得出的中国未来气候变化的结果。我们将基于IPCC-AR5的全球气候模式的模拟结果,预测未来中国的气候变化情况,并给出不确定性信息,在以下的结果中我们考虑了三种排放情景:RCP2.6,RCP4.5和RCP8.5,RCP6.0的情景没有考虑,但是该情景应该处于RCP4.5和RCP8.5之间。
图2利用贝叶斯多模式推理方法预估2006—2099年中国区域气温和降水的变化情况。可以看出,在RCP2.6,RCP4.5和RCP8.5三种未来情景下,中国区域都将呈现出变暖的趋势,从2006—2099年的变化趋势分别为0.91±0.30 °C/100a,2.41±0.77 °C/100a,6.08±1.01 °C/100a。中国区域的降水也呈现出增加的趋势,在RCP2.6,RCP4.5和RCP8.5情景下的趋势分别为(5.58± 2.96)%/100a,(10.30±4.30)%/100a和(15.90± 6.68)%/100a。图2(a)中的结果与第三次国家气候变化评估报告的结论相似,但是RCP8.5情景下给出的最高温度在6.0 °C以上,高于第三次国家气候变化评估报告的5.5 °C。
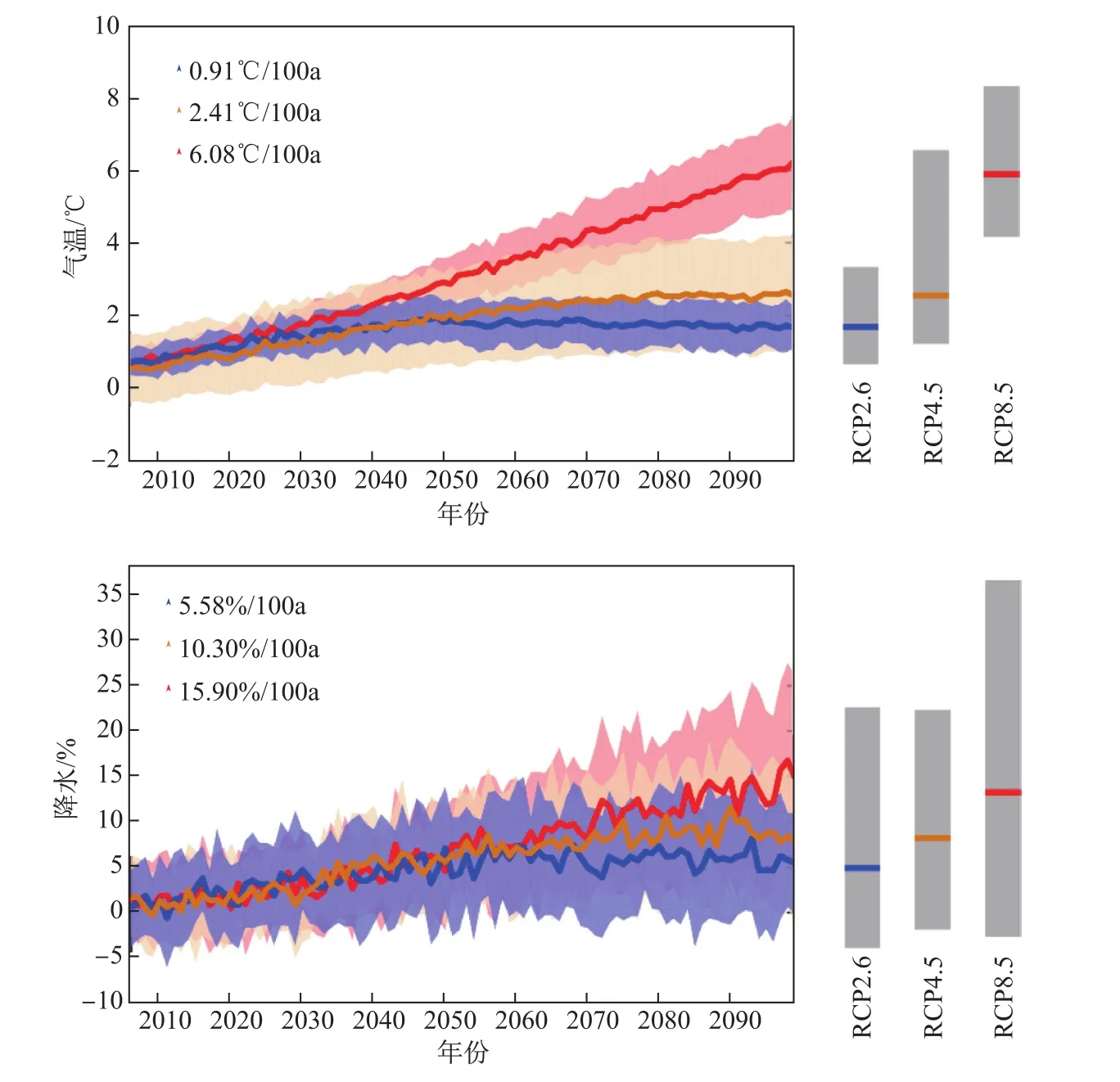
图2 多模式结果对中国区域温度与降水的模拟与不确定性区间。蓝色、橙色、红色的实线表示温度和降水在2006—2099年RCP2.6、RCP4.5和RCP8.5情景下时间序列变化,蓝色、橙色、红色的阴影表示用BMA算出的均值加减一个方差的范围。图中右边灰色阴影表示GCMs模型在2090—2099年预测的气候变化范围,灰色阴影中的实线表示用BMA方法得到的2090—2099年在三种情景下温度和降水变化的最佳估值
图2给出了不同气候变化情景下的地表温度和降水的预估范围。下面我们利用贝叶斯多模型推理方法来求这些变量的概率密度函数(PDF),用其来表征不同流域未来的温度和降水预估的不确定性(图3和图4)。研究选取了整个中国大陆、北方(海河流域)和南方(珠江流域)两个典型流域作为对比,我们选取了21世纪两个比较接近现在的年代:2020s和2040s。研究结果表明,中国大陆、海河和珠江流域,温度都呈现逐年代增加的趋势,相比1990s,在RCP2.6、RCP4.5和RCP8.5情景下,2020s和2040s的温度均值和方差都有显著增加。在2020s,三种情景温度变化的区别并不是很大,而在2040s,温度增温的大小显示出RCP2.6<RCP4.5<RCP8.5趋势。这主要与RCPs情景温室气体溶度设定的变化过程有关,以RCP8.5的结果最为严峻。值得注意的是,在所有的情景下,未来气候下的地表温度均值已经超过1990s地表温度的可变化范围。随着PDF的向右移动,在未来气候下,这意味着今后极端高温事件发生的概率会大大增加(图3)。对于降水的预估(图4),相比1990s,中国大陆和海河流域的年降水量在2020s和2040s都表现出增加的趋势,PDF整体相右移动,而珠江流域则在2020s却略有降低,特别是在RCP4.5和RCP8.5情景下。降水在2040s整个中国大陆和两个典型流域都全面增加。从图中PDF的分布情况看,在未来2020s和2040s年代极端降水相对于1990s都显现出一定的增加趋势。虽然2020s的降水均值变化较少或略有下降,但是发生极端降水发生干旱和极端暴雨的概率可能同时增加,这就意味着今后中国的年降水量可能增加,我们也将面临更多的干旱和洪水灾害。
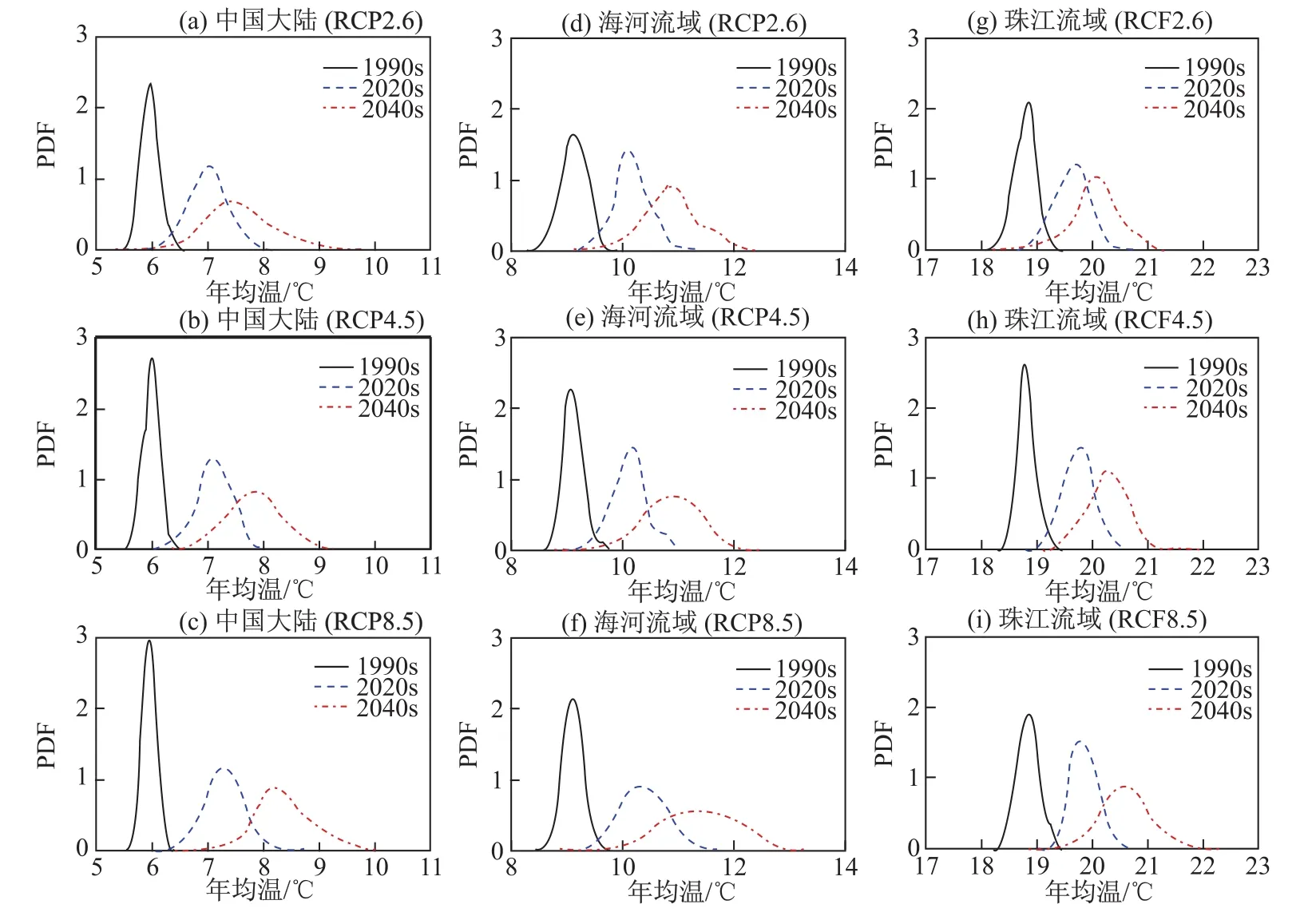
图3 中国大陆和典型流域年均温在不同年代的变化
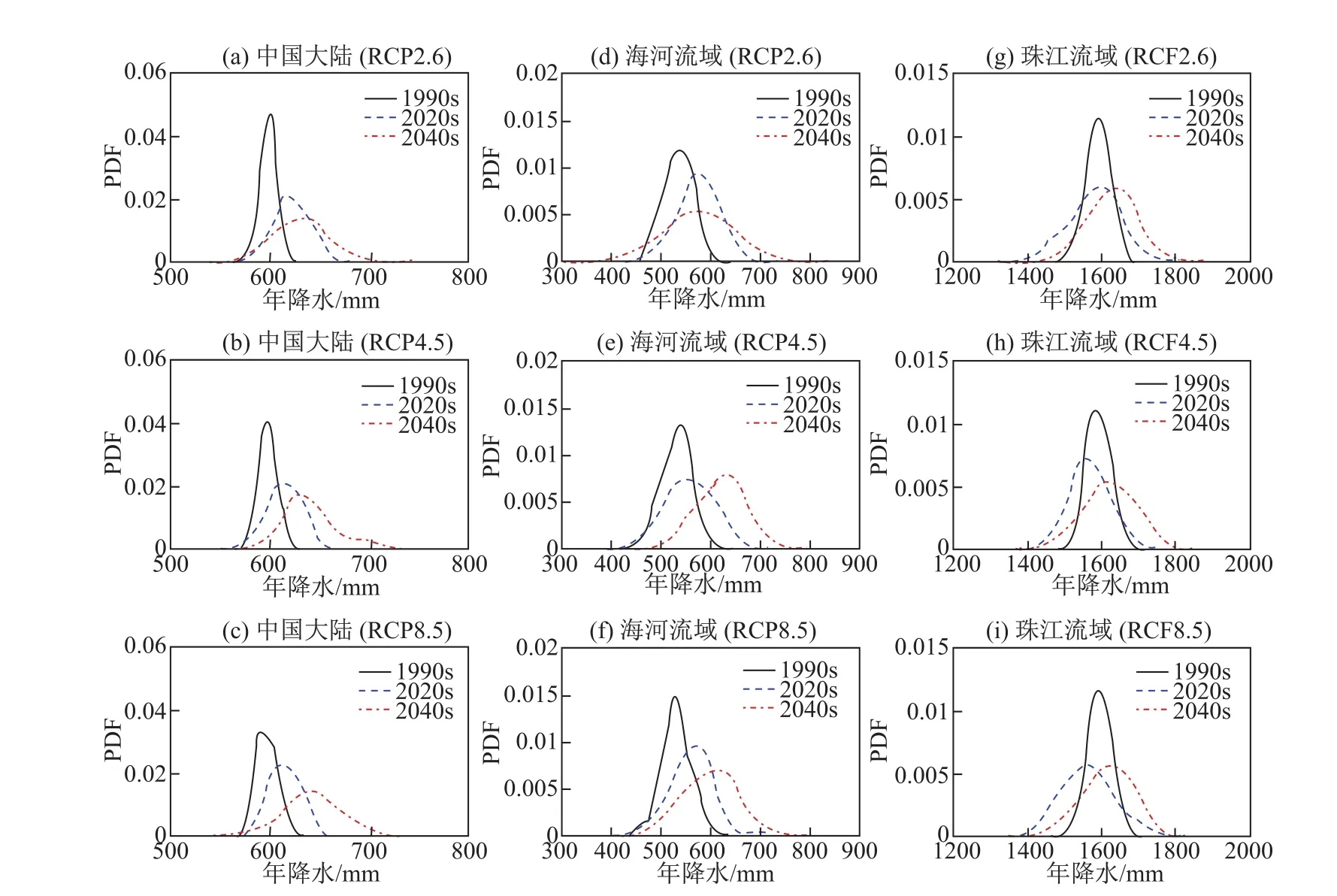
图4 中国大陆和典型流域年降水量在不同年代的变化
4 结论
气候变化是我们人类面临的一个极大挑战。由于气候系统受复杂的自然变化因素和我们认知限制的影响,气候变化预估还存在很大的不确定性。随着我们的科学技术的发展,我们量化自然的不确定性和降低认知上的不确定性的能力大大提高,从而提高气候变化预估的可靠性。本文中的贝叶斯多模型推理方法能够帮助获取未来气候变化预估的概率分布,这些信息结合风险决策理论,能够为制定减缓和适应气候变化的政策提供科学支撑。
(2016年5月4日收稿)
[1] 丁一汇. 气候变化的事实和科学认识[J].气象知识, 2004, 1:8-12.
[2] 周天军, 陈晓龙.气候敏感度, 气候反馈过程与 2℃ 升温阈值的不确定性问题[J].气象学报, 2015, 4: 2. doi: 10.11676/qxxb2015.057.
[3] 秦大河, 陈振林, 罗勇, 等. 气候变化科学的最新认知[J].气候变化研究进展, 2007, 3(2): 63-73. doi: 1673-1719 (2007) 02-0063-11.
[4] 夏军, 刘春蓁, 任国玉. 气候变化对我国水资源影响研究面临的机遇与挑战[J]. 地球科学进展, 2011, 26(1):1-12. doi: 1001-8166(2011)01-0001-12.
[5] IPCC. Climate change 2014: impacts, adaptation, and vulnerability. Part A: global and sectoral aspects. Contribution of working group II to the fi fth assessment report of the intergovernmental panel on climate change [M]. Cambridge: Cambridge University Press, 2014: 1132.
[6] HAWKINS E, SUTTON R. The Potential to narrow uncertainty in regional climate predictions [J]. Bulletin of the American Meteorological Society, 2009, 90: 1095-1107.
[7] MOSS R, BABIKER M, BRINKMAN S, et al. Towards new scenarios for analysis of emissions, climate change, impacts, and response strategies [C]. Geneva: Intergovernmental Panel on Climate Change. 2008: 132.
[8] IPCC. Climate change 2014: synthesis report. Contribution of working groups I, II and III to the fifth assessment report of the intergovernmental panel on climate change [M]. Cambridge: Cambridge University Press, 2014: 151.
[9] SANTER B D, TAYLOR K E, GLECKLER P J, et al. Incorporating model quality information in climate change detection and attribution studies [J]. Proc Natl Acad Sci, 2009, 106(35): 14778-14783.
[10] DUAN Q, PHILLIPS T J. Bayesian estimation of local signal and noise in multimodel simulations of climate change [J]. J Geophys Res, 2010, 115: D18123. doi:10.1029/2009JD013654.
[11] IPCC. Climate change (2007), The physical science basis, working group 1 contribution to the fourth assessment report of the intergovernmental panel on climate change [M]. Cambridge: Cambridge University Press, 2007: 996.
[12] 气候变化国家评估报告编写委员会. 第三次气候变化国家评估报告[M]. 北京: 科学出版社, 2015: 710.
(编辑:温文)
The uncertainty in climate change projections by global climate models
DUAN Qingyun①, XIA Jun②, MIAO Chiyuan①, SUN Qiaohong①
①College of Global Change and Earth System Science, Beijing Normal University, Beijing 100875, China; ②State Key Laboratory of Water Resources & Hydropower Engineering Science, Wuhan University, Wuhan 430072, China
Global warming caused by human activities has devastating impacts on the Earth’s eco-system and the human society. Climate models are the primary tools available for investigating the response of the climate system to various forcings and for making climate change projections into the future. Climate change projections are plagued by various sources of uncertainties, including the greenhouse gases emission scenarios, the internal variability of the climate system, and the representation of the climate processes. To cope with future climate changes, one must quantify those uncertainties properly. Probability distribution is an excellent way to describe the uncertainties. We presented the Bayesian multi-model inference methodology to quantify uncertainty in the climate change projections. We applied this Bayesian framework to assess the climate change projections contained in IPCC-AR5 in the continental China and in two typical large basins in China (Haihe and Pearl River). The results showed that warming is expected all over China under all emissions scenarios. The warming trend from 2006 to 2099 in China is 0.91±0.30 °C/100a, 2.41±0.77 °C/100a, and 6.08±1.01 °C/100a under RCP2.6, RCP4.5 and RCP8.5 scenarios, respectively. Precipitation in China is also projected to be increasing during the 21st century by (5.58±2.96)%/100a, (10.30±4.30)%/100a, and (15.90±6.68)%/100a for the three RCP scenarios, respectively. Under climate change, extreme temperature and precipitation events are projected to be more probable in the future with the probability distribution shifting to the right for both temperature and precipitation.
climate change projection, global climate model, uncertainty quanti fi cation, Bayesian multi-model inference method
10.3969/j.issn.0253-9608.2016.03.004
*国家重点基础研究发展计划(973计划)(2010CB428400)和国家自然科学基金面上项目(41375139)资助
†通信作者,E-mail: qyduan@bnu.edu.cn
††中国科学院院士,研究方向:系统水文学非线性理论与方法、生态水文与水资源可持续管理。
