基于核密度估计方法的涤棉混纺纱拉伸断裂声发射信号分析
2016-03-03林兰天辛斌杰申炎仃
王 瑾,林兰天,高 琮,辛斌杰,申炎仃
(上海工程技术大学服装学院,上海 201620)
基于核密度估计方法的涤棉混纺纱拉伸断裂声发射信号分析
王瑾,林兰天,高琮,辛斌杰,申炎仃
(上海工程技术大学服装学院,上海201620)
摘要:为了研究涤棉混纺纱拉伸断裂过程中各组分纤维的断裂情况,自主搭建了声发射信号采集装置,分别采集纯涤纶、纯棉和涤棉混纺环锭纱的拉伸断裂声发射信号,采用HHT和ICA分析方法将声发射信号的时域信号转换成频域信号,并提取特征量频率与幅值。基于核密度估计方法对涤棉混纺纱的拉伸过程中涤纶与棉纤维的声发射信号进行分析。结果表明:涤棉混纺纱拉伸过程中其组分纤维的声发射信号可以用特征频谱表征;在拉伸过程的每一个阶段,各种材料声发射特征频谱的不同可以由特征频率的核密度估计表达,并可推测其组分纤维的断裂次序。
关键词:纤维制造技术;涤棉混纺纱; 核密度估计; 特征频谱; 声发射; HHT; ICA; 拉伸断裂
王瑾, 林兰天, 高琮,等.基于核密度估计方法的涤棉混纺纱拉伸断裂声发射信号分析 [J].河北科技大学学报,2016,37(1):83-87.
WANG Jin, LIN Lantian, GAO Cong,et al.Analysis of acoustic emission signal of polyester/cotton yarns in the moment of tensile fracture by kernel density estimation method[J].Journal of Hebei University of Science and Technology,2016,37(1):83-87.
涤棉混纺纱是最常见的二组分混纺纱,其组分中各种纤维的弹性模量、伸长率以及断裂强度相差很大,对成纱的力学性能尤其是拉伸断裂强度产生一定影响[1]。材料受外力或内力作用产生变形或断裂,应变能以弹性波形式释放会产生声发射现象。不同种类的材料物理化学属性和空间结构各不相同,其声发射信号特征也不相同[2-4]。涤棉混纺纱因其组分纤维种类的不同在拉伸过程中会产生丰富的声发射信号,若单一组分的声发射特征已知,就有可能通过分析声发射信号的特征量获知混合材料的信号归属。
材料拉伸断裂的声发射信号是一种非线性、非平稳的时域信号,常选用短时傅里叶变换(STFT)、小波变换(WT)[5-7]和希尔伯特黄变换(HHT)等时频分析方法将时域信号转换成频域信号进行分析,进而分析信号的每一个频率分量。希尔伯特黄变换(HHT)作为一种新型时频分析方法用于处理非线性非平稳信号具有较高的解析分辨率,在包括纺织材料的材料拉伸断裂研究中的应用在迅速扩大[8-11]。纱线的拉伸信号具有猝发性,内涵丰富,使用以上3种时频分析方法对声发射信号进行时频变换会产生大量的衍生频率,陈群涛[12]、李林洁[13]、贾瑞生等[14]研究将希尔伯特黄变换(HHT)、独立成分分析(ICA)与快速傅里叶分析(FFT)相结合对原始信号进行筛选和剔除实现了特征信号的提取。
核密度估计方法是概率论中用于估计未知数据集的密度函数,是一种非参数估计方法,常用于判别非参数数据集的分布特征,与直方图估计相比密度函数更平滑且不受数据维度的限制[15]。由于多种时频分析方法相结合的技术目前尚不成熟,且纱线因其组分纤维的细度、长度、强度、弹性以及断裂伸长的不同而造成的纤维差异大,断裂特征会有很大不同,因此,所提取的声发射信号特征频率也具有数量大(频率个数可达上千个)、分辨率不高等特点,很难从这些大量特征频率中分析和辨识纱线拉伸断裂的行为。需结合数学方法对混纺纱中不同组分纤维的声发射信号的特征频率进行分类和识别以分析其纱线整体的拉伸断裂机理。本文基于核密度估计的方法,从概率分布密度的角度来判断涤棉混纺纱拉伸断裂声发射信号。
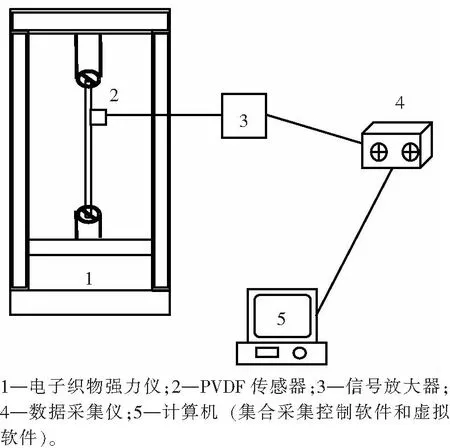
图1 声发射检测系统示意图Fig.1 Diagram of acoustic emission testing system
1试验
1.1 试验材料与设备
3种环锭纱:纯棉纱(21 s)、涤纶纱(20 s)、涤棉混纺纱(21 s T/C40/60);凡士林(耦合剂);YG065C型电子织物强力仪。
声发射检测系统系自主搭建,其示意图如图1所示,主要由声发射传感器、信号放大器、M2i.4911-exp型多通道数据采集卡、数据采集控制软件4个部分组成。
1.2 试验方法
将试样固定在电子织物强力仪的夹具上,将PVDF传感器背面粘贴软磁铁,其接触纱线面涂抹适量凡士林,调整PVDF传感器支架使传感器接触纱线,将薄铁片轻轻地贴附在PVDF传感器正面,使纱线与传感器充分接触。设定电子织物拉伸仪试验参数和数据采集软件参数,进行纱线的定速拉伸试验。
电子织物拉伸仪拉伸速度为250 mm/min,试样拉伸隔距为70 mm,每组试验次数为15次。环境温度t=(25±2)℃,相对湿度RH=65%。试验前已将试样在试验的标准条件下放置24 h,以使试样达到平衡回潮率。
数据采集软件设置采样启动阈值为10 mV,采样频率10 MHz,采样点数2×106。
2对声发射信号的处理
对纯涤纶、纯棉与涤棉混纺环锭纱的拉伸断裂声发射信号进行分解,得到数千个准特征频率,经过筛选、剔除之后形成相互独立的频率集合,其数量近千个,仍无法对单个频率或者某个频率段进行判断或者定义。因此,探讨以声发射信号的特征频率谱来表征纱线拉伸断裂情况。声发射信号的处理过程如下。
1)以Matlab软件为平台编制声发射信号处理程序,分别处理涤纶纱、纯棉纱的拉伸断裂声发射信号(见图2、图3),以图中横坐标上主断裂区中的声发射信号主峰峰值点为中心向左右两边各截取10 000点作为分析区间。从图2、图3的声发射信号图可以看出,拉伸断裂是一个过程,材料的断裂不是瞬间完成的。根据采样频率和采样点数,可知拉伸断裂过程中材料的应力应变能集中释放,持续时间为(2±0.4) ms。
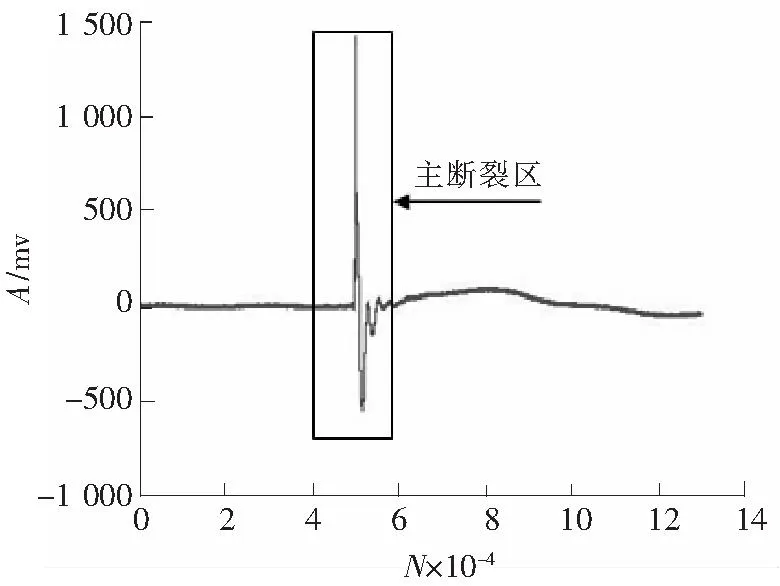
图2 涤纶纱拉伸断裂的原始信号Fig.2 Original signal of polyester yarn in tensile fracture process

图3 纯棉纱拉伸断裂的原始信号Fig.3 Original signal of cotton yarn in tensile fracture process
2)以希尔伯特黄变换(HHT)为基本算法对解析信号作独立成分分析(ICA)[10-11];对各独立成分作快速傅里叶变换(FFT)将时域信号转换成频域信号得到幅值谱,从中筛选出幅值为前5%的峰值点;而后,对比涤纶纱和纯棉纱声发射信号的15个样本,将独有频率以及高频数(相对另一种纤维)作为该种纤维的拉伸断裂声发射特征频率集合。该集合涵盖了被测材料包括纤维间滑移、伸长、断裂在内的全部信息。
3)对涤棉混纺纱拉伸断裂信号进行分段处理,操作方法同上。分段处理方法如下:以声发射信号主峰峰值点为中心前后10 000点为分段,该段即涤棉混纺纱的主断裂区。为了识别特征信号出现的时间位置,观察声发射信号原始图,以主断裂区为基础段,分别向左推移10 000点2次,在主断裂区前截取2段有效信号;而后以主断裂区为基础段向右同样截取7段,加上主断裂区1段,共截取有效信号11段。以涤纶纱和纯棉纱2组纱线的特征信号为依据,在涤棉混纺纱的11个分段中寻找涤纶纱与纯棉纱的特征频率。涤棉混纺纱拉伸断裂声发射信号图如图4所示。
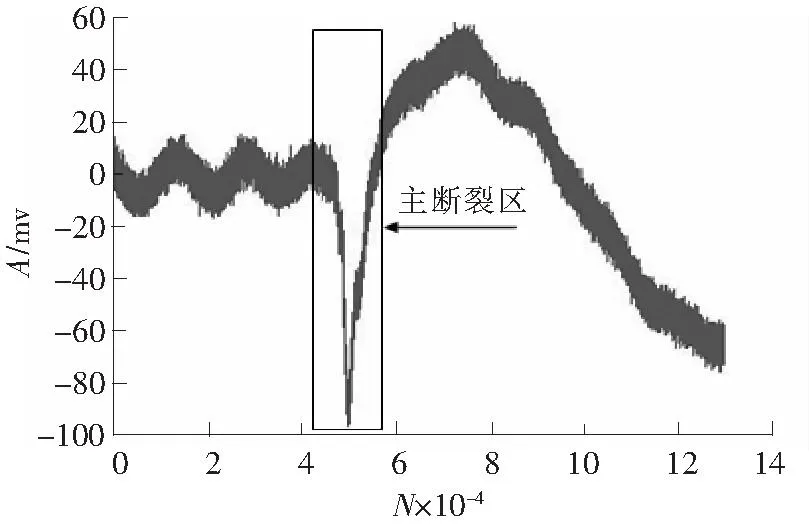
图4 涤棉混纺纱的拉伸断裂原始信号Fig.4 Original signal of the polyester/cotton yarn in tensile fracture process
3基于核密度估计的声发射信号分析
核密度估计具有优良的数据聚类分析特点,能很好地对涤纶纱和纯棉纱的特征频率进行分类分析[15]。为了对涤棉混纺纱拉伸断裂过程中涤纶与棉纤维的断裂的特征频谱进行分析,本文利用Matlab平台自带的ksdensity函数[16]对每一段涤棉混纺纱的信号分解后寻找到的涤纶和纯棉纱的特征频率组合做概率密度分析,计算得每一分段两种单一纤维纱线的特征频率的概率分布,从而获得涤纶和纯棉纱各自拉伸断裂声发射信号特征频率分布概率密度估计,如图5所示。
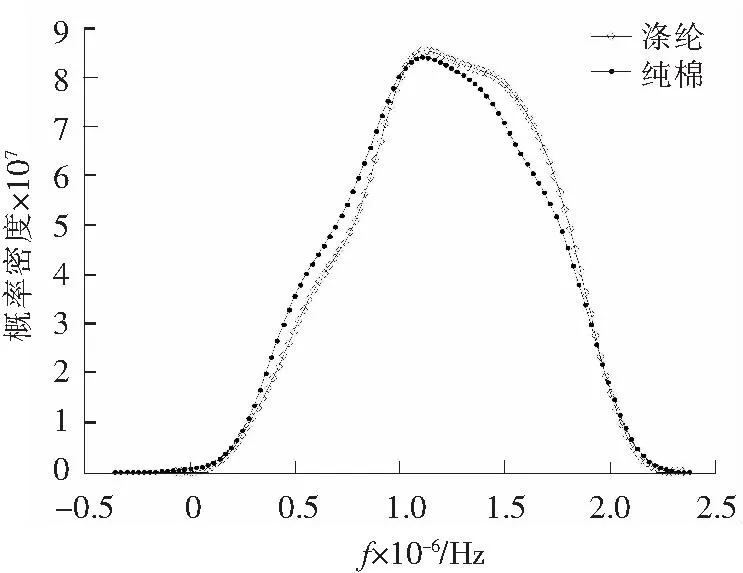
图5 涤纶和纯棉纱拉伸断裂信号特征频率的概率密度估计Fig.5 Probability density of characteristic frequency on acoustic signal of polyester and cotton yarns in tensile failure process
从图5可知,涤纶纱和纯棉纱两者特征频率的概率密度分布曲线具有相似性,但也存在差异:纯棉纱的特征频率在低频部分较密集,涤纶的特征频率在高频部分较密集;二者的概率密度最高的频率主要分布在1×106Hz左右,涤纶断裂的特征频率概率密度最大值为1.124×106Hz,棉纤维断裂的特征频率概率密度最大值为1.104×106Hz。由于信号分析区间选在主断裂区,即断裂能量最为集中释放的区间,因此1.124 MHz可视作为涤纶断裂的特征频率,1.104 MHz可视作为棉纤维断裂的特征频率。
对涤棉混纺纱拉伸断裂声发射信号主断裂区及主断裂区前3段进行与涤纶纱和纯棉纱特征频率相关的核密度估计分析,分别得到主断裂区及主断裂区前3段的涤纶与棉纤维特征频率的概率密度,如图6、图7所示。而涤棉混纺纱拉伸断裂各阶段涤纶与棉特征频率的概率密度分布见图8。

图6 涤棉混纺纱主断裂峰及其前3段涤纶声发射信号的频率概率密度Fig.6 Probability density of characteristic frequency on the main peak and the former three parts of polyester of polyester/cotton yarn in tensile failure process

图7 涤棉混纺纱主断裂区及其前3段棉特征信号的频率概率密度Fig.7 Probability density of characteristic frequency on the main peak and the former three parts of cotton of polyester/cotton yarn in tensile failure process
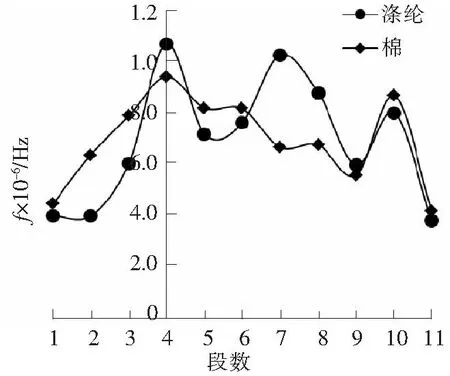
图8 涤棉混纺纱拉伸过程中各阶段最大概率密度点曲线图Fig.8 Curves of the maximum probability densitypoints on polyester/cotton yarn in tensile failure process
图6、图7显示涤纶、棉纱的声发射信号特征频率概率核心密度值在这4段有明显差异。一般而言,纱线拉伸断裂过程包括纤维伸长、断裂和滑移,纤维断裂时内部应变能瞬间释放产生高频信号,纤维间滑移时产生低频信号。图7显示棉纤维在第1段(主断裂区前第3段)的特征频率高密度集中在相对低频段(0.5 MHz左右),而主断裂区概率密度最大的特征频率在1 MHz左右,未靠近主断裂区,可推测主要为棉纤维间的摩擦滑移与纤维伸长,无纤维断裂,这与纱线力学性能基本一致;图7第2段和第3段的特征频率概率密度分布曲线形态极为相似,特征频率带与主断裂区(第4段)重合较多、频率带中心接近(即高概率密度的频率相近),呈现明显的纤维开始断裂迹象。图6第1、第2段的特征频率也高密度集中在相对低频段(0.5 MHz左右),说明涤纶在第1,2段(主断裂区前第2,3段)并未发生断裂,可推测主要为涤纶短纤间的摩擦滑移与纤维伸长;涤纶仅在第3段的特征频率概率密度分布曲线分布与第四段(主断裂区)曲线重合较多,呈现纤维开始断裂迹象。
从图8可知,随着拉伸过程的进行,棉纤维的分段概率核心密度值在前3段呈线性增加,在第2段核密度曲线开始部分覆盖表征棉纤维断裂的核心密度值为1.104 MHz,;涤纶的特征频率概率核心密度值在前2段(主峰前第3段和第2段)变化较小,从第3段(主峰前第1段)开始增加,从第3段(主峰前面1段)开始增加并部分覆盖表征涤纶纤维断裂的核心密度值为1.124 MHz,在主断裂区则完全覆盖。结合图6和图7,可初步判断棉纤维在主断裂峰前第2阶段就已经开始断裂,而涤纶的断裂起始于第3阶段。从主断裂区延后5段(即第5至第9段),棉纤维的特征频率概率核心密度值逐段降低,在第9段到第11段则有1次先升后降现象,但其峰值已距离主断裂的核心密度值1 MHz较远,说明涤棉混纺纱中棉纤维断裂时间开始于第2段时间,集中断裂在主断裂区,而后仅有少量纤维补充断裂;而涤纶在第5段到第11段内有2次升高,且第1次升高接近1 MHz,结合图6分析,主断裂区的概率密度峰顶宽而平,表明这一段涤纶的特征频率非常丰富,即涤纶的断裂一直在这一段高密度地发生,且在后续仍有集中断裂的区段,说明涤棉混纺纱中涤纶纤维断裂时间开始于第3段时间,集中断裂在主断裂区及第7段,而后还有1次少量纤维补充断裂。涤纶与棉纤维在涤棉混纺纱拉伸过程中断裂现象符合经典纺织材料学中短纤维纱线拉伸断裂的描述。混纺纱在拉伸断裂过程中不同组分纤维断裂不是同步的,其断裂的先后次序与其材料本身的力学性能有关。
4结论
1)涤棉混纺纱拉伸过程中其组分纤维的声发射信号可以用特征频谱表征,该特征频谱包含涤纶与棉纤维所有的声发射特征频率,且一种纤维的所有特征频率在核心密度值上与其他纤维材料不同;
2)采用核密度估计方法对拉伸过程中涤纶与棉纤维声发射信号的特征频率进行概率密度估计,可知拉伸过程中涤纶断裂的特征频率核心密度值为1.124×106Hz,棉纤维断裂的特征频率核心密度值为1.104×106Hz;
3)涤棉混纺纱拉伸过程的每一个时间段,其组分纤维的声发射特征频谱各不相同,可以用特征频率的核密度估计表征特征频率谱中各频段的出现密集程度;
4)本文从核密度估计角度研究涤棉混纺纱拉伸过程,发现棉纤维比涤纶先发生断裂,集中断裂在主断裂区,而后还有再次发生断裂的现象,说明材料性能的差异与材料拉伸断裂过程中的声发射信号特征频率的核密度估计有关。
参考文献/References:
[1]于伟东.纺织材料学[M].北京:中国纺织出版社, 2006.
[2]HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc R Soc London(Ser A), 1998, 454:903-995.
[3]CHANG C C, HSIAO T, HSU H Y.Frequency range extension of spectral analysis of pulse rate variability based on Hilbert-Huang transform[J]. Medical & Biological Engineering & Computing,2014,52(4):343-351.
[4]李孟源, 尚振东, 蔡海潮, 等. 声发射检测及信号处理[M]. 北京:科学出版社, 2010.
[5]张悦, 杜守军, 张丽梅. 小波奇异性在钢结构损伤检测中的应用[J]. 河北科技大学学报,2010, 31(2): 151-157.
ZHANG Yue, DU Shoujun, ZHANG Limei. Application of wavelet singularity to steel structural damage detection[J]. Journal of Hebei University of Science and Technology,2010, 31(2):151-157.
[6]ABDULLAH M, ALGHAM D, ZHECHKOV D, et al. The use of acoustic emission for bearing defect identificafect size[J]. Mechanical Systems and Signal Processing, 2006, 20: 1537-1571.
[7]SAAD A, RAJAHAMZAHB R I, MBA D. Observations of changes in acoustic emission waveform for varying seeded defect sizes in a rolling element bearing[J]. Applied Acoustics, 2009, 70: 58-81.
[8]焦阳, 侯洁, 李光海, 等. 声发射信号处理技术及其在滚动轴承检测中的应用现状[J]. 河北科技大学学报,2013, 34(4): 313-317.
JIAO Yang, HOU Jie, LI Guanghai, et al. Acoustic emission signal procession technology and its application in rolling bearing test[J]. Journal of Hebei University of Science and Technology,2013, 34(4): 313-317.
[9]薛亚静, 林兰天, 张福乐. 基于AE技术与HHT的环锭纱拉伸断裂过程研究[J]. 河北科技大学学报,2015, 36(1): 47-54.
XUE Yajing, LIN Lantian, ZHANG Fule. Research on fracture process of ring-spun yarn based on AE technique and HHT[J]. Journal of Hebei University of Science and Technology,2015, 36(1): 47-54.
[10]丁利伟, 沈玉娣. 复合材料拉伸过程的声发射特性研究[J]. 无损检测, 2009, 31(10): 781-785.
DING Liwei, SHEN Yudi. Reasearch on acoustic emission characteristics of the composite material during tensile test[J]. Nondestructive Testing, 2009, 31(10): 781-785.
[11]JOSE J, ROSA G, LORET I L, et al. Wavelets and wavelet packets applied to detect and characterize transient alarm signals from termites [J]. Measurement,2006, 39: 553-564.
[12]陈群涛. 基于声振信号EMD和ICA的铣刀状态监测技术研究[D]. 上海:上海交通大学, 2012.
CHEN Quntao. Sound Signal and Vibration Signal Processing for Tool Breakage Monitoring Based on EMD and ICA[D]. Shanghai: Shanghai Jiao Tong University, 2012.
[13]李林洁. EMD和ICA在内燃机振动信号分析中的应用研究[D].天津:天津大学,2012.
LI Linjie.Application of EMD and ICA to Vibration and Acoustion Signal Processing in Internal Combustion Engine[D].Tianjin:Tianjin University,2012.
[14]贾瑞生, 赵同彬, 孙红梅, 等. 基于经验模态分解及独立成分分析的微震信号降噪方法[J]. 地球物理学报,2015, 58(3):1013-1023.
JIA Ruisheng, ZHAO Tongbin, SUN Hongmei, et al. Micro-seismic signal denoising method based onempirical mode decomposition and independent component analysis[J].Chinese Journal Geophsyics, 2015, 58(3):1013-1023.
[15]李存华, 孙志挥, 陈耿, 等. 核密度估计及其在聚类算法构造中的应用[J]. 计算机研究与发展,2004, 41(10):1712-1719.
LI Cunhua, SUN Zhihui, CHEN Geng, et al.Kernel density estimation and Its application to clustering algorithm construction[J]. Journal of Computer Research and Development,2004, 41(10):1712-1719.
[16]谢中华. MATLAB统计分析与应用:40个案例分析[M]. 北京:北京航空航天大学出版社, 2010.
Analysis of acoustic emission signal of polyester/cotton yarns in the moment of tensile fracture by kernel density estimation method
WANG Jin, LIN Lantian, GAO Cong, XIN Binjie, SHEN Yanding
(Fashion College, Shanghai University of Engineering Science, Shanghai 201620, China)
Abstract:To study tensile fracture of various component fibers of polyester/cotton yarns, acoustic emission signal acquisition device is built, which is used to collect the acoustic emission signals of polyester, cotton and polyester/cotton ring spun yarn, respectively. The acoustic emission time domain signal is translated into frequency domain signal by HHT and ICA analysis method, and the frequency and amplitude are extracted. Based on kernel density estimation method, acoustic emission signals of polyester fibers and cotton fibers in the tensile process of polyester/cotton yarns are analyzed. The results show that frequency spectrum can be used to characterize the acoustic emission signals of the component fibers, the difference of characteristic frequency spectrum of acoustic emission signal of various materials can be expressed by kernel density estimation of characteristic frequency in each stage of tensile fracture process, and the fracture order of the component fibers can be deduced.
Keywords:fiber manufacturing technology; polyester/cotton yarn; kernel density estimation; characteristic frequency spectrum; acoustic emission; HHT; ICA; tensile fracture
通讯作者:林兰天教授。E-mail:llt39@126.com
作者简介:王瑾(1989—),女,河南信阳人,硕士研究生,主要从事纺织品检测方面的研究。
基金项目:上海市教委学科建设项目(XKCZ1207)
收稿日期:2015-08-14;修回日期:2015-11-11;责任编辑:张军
中图分类号:TS107.2
文献标志码:A
doi:10.7535/hbkd.2016yx01014
文章编号:1008-1542(2016)01-0083-05
