CRTSⅠ型板式无砟轨道凸形挡台树脂离缝成因分析

苏乾坤，杨荣山

(西南交通大学高速铁路线路工程教育部重点实验室，成都　610031)



CRTSⅠ型板式无砟轨道凸形挡台树脂离缝成因分析

苏乾坤，杨荣山

(西南交通大学高速铁路线路工程教育部重点实验室，成都610031)

摘要：针对目前在桥梁地段CRTSⅠ型板式无砟轨道凸台周围树脂离缝，建立CRTSⅠ型板式轨道力学模型，采用可压缩超弹单元模拟树脂层，分析不同扣件阻力、轨道板与CA砂浆间的摩擦阻力条件下的填充树脂层受力。结果表明：在纵向荷载作用下，一旦树脂层发生塑性变形，随着荷载消失和温度下降，树脂层将无法完全回弹，因而产生离缝，并在梁端转角和列车振动荷载作用下进一步发展；在扣件纵向阻力较大时，树脂层会从轨道板下表面与树脂层相接触的位置剪切破坏；轨道板与CA砂浆层之间的摩擦阻力对树脂层的压缩位移和剪切应力的影响不大。

关键词：CRTSⅠ型板式无砟轨道；凸形挡台；填充树脂；离缝；剪切破坏

1概述

板式无砟轨道作为无砟轨道结构的形式之一，具有传力明确，易于维修等优点。凸形挡台和树脂填充层是板式轨道的重要传力部件，它们承受着轨道板传递的纵、横向力。近年来许多研究者对凸台和树脂的受力进行了研究分析，主要有：桥梁伸缩、挠曲、列车制动和钢轨断轨等工况下凸台的受力[1]；连续梁桥上 CRTSⅠ型板式无砟轨道凸形挡台纵向力分析[2]；树脂弹模对板式轨道凸形挡台受力行为的影响，指出在树脂弹性模量较小时对凸形挡台的受力有利[3]。凸形挡台还可承受冲击荷载，树脂填充层能作为柔性材料有效地减缓冲击，避免了应力集中。

目前我国的CRTSⅠ型框架板式无砟轨道主要被应用在哈大、沪宁城际、广珠、广深港、宁安、哈齐、海南东环等高速铁路上。针对目前CRTSⅠ型板式无砟轨道在运营过程中出现的凸形挡台周围填充树脂离缝问题(较大的离缝达到14 mm，一般发生在桥梁地段梁缝附近，并随着桥梁跨度越大其梁端的离缝值也越大)，建立有限元模型指出了树脂层可能发生破坏的位置，分析离缝产生原因、发展机理。病害现场照片如图1所示。

图1　半圆形凸台与树脂层之间的离缝

2凸台树脂离缝分析及模型原理

在桥梁地段，由于夏天温度高，连续梁下部受热，底座板与梁体刚性连接，梁体活动端膨胀延伸，带动底座板与凸形挡台一起移动，轨道板由于受上部长轨条和扣件限制，不会随着底座板一起移动，故桥梁端部的树脂层就会被压缩；在冬季，随着气温降低，连续梁降温回缩，带动底座板一起回移，本身受压的填充树脂压力得到释放。在树脂层被压缩期间，若在列车荷载作用下发生了塑性变形，那么当回缩量过大时，超过了树脂层的弹性范围，轨道板和树脂层之间就产生离缝，如图2所示。

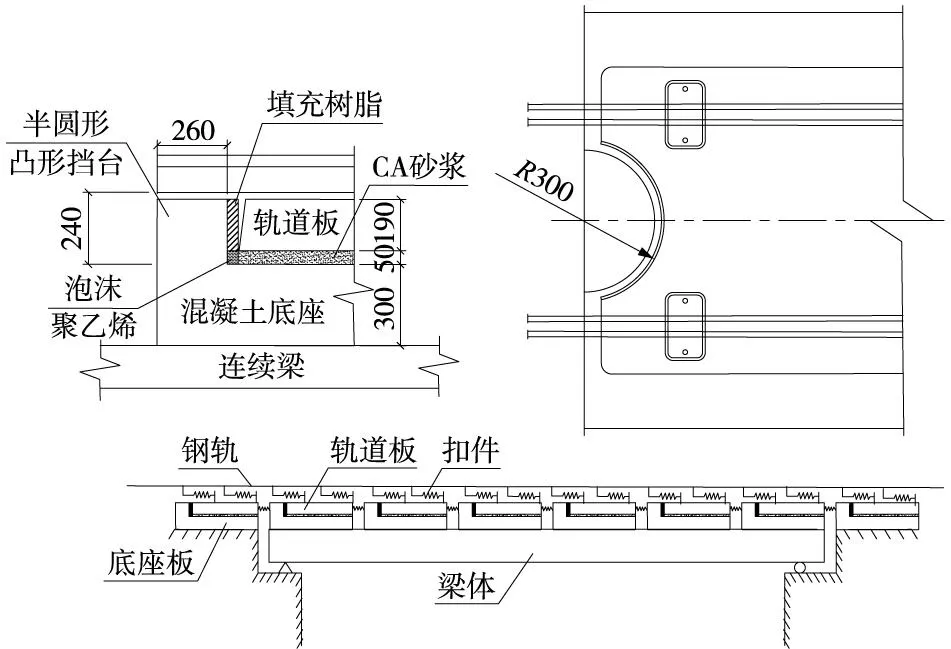
图2　离缝示意(单位：mm)

2.1　力学模型分析

列车荷载对轨道的纵向作用力通过钢轨向下传递，作用在扣件上，然后传递给轨道板，使其产生纵向位移，压缩树脂层，将力传递给CA砂浆层和凸台。轨道板上的力主要有三部分：轨道板与砂浆层之间的摩擦力Fμ，扣件作用力Ff和凸台作用力Fr[4]。这三种作用力之间满足公式

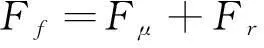
模型的建立中不考虑列车的横向荷载作用，主要进行纵向受力分析。由于桥梁端部铺设的小阻力扣件生锈老化导致纵向阻力增大，失去了小阻力扣件的功效，扣件阻力增大，轨道板的纵向位移也随之增加，从而树脂层的压缩量增加，产生塑性变形。而且由于砂浆材料和施工中的人为不确定因素的影响，以及在运营中所处环境的差异性，CA砂浆和轨道板间的摩擦系数μ不能完全达到设计值。故考虑通过增加扣件阻力，改变轨道板与CA砂浆层之间摩擦系数的方式，分析其对树脂层受力变形的影响。

2.2　有限元模型

本文用有限元软件ANSYS建立1块框架式轨道板，其中底座板、挡台和轨道板均采用实体单元(Solid45)模拟。CA砂浆层的纵向、横向、垂向刚度均采用非线性弹簧单元(Combin39)模拟。高速铁路客运专线凸形挡台与轨道板半圆缺口间填充的聚氨酯树脂，是一种高性能的可室温施工、室温固化成型的聚氨酯弹性体，性能介于塑料和橡胶之间的特种材料[5-9]。考虑到聚氨酯材料的高弹性，为观察树脂层在较大作用力下的局部受力情况，树脂层采用可压缩的实体超弹单元(HYPER86)模拟。树脂层与凸台和轨道板的接触面均采用粘结处理，并对底座板下表面进行全约束[10]。

超弹材料一般用于模拟橡胶和其他许多聚合物材料，通常由应变能密度函数导出超弹材料应力。有限元软件提供两种选项来描述该特性，Mooney-Rivlin选项适用于不可压缩材料，Blatz-Ko选项适用于可压的泡沫灰材料(例如聚氨脂橡胶)。HYPER86单元适用于3-D实体超弹性结构建模，它应用于具有任意大位移和大应变的近似不可压缩的橡胶类材料，可压缩性和不可压缩性材料都可以模拟，本文应变能函数选取Blatz-Ko函数模拟可压超弹材料，典型力与变形曲线如图3所示[10]。

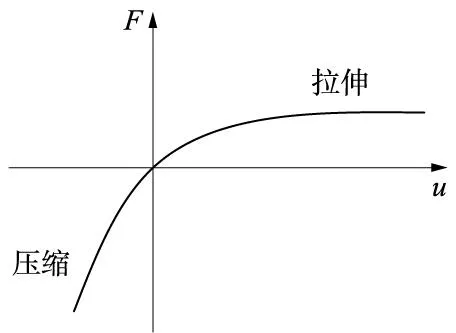
图3　可压超弹材料的典型力与变形曲线

假定一个应变值，超弹材料的应力可以由应变能密度函数(W)与相应的应变分量确定。

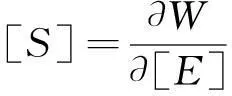
其中，[E]为已知的拉格朗日应变张量；[S]为计算出的第二皮奥拉-克希霍夫应力张量；W为单位体积应变能函数。

在有限元软件中，假定超弹材料是各向同性的，在每个方向都有完全相同的材料特性。在这种情况下，可以根据应变不变量I1、I2和I3来写出应变能密度函数。应变不变量是与坐标系无关的应变表示法，这就意味着已经假设材料是各向同性的，Blatz-Ko应变能密度函数可以用应变不变量表示。材料选项需要的唯一材料常数是初始剪切模量G，剪切模量可由程序中输入的弹性模量和泊松比导出，G=E/(2(1+n))。Blatz-Ko材料的应变能密度函数表示为

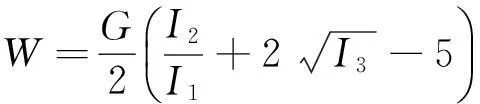
填充树脂弹性系数为10 kN/mm[6]，通过对半圆凸台近似换算，模型中弹性模量取1.76 MPa。假定当轨道板与CA砂浆层之间的相对位移达到0.5 mm时，摩擦阻力达到极限值[11]。建立的有限元模型和半圆形树脂模型如图4所示。

图4　有限元模型和树脂模型

3计算结果与分析

3.1　扣件阻力的影响

每块轨道板上设置8对扣件，当选定阻力扣件后，在列车通过时，车轮通过扣件对轨道板的作用力为单个扣件阻力的16倍。扣件作用力根据扣件阻力的变化而变化，工况参考表1选取[12]，轨道板与CA砂浆层之间的摩擦系数暂取为0.35。

表1　工况

3.1.1树脂层离缝分析

工况4下的填充树脂层的沿线路纵向的压缩位移如图5所示。

图5　工况4填充树脂层压缩量云图

由图5可以看出，填充树脂层压缩位移最大值出现在树脂层中间的上边缘位置。在此得到的位移是树脂层与轨道板之间没有发生分离的，即树脂层受外力作用被统一向前挤压。在树脂层的端部，由于没有受到限制，向前移动量最大，从图中可以看出，端部的位移量与树脂层中间边缘的压缩位移大致相同。将各工况下填充树脂层沿线路纵向的压缩位移提取出来，见表2。

表2　填充树脂层压缩位移

通过表2可以看出，在扣件作用力较小时，树脂层的压缩量较小，控制在弹性范围内。随着扣件作用力增加，树脂压缩量逐渐增加，但增加量逐渐减小，并在工况5后趋于稳定。这是由于树脂层达到一定的压缩量后将发生塑性变形，此时的弹性模量将增大，树脂层更难被压缩。填充树脂层发生塑性变形后，随着桥梁梁体温度的降低，伸缩量减小，作用于钢轨上的作用力也减小，轨道板受力减小，开始回弹，由于此时树脂层已经发生了塑性变形，钢轨带动轨道板回移时，树脂层无法完全回弹，因此产生离缝，且离缝的最初产生位置在树脂层中间的上边缘位置，离缝一旦产生，在纵向力作用下就会沿着树脂层的边缘发展。

列车通过桥梁时，作用于桥面上的列车荷载使梁端发生竖向转角，同时扣件作用力通过轨道板沿纵向不断挤压树脂层，这两种外力叠加起来导致列车通过时产生的振动荷载将填充树脂逐渐向外碾压，再由于树脂材料的固化收缩，加剧了离缝的发展。

3.1.2树脂层破坏分析

凸形挡台周围的填充树脂容易受剪破坏[6]，因此需要提取各工况下的填充树脂的局部剪应力。填充树脂的剪力的较大值都出现在树脂层半圆中线附近，并且随着扣件作用力的增加，剪力最大值出现在轨道板下表面与树脂层相接触的位置，可以推断现场会出现填充树脂层从该处剪断破坏。将各工况下的填充树脂层的最大剪应力提取出来作为纵坐标，以扣件阻力为横坐标绘制关系曲线，如图6所示。

图6　填充树脂层剪应力随扣件阻力变化曲线

从图6可以看出，随着扣件纵向阻力的增大，填充树脂层的最大剪切应力随之增大，由于凸台的限位作用，树脂层最大剪切应力与扣件纵向阻力基本呈线性关系，当扣件阻力增大到15.69 kN/mm时，填充树脂层的最大剪切应力达到2 MPa，这个值已经达到树脂层的抗剪强度。而凸台中性轴的抗剪强度为2.42 MPa，即树脂层会先于凸台发生剪切破坏[11]。需要指出的是，因模型假定树脂层为超弹体材料，几乎不发生塑性变形，而在实际情况中，塑性变形一旦开展，材料的弹性模量将增大，此时同样的外力，填充树脂层所受到的剪力也将增大，因此上文中计算得到的填充树脂层的最大剪应力值偏小。

为研究轨道板下表面与树脂层相接触的位置的剪切应力变化趋势，沿该位置的半圆弧线等距离选取了17个节点，以各个节点在模型中的横向位置为横坐标，相应的剪应力值作为纵坐标，绘制关系曲线，如图7所示。

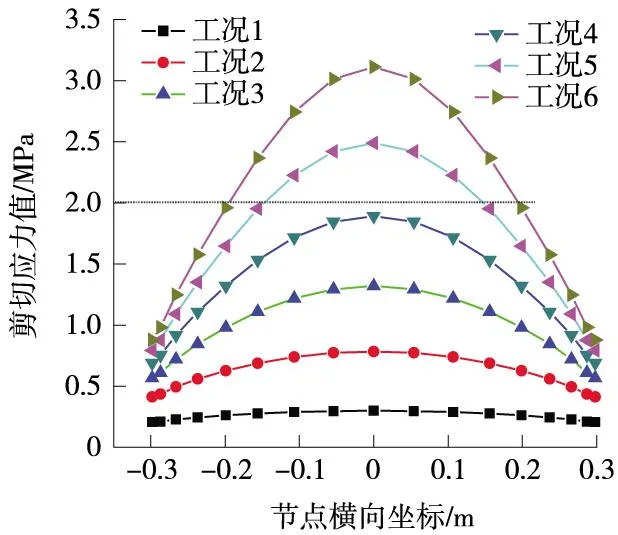
图7　道板下表面与树脂层相接触位置的剪切应力变化趋势

从图7可以看出，轨道板下表面与树脂层相接触位置的剪应力值以轨道板纵向中心线为对称轴左右对称，原因在于扣件作用力也是以轨道纵向中心线为对称轴对称的。选取接触位置的1/4圆分析，可知树脂层端部的剪应力值最小，沿着圆弧线向中心位置剪应力值不断增大，在半圆中线剪应力值达到最大，符合剪切理论。在工况1和工况2条件下，树脂层变形较小，树脂层受力较为均匀；对于工况4～工况6，树脂层半圆中线的剪应力值明显比两侧的大，因为扣件作用力加大后，树脂层沿半圆中线垂向的压缩量增加较快，相对压缩量也增加较快。

树脂层半圆中心上的剪切应力沿树脂层高度的变化趋势如图8所示。可知，树脂层底部所受剪切应力较小，剪切应力值从树脂层底部到轨道板下表面与树脂层相接触位置迅速增大，然后趋于平稳(略微有些减小)，说明剪切应力最大值出现在轨道板下表面与树脂层相接触位置，且破坏面易出现在树脂层半圆中线附近。

图8　树脂层半圆中线剪切应力曲线

3.2　轨道板与CA砂浆层之间摩擦阻力的影响

由于材料和施工中的人为不确定因素的影响，以及在运营中所处环境的差异性，CA砂浆和轨道板间的摩擦系数μ不能完全达到设计值，本文中μ分别取0.20、0.25、0.30、0.35、0.40、0.45、0.50来进行对比分析。扣件阻力取小阻力扣件失效前的扣件阻力4 kN和失效后的扣件阻力8、12 kN来对比分析。以结果中的摩擦系数为横坐标，树脂层的纵向最大位移和最大剪切应力分别为纵坐标，绘制关系曲线如图9所示。

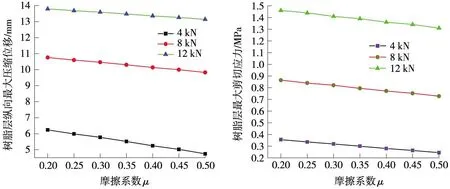
图9　摩擦系数与树脂层的纵向最大位移和最大剪切应力关系

从图9中可以看出，当摩擦系数μ改变0.3，在4、8、12 kN扣件阻力作用下，树脂层的最大压缩位移分别改变1.495、0.932、0.654 mm，树脂层最大剪切应力分别改变0.111、0.136、0.150 MPa。在小阻力扣件失效前，树脂层的压缩量较小；小阻力扣件失效后，即使摩擦系数较大，树脂层也有较大的压缩量。可见，摩擦阻力的改变对树脂层的最大压缩位移和最大剪切应力的影响不大，且树脂层可能发生破坏的位置也并未改变。

4结论及建议

凸形挡台填充树脂层的离缝一般都是由于其塑性变形后产生的，产生塑性变形后的树脂，弹性下降，使用性能将无法满足要求。在纵向荷载作用下，一旦树脂层发生塑性变形，随着荷载消失和温度下降，树脂层将无法完全回弹，因而产生离缝，并在梁端转角、列车振动荷载和树脂固化收缩的作用下进一步发展。在扣件作用力较大时，树脂层会从轨道板下表面与树脂层相接触的位置剪切破坏。此外，为减小梁端凸形挡台填充树脂离缝的产生和发展可以采取以下措施。

(1)改变破损处填充材料的材质，保证强度足够的条件下，适当增加弹性系数，延迟塑性变形的开展，确保轨道板回移时，树脂层能够正常回弹。

(2)小阻力扣件失效后，树脂层的压缩量比较大，易发生塑性变形，故应确保小阻力扣件的正常使用，定期检查桥上小阻力扣件的性能，按桥上无缝线路设计要求调整纵向阻力，防止扣件的绝缘轨距块卡紧轨底导致钢轨不能沿垫板滑动和螺栓的扭矩过大(这都将导致扣件纵向阻力值超过设计值)。

参考文献：

[1]陈杨.桥上CRTSⅠ型板式无砟轨道纵向力分析[D].成都：西南交通大学，2009.

[2]王彪，谢铠泽，张亚爽，等.连续梁桥上CRTSⅠ型板式无砟轨道凸形挡台纵向力分析[J].铁道建筑，2013(3)：117-120.

[3]赵伟，王平，蔡文峰.树脂弹模对板式轨道凸形挡台受力行为的影响[J].路基工程，2009(4)：175-176.

[4]赵国堂.高速铁路无砟轨道结构[M].北京:中国铁道出版社，2006.

[5]郑彦，王文忠.聚氨酯树脂及其应用[J].化学教育，2003(4)：3-5，10.

[6]周文英，韦永继，陈战有.铁路无砟轨道挡台填充聚氨酯树脂的研制[J].化学推进剂与高分子材料，2014(4)：54-58.

[7]王嵩，卢子兴.聚氨酯复合泡沫塑料压缩本构关系[J].强度与环境，2005(4)：22-26，59.

[8]张梅，庞金录，杨光付.高速铁路桥梁用低模量聚氨酯伸缩缝[J].化学推进剂与高分子材料，2011(3)：69-72.

[9]褚洪杰，崔国起，王世斌，等.动力荷载下聚氨酯泡沫材料本构关系研究进展[J].高分子材料科学与工程，2012(5)：157-159，164.

[10]龚曙光，谢桂兰，黄云清.ANSYS参数化编程与命令手册[M].北京：机械工业出版社，2009.

[11]赵伟.单元板式无砟轨道伤损及纵向受力分析[D].成都：西南交通大学，2008.

[12]徐凌雁，赵陆青.板式轨道凸形挡台检算[J].铁道标准设计，2006(S1)：158-162.

The Cause Analysis of Open Joints between Resin Layer and Convex Retaining Platform of CRTSⅠSlab Ballastless Track

SU Qian-kun， YANG Rong-shan

(Key Laboratory of High-speed Railway Engineering of Ministry of Education， Xinan Jiaotong University， Chengdu 610031, China)

Abstract：The open joints between resin layer and convex shape platform of CRTSⅠ slab ballastless track are located on the bridge section. This paper establishes a CRTSⅠ slab ballastless track dynamic model to analyze the longitudinal force of resin layer and simulates the fastening force in different conditions and friction with finite element method to analyze the pressure of resin layer. The results show that when the resin layer experiences plastic deformation on account of the longitudinal force， the resin layer will not be fully rebound along with the disappearance of load and temperature drop， resulting in open joints. And the open joints develop further under the effect of beam-end rotation angle and train vibration load. In case of larger longitudinal resistance， the resin layer is broken by shear at the contact position between the lower surface of the track slab and the resin layer. The change of friction has small effect on the compression displacement and the shear stress of the resin layer.

Key words：CRTSⅠslab ballastless track; Convex retaining platform; Resin layer; Open joint; Shear failure

作者简介：苏乾坤(1992—)，男，硕士研究生，E-mail：947069418@qq.com。

基金项目：国家自然科学基金(51278431)

收稿日期：2015-04-30； 修回日期：2015-06-05

中图分类号：U213.2+44

文献标识码：ADOI:10.13238/j.issn.1004-2954.2016.01.009

文章编号：1004-2954(2016)01-0043-05