基于ANSYS的供球机构摆动轴静动态特性分析

2016-02-29刘劲松姜文庆

电子科技 2016年1期

关键词：动态特性

刘劲松,姜文庆,王　鹤

(1.上海理工大学机械工程学院,上海　200093;2.上海微松工业自动化有限公司,上海　201114)

基于ANSYS的供球机构摆动轴静动态特性分析

刘劲松1,2,姜文庆1,王鹤2

(1.上海理工大学机械工程学院,上海200093;2.上海微松工业自动化有限公司,上海201114)

摘要供球机构摆动轴的静动态特性对稳定供球、提高供球成功率和提高植球良率有着重要意义。因此,有必要对摆动轴静动态特性进行仿真分析。通过建立简化的摆动轴力学模型,并应用有限元分析软件ANSYS对摆动轴摆动角0°中间位置和±45° QUOTE 极限位置进行了静态分析,得到了摆动轴在这些位置的应力、变形云图。对摆动轴进行模态分析,得到了摆动轴前6阶固有频率以及振形。分析结果表明,摆动轴的初步设计符合设计要求,同时判断出摆动角±45° QUOTE 位置是摆动轴危险位置,为植球机供球机构的下一步设计与优化提供了参考。

关键词供球机构;摆动轴;静态特性;动态特性

Static and Dynamic Characteristics of the Swing Shaft ofBall Feeding Mechanism of Ball Mounter

LIU Jinsong1,2,JIANG Wenqing1,WANG He

(1.School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China;

2.Shanghai Pine Industrial Automation Ltd.,Shanghai 201114,China)

AbstractThe static and dynamic characteristics of the swing shaft of ball feeding mechanism is of great significance in the ball feeding stability,the success rate for ball feeding and ball mounting.Therefore,it is necessary to conduct the static and dynamic characteristics of the swing shaft simulation analysis.A simplified swing shaft mechanical model is established and the finite element analysis software ANSYS is used for a static analysis of swing axle swing angle of 0° intermediate position and ±45° limit position to obtain the stress and deformation nephogram of the shaft wobble at these positions.The modal analysis of the swing shaft is carried out,and the natural frequency and the vibration form of the first six natural frequencies are obtained.The results show that the preliminary design of the swing shaft meets the design requirements and that the swing angle±45° position is the dangerous position.It provides references for the subsequent design and optimization of the ball mechanism.

Keywordsball feeding mechanism;the swing shaft;static characteristics;dynamic characteristics

植球机是半导体封装技术的关键设备之一,主要由印刷系统、植球系统、检查系统、上料系统和下料系统组成[1]。植球系统主要完成均匀、准确地将焊锡球放置于精密模板的动作,为下一步的锡球拾取做好准备。供球机构是植球系统的核心部件,其焊锡球的供给、焊锡球的放置和多余焊锡球的回池3大主要动作全部需要借助摆动轴的周期性摆动来完成。由于植球机使用的焊锡球的球径较小、质量很轻,所以对摆动轴静动态性能要求高[2]。文献[3]研究了供球机构在两种不同加减速控制方式下运动学特性,但没有对静刚度、频率、振形这些对供球机构静动态特性有直接影响的因素进行分析,且没有相关文献对供球机构的这些因素进行分析研究。因此,有必要采用有限元分析手段对植球机供球机构摆动轴进行静动态特性分析,以指导植球机供球机构的下一步设计和优化。

1供球机构结构组成

供球机构几何模型如图1所示,为完成焊锡球的供给、放置和回池动作,需要翻板可靠、稳定地作±45°翻转动作[4],从而要求摆动轴做摆动角为-45°~+45°的周期性转动。动力通过同步带由伺服电机输入。伺服电机一般采用T型加减速控制方式,摆动轴在T型加减速方式下伺服电机角速度表达式如式(1)所示。

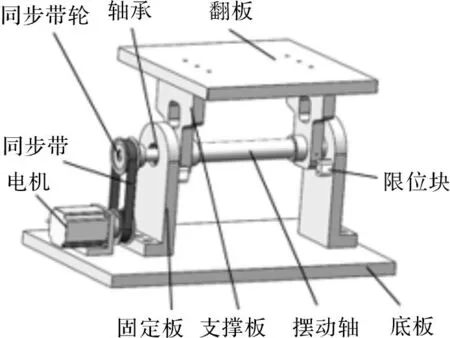
图1　植球机供球机构几何模型

(1)

其中,ω(t)是摆动轴的角速度;t为时间,单位为s。

2供球机构摆动轴有限元模型建立

对结构进行有限元分析,没有必要完全按照物理模型进行建模,对摆动轴的模型中的倒角、圆角、退刀槽进行简化处理,以提高计算分析效率。

文献[5]显示将摆动轴简化成梁单元进行有限元分析,不仅运算效率更高,且结果也更接近物理实验结果。ANSYS提供的Beam188梁单元适合本文中摆动轴进行有限元建模。Beam188是三维线性有限应力梁,基于Timoshenko梁理论,考虑了剪切变形的影响。摆动轴的材料为合金结构钢,密度7 800 kg/m3,弹性模量206 GPa,泊松比0.3。轴承的接触刚度对摆动轴的静动态特性有一定影响,不可忽略。可在轴承支承处沿圆周方向均布4个弹簧单元来模拟轴承,ANSYS中提供了弹簧单元Combine14,该单元具有一维、二维或三维应用中的拉伸或扭转的特性,弹簧单元布置方式如图2所示[6]。

图2　轴承接触等效模型

考虑到摆动轴轴承采用两端固定支承,对弹簧的P1、P2、P3、P4节点约束其所有自由度,对P5、P6、P7、P8节点施加轴向零位移约束。弹簧单元的长度为轴承的内外圈半径之差,弹簧刚度为轴承的径向刚度,轴承的径向刚度可根据轴承的相关参数依据经验公式计算[7]。

摆动轴的支承轴承采用日本Misumi公司的深沟滚珠轴承,轴承型号为SB6905ZZ,相关参数如表1所示。

表1　MISUMI SB6905ZZ轴承相关参数

深沟球轴承径向刚度经验计算公式

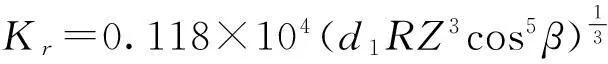
(2)

式中,F为径向载荷,每个轴承的径向载荷为摆动轴、支撑板和刮板组件等重量的1/2;Z为为滚动体数目;β为滚动体接触角;d1为钢球直径。入轴承相关参数,经计算得Kr=2 367N/μm。

3摆动轴静态分析

由于摆动轴做作摆动角为-45°~+45°的周期性动作,存在两个摆动角±45°极限位置和一个摆动角0°的中间位置,两个摆动角±45°的极限位置的受力情况相同,所以可只分析其中一个位置。为简化计算,只分析摆动角0°位置和摆动角+45°位置的受力情况,对于摆动轴的其他位置,假设其受力情况均介于摆动角0°位置和摆动角+45°位置受力情况之间。

3.1　摆动轴摆动角0°位置静态分析

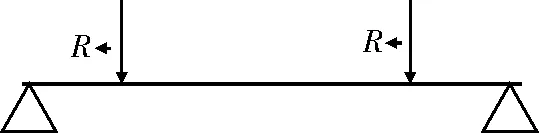
图3　摆动角0°位置摆动轴受力简图

当摆动角0°位置时,此时摆动轴受力情况可简化成只承受自身重力g和来自支撑板等零件的重力而产生的径向载荷R[8],经计算R=75.35 N。使用ANSYS分析,得到摆动轴的挠度、应力云图如图4所示。可看出摆动轴在摆动角0°情况下最大挠度为3.6×10-4mm,发生在摆动轴中间位置处。最大应力为0.78 MPa,发生在轴承支承内侧边缘处。

图4　摆动角0°位置摆动轴变形、应力云图

3.2　摆动轴摆动角+45°位置静态分析

图5　摆动角+45°位置摆动轴受力简图

当摆动角+45°位置时,此时摆动轴受力情况可简化成承受自身重力和来自支撑板等零件的重力而产生的径向载荷R和扭转力矩T,经计算R=75.35 N,T=1 130.25 N·mm。使用ANSYS分析,得到摆动轴的挠度、应力云图如图6所示,摆动轴在摆动角+45°时最大挠度4.2×10-4mm,发生在摆动轴中间位置处。最大应力为0.93 MPa,发生在轴承支承内侧边缘处。

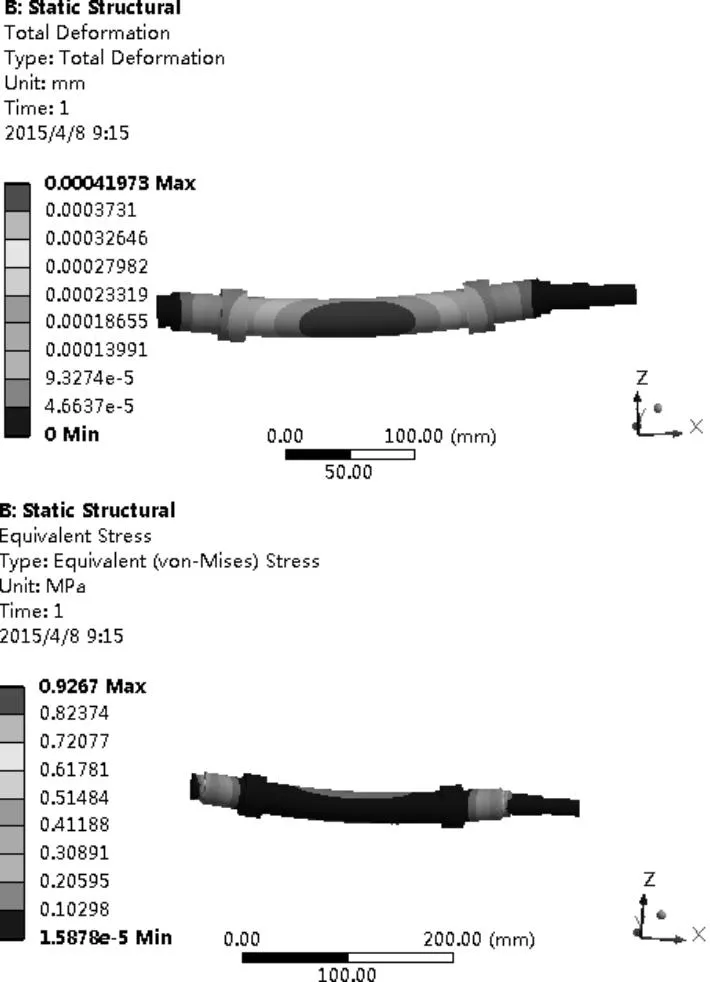
图6　摆动角45°位置摆动轴变形、应力云图

经过对摆动轴摆动角0°位置和摆动角+45°位置进行静态分析,可得出摆动角±45°位置的摆动轴扰度和应力均大于摆动角0°位置的摆动轴挠度和应力,摆动角±45°位置是摆动轴的危险位置。最大挠度为4.2×10-4mm发生在摆动轴的中间轴段,小于设备精度要求的0.005 mm。最大应力0.93 MPa发生在轴承支承内侧边缘截面,远小于材料的屈服强度,因此轴的静态特性符合设计要求。

4摆动轴动态特性分析

有限元方法的动态分析主要包括模态分析、谐响应分析、响应谱分析、随机震动分析等,其中模态分析[9]是计算结构震动特性的数值技术,结构振动特性包括固有频率和振形。摆动轴的振动特性对植球最终效果有着重要的影响。因此,本文主要研究摆动轴的固有频率和振形。

采用子空间迭代法对供球机构摆动轴前6阶振动特性进行分析研究。经过分析计算,得出摆动轴前6阶固有频率和振形。

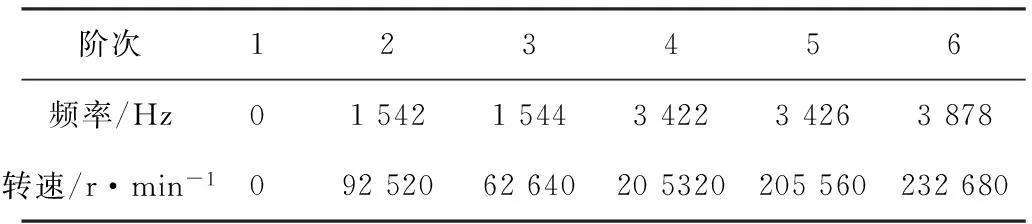
表2　摆动轴前六阶固有频率

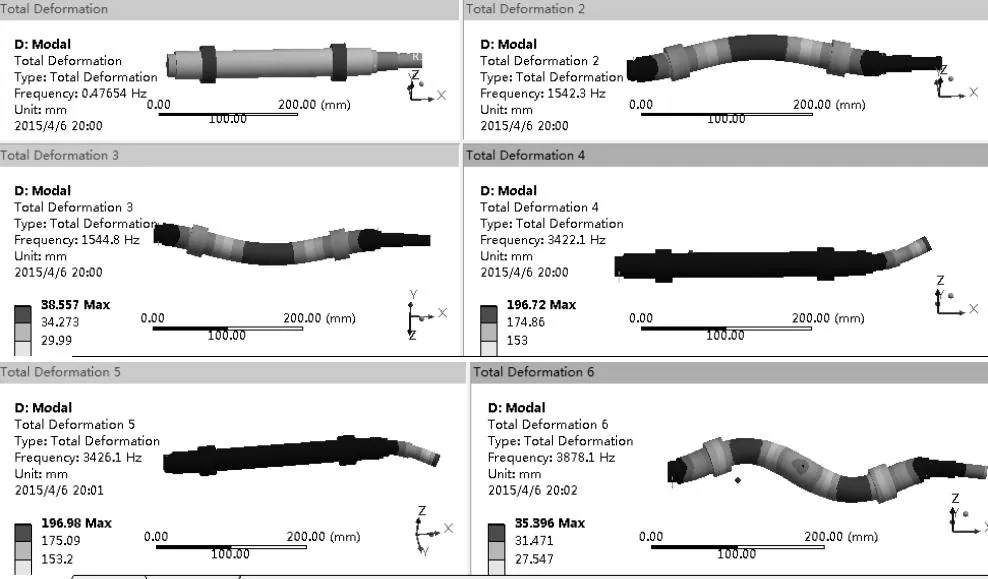
图7　摆动轴前6阶振形

根据传动轴的稳定性理论,当转速n满足13n1≤n≤0.7n2(n1、n2分别为1阶、2阶临界转速)时,转轴是柔性轴,可在一定范围内稳定运行[10]。摆动轴在T型加减速控制方式下的最高转速为n=20×3.14×60=3 768 r·min-1,符合柔性轴条件。因此,摆动轴为柔性稳定轴,不会有共振的危险。

5结束语

(1)对摆动轴处于摆动角0°位置和+45°位置分别进行了静态分析,对比得出了摆动角±45°位置是转

轴周期摆动危险位置结论。同时,找到了最大挠度4.2×10-4mm和最大应力的发生截面为轴承支承内侧边缘处截面;(2)对摆动轴的模态分析,获得了前6阶固有频率和振形,根据传动轴理论判定摆动轴为柔性稳定轴,在现有转速下不会发生共振;(3)有限元分析的结论,为植球机供球机构的设计和优化打下了基础。

参考文献

[1]刘劲松,郭俭.BGA/CSP封装技术的研究[J].哈尔滨工业大学学报,2003(5):602-604.

[2]方兴.用于集成电路阵列(BGA)封装的全自动植球机的研制开发[D].合肥:合肥工业大学,2005.

[3]夏链,吴斌,田晓青,等.基于虚拟样机的BGA供球机构动态性能仿真研究[J].合肥工业大学学报:自然科学版,2013,36(8):910-914.

[4]夏链,韩江,方兴,等.球栅阵列(BGA)自动植球机的研制[J].仪器仪表学报,2006(27):155-158.

[5]蔡力钢,马仕明,赵永胜,等.多约束状态下重载机械式主轴有限元建模和模态分析[J].机械工程学报,2012(2):165-173.

[6]王德帅.考虑轴承摩配间隙的高速电主轴静动态特性分析[D].哈尔滨:哈尔滨工业大学,2014.

[7]刘悦,汪劲松.基于轴承及导轨接触刚度的混联机床静刚度研究及优化[J].机械工程学报,2007(43):151-154.

[8]范钦珊,蔡新.工程力学[M].2版.北京:机械工业出版社,2012.