基于随机几何理论的多小区协作网络分析

蔡 杰，刘 陈，陆 峰

(南京邮电大学 电子科学与工程学院，江苏 南京 210046)

基于随机几何理论的多小区协作网络分析

蔡 杰，刘 陈，陆 峰

(南京邮电大学 电子科学与工程学院，江苏 南京 210046)

多小区协作技术能够解决拥堵蜂窝网络中小区边缘用户通信质量较差的问题,但是目前维纳模型无法准确分析该技术对蜂窝网络的影响。所以为了合理分析多小区协作技术带来的性能提升，文中提出利用泊松点过程的方法对蜂窝小区进行建模。在该模型下利用随机几何工具，分析了下行链路和上行链路中使用多小区协作技术情况下的覆盖概率，得到了覆盖概率准确数学表达式和该技术所能提供的增益。通过分析发现，使用多小区协作技术能明显提升小区的覆盖能力。并且随着协作越充分，该技术带来的增益越大。

蜂窝网络；多小区协作；泊松点过程；覆盖概率；随机几何

1 概 述

现代社会手机用户数量爆发式的增长使得各蜂窝网络中的上行链路和下行链路信道堵塞。这种情况下，蜂窝小区的小区内部及小区间干扰就成为了制约整个无线通信网络吞吐量的重要因素。因此如何制约和减轻干扰信号对手机用户通话质量的影响就成为了设计新一代无线通信系统的重要因素。

多小区协作技术允许多个基站同时为一个用户提供服务，从而抑制干扰信号、提高通信质量。但是这种质量的提高需要消耗大量网络资源，这些基站组要通过光纤或者其他反馈链路将来自同一个用户的信号传给数据中心进行进一步的处理[1]。所以考虑到网络资源和数据处理能力的消耗，多小区协作并不适合广泛应用于整个空间中的所有用户。在现实情况中，由于手机终端设备发送功率的不断提高和信号编码技术的应用，处于小区中间的普通用户通话质量能够得到保障，但是考虑到处于小区边界的手机用户距离周围基站较远，信道状况较为恶劣，其通话质量受到干扰信号的影响较大。所以为了改善这一情况，处于小区边缘位置的用户可以使用多小区协作技术。因此文中的分析对象是蜂窝小区的边缘用户[2]。

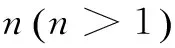
基于以上假设，对于下行链路中某小区边缘用户，它能同时接到来自这n个服务基站的有用信号。而在上行链路中，该用户能够将信号同时发送给这n个服务基站。

近年来，多小区协作技术被广泛研究。但大部分论文均使用在分析通信系统中最常用的维纳模型(Wynermodel)对整个蜂窝网络进行建模。例如，文献[3-7]就利用维纳模型对在下行链路中使用多小区协作技术进行了详细分析。

维纳模型是一个易于分析但是过于理想化的模型。维纳模型中，认为用户到基站之间的信道为理想信道，小区内干扰是一个常数，而小区间干扰可以忽略不计。但是在现实情况中，由于空间中的手机用户增多导致小区间的信号干扰增加，所以小区间干扰不能忽略不计。而且随着空间中手机用户密集程度的变化，小区内部的干扰也会产生变化，所以将小区内干扰信号假设成常数也是过分理想化了。维纳模型的另一个缺陷是，它假设空间中的所有蜂窝都是严格的正六边形或矩形。但是在实际情况中蜂窝小区的形状却是随机的。所以传统的维纳模型不再适合分析现代复杂的无线通信系统[8-9]。

由于维纳模型众多缺陷的存在，使得很多研究者开始使用随机几何模型来描述现代通信网络的拓扑结构。随机几何模型认为空间中的所有基站和用户都是随机分布的，这样就能很好地符合当代手机用户随机分布于整个空间中的实际情况。文献[10-12]使用随机几何模型分析随机选择的某小区边缘用户在上行链路和下行链路中获得的信干比时，利用现代随机几何理论提供的一系列有效工具得到相比于维纳模型更简洁且更精确的分析结果。

由于文中的目标是为了能够更加准确地分析出对于某个使用多小区协作技术的小区边缘用户，在上行链路和下行链路的通话质量。所以选择了随机几何理论中的泊松点过程模型进行建模和分析，并且使用文中提出的根据小区边缘用户的位置动态选择协作基站的策略，在不限定协作基站数目的情况下，得到了上行链路和下行链路的覆盖概率通用数学表达式。

2 下行链路

在蜂窝网络的下行链路中，假设整个空间中的基站(BSs)分布服从强度为λd的泊松点过程(PPP)Φd。对于一个随机选择的小区边缘用户，由于文中分析的场景为整个平面，所以可以不失一般性地认为该用户处在平面的原点位置。将下行链路覆盖概率定义为，某用户收到的有用信号功率和干扰信号功率比值(Signal-to-InterferenceRatio，SIR)大于某个门限值概率。其数学表达式可以写为：

(1)

其中,Pd代表用户收到的有用信号功率;Ij代表用户收到的干扰信号功率;T代表门限值。

2.1 下行链路多小区协作系统模型

对于下行链路信道，使用文献[12]提出的标准功率衰落模型对其进行建模。在下行链路中，定义路径衰落指数为α(α>2)。对于第i个服务基站到处于原点的用户之间的距离用Ri表示。由于文中使用的模型中基站位置是随机分布的，所以Ri为随机变量。假设对于基站和特定用户之间的信号传输只受到均值为1的瑞利衰落的影响。所有基站的发送功率持续且稳定，并且基站发送功率的均值为1/μ。

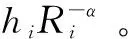
根据之前的假设可知，对于特定的小区边缘用户来说，他收到的有用信号功率是其收到的来自于距离其最近的n个基站信号功率的线性叠加[13]，所以该用户收到的有用信号功率的表达式为:

(2)

而其收到的干扰信号就是来自于空间中所有的干扰基站[14]，所以干扰信号功率的表达式为：

(3)

其中，Rn表示最远的第n个服务基站到位于原点的特定用户之间的距离；β(0,Rn)表示以原点为圆心、Rn为半径的圆域。可以认为在β(0,Rn)之外的点距离原点的距离均大于Rn，所以Φβ(0,rn)这个点集内的点j代表的是干扰基站的位置。参数Dj代表处在j点位置上的干扰基站到原点用户的距离。

又根据泊松点过程的性质可知，在某个点集中删去有限个点后，该点集仍服从泊松点分布，所以Φβ(0,rn)这个点集仍服从泊松点过程分布。根据下行链路覆盖概率定义，可以得到其数学表达式为：

又根据帕斯瓦尔定理可知：

P[pd>(IrT)]=

(5)

其中，符号L表示对随机变量求拉普拉斯变换。

由式(4)、(5)可知，上行链路覆盖概率是由用户到各服务基站之间距离Ri的概率密度函数fRi(rt)，以及用户收到的有用信号功率和干扰信号功率的拉普拉斯变换这两个参数所决定。下两节将分别计算这两个参数。

2.2 服务基站和用户之间距离的概率密度函数

根据前面的分析可知，用户所选择的服务基站是距其最近的n个基站，而随机变量Ri则是描述第i个服务基站到目标用户之间的距离。那么根据分布函数的定义可知，随机变量Ri的分布函数表达式为：

FRi(r)=P{Rir}

P{Ri>r}=

P{在圆域β(0,r)中至多只有i-1个点}=

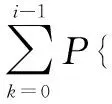
其中，Λ(r)代表泊松点过程在圆域β(0,r)内点分布强度的度量。

根据泊松点过程的定义，其表达式为：

所以根据概率密度函数定义，可得到某特定用户到第i个服务基站距离的概率密度函数表达式为：

2.3 干扰信号与有用信号功率的拉普拉斯变换

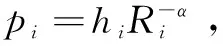
(7)

又根据拉普拉斯变换的性质可得随机变量pi的拉普拉斯变换为：

Fpi(s)=

(8)

对于用户来说，其收到的有用信号的功率为来自各基站信号功率的线性叠加：

同时又由于pi是独立随机变量，根据卷积定理可以得到随机变量Pd的概率分布函数为:

fpd(x)=fp1(x)*fp2(x)*…*fpi(x)*…*fpn(x)

由此，根据拉普拉斯变换的定义可知：

(9)

下行链路中小区间干扰信号功率Ir的拉普拉斯变换根据

文献[12]可知：

(10)

将式(6)、(9)、(10)带入式(4)便可得到下行链路覆盖概率的数学表达式。

3 上行链路

3.1 上行链路系统模型

在上行链路中，某随机选择的小区边缘用户能够将信号发送给距其最近的n个基站。为了便于分析，定义对于使用多小区协作技术的小区边缘用户上行链路，该用户将信号同时发送给n个基站，这n个基站中至少有m(1≤m≤n)个收到的来自该用户的信号功率和该基站收到的干扰信号功率之比(SIR)大于某一门限时，就认为该用户的上行链路被覆盖。

同时对于上行链路来说，手机的发送功率受到本身硬件的制约，所以上行链路的发送功率控制是分析覆盖概率必不可少的考虑因素。文中认为手机的发送功率与该手机距目标基站之间的距离成正比，比例常数为k。因此可以认为对于距离越近的目标基站，手机的上行链路发送功率越小。

在多小区协作中，考虑小区边缘用户所处的信道条件较差。所以为了保证上行链路的通信质量最好，假设手机的发送功率是由用户到距其最远的第n服务基站之间的距离决定的。本节依旧使用Ri代表用户到其第i个服务基站的距离。所以某小区边缘用户的发送功率由Rn决定。虽然这样会造成手机的发送功率过高，但是考虑到用户处于小区边缘位置的时间不可能太长，所以可以认为这样的假设是合理的。

对于上行链路信道的建模，同样使用与下行链路相同的由文献[12]提出的标准功率衰落传播模型。考虑到上行链路是否覆盖的判断标准为至少m个基站收到足够大的有用信号功率，并且同一用户对n个服务基站的发送功率均相同，所以可以合理地认为只要第m个基站收到足够大的有用信号功率，那么就可认为对于使用多小区协作技术的某小区边缘用户，其上行链路被覆盖。所以对于上行链路，文中的分析目标为该用户的第m个服务基站。

3.2 上行链路覆盖概率

假设整个空间中的手机用户分布服从强度为λu的泊松点过程Φu。在整个空间中，可以不失一般性地认为特定用户的第m个服务基站处于空间的原点。对于处于原点的基站，其收到的来自特定用户的信号功率可以表示为：

(11)

其中，hm表示用户到其第m个服务基站的信道，且服从均值为1/μ的指数分布。

虽然该用户不再处于原点位置，但是他与其服务基站的相对位置并未改变。所以Rn，Rm的概率密度函数依旧符合式(6)。

(12)

分析第m个服务基站收到的干扰信号。考虑到文中分析范围为整个空间，小区边缘用户数量只占空间中所有用户的很小一部分，并且小区边缘用户距离所有基站的位置都较远，所以可忽略小区边缘用户的信号对特定基站产生的干扰。本节只用考虑小区内普通用户对于特定基站的干扰。

基于以上分析可知，对于特定小区边缘用户的第m个服务基站来说，其收到的干扰信号功率为整个空间中普通用户发送信号功率之和。又根据泊松点过程中删去有限个点不改变泊松点过程分布的性质，可以认为这些空间内普通用户依旧服从强度为λu的泊松点过程Φu。由于文中假设小区内的普通用户并不使用多小区协作，而是只与距其最近的基站进行通信。所以处于p点的小区普通用户到距其最近的基站之间的距离用Bp表示，而p点到原点(目标基站)的距离用Dp表示。所以目标基站收到的干扰功率为：

(13)

根据上行链路覆盖概率的定义得，上行链路覆盖概率表达式为：

此处考虑分子分母上同时存在参数k，可消去。

又根据拉普拉斯变换性质和hm～exp(μ)可知：

(15)

根据文献[13]可知，上行链路干扰信号的拉普拉斯变换为：

(16)

(17)

其中，式(16)是根据hm～exp(μ)得到的；式(17)是根据泊松点过程的概率生成泛函(PGFL)求得的。

式(17)中积分的上下界表明空间中的所有普通用户均视作某小区边缘用户上行链路的干扰用户。而根据文献[13]可知，对与某用户最近的基站是随机分布于某用户的Voronoi图中的，所以随机变量BP的概率密度函数依旧符合式(6)，表达式为：

(18)

最终将式(18)依次带入式(14)就可得到上行链路的覆盖概率最终表达式。

4 数学分析

本节利用上两节推导出的结果进行Matlab仿真[15]，并分析结果。以下如无特殊说明均假设路径损耗因子α=4。

在下行链路中，认为某小区的边缘用户能够收到来自一个基站组所发送的信号。为了便于分析，只考察n=2,3,4的简单情况。该基站组对于某小区边缘用户的覆盖概率随信干比门限的变化如图1所示。

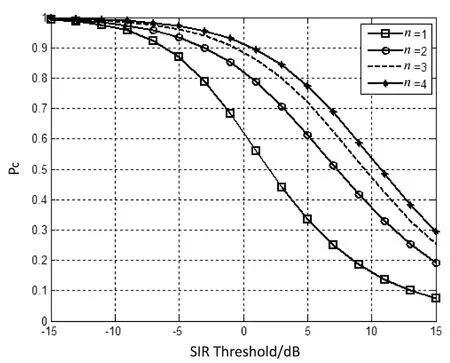
图1 下行链路覆盖概率

由图1可见，由于小区用户能够收到来自多个基站的信号，其下行链路覆盖概率能够得到明显的提升，且随着选择的协作基站的数目越多，其覆盖概率的提升越明显。

在上行链路中，文中假设对于小区内的某个边缘用户来说，它会选择不同数量的协作基站，并且同时为了能够比较，选择最近的基站作为分析的上行链路目标基站(m=2，3)。在实际情况中，由于手机本身功率的限制，上行链路中不能选择过多的服务基站，所以也只考虑n=3,4的情况。得到的上行链路覆盖概率随着信干比门限T的变化如图2所示。

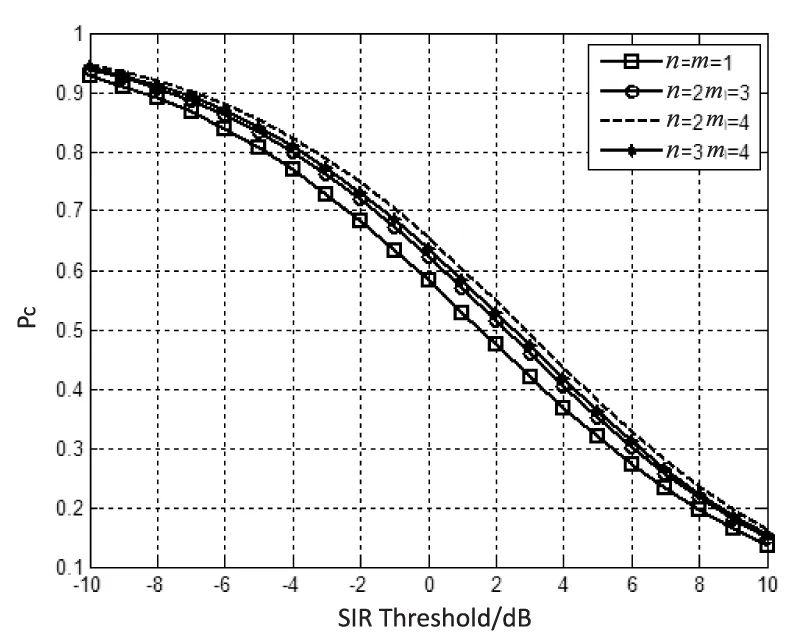
图2 上行链路覆盖概率

从图2可以看出，由于在上行链路中采用了多小区协作技术，上行链路中手机用户对于目标基站的覆盖概率随着选择的基站数目增加而增加，这是为了尽可能多地覆盖所选择的目标基站而增大手机的发送功率所引起的。

5 结束语

文中提出了一种基于随机几何理论的框架，对使用多小区协作技术的蜂窝网络的上行链路和下行链路分别进行建模，重点讨论了利用泊松点过程的数学性质推导对于小区内的随机选择的任意用户，在使用多小区协作技术的情况下，上行和下行链路覆盖概率具体的数学表达式。该式能够适用于分析任意位置小区边缘用户的覆盖概率。分析了在使用多小区协作的情况下，小区中边缘用户的上行和下行链路的覆盖概率。相较于不使用多小区协作，用户只和距离其最近基站通信的情况，使用多小区协作能够提升上行和下行链路的覆盖概率，达到了提升小区边缘用户通信质量的目的。

[1] 史 聃,朱近康.分布式天线小区协作通信系统下行链路频谱效率的研究[J].中国科学技术大学学报,2009,39(5):479-483.

[2] 骆 纯.LTE-AdvancedCoMP中联合处理技术及系统性能研究[D].武汉:武汉理工大学，2010.

[3]WynerAD.Thewiretapchannel[J].BellLabsTechnicalJournal,1975,54(8):1355-1387.

[4]ShamaiS,ZaidelB.Enhancingthecellulardownlinkcapacityviaco-processingatthetransmittingend[C]//Procof53rdIEEEvehiculartechnologyconference.[s.l.]:IEEE,2001:1745-1749.

[5]SomekhO,ZaidelB,ShamaiS.Sumratecharacterizationofjointmultiplecell-siteprocessing[J].IEEETransactionsonInformationTheory,2007,53(12):4473-4497.

[6]JingS,TseDNC,SoriagaJB,etal.Multicelldownlinkcapacitywithcoordinatedprocessing[J].EURASIPJournalWirelessCommunicationsandNetworking,2008,2008:586878.

[7]WynerAD.Shannon-theoreticapproachtoaGaussiancellularmultiple-accesschannel[J].IEEETransactionsonInformationTheory,1994,40(11):1713-1727.

[8] 吕星哉,王 振,朱近康.三角形蜂窝小区的遍历信息论容量分析[J].电子与信息学报,2008,30(4):801-804.

[9]ElSawyH,HossainE,HaenggiM.Stochasticgeometryformodeling,analysis,anddesignofmulti-tierandcognitivecellularwirelessnetworks:asurvey[J].IEEECommunicationsSurveys&Tutorials,2013,15(3):996-1019.

[10]HaenggiM,AndrewsJ,BaccelliF,etal.Stochasticgeometryandrandomgraphsfortheanalysisanddesignofwirelessnetworks[J].IEEEJournalonSelectedAreasinCommunications,2009,27(7):1029-1046.

[11]AndrewsJ,BaccelliF,GantiR.Atractableapproachtocoverageandrateincellularnetworks[J].IEEETransactionsonCommunications,2011,59(11):3122-3134.

[12] 李国通,仇佩亮,徐绿洲.FDD-CDMA的下行链路的波束形成[J].电子学报,1999,27(12):76-79.

[13]NovlanTD,DhillonHS,AndrewsJG.Analyticalmodelingofuplinkcellularnetworks[J].IEEETransactionsonWirelessCommunications,2013,12(6):2669-2679.

[14] 郭 健,郑迺铮,谈振辉.LTE-A上行CoMP软信息合并接收算法[J].电信科学,2012(8):53-57.

[15] 余金蓉.多小区协作系统的仿真实现及性能分析[J].计算机技术与发展,2013,23(11):258-260.

Analysis of Multi-cell Coordination Network Based on Stochastic Geometry Approach

CAI Jie,LIU Chen，LU Feng

(School of Electronic Science and Engineering，Nanjing University of Posts and Telecommunications，Nanjing 210046，China)

In response to the problem of poor communication quality suffered by edge residential users in congested cellular network,one of feasible methods is to employ multi-community collaboration technology.But now the Wyner model cannot analyze this technology accurately.In this paper,the Poisson point process is used to model the cellular community,which is able to accurately analyze communication quality of users in the scenario of edge residential users employing multi-community collaboration technology.The accurate mathematical expressions of coverage probability in uplink and downlink regarding any user within the community are calculated using stochastic geometry tools.The result shows the multi-community collaboration technology can heavily promote the coverage ability.With the adequacy of collaboration,it can bring more enhancement in coverage ability.

cellular network;multi-cell coordination;Poisson point process;coverage probability;stochastic geometry

2015-09-15

2015-12-23

时间：2016-05-25

国家自然科学基金资助项目(61372126，61302101)

蔡 杰(1991-)，男，硕士研究生，研究方向为智能信号处理；刘 陈，博士生导师，教授，研究方向为无线通信中的信号处理、空时编码；陆 峰，副教授，研究方向为随机几何理论。

http://www.cnki.net/kcms/detail/61.1450.TP.20160525.1709.046.html

TN929.5

A

1673-629X(2016)06-0200-05

10.3969/j.issn.1673-629X.2016.06.045