基于小波包基与能量熵的MEG自动分类方法

张学军,丁钰涵,黄丽亚，成谢锋

(1.南京邮电大学 电子科学与工程学院，江苏 南京 210003；2.江苏省射频集成与微组装工程实验室，江苏 南京 210003)

基于小波包基与能量熵的MEG自动分类方法

张学军1,2,丁钰涵1,黄丽亚1,2，成谢锋1,2

(1.南京邮电大学 电子科学与工程学院，江苏 南京 210003；2.江苏省射频集成与微组装工程实验室，江苏 南京 210003)

脑磁信号中包含许多与精神疾病相关的生理信息，是判断神经系统出现各种异常活动的重要依据，对脑科学的研究具有十分重要的意义。为了提高正常人与精神分裂症患者的MEG数据的分类精度，文中提出了一种基于小波包基与能量熵的脑磁特征提取与识别的方法。该方法首先将经PCA降维后的MEG数据进行小波包分解，并结合小波熵从小波包库中选择最优小波包基，然后对选出的最优基所对应的小波系数进行幅度调制求取能量熵，并求取包络能量熵的统计特性构成分类特征向量，最后输入到SVM分类器，实现MEG数据的自动分类。实验结果表明，该方法的分类准确度可达到97.586 8%。说明文中提出的特征提取方法能够有效提取脑磁信号的特征，提高分类精度；也将为精神分裂症的诊断和严重程度的评估提供选择依据。

脑磁信号；小波包分解；幅度调制；能量熵；支持向量机

0 引 言

脑磁图(Magnetoencephalography,MEG)是一种无创伤地探测大脑电磁生理信号的脑功能检测技术，在进行脑检查时探测器不需要固定于患者头部，检测设备对人体无任何副作用。与脑电图反映脑的电场变化不同，MEG反映的是脑的磁场变化。脑磁图不受颅骨的影响，图像清晰易辨，加之对脑部损伤的定位诊断比脑电图更为准确，故对脑部疾病的诊断发挥了其特有的作用。

特征提取是对脑信号进行识别的关键技术之一。在对不同脑信号进行识别时，如果提取的信号特征显著就能获得较高的分类精度。目前常用的特征提取方法有时域﹑频域和时频域结合的分析方法[1-8]。与单一的时域或频域分析方法相比，时频域结合的分析方法能够提供更多的分类信息，因此人们常把时频域结合的分析方法用于生理信号的特征提取中。文献[2]提出了混沌分析和小波包变换相结合的特征提取方法。文献[3]采用基于互信息的特征提取方法。文献[5]将样本熵(或近似熵)应用到具有短时序列特性的生理信号分析中，实现对生理信号的时频分析。

将熵与小波包变换结合是目前常用的分析生理电信号的特征提取方法。王登等[9]使用小波包分解与小波包熵结合的特征提取方法对五类不同脑思维任务进行分类的平均分类准确率高于传统的小波包分解算法。王攀等[10]将小波变换与时域能量熵结合，发现该特征提取方法有较好的分类效果及较短的分类系统运算时间。

在MEG信号的特征分类中获得稳定的神经网络是非常困难的，因为其通常需要选择合适的隐藏层和神经元数目来逼近解决问题的函数所需要的精度。如果网络中样本的数目太多会导致训练数据的过度拟合，进一步导致泛化能力下降。支持向量机(Support Vector Machine，SVM)不仅有稳定的统计学习理论，同时保证训练数据有最优的决策函数[11]。它的优点在于通过最大化网络的性能以及降低学习机的复杂度来平衡准确度。现有的方法在特征提取部分都是对小波包变换或者小波变换后的系数直接求取能量熵或者AM调制作为特征[12]。

文中提出基于小波包基与能量熵的脑磁特征提取方法，将经主成分分解(PCA)法降维后的MEG数据进行小波包分解，结合小波熵概念从小波包库中选择最优小波包基，接着对最优基所对应的小波系数进行幅度调制求取能量熵，将能量熵的最大值、最小值、均值、方差构成特征向量作为SVM的输入，实现MEG信号的自动分类。

1 脑磁信号特征提取

1.1 最优小波包基

小波包分解(Wavelet Packet Decomposition,WPD)能够为信号提供更精细的分析方法。它将频带进行多层次划分，将多分辨率分析没有细分的高频部分进一步分解，并能够根据被分析信号的特征，自适应地选择相应频带，使之与信号频谱相匹配，从而提高了时频分辨率。

小波包变换的双尺度方程为:

(1)

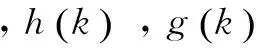
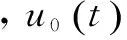
小波包系数的递推公式为：

(2)

在小波包分解中，对于给定的小波，长度为M=2N的信号可以分解为深度为N的完整二叉树。通常一棵完整的二叉树的子树数目较大，且并非所有的子树都有价值，所以就有了最佳小波包基的选择问题。1992年，Coifman等[13]提出了最佳基选择准则用于解决最优树的选择问题。该准则是在不改变二叉树为分解结构的基础上加入熵作为下一步分解的准则，具体是当一个节点对应的子空间中的小波包熵大于其下一级子节点对应的两个子空间的小波包熵之和时才继续划分，否则停止划分。小波包熵有五种常用的标准，即：香农(Shannon)熵、阈值熵、范数(norm)熵、对数能量(logenergy)熵、SURE熵[14]。文中使用对数能量熵，其定义为：

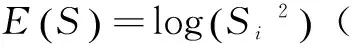
(3)

式中，S代表信号；Si代表信号S在一个正交小波包基上的投影系数。

1.2 幅度调制与能量熵

基于Hilbert变换的幅度调制方法(AM)能够准确地获得信号在采样频率上的包络，以及量化事件相关去同步化(Event-Related Desynchronization,ERD)[15]的活动。文献[10]将幅度调制与离散小波变换(Discrete Wavelet Transform,DWT)结合用于提取EEG的包络特征，对左手移动和静息状态的单务脑电信号的平均分类准确度为84.4%。基于Hilbert变换的幅度调制公式为：

(4)

式中，H(x)为对MEG信号x的Hilbert变换；Si为最优小波基的节点系数。

另外，相比于通道数较少的脑电信号，全头型脑磁图设备记录的脑磁信号的通道数较多。为了提高分类精度并减少特征提取的计算量，文中在对小波包系数进行幅度调制后计算调制包络的能量熵，对小波包系数幅度调制后计算能量熵可以表征信号复杂度在时域的变化情况，也可以表征信号的频域特征，具有良好的时域局部化能力[16]。由香农熵的定义[17]，时域能量熵可表示为：

(5)

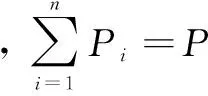
由式(5)可知：当时域能量在信号总能量中的比重大时，能量熵小；当时域能量在信号总能量中的比重小时，能量熵大。

1.3 基于小波包基与能量熵的特征提取方法

小波包分解将频带进行多层次划分，对多分辨率分析没有细分的高频部分进一步分解，自适应地选择相应频带，使之与信号频谱相匹配，从而提高了时频分辨率；基于Hilbert变换的幅度调制方法能够准确地获得信号在采样频率上的包络，以及量化事件相关去同步化的活动；而能量熵可以表征信号复杂度在时域的变化情况，也可以表征信号的诸多频域特征，具有良好的时域局部化能力。

文中结合小波包分解和能量熵的优点，提出了基于小波包基与能量熵的脑磁信号特征提取方法。利用该方法提取的特征值区分正常人和精神病分裂症患者的脑磁信号的分类精度可达97.586 8%。算法步骤为：

步骤1：选用小波包函数对预处理后的每一段脑磁数据进行小波包分解，得到完全分解树。

步骤2：对树中的每个节点Ni,j按照式(3)计算第i层的第j个节点的小波包熵Ei,j，运用最小小波熵的原则求取最优小波包基树。

步骤3：对最优小波包基树中的每一个节点按照式(2)求取其小波包系数，并对求取的每一个小波包系数按照式(4)进行AM调制。

步骤4：将AM调制后的数据分割成n段，按照式(5)求取能量熵。为了进一步降低特征维数，对每一组小波包系数对应的能量熵求取最大值﹑最小值﹑均值和方差等统计特性，作为提取的特征值。

将提取的每段MEG信号的特征值组成该组信号的特征向量，用该特征向量训练SVM分类器，从而实现对正常人和精神分裂症患者的MEG信号的分类。

1.4 SVM分类器

支持向量机是Cortes等[18]于1995年首先提出的，它在解决小样本、非线性及高维模式识别中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中。SVM方法是建立在统计学习理论的VC维理论和结构风险最小原理基础上的，通过构造一个超平面作为决策面将两类样本尽量正确分开且分离的两类间隙最大化，若样本是非线性的，可以映射到高维变为线性的，然后再进行分类。它的优点在于通过最大化网络的性能以及降低学习机的复杂度来平衡准确度。

(6)

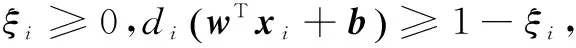
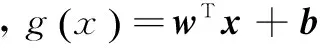
通过选取最优的w和b得到判决函数：

(7)

(8)

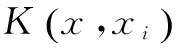
一般情况下，SVM选择的内核函数有多项式核函数或径向基函数(RBF)核函数：

(9)

(10)

其中，σ为宽度参数。

2 基于小波包基与能量熵的特征提取方法实验

2.1 数据和数据预处理

实验中使用的脑磁数据来源于美国NIH(National Institute mental Health)研究中心，脑磁数据采用具有275个通道的CTF-275脑磁测量仪采集[19]。实验采集了2个类别共18位测试者的脑磁信号，其中包括9位正常人(Normal)、9位精神分裂症病人(Patient)。测试者处于闭眼休静息状态，采样频率为600 Hz，采集时间为240 s。将采集到的MEG信号去除噪声和伪迹得到纯净的脑磁信号。为了减少计算量，实验中将数据降频到150 Hz，提取26 s到46 s的数据段进行分析，故每个数据样本都是一个275×3 000的二维数据阵列。

在进行特征提取前，先对数据进行信号异常点更正﹑MEG数据的降维以及MEG分段等预处理。首先进行异常点更正，将大于样本平均值195%的点或小于样本平均值5%的点分别用样本平均值×1.95及样本平均值×0.05替代。接着对多通道的MEG的数据运用PCA法对数据信息进行降维，去掉冗余信息，留下代表主要信息的分量，从而减少计算量[20]。设M道原始数据构成一个M×N的数据阵W(N表示每段数据的长度，N>M)，令WW'=V(W'为W的转置)，V为W的协方差阵，V可作如下分解：

(11)

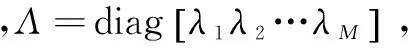
(12)

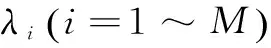
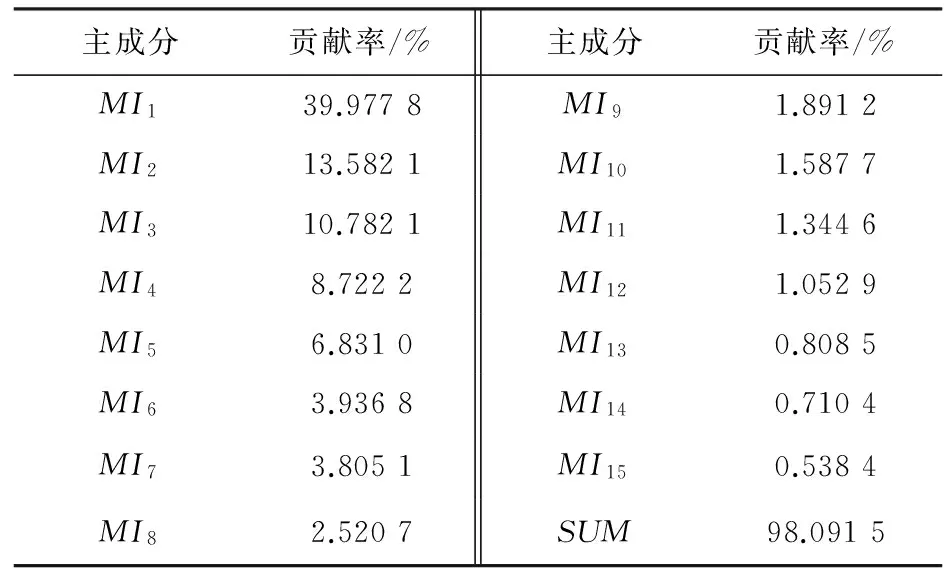
表1 贡献率

最后对降维后的15个主成分MEG信号用矩形窗进行分段[21]，每1 000个数据点分一段，下一段与上一段数据重叠500个点。这样每一个主成分20s的数据就被分为5段，每一位受试者的MEG数据共分为75段数据样本，每个样本的长度为1 000个数据点。

2.2 实验过程与结果分析

在特征提取中选用Db2小波函数对每一段MEG数据进行4层小波包分解，并根据对数能量熵准则选取最优小波包基。图1为对PCA降维后的一段脑磁信号小波包分解后的最优小波包基的选择结果。

图1 最优小波包基选择结果示意图

从图中可以看出，通过最优小波基的选取可以在不影响信息量的同时减少二叉树的节点数。

图2是对选择出的最优小波包基的小波包系数进行AM调制后的包络图。最后提取每个包络的能量熵，对能量熵求取统计特性，包括最大值﹑最小值﹑均值和方差。

图2 小波包系数进行AM调制的包络图

此外使用单因素分析方法对两类MEG数据提取的四维特征向量(能量熵的最大值、最小值、均值、方差)进行分析，表2是单因素分析的结果。

表2 单因素分析结果

从表中可以看出，按文中提出的方法从正常人(Normal)和精神分裂症病人(Patient)的两类脑磁信号中提取的特征值是有显著性差异的。为了进一步分析文中提取的正常人脑磁信号和精神分裂症病人脑磁信号的特征差异，分别分析了文中提取的正常人脑磁信号和精神分裂症病人脑磁信号的特征盒形图，如图3所示。从图中可以看出，两类样本是有明显差别的。

文中分别将能量熵的最大值、最小值、均值、方差组合成的4维特征向量作为SVM的输入。将预处理后的675个正常人脑磁数据和675个精神分裂症病人的脑磁数据随机等分为9个子集，进行0到1归一化操作后，从中分别选出8个子集作为训练样本，交叉验证求取SVM中的最优参数，剩余一组子集作为测试样本，以9次识别率的均值作为平均识别率。

图4给出了参数选择的结果图。

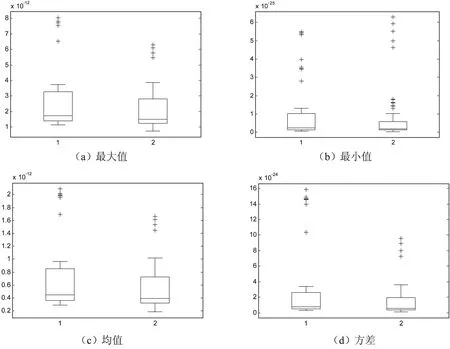
图3 正常人脑磁信号和精神分裂症病人脑磁信号的特征盒形图

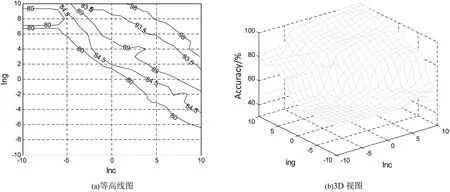
图4 SVM参数选择结果图

从图4可以看出，当参数c取1 024，g取32时，训练的正确率为100%，测试样本正确率为97.586 8%。

表3给出了基于文中的小波包基与能量熵的特征提取方法的分类结果与其他特征提取方法分类结果的比较。实验结果表明：文中提出的基于小波包基与能量熵的MEG自动分类方法的准确率较高，高于表中列出的现有方法。

表3 分类准确率对比

3 结束语

文中提出了一种新的脑磁特征提取与识别的方法。该方法从新的角度结合小波包分析，最优小波包基选取，以及对小波包系数的幅度调制，来提取正常人与精神病患者的脑磁特征。同时为了减少特征向量的维数，对幅度调制的包络求取能量熵来提取脑磁特征向量。文中考虑了个体的差异，针对每一个个体单独求取特征向量，在分类阶段通过交叉验证寻求最佳分类器参数。实验结果表明，基于小波包基与能量熵的MEG自动分类方法有较高的分类准确度，分类准确率可达97.586 8%。

[1] 李 坤,褚蕾蕾,朱世东,等.基于mu节律能量的运动意识分类研究[J].计算机技术与发展,2006,16(8):157-159.

[2] 罗志增,李亚飞,孟 明,等.脑电信号的混沌分析和小波包变换特征提取算法[J].仪器仪表学报,2011,32(1):33-39.

[3] 文 念,黄丽亚,于 涵,等.基于ICA和聚类的EEG脑源定位研究[J].计算机技术与发展,2015,25(5):228-232.

[4]ZhukovL,WeinsteinD,JohnsonC.IndependentcomponentanalysisforEEGsourcelocalization[J].IEEEEngineeringinMedicineandBiologyMagazine,2000,19(3):87-96.

[5] 侯凤贞,戴加飞,刘新峰,等.基于网络连接度指标的脑梗死患者脑电信号相同步分析[J].物理学报,2014,63(4):59-64.

[6]HuberleE,LutzenbergerW.Temporalpropertiesofshapeprocessingbyevent-relatedMEGadaptation[J].NeuroImage,2013,67:119-126.

[7]CravoAM,RohenkohlG,WyartV,etal.Temporalexpectationenhancescontrastsensitivitybyphaseentrainmentoflow-frequencyoscillationsinvisualcortex[J].TheJournalofNeuroscience,2013,33(9):4002-4010.

[8]MirzaeiA,AyatollahiA,GifaniP,etal.EEGanalysisbasedonwavelet-spectralentropyforepilepticseizuresdetection[C]//Procof3rdinternationalconferenceonbiomedicalengineeringandinformatics.[s.l.]:IEEE,2010:878-882.

[9] 王 登,苗夺谦,王睿智.一种新的基于小波包分解的EEG特征抽取与识别方法研究[J].电子学报,2013,41(1):193-198.

[10] 王 攀,沈继忠,施锦河.基于小波变换和时域能量熵的P300特征提取算法[J].仪器仪表学报,2011,32(6):1284-1289.

[11]KremerJ,PedersenKS,IgelC.Activelearningwithsupportvectormachines[J].WileyInterdisciplinaryReviewsDataMining&KnowledgeDiscovery,2014,4(4):313-326.

[12]HsuWY,LinCH,HsuHJ,etal.Wavelet-basedenvelopefeatureswithautomaticEOGartifactremoval:applicationtosingle-trialEEGdata[J].ExpertSystemswithApplications,2012,39(3):2743-2749.

[13]CoifmanRR,WickerhauserMV.Entropy-basedalgorithmsforbestbasisselection[J].IEEETransactionsonInformationTheory,1992,38(2):713-718.

[14] 张德丰.MATLAB小波分析[M].北京:机械工业出版社,2009:158-163.

[15]ClochonP,FontbonneJM,LebrunN,etal.AnewmethodforquantifyingEEGevent-relateddesynchronization:amplitudeenvelopeanalysis[J].ElectroencephalographyandClinicalNeurophysiology,1996,98(2):126-129.

[16] 胡剑锋,穆振东,肖 丹.基于能量熵的运动想象脑电信号分类[J].计算机工程与应用,2008,44(33):235-238.

[17] 陈 悦,张少白.LM算法在神经网络脑电信号分类中的研究[J].计算机技术与发展,2013,23(2):119-122.

[18]CortesC,VapnikV.Support-vectornetworks[J].MachineLearning,1995,20(3):273-297.

[19]ZhangXJ,WangYT,WangYJ,etal.Ultra-slowfrequencybandsreflectingpotentialcoherencebetweenneocorticalbrainregions[J].Neuroscience,2015,289:71-84.

[20]LinCT,WangYK,ChenSA.AnEEG-basedbrain-computerinterfacefordualtaskdrivingdetection[C]//Procofneuralinformationprocessing.Berlin:Springer,2011:701-708.

[21]NakayamaK,KanedaY,HiranoA.AbraincomputerinterfacebasedonFFTandmultilayerneuralnetwork-featureextractionandgeneralization[C]//ProcofISPACS.Xiamen:IEEE,2008:826-829.

Automatic Classification Method of MEG Based on Wavelet Packet and Energy Entropy

ZHANG Xue-jun1,2,DING Yu-han1,HUANG Li-ya1,2,CHENG Xie-feng1,2

MEG signals associated with many physiological information related to mental illness is an important basis for judging abnormal nervous system activity and has great significance for the study of brain science.In order to improve accuracy of normal and schizophrenia’s MEG signals,a new method of MEG classification with feature extraction is proposed based on wavelet packet and energy entropy.First,it reduces the dimension of the raw signals by Principal Component Analysis (PCA) and decomposes preprocessed signal by Wavelet Packet Decomposition (WPD).Then,selects the best basis of wavelet packets from a wavelet packet library according to the wavelet packet entropy,afterwards calculating the energy entropy of envelope that acquired by Amplitude Modulation (AM) of the best basis wavelet coefficients.Moreover,the eigenvector is obtained by calculating the statistical features of energy entropy.Finally,the feature vectors are put into a Support Vector Machine (SVM) to realize automatic classification of MEG.Experiment shows that the proposed method could achieve a great classification accuracy of 97.586 8%,which indicates that the feature extraction method in this paper can effectively extract the characteristic of MEG and improve the classification accuracy.It provides evidence for the treatment and severity assessment of schizophrenia.

MEG;wavelet packet decomposition;amplitude modulation;energy entropy;support vector machine

2015-08-25

2015-12-03

时间：2016-06-00

国家自然科学基金资助项目(61271334)

张学军(1969-),男，博士,教授,研究方向为智能信息处理、认知网络频谱感知、无线射频识别技术等；丁钰涵(1992-)，女，硕士研究生，研究方向为智能信息处理。

R318

A

1673-629X(2016)06-0127-06

10.3969/j.issn.1673-629X.2016.06.028

(1.School of Electronic Science and Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China;2.Jiangsu Province Engineering Lab of RF Integration & Micropackage,Nanjing 210003,China)