基于最小生成树的规则图像碎片复原算法

赵 林，朱桂斌，文玉强，戚 曹

(1.重庆通信学院 应急通信重庆市重点实验室，重庆 400035;2.重庆通信学院 信息资源管理应用教研室，重庆 400035)

基于最小生成树的规则图像碎片复原算法

赵 林1，朱桂斌2，文玉强1，戚 曹1

(1.重庆通信学院 应急通信重庆市重点实验室，重庆 400035;2.重庆通信学院 信息资源管理应用教研室，重庆 400035)

文中针对大数量的规则图像碎片进行了拼接复原研究，在图像碎片缺少外形轮廓这一匹配特征和碎片数量庞大的前提下，提出了一种基于最小生成树原理的规则图像碎片快速复原算法。通过计算图像碎片边缘像素差异值的方法对碎片进行匹配，再运用贪心策略的思想，通过最小生成树原理对图像进行复原框架设计，完成了对规则图像碎片的快速复原。而且相比现有算法，文中算法无需知道原始图像的尺寸，更为符合实际应用情况。仿真结果表明，文中算法完成了对大数量图像碎片的复原工作，具有快速、准确的特点。

规则碎片；匹配；复原；最小生成树

1 概 述

如今，随着计算机等硬件设备的不断发展，通过数字图像输入设备来获得更加清晰的数字图像已不成问题。利用扫描仪或者数码相机获取图像碎片的数字图像，之后利用碎片的颜色、形状等信息探测出相邻的碎片，进而让计算机程序自动拼接相邻碎片，最终实现图像的复原。这类问题广泛存在于情报和密码破译、图像信息修复及司法物证复原等方面，特别是当碎片数量巨大，人工拼接难以在短时间内完成任务时，我们就可以借助现代计算机技术从成千上万图像碎片中找到互相邻接的图像碎片，通过相应算法计算并最终拼接成完整的图像[1]。此应用是计算机视觉、模式识别等领域中的一个新颖且典型的应用，也引起了国内外学者的广泛关注。近年来，很多学者纷纷开展研究并提出了很多行之有效的方法。至此，图像碎片的自动拼接成为了计算机应用领域的一个研究热点，也是一个难点。

常规图像碎片拼接方法主要研究非规则碎片的匹配，利用碎片边缘的尖角、尖点、面积及轮廓等特征，搜索与之匹配的相邻碎片进行拼接，但对于有些外形无区别的矩形图片碎片来说，例如碎纸机破碎文档所形成的矩形碎片，它缺少了每个碎块所特有的重要匹配特征——形状，处理这种类型的碎片具有相对较大的挑战，所以利用非规则碎片的拼接技术显然不合理。所以对于外形相同的规则图像碎片的复原来说，就要关注其图像内容来解决匹配方面的问题。例如在文献[2]中，作者采用了估计碎片匹配对边缘值的方法来进行匹配，而这种方案最终恢复了一幅共有3 300块碎片的图像，这也是处理规则图像碎片匹配方面的又一创新。

对于规则图像碎片的复原，研究的核心有两点：

一是如何在碎片间进行匹配，采用何种方法来计算它们之间的匹配度；

二是采取何种复原结构来快速无误地复原出原始图像。

在碎片匹配方面，Kosiba在文献[3]中首次利用了碎块形状和图像内容信息来匹配碎片，提出了在碎片的轮廓边缘上计算两侧像素差值的方法，依计算出的差值来判决碎片是否相邻，随后在文献[4-5]中也采取了类似的匹配计算方法，并且在文献[4]中详细证明了此方法具有高效的匹配性和较低的计算开销，是一种简单有效的方法，也是在规则碎片匹配中广泛应用的方法。

在图像碎片复原方面，目前有采取动态规划[5]、匈牙利方法[6]和贪婪算法[4]的解决方案，它们都是现今主流的计算机处理方法，但它们之中存在的问题主要有可处理的碎片数量较少、复原度不高和需要过多的限制条件。

所以，基于现今存在的问题，在提高处理数量的同时不失准确度这一原则下，文中提出了基于最小生成树的规则图像复原方法。对来自同一幅图像的n个互不重叠的无方向变换的正方形图像碎片，在无需其他原始图像先验信息的条件下，运用文中提出的复原方案可以快速完成碎片间的匹配并恢复出复原率较高的原始图像。

在匹配计算方面，文中采用了基于边缘色彩差异值的算法，此算法不仅可以有效匹配相邻碎片，同时还有较小的计算代价。而在复原构架的设计上，文中在参考了文献[2-3，5-7]的基础上，基于最小生成树原理设计了复原结构。相对于文献[2-3]所采用的基于贪婪算法的复原方案，文中方法能更快地复原出原始图像，同时具有简便的算法结构和较高的复原度，而在计算代价上相对现存算法有较小的计算开销[8]。

通过仿真实验结果显示，文中算法具有良好的复原效果。

2 基于边缘色彩差异值的图像碎片匹配

在匹配过程中采用边缘色彩差异度的匹配算法，这种算法具有更广的适配性，在文献[4]中被证明是最为高效的匹配算法。对于规则碎片的匹配，只需考虑碎片边缘的颜色匹配问题。若是在原始图像中两碎片相邻，则它们在相邻边缘上会有相似的色彩分布，则在相邻边缘上，两个碎片间的差异值和最小，以此作为评判标准来计算它们之间的匹配度。

对于彩色图片，可取R,G,B色彩空间的矢量进行匹配计算，通过计算碎片间的匹配度大小来判断它们在原始图像中是否邻接。用D代表碎片对之间的匹配度，对于碎片xi和xj，设定它们之间的空间关系为R∈{u,r,d,l}，u,r,d,l分别代表碎片xj位于xi的上、右、下、左侧，用D(xi,xj,R)表示碎片xj位于碎片xi相应位置的匹配度。编号为i和j的碎片左右边缘匹配程度(i左j右)用相同位置(m表示对应的行数)的灰度差的积累结果衡量，定义边缘匹配函数为公式(1)。此值越小，说明匹配程度越好，吻合程度越好。

(1)

首先把一幅原始图像分解为N幅碎片图像并且进行无方向变化的随机置乱，每个碎片大小为P*P。假设有待匹配碎片xi和xj，为每个碎片分配P*P*3大小的矩阵。当碎片位于左侧时，用D来表示这两个碎片之间的匹配度，其值越小，则两个碎片之间的匹配度越高，如式(2)所示。

D(xi,xj,l)=

(2)

显然，两个碎片相邻的可能性越大时，匹配度D就会越小。把每块碎片与剩余的碎片依次做匹配计算，之后把求得的值放入碎片匹配值矩阵D(xi,xj,r)中，它的大小为N*N*4。因为匹配涉及的碎片没有进行方向变换，所以第一层矩阵放入的是碎片xi第一边和碎片xj第三边的匹配值，第二层矩阵放入的是碎片xi第二边和碎片xj第四边的匹配值，第三层矩阵放入的是碎片xi第三边和碎片xj第一边的匹配值，第四层矩阵放入的是碎片xi第四边和碎片xj第二边的匹配值。

3 基于最小生成树的图像碎片复原

针对规则图像碎片，文中在碎片的复原过程中运用图论学中的最小生成树原理[9]。它是一种运用了“贪心”策略的最优化解决方法[10]，运用到碎片复原中可以看出，复原图像初始时从一个碎片开始逐步加入其余碎片直到全部拼接完毕。而且不需要知道原始图像的其他先验知识，如原始图像的尺寸，也无需人工干预。

3.1 最小生成树原理

根据文献[11-12]所提出的克鲁斯卡尔(Kruskal)算法,来寻找复原图像相应的最小生成树。设图用G=(VG,EG)表示，其中VG和EG分别表示图G的节点集合和边集合，也就是把节点集和边集作为图的属性来表示。节点就是每个图像碎片，而边就是碎片之间的连接关系，其中每一个节点u∈VG可以指向满足条件(u,v)∈EG的节点v，EG的元素一般用(u,v)表示，其中u,v属于VG，而边的权重为矩阵D(xi,xj,r)中存放的碎片之间的匹配值D。

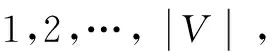
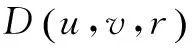
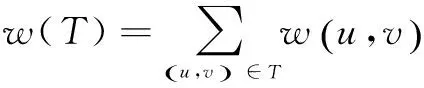
(3)

因为T无回路且连接了所有节点，所以它必然是一棵树，故称之为最小生成树[14]。

3.2 基于最小生成树的图像碎片复原算法

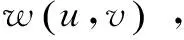
在此阶段，根据Kruskal算法的思想，从图中寻找其最小生成树来构造复原图像。在起始阶段，把每一个节点(碎片)当作一棵树，也就是令最小生成树的初始状态为只有N个节点而无边的非连通图T=(VG,{})，根据边集合以及它们每条边所对应的权重找到最低代价(最高匹配度)的边emin并且从边集合中取出，若是属于这个边emin的节点(碎片)属于同一棵树，则舍去这条边，若是不属于同一棵树，则把具有最小权值的边emin作为安全边，并把它添加到正在生长的树中。在添加过程中，若是分别属于两棵树中的节点(碎片)占用了同一个位置，则舍去这条边。算法伪代码如图1所示。

图1 算法伪代码

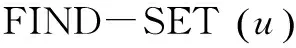
接下来对一幅图像碎片进行复原。图2显示的是一幅像素数为800*600的图像及其任意置乱的碎片，碎片的边长像素数为40，数量为300块。

图2 原始图像及其置乱图像

对图2中的置乱图像，采取文中提出的复原算法对其进行复原。初始每个碎片都是一棵含有一个节点的树，把匹配值D最小(权重值w最大)的两个碎片作为复原起点，按照算法的约束条件依次加入合法的碎片，直到碎片全部加入并形成一棵树，最终按照生成树中的位置信息复原出图像。复原过程如图3所示。

图3 碎片图像复原过程

4 仿真结果及分析

在算法仿真过程中，采取中文算法和文献[4]的算法对碎片图像进行复原仿真并作出比较。文中使用CPU为2.20GHzIntel(R)Core(TM)T6670的计算机在MatlabR2013a的仿真平台上进行编程实验。

选定三种尺寸的20幅图像，把碎片边长设定为50*50，对其打乱，分别包含有400块、800块和1 200块碎片。对每幅图像碎片运用文中算法测试10次，记录其复原的最高准确度、最低准确度和平均准确度，如表1所示。

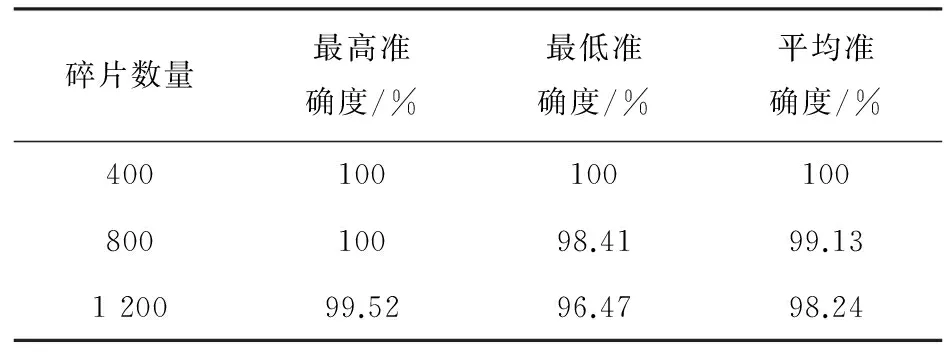
表1 文中算法运算性能分析

对文中算法和文献[4]中提出的算法进行比较，对上述20图像进行测试，每幅图像碎片测试10次，对每次运行结果取最高准确值作比较，如表2所示。

表2 算法性能比较

由表2可知，文中算法相对文献[4]算法具有较高的复原准确度。

为了能直观地说明文中算法复原的有效性和优越性，选取文献[4]中所提供的2幅图像，分别对其置乱，然后应用文献[4]的算法与文中算法进行比较，其结果如图4所示。图中，第一行为置乱图像，第二行为文献[4]算法所复原的图像，第三行为文中算法所得图像。

图4 比较结果

由图4可知，采取文中算法处理的碎片图像，复原的准确度得到了大幅提升。由于文中算法采用了贪心策略，在复原过程中无需知道原始图像尺寸，这也是文中算法的独特之处，较以往算法更为贴合实际应用。

5 结束语

文中提出了一种用于规则图像碎片的快速复原算法。在算法实现中，运用了文献[4]提出的基于边缘色彩差异度的匹配算法，同时结合了图论学中的最小生成树原理用于复原框架的设计。由仿真实验可知，文中算法对于大量规则图像碎片可以进行准确复原，同时相比文献[4]算法，准确度有了大幅度提升。在下一步的工作中，会根据实际应用的需求，在匹配过程中，对存在照度突变或噪声干扰的情况下如何对碎片精确匹配进行研究。同时，对方向错乱的图像碎片复原进行研究并进行算法实现。

[1] 先 毅.图像碎片复原方法的研究[D].北京：华北电力大学,2010.

[2]PomeranzD,ShemeshM,Ben-ShaharO.Afullyautomatedgreedysquarejigsawpuzzlesolver[C]//Proceedingsof

CVPR.Piscataway,NJ:IEEE,2011:9-16.

[3] Kosiba D A,Devaux P M,Balasubramanian S,et al.An automatic jigsaw puzzle solver[C]//Proceedings of the 12th International conference on image processing.Piscataway,NJ:IEEE,1994:616-618.

[4] Cho T S,Avidan S,Freeman W T.A probabilistic image jigsaw puzzle solver[C]//Proceedings of CVPR.Piscataway,NJ:IEEE,2010:183-190.

[5] Yang X,Adluru N,Latecki L J.Particle filter with state permutations for solving image jigsaw puzzles[C]//Proceedings of CVPR.Piscataway,NJ:IEEE,2011:2873-2880.

[6] Alajlan N.Solving square jigsaw puzzles using dynamic programming and the hungarian procedure[J].American Journal of Applied Sciences,2009,5(11):1941-1947.

[7] Sholomon D,David O,Netanyahu N S.A genetic algorithm-based solver for very large jigsaw puzzles[C]//Proceedings of CVPR.Piscataway,NJ:IEEE,2013:1767-1774.

[8] Toyama F,Fujiki Y,Shoji K,et al.Assembly of puzzles using a genetic algorithm[C]//Proceedings of CVPR.Piscataway,NJ:IEEE,2002.

[9] Held M,Karp R M.The traveling-salesman problem and minimum spanning trees:Part II[J].Mathematical Programming,1971,1(1):6-25.

[10] 朱 青.计算机算法与程序设计[M].北京：清华大学出版社,2009:122-126.

[11] Kruskal J B.On the shortest spanning subtree of a graph and the travelling salesman problem[J].Proceedings of the American Mathematical Society,1956,7:48-50.

[12] Cormen T H,Leiserson C E,Rivest R L,et al.Introduction to algorithms[M].2nd ed.[s.l.]:McGraw-Hill,2001:1297-1305.

[13] 朱清新，杨 凡，钟黔川.计算机算法设计与分析导论[M].北京:人民邮电出版社,2008.

[14] Matsui T. The minimum spanning tree problem on a planar graph[J].Discrete Applied Mathematics,1995,58(1):91-94.

A Restoration Algorithm for Square Image Pieces Based on MST

ZHAO Lin1，ZHU Gui-bin2，WEN Yu-qiang1，QI Cao1

(1.Chongqing Key Laboratory of Emergency Communication,Chongqing Communication Institute,Chongqing 400035,China;2.Teaching and Research Section of Information Resources Management and Application,ChongqingCommunication Institute,Chongqing 400035,China)

The matching and restoration for large number of square image pieces are studied in this paper.On the premise of lacking outline and large quantity of pieces,a fast restoration algorithm for square image pieces based on Minimum Spanning Tree (MST) is put forward.It calculates the difference of pixel value on the edge to match two pieces,then with the idea of the greedy strategy,the structure for restoration of square image pieces is designed,completing the quick restoration of square image pieces finally.Compared with the existing algorithms,this algorithm does not need to know the size of the original image,more accorded with the actual application situation.Simulation indicates that it can complete the restoration for tens of thousands pieces rapidly and accurately.

square pieces;matching;restoration;minimum spanning tree

2015-08-31

2015-12-09

时间：2016-06-00

国家自然科学基金资助项目(61272043)；重庆市基础与前沿研究重点项目(cstc2013jjB40009)；重庆科技研发基地能力提升项目(cstc2014pt-sy40003)

赵 林(1990-)，男，硕士研究生，研究方向为图像与视频分析；朱桂斌，教授，博士，研究方向为信息安全、图像处理。

TP391

A

1673-629X(2016)06-0069-05

10.3969/j.issn.1673-629X.2016.06.015