基于SIR社交网络中商业谣言传播研究
2016-02-27余莎莎王友国
余莎莎,王友国,朱 亮
(1.南京邮电大学 理学院,江苏 南京 210046;2.南京邮电大学 通信与信息工程学院,江苏 南京 210003)
基于SIR社交网络中商业谣言传播研究
余莎莎1,王友国1,朱 亮2
(1.南京邮电大学 理学院,江苏 南京 210046;2.南京邮电大学 通信与信息工程学院,江苏 南京 210003)
研究了社交网络中信息传播机制并建立了数学模型模拟传播过程。通过分析信息在社交网络中的传播特点,结合传播动力学中的羊群效应及信息老化效应,以经典的SIR传染病模型为基础,建立了符合在线社交网络中谣言传播特性的信息传播模型,对网络中的各状态人数变化趋势进行数值仿真。最后分析了网络中一类谣言传播及雇佣网络推手进行辟谣对谣言传播动力学的影响。实验结果表明,在最佳时间点雇佣网络推手进行辟谣,经济损失减至最小,并且能有效抑制谣言传播。为相关职能部门在舆情监控决策方案上提供了理论分析。
社交网络;传染病模型;羊群效应;信息老化效应;商业谣言
0 引 言
在线社交网络(Online Social Network,OSN)[1-3]是一个以数据为中心的网络,源于六度分割理论[4]和150度法则,允许人们自由创作、交流内容并进行一系列社交互动活动,是当前网络社会实践活动的集中体现,例如Facebook[5]、Twitter[6]和新浪微博[7]等。用户在社交平台浏览信息,通过转发或分享等方式就能传播信息并且传播迅速、难以控制,甚至无法辨别对错,世界经济论坛称之为“网络谣言”并强调了其威胁性[8-9]。
随着经济全球化的发展,网络谣言与经济活动的联系也越发密切,谣言的滋生越来越多是出于商业利益驱动。借助社交网络这一新媒体形式,散布网络谣言诋毁竞争对手更是被当成一种竞争手段。例如,2008年肯德基“怪鸡”事件,后来证明是无稽之谈,但却造成企业股票下跌、人事变动,损害了企业声誉。因此,研究在线社交网络中谣言传播现象具有现实意义。Allport等最先研究了谣言心理学,揭示了“生理心理系统”对社会的促进作用[10];Java指出信息在虚拟社区中的传播过程服从某种规律[11];Alison等发现网络环境中谣言的传播与传染病传播具有相似性,可以用传染病模型作为描述这种现象的一种方法[12];Wang等在平均场模型的基础上研究了传染病模型,如基于SI,SIR和SIS的改进模型等[13-14]。这些研究对谣言在社交网络中的传播规律进行了很有意义的挖掘与探讨。文中基于网络谣言数据生命周期的特点,根据Kermack与McKendrick建立的经典的SIR模型[15],将网络谣言传播过程中对应用户状态划分为易感者(Susceptible individual)、传播者(Infected individual)和免疫者(Recovered individual),建立在线社交网络谣言传播模型。
文中关注社交网络中谣言传播动力学问题并将其应用到商业中的负面谣言处理。在经典SIR模型基础上考虑信息传播过程中的羊群效应[16]及信息老化效应[17],研究了谣言传播的动力学特征。并通过数值仿真,研究谣言扩散造成的经济损失以及雇佣网络推手控制谣言传播带来的收益。
1 理论模型
以社交网络为背景的经典SIR模型通常基于以下假设:
(1)社交网络是一个相对稳定的系统,网络中的用户总人数基本保持一个定值。
(2)易感者与传播者的接触(即社交网络中的关注)接收信息,并以一定的概率选择传播信息或者只阅读。在以t时刻为起点的某单位时间内,单个传播者所能感染的易感人数与t时易感人群总人数成比例,比例系数为λ1。
(3)在以t时刻为起点的某单位时间内,传播者以一定的概率转化成免疫者,转化概率为μ。
在以上三种假设下,得到的传染病模型如下:
(1)
其中,S(t),I(t),R(t)分别表示易感者、传播者、免疫者在总人群中所占的比例;S0,I0,R0表示初始状态下各状态人数初值,且均为非负数。
2018年5月17日俄罗斯国家杜马立法工作委员会正式审议通过了将数字经济的基本条例添加到俄罗斯联邦民法典中的提案。
描述了信息传播过程中被感染者在治愈后具有免疫力,因而成为免疫者并且不会再次被感染,从而移出传播系统不再感染其他用户。但是考虑存在易感者在接触谣言之前接受了辟谣消息,从而以一定的比例直接转化成免疫者,比例系数为λ2。考虑该情况后,将式(1)改进为:
(2)
其中,λ1为易感者转化为感染者的比例系数;λ2为易感者直接转化为免疫者的比例系数。
经典的传播模型并没有刻画出谣言在社交网络中传播所固有的特性。网络用户心理直接或间接受他人影响而发生的一致行动对谣言的传播速度、传播规模都会产生影响。例如2011年日本大地震期间,谣言在Twitter平台上疯传[18];出现核泄漏危机后,国内沿海地区出现的抢盐风暴等[19]。在这个过程中由部分用户通过微博等社交平台发布或分享谣言信息,其他用户在获取先行动者的行动所传递的信息之后往往忽略个人意志采取相似的行动,避免可能的风险给自己造成的损失,这就是经济学中的羊群效应。Bikhchandani和Welch[20]最早提出信息学习模型来解释羊群效应,常用来分析为什么错误的决策不断被行为主体采纳并发现主体的一致行动就是一种信息缺损的过程。通常用Weibull分布密度函数[21]来描述这种现象,函数表达式为:
f(t)=θβtβ-1e-θtβ(θ>0,β>1)
(3)
其中,t为时间变量;θ为尺度参数;β为形状参数。
在式(2)中,易感者以恒定的概率转变成一个感染者,但在实际情况中,用户状态的转变往往是一个动态变化的过程。文中考虑到信息传播过程中羊群效应影响的谣言传播率变化中的时间变量,不妨将谣言传播概率视为随时间变化的函数并利用Weibull分布密度函数加以描述[22-23],这样更符合实际情况中的谣言传播规律。查阅文献[24],发现将传播概率函数通过设置不同参数与传播率为常数的谣言传播规律比较所得出的结论是一致的,不失一般性取θ=0.5,β=2,代入式(3)得:
f(t)=te-0.5t2
(4)
此外,谣言在传播过程中,自身的影响力及演化过程也随时间不断变化,一般而言,谣言影响力随着时间的推移而减小,谣言由于其热度的下降,在网络中渐渐消失,这就是网络谣言的信息老化现象。当用户对网络信息需求旺盛时,该信息的利用就多,其扩散也快;反之,当用户对信息需求程度越来越小时,对信息的利用就逐渐减少,其扩散速度也就越来越慢,此时信息出现老化趋势。文中在文献[25-26]的基础上,引用信息计量学中的经典理论—文献老化理论,在一定合理性的基础上应用至网络信息领域,并采用负指数模型[27]来衡量谣言发布后一定时间步长内的谣言影响力,具体的函数表达式为:
g(t)=e-δ(t-t0)
(5)
其中,g(t)为谣言的时效性影响力函数;δ为特征标度因子,用于描述谣言“三分钟热度”的时效性机理;t0为谣言在网站上发布的时刻。
由此,得到改进后基于传染病模型的谣言传播模型:
(6)
信息时代,商业谣言无障碍地发布、传递和共享的实现,无节制增加的公众数量都扩大了企业危机公关接受面,给品牌形象造成了巨大损害,甚至影响整个行业的安危[28]。对于负面商业谣言,企业除了网络公关部门进行辟谣以外,雇佣网络推手,发布辟谣信息已成为控制谣言扩散、减小企业损失的有效手段。对于在式(6)中给出的谣言传播模型,文中假定t=t'时刻,网络中感染者人数I(t')>φ(其中φ为感染者人数阈值),企业认为此时需要雇佣网络推手对网络谣言进行遏制,以减小谣言带来的损失。假设雇佣的网络推手人数为K,雇佣工作时间长为T,则考虑t'时刻后雇佣网络推手的谣言传播模型为:
(7)
2 模拟仿真
图1描述了企业对谣言传播未采取任何措施时,社交网络中各状态用户人数比例随时间变化的情况。由图1易发现,在谣言发布后,感染者人数比例不断上升,并且在t=0.872 5时刻达到峰值0.535 9,此后谣言传播者人数下降,最终消失。而易感者与免疫者人数比例则分别呈现单调下降与上升趋势,其变化速度先增后减,与感染者人数比例相关。
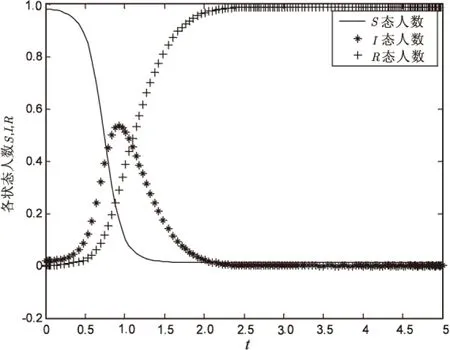
图1 企业未采取辟谣措施时各状态人数比例随时间变化图
图2描述了企业从初始时刻即雇佣网络推手进行辟谣时谣言在网络中的传播过程。通过观察图2发现,雇佣网络推手后,谣言扩散规模显著下降,易感者与免疫者的人数走势与图1相似,但其变化速度则出现了明显变化,这是由于谣言传播者的人数变化所造成的。
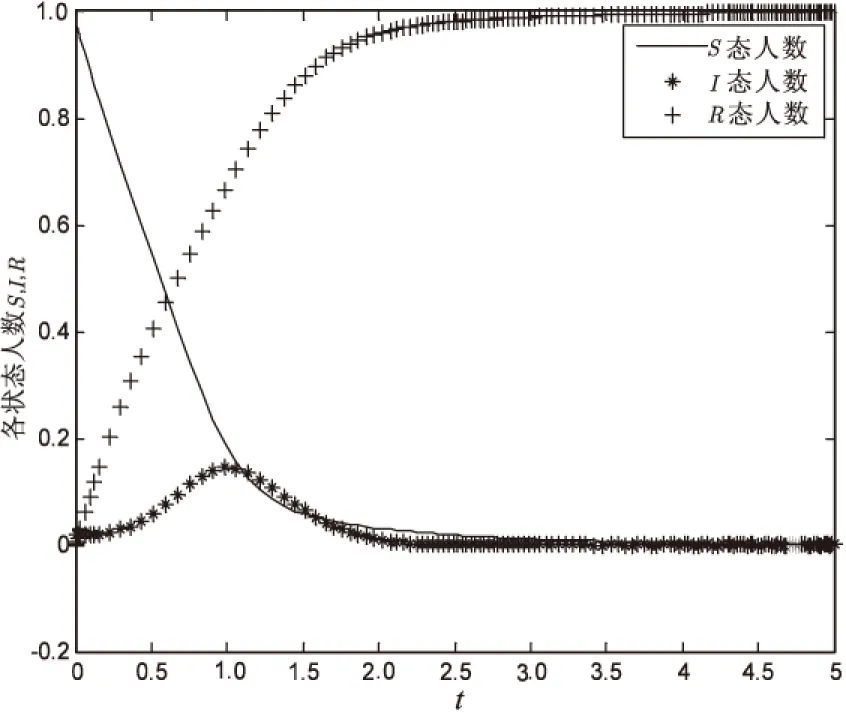
图2 企业雇佣网络推手辟谣时各状态人数比例随时间变化图
为进一步研究雇佣网络推手对谣言传播的影响,通过图3进行分析。由图3可知,雇佣网络推手后,谣言传播的峰值下降,感染者人数的变化速度减慢,但是谣言并未迅速消失,这是由于感染者人数减小后,其转化为免疫者的速度也相应减小,在长时间内感染者人数比例将保持缓慢减小并不断趋于零的状态。
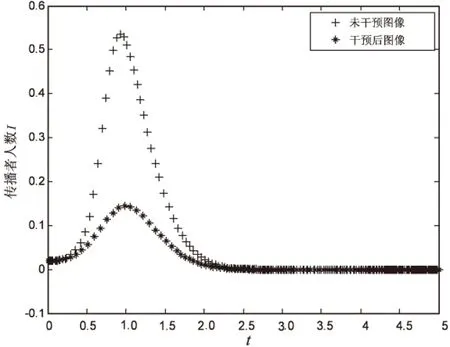
图3 企业雇佣网络推手辟谣前后感染态人数比例随时间变化图
3 讨 论
雇佣网络推手能够显著减小谣言传播带来的损失,但是由于谣言的潜伏性,很难从谣言发布时刻起就立刻雇佣网络推手进行遏制,同时,长时间雇佣网络推手也将花费较大的成本。因此,企业需要考虑在谣言传播过程中选择最佳时间点雇佣网络推手将经济损失与雇佣成本降到最低。假定单位时间内单个用户传播谣言造成的经济损失为C,则企业放任网络谣言扩散不采取任何措施,直至谣言老化最终消失而造成的总经济损失为:
(8)
其中,假定谣言在t=0时刻发布,t=T'时刻消失。
若在t'时刻,企业雇佣了K个网络推手且雇佣时长为T,假定单位时间内雇佣一个网络推手所需支付的成本与时间满足负指数关系e-10t,则此时网络谣言传播造成的损失及雇佣成本为:
企业雇佣网络推手花费的成本为:
m3(t)=TKe-10t
(10)
得到企业辟谣总经济损失并以此作为目标函数:
(11)
约束条件为:
(12)
其中,φ为谣言消失的观测指标,由于谣言在网络中彻底消失即感染者人数为零需要大量的时间,文中假定感染者人数比例I(t)≤5×10-5时,谣言即在网络中基本消失,此时不再需要雇佣网络推手。在目标函数M(t)中,不失一般性假设C=6 000,K=300(根据不同的网络及谣言传播情况,可设定相应变化的数值)。由图4可知,经济损失随干预时刻的增长先减后增,在t=0.375时,经济损失最小为52.410 4,此时雇佣网络推手的收益最大,总成本最小。并且由图5易知,传播者人数比较雇佣网络推手干预之前明显减少,即谣言在网络中的扩散速度减缓,破坏性降低。
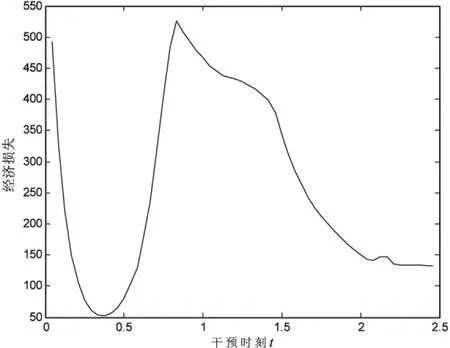
图4 企业经济损失随干预时刻变化情况
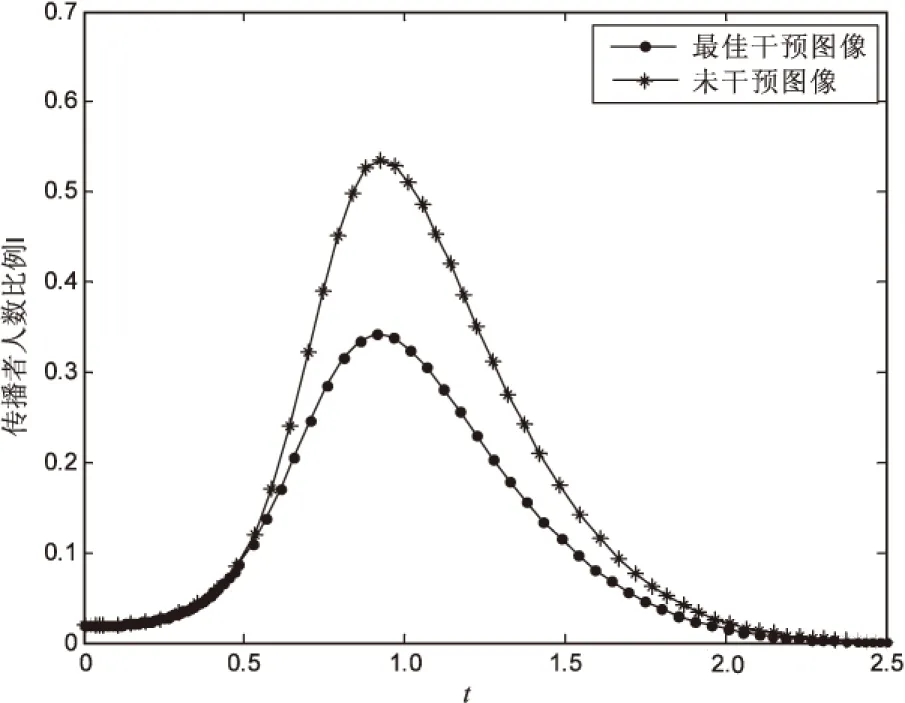
图5 最佳干预前后传播者人数比例随时间变化情况
4 结束语
文中根据经典的SIR传染病模型及真实在线社交网络中谣言传播的特点,提出一个改进的在线社交网络中商业谣言传播模型。首先通过建立基于SIR模型的动力学演化方程组,给出一个既能抑制谣言传播又能减少企业经济损失的策略——雇佣网络推手辟谣策略。然后对雇佣网络推手干预前后在线社交网络中商业谣言传播过程进行仿真,得到干预前谣言在社交网络中最大约有53.6%传播者的结论。雇佣网络推手策略利用网络推手本身的优势,对网络用户进行目标免疫,有效降低了谣言传播影响。
仿真结果表明:该模型能基本符合在线社交网络的传播特征。通过提取单位时间内单个用户传播谣言造成的经济损失及企业雇佣网络推手人数,模型能预估网络推手辟谣的最佳干预时刻,使得企业经济损失减至最小。事实上,真实在线社交网络的拓扑结构更为复杂,如随机性和社会性等。因此提出针对不同的网络拓扑结构特性的谣言免疫策略是今后的研究方向。
[1]Vega-RedondoF.Complexsocialnetworks[M].Cambridge:CambridgeUniversityPress,2007.
[2]SteinfieldC,EllisonNB,LampeC.Socialcapital,self-esteem,anduseofonlinesocialnetworksites:alongitudinalanalysis[J].JournalofAppliedDevelopmentalPsychology,2008,29(6):434-445.
[3] 熊澄宇,张 铮.在线社交网络的社会属性[J].新闻大学,2012(3):1-6.
[4]TraversJ,MilgramS.Anexperimentalstudyofthesmallworldproblem[J].Sociometry,1969,32(4):425-443.
[5]AcquistiA,GrossR.Imaginedcommunities:awareness,informationsharing,andprivacyontheFacebook[C]//Privacyenhancingtechnologies.Berlin:Springer,2006:36-58.
[6]KwakH,LeeC,ParkH,etal.WhatisTwitter,asocialnetworkoranewsmedia?[C]//Proceedingsofthe19thinternationalconferenceonworldwideweb.[s.l.]:ACM,2010:591-600.
[7] 孟 波.新浪微博:一场正在发生的信息传播变革[J].南方传媒研究,2009,21:8-17.
[8]MeschGS.Parentalmediation,onlineactivities,andcyberbullying[J].CyberPsychology&Behavior,2009,12(4):387-393.
[9]NicholasDF.Rumourresearchcandousedigitalwildfires[J].Nature,2013,493(7431):135.
[10]AllportGW,PostmanLJ.Thebasicpsychologyofrumor[J].TransactionsoftheNewYorkAcademyofSciences,1945,8(8):61-81.
[11]JavaA,KolariP,FininT,etal.Modelingthespreadofinfluenceontheblogosphere[C]//Proceedingsofthe15thinternationalworldwidewebconference.[s.l.]:[s.n.],2006:22-26.
[12]HillAL,RandDG,NowakMA,etal.Infectiousdiseasemodelingofsocialcontagioninnetworks[J].PLoSComputBiol,2010,6(11):e1000968.
[13]WangJ,ZhaoL,HuangR.SIRaRurumorspreadingmodelincomplexnetworks[J].PhysicaA:StatisticalMechanicsandItsApplications,2014,398:43-55.
[14]ZhaoL,CuiH,QiuX,etal.SIRrumorspreadingmodelinthenewmediaage[J].PhysicaA:StatisticalMechanicsandItsApplications,2013,392(4):995-1003.
[15]KermackWO,McKendrickAG.Acontributiontothemathematicaltheoryofepidemics[C]//ProceedingsoftheroyalsocietyofLondona:mathematical,physicalandengineeringsciences.[s.l.]:TheRoyalSociety,1927:700-721.
[16]AveryC,ZemskyP.Multidimensionaluncertaintyandherdbehaviorinfinancialmarkets[J].AmericanEconomicReview,1998,88(4):724-748.
[17] 李 慧.从文献信息老化到网络信息老化的研究分析[J].情报科学,2010(3):384-388.
[18]TakayasuM,SatoK,SanoY,etal.Rumordiffusionandconvergenceduringthe3.11earthquake:atwittercasestudy[J].PlosOne,2015,10(4):e0121443.
[19] 戴世富,王 颖.网络谣言的成因及应对策略初探—“3·16”抢盐事件的传播学解读[J].新闻界,2011(4):11-12.
[20]BikhchandaniS,HirshleiferD,WelchI.Learningfromthebehaviorofothers:conformity,fads,andinformationalcascades[J].JournalofEconomicPerspectives,1998,12(3):151-170.
[21] 刘天华,张志华,李大伟,等.Weibull分布更新函数的指数近似算法[J].北京航空航天大学学报,2012,38(6):816-818.
[22] 张士峰.Weibull型产品的可靠性验证[J].国防科技大学学报,2001,23(4):16-19.
[23]KoopmanJ.Modelinginfectiontransmission[J].Annu.Rev.PublicHealth,2004,25:303-326.
[24] 赵来军,吴 盼.考虑传播率和移出率变化的谣言传播规律研究[J].上海理工大学学报,2014,36(4):345-350.
[25] 丁学东.文献计量学基础[M].北京:北京大学出版社,1993.
[26]BrookesBC.Obsolescenceofspeciallibraryperiodicals:samplingerrorsandutilitycontours[J].JournaloftheAmericanSocietyforInformationScience,1970,21(5):320-329.
[27] 段宇锋.网络信息资源老化规律研究[J].图书情报知识,2005(4):28-31.
[28]ThomasSA.Lies,damnlies,andrumors:ananalysisofcollectiveefficacy,rumors,andfearinthewakeofKatrina[J].SociologicalSpectrum,2007,27(6):679-703.
Research on Online Business Rumors Transmission Based on an Improved SIR Model
YU Sha-sha1,WANG You-guo1,ZHU Liang2
(1.College of Science,Nanjing University of Posts and Telecommunications,Nanjing 210046,China;2.College of Telecommunications & Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)
The information transmission mechanism in social network is researched and propagation process of mathematical model is established.Through analyzing the characteristics of the transmission for information in social networks,combined with the effect of herd behaviour in transmission dynamics and information obsolescence,on the basis of classical SIR model,the information transmission model in accordance with rumor propagation characteristics in online social network is established,and the numerical simulation of the changing trend of the number of states in networks is carried out.In particular,the online business rumors and the effect of employing Net-cheaters to refute a rumor are analyzed.The experiments show that it has found the optimal time point to make the economic losses to the minimum and inhibits the spread of rumor effectively.Additionally,the result provides relevant departments with a theoretical analysis on the cyberspace public opinion.
social network;epidemic model;herd effect;information obsolescence;business rumors
2016-01-25
2016-05-11
时间:2016-10-24
国家自然科学基金资助项目(61179027);江苏省“青蓝工程”基金(QL06212006);江苏省高校研究生科研创新计划项目(KYLX15_0831)
余莎莎(1990-),女,硕士研究生,研究方向为信号处理理论与应用;王友国,博士生导师,教授,研究方向为信息理论及应用、编码理论与应用、随机共振理论与研究。
http://www.cnki.net/kcms/detail/61.1450.TP.20161024.1114.054.html
TP39
A
1673-629X(2016)11-0195-05
10.3969/j.issn.1673-629X.2016.11.042
