改进的三次指数平滑法及其在车联网中的应用
2016-02-27杨济瑞赵海涛刘南杰
杨济瑞,赵海涛,刘南杰
(1.南京邮电大学 通信与信息工程学院,江苏 南京 210003;2.南京邮电大学 网络基因工程研究所,江苏 南京 210003)
改进的三次指数平滑法及其在车联网中的应用
杨济瑞1,2,赵海涛1,2,刘南杰1,2
(1.南京邮电大学 通信与信息工程学院,江苏 南京 210003;2.南京邮电大学 网络基因工程研究所,江苏 南京 210003)
指数平滑法是车联网中交通流预测较为常见的方法之一,其准确性主要取决于平滑系数。由于传统指数平滑法系数是静态的原因,其已经不能满足交通流预测的精度要求。为了进一步提高预测精度,对传统指数平滑法进行了分析,其平滑系数相对静态,不能实时进行修正,导致其不能很好地反映数据变化的实时趋势。通过利用三次指数平滑法对交通流预测模型进行优化,利用等距法寻找每次预测时的最优平滑系数对数据趋势进行估计,保证了每次预测时的平滑系数最优,提高了预测精度。基于交通流预测的不同应用环境,利用南京某路段实际的交通流数据进行仿真,得到的仿真结果表明,提出的优化算法在预测交通流数据变化趋势方面有较高的精度。
车联网;指数平滑法;最优平滑系数;交通流预测
0 引 言
随着大数据时代的到来,社会各领域产生了海量的数据。车联网作为物联网重要的一个分支,也产生了大量的交通数据。现今的交通流数据一般是由浮动车设备采集的,能够反映交通流数据特征[1-2]。交通流预测对于交通管理和城市交通道路规划等具有重要意义。
指数平滑法是一种短期时间序列的预测方法,简单易行,应用广泛,能够充分利用历史数据进行预测,是仅次于回归预测法应用最为广泛的预测方法之一,且成为组合预测中的首选方法。国内外对此也做了很多研究。文献[3-5]针对平滑系数提出了一些改进方法。文献[6]研究了一种双指数平滑法模型。文献[7]研究了四种时间序列模型的预测,表明了指数平滑法要比其他方法对时间序列模型的预测更为准确。文献[8]介绍了一种基于指数平滑法的二进制树递归分区的监测方法。文献[9]建立了参数最优的二次和三次指数平滑法预测模型。文献[10]通过优化平滑系数和平滑初值对指数平滑法做了改进。文献[11]介绍了寻找平滑系数α的多种方法,并分析了各方法的优劣。
传统的指数平滑法系数是静态的,即对于不同时段的数据变化不能呈现出很好的自适应能力,这显然一定程度上影响了预测精度。为了更好地服务大众出行和交通管理,需要提高预测精度。因此,有必要对传统的指数平滑法进行改进。文中在前人研究的基础上,提出一种能够使平滑系数自适应的优化算法。每次预测时通过等距法寻找最优的平滑系数α,使得平滑系数不断得到更新,预测模型得到优化。通过交通流实例仿真结果表明,优化的指数平滑法在整体上有更好的预测效果。
1 指数平滑法
指数平滑法的基本思想是历史时间越近的数据对预测的影响越大,历史时间越远的数据对预测的影响越小。利用平滑平均数将序列的差异抽象化,对历史的统计数据进行加权修匀以区分基本数据模式和随机变动。这样获得时间序列的平滑值,并作为未来短期时间的预测值。
指数平滑法的一次指数和多次指数计算公式分别如式(1)和式(2)所示。
st=αxt+(1-α)st-1
(1)
(2)
式中,st为t时刻的平滑值;α为平滑系数,一般取值为0<α<1;xt为历史数据序列。
若将t分别用t-1,t-2,…代入式(1)可得:
(3)

图1显示了α取不同值时的加权系数曲线图。
在图1中,当α=0.5,i=10时,α(1-α)10≈0.000 49,由此可见,在历史时段10之前的数据对预测结果已经没有实际意义了。当α=0.2,i=10时,α(1-α)10≈0.021,此时的历史时段10附近的数据对预测仍有一定的作用[13]。α的取值一旦固定,则加权系数也随之固定。在预测过程中,模型不能自动调整以及时反映数据的变化情况,从而使得预测结果和实际值之间的误差越来越大。明显可得,如果数据的走势是一直递增,那么按照传统的指数平均法预测出的结果必然比实际值偏低。α值的大小体现了不同指标在预测中的作用。因此,如果利用预测误差的大小对预测模型的加权系数进行自适应调整,则模型的预测精度将有一定的提高。

图1 不同取值的α对应的加权系数曲线
2 改进的三次指数平滑法
指数平滑法按次数可分为一次指数平滑法、二次指数平滑法和三次指数平滑法等。一次指数平滑法适用于无趋势效应、呈平滑趋势的时间序列的预测和分析;二次指数平滑法多适用于呈线性变化的时间序列预测[14]。由于交通流数据变化呈非线性变化趋势,所以比较适合用三次指数平滑法进行预测。优化的三次指数平滑法模型如图2所示。
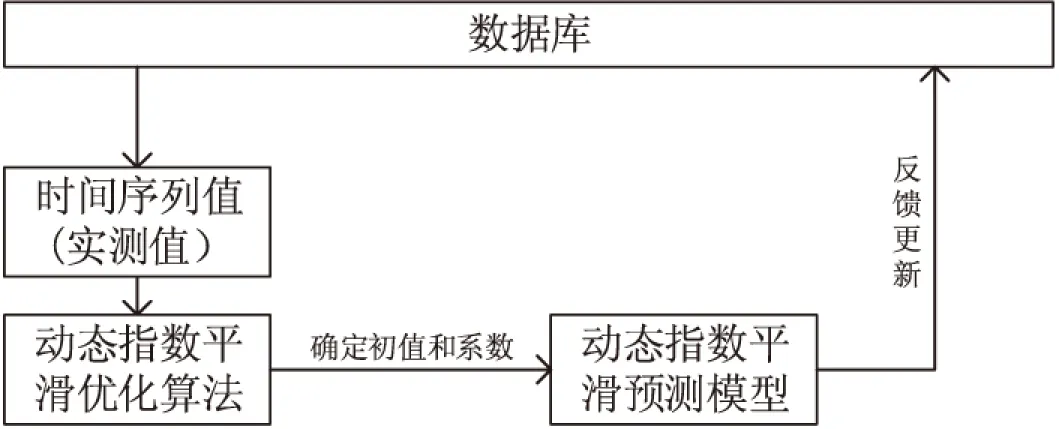
图2 优化的三次指数平滑法模型
三次指数平滑法的公式为:
(4)

时段t+n的交通流数据预测公式为:
(5)
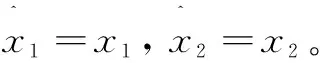
预测参数at,bt,ct分别为:
(6)
由于指数平滑法“重近轻远”的特点,在历史数据较多的情况下,初值对预测的影响不大,反之,在历史数据较多的情况下可用简单的平均法获得初值。所以统一采用计算历史数据的算术平均法确定平滑初值。
预测效果的优劣是依据预测值和实际值的误差大小判定的。误差越小,说明预测越精确。文中引用平方和误差进行误差的判定,具体算法和证明在文献[10]中有介绍,此处不再赘述。误差平方和公式为:
(7)
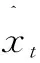
为了使三次指数平滑系数能动态化,首先将式(4)中三个基本公式展开,得:
(8)
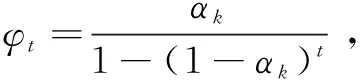
(9)
新的预测公式为:
(10)
此时的预测参数为:
(11)
文中在确定每次的αk时,采用了等距法进行搜索最优值。在搜索前先确定距长λ,以λ=0.01为例:
Step1:选定M个连续时段的历史研究数据。确定出平滑初值,设定距长λ=0.01,则将α分成100个相同的距离区间,记为αk(k=1,2,…)。
Step2:取αk=0.01,计算出对应的minSSE值。
Step3:取αk=0.02,计算出对应的minSSE值,以此类推,重复Step3,直到所有的αk计算完毕,求出所有对应的minSSE值。
Step4:选择最小minSSE值对应的αk值,这个值就是用作预测的最优α值。
确定了预测M+1时段的最优α值,可得到M+1时段的预测值。在下次确定新的最优α值时,去掉最早的一个数据,加入实测的M+1时段数据,组成一个新的M个历史研究数据,重复Step1-Step4。整个算法流程如图3所示。

图3 平滑系数α的优化流程算法
3 交通流预测环境
在交通流预测中应用优化的三次指数平滑模型,采用江苏南亿迪纳数字科技发展有限公司云平台数据库中南京某直行路段某天的车流量作为样本数据序列,如表1所示。
在Windows平台下,借助Java编程语言编程获取每次的αk,利用MATLAB软件对预测结果作图,得出的传统方法预测值和改进方法预测值如图4所示。
从图中可以看出,改进方法在一定程度上提高了预测精度。

表1 南京某直行路段车流量
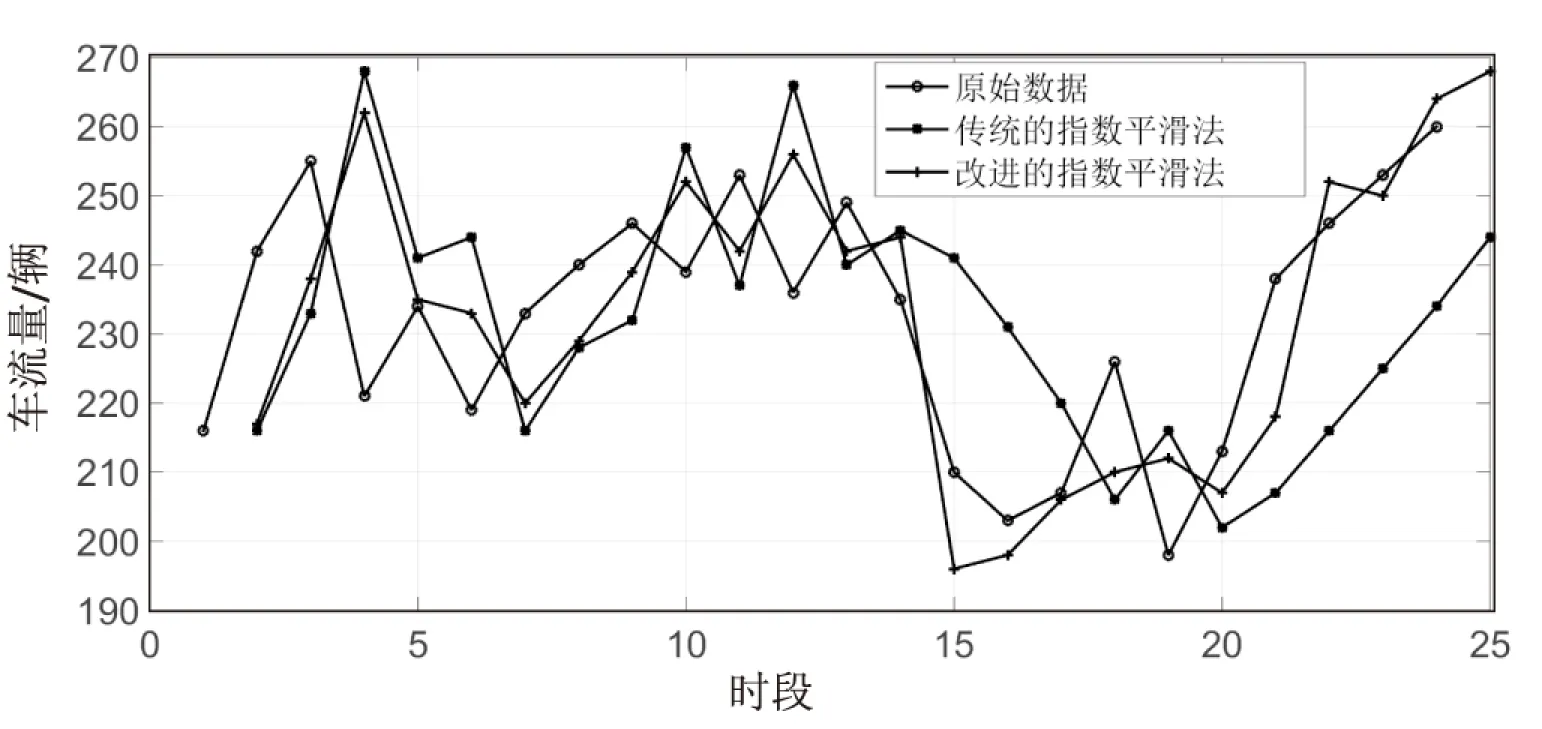
图4 两种预测方法对比图
图5为两种预测方法的相对误差,可以得出,改进的三次指数平滑法预测误差更小,精度更高。
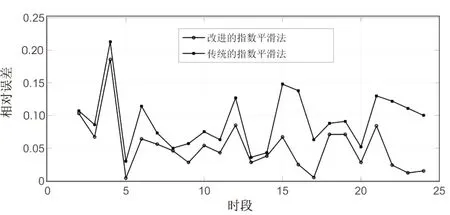
图5 两种方法预测结果和实际值的相对误差对比图
4 结束语
文中针对传统的指数平滑法模型的缺陷,提出一种能够使平滑系数自适应的优化算法,对三次指数平滑法进行改进。利用等距法寻找minSSE误差平方和最小时的最优α。通过交通流环境仿真分析,该改进的三次指数平滑法有效地提高了三次指数平滑法的预测精度。
[1]ZhangZ,YangD,ZhangT,etal.Astudyonthemethodforcleaningandrepairingtheprobevehicledata[J].IEEETransactionsonIntelligentTransportationSystems,2013,14(1):419-427.
[2]LaiKK,YuL,WangShouyang,etal.Hybridizingexponentialsmoothingandneuralnetworkforfinancialtimeseriespredication[C]//Internationalconferenceoncomputationalscience.Berlin:Springer,2006:493-500.
[3] 张忠平.指数平滑法[M].北京:中国统计出版社,1996:36-49.
[4] 金旭星,盛奎川.指数平滑参数与初值的选取研究[J].江南大学学报:自然科学版,2005,4(3):316-319.
[5] 唐炎森.指数平滑预测公式与平滑系数[J].统计与信息论坛,1998(1):39-44.
[6]KhooMBC,WongVH.Adoublemovingaveragecontrolchart[J].CommunicationsinStatistics-SimulationandComputation,2008,37(8):1696-1708.
[7]EIEmaryIM,AIRabiaAI.Estimationtechniquesformonitoringandcontrollingtheperformanceofthecomputercommunicationnetworks[J].AmericanJournalofAppliedSciences,2005,2(10):1395.
[8]SparksR,OkugamiC,BoltS.Outbreakdetectionofspatio-temporallysmoothedcrashes[J].OpenJournalofSafetyScienceandTechnology,2012,2:98-107.
[9] 刘造保,徐卫亚,张开普,等.基于改进指数平滑法的岩体边坡变形预测[J].河海大学学报:自然科学版,2009,37(3):313-316.
[10] 吴德会.动态指数平滑预测方法及其应用[J].系统管理学报,2008,17(2):151-155.
[11] 李 颖.时间序列指数平滑算法的改进研究[D].阜新:辽宁工程技术大学,2009.
[12] 陈 娟,吉培荣,卢 丰.指数平滑法及其在负荷预测中的应用[J].三峡大学学报:自然科学版,2010,32(3):37-41.
[13] 冮龙晖.基于数据融合的城市快速路交通参数短时预测方法研究[D].长春:吉林大学,2004.
[14] 王国权,王 森,刘华勇,等.基于自适应的动态三次指数平滑法的风电场风速预测[J].电力系统保护与控制,2014,42(15):117-122.
Modified Cubic Exponential Smoothing Algorithm and Its Application on IoV
YANG Ji-rui1,2,ZHAO Hai-tao1,2,LIU Nan-jie1,2
(1.College of Communication and Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China;2.Institute of Network DNA Engineering,Nanjing University of Posts and Telecommunications, Nanjing 210003,China)
The method of exponential smoothing is one of more common methods for forecasting the traffic flow in IoV (Internet of Vehicle),the accuracy of which depends on the smoothing coefficient.This method has been unable to meet the need of accuracy while forecasting traffic flow because of the static smoothing coefficient.By analyzing the features of the traditional exponential smoothing method,it is pointed out that the changing trend of data can’t be reflected appropriately using this method due to the static smoothing coefficient.Then the cubic exponential smoothing method is proposed aiming at further improving the forecasting accuracy.The changing trend of data can be forecasted through searching for the optimal smoothing coefficient using the equal interval method after optimizing the model of forecasting traffic flow by the cubic exponential smoothing method.Finally,the actual data of traffic flow on one segment in Nanjing is simulated based on different application environments where the traffic flow is forecasted.The simulation results show that the accuracy of the proposed optimization algorithm is better in terms of forecasting the changing trend of data in traffic flow.
IoV;exponential smoothing method;optimal smoothing coefficient;traffic flow forecasting
2016-01-16
2016-04-21
时间:2016-10-24
国家自然科学基金资助项目(61302100,61471203);教育部博士点基金资助项目(20133223120002)
杨济瑞(1992-),男,硕士研究生,研究方向为车联网、移动通信;赵海涛,博士,副教授,研究方向为车联网资源优化;刘南杰,博士,教授,研究方向为泛在通信、车联网、智能交通。
http://www.cnki.net/kcms/detail/61.1450.TP.20161024.1113.024.html
TP301
A
1673-629X(2016)11-0164-04
10.3969/j.issn.1673-629X.2016.11.036
