分数阶复Lorenz混沌系统的控制与同步

虞继敏，武卫红，周尚波，雷 烈，谭礼健

(1.重庆邮电大学 自动化学院,重庆 400065；2.重庆大学 计算机学院,重庆 400044)

分数阶复Lorenz混沌系统的控制与同步

虞继敏1，武卫红1，周尚波2，雷 烈1，谭礼健1

(1.重庆邮电大学 自动化学院,重庆 400065；2.重庆大学 计算机学院,重庆 400044)

基于分数阶非线性系统稳定性理论，设计了线性反馈控制器，实现分数阶复动力学系统的控制；基于矩阵配置控制器的设计方法，实现分数阶复动力学系统的同步。以分数阶复Lorenz系统为例，分别分离原系统各个变量的实部和虚部，研究了分数阶复Lorenz混沌系统的控制问题和同步问题。对分数阶复Lorenz系统的混沌特性进行了分析，然后基于分数阶非线性系统稳定性理论进行了阐述。通过设计反馈控制器，实现了分数阶复Lorenz系统的混沌控制，然后基于分数阶非线性系统稳定性理论，利用矩阵配置方法设计线性反馈控制器，实现分数阶复Lorenz混沌系统的同步。数值仿真实验结果表明，所设计的两种控制器是有效的。

分数阶；混沌系统；混沌控制；同步

0 引 言

分数阶微积分的提出已有300年历史，但人们对其几何解释和应用的进一步了解仍然少之甚少，也就是在最近二十几年里，分数阶微积分才在许多的科学与技术方面得到广泛应用。目前，分数阶微积分已经广泛应用于非线性动力学系统控制、金融学、化学和数理科学等诸多领域[1-4]。

迄今，随着分数阶非线性动力学系统在控制科学与工程领域的不断发展，人们发现分数阶非线性系统在许多情况下都存在复杂的混沌现象，为此也开始了对分数阶非线性系统的混沌控制和混沌同步研究[5-10]。但由于研究者对分数阶混沌系统的研究起步较晚，所以许多理论和技术仍有待进一步研究和完善。

现今，对于混沌系统，大多是研究其在实动力系统中的各种性能指标，而对复动力系统中混沌的特性以及各项性能指标的研究相对较少。复Lorenz方程是在1982年由Fowler和Gibbon[11]提出的，不仅在物理领域，在其他领域也起到了很重要的作用，尤其是在混沌保密通信系统中。由于复系统是实系统的延伸，比实系统多出了虚数部分，它所传输的信息和内容也相应地增加。

近年来，分数阶复系统的混沌特性、混沌控制与同步研究得到了广泛的关注，例如，分数阶复Chen系统[12]、分数阶复Lorenz系统[13]、自适应同步[14]、完全同步[15]、投影同步[16]、脉冲同步[17-18]、广义同步[19]等等。

文中对分数阶复动力系统的混沌特性、混沌控制及其同步进行了研究。

1 分数阶时滞复Lorenz系统

分数阶复Lorenz系统的数学模型如下：

(1)

分离系统(1)各个变量的实部和虚部，则有：

(2)

其中，分数阶微分阶次0<α≤1。

分离后的系统变为分数阶非线性系统，当α=0.995，a1=10，a2=110，a3=2，初始值取x1(0)=7，x2(0)=8，x3(0)=5，x4(0)=6，x5(0)=12时，系统是混沌的。于是，此时的系统也就相当于分数阶非线性混沌系统。

利用Matlab数值仿真，得到分数阶复Lorenz系统混沌吸引子,如图1所示。

2 分数阶复Lorenz混沌系统的控制

本节基于分数阶非线性系统的稳定控制理论，研究如何实现分数阶复Lorenz系统的混沌控制。

针对分数阶非线性系统稳定性问题，提出了如下的稳定性理论。

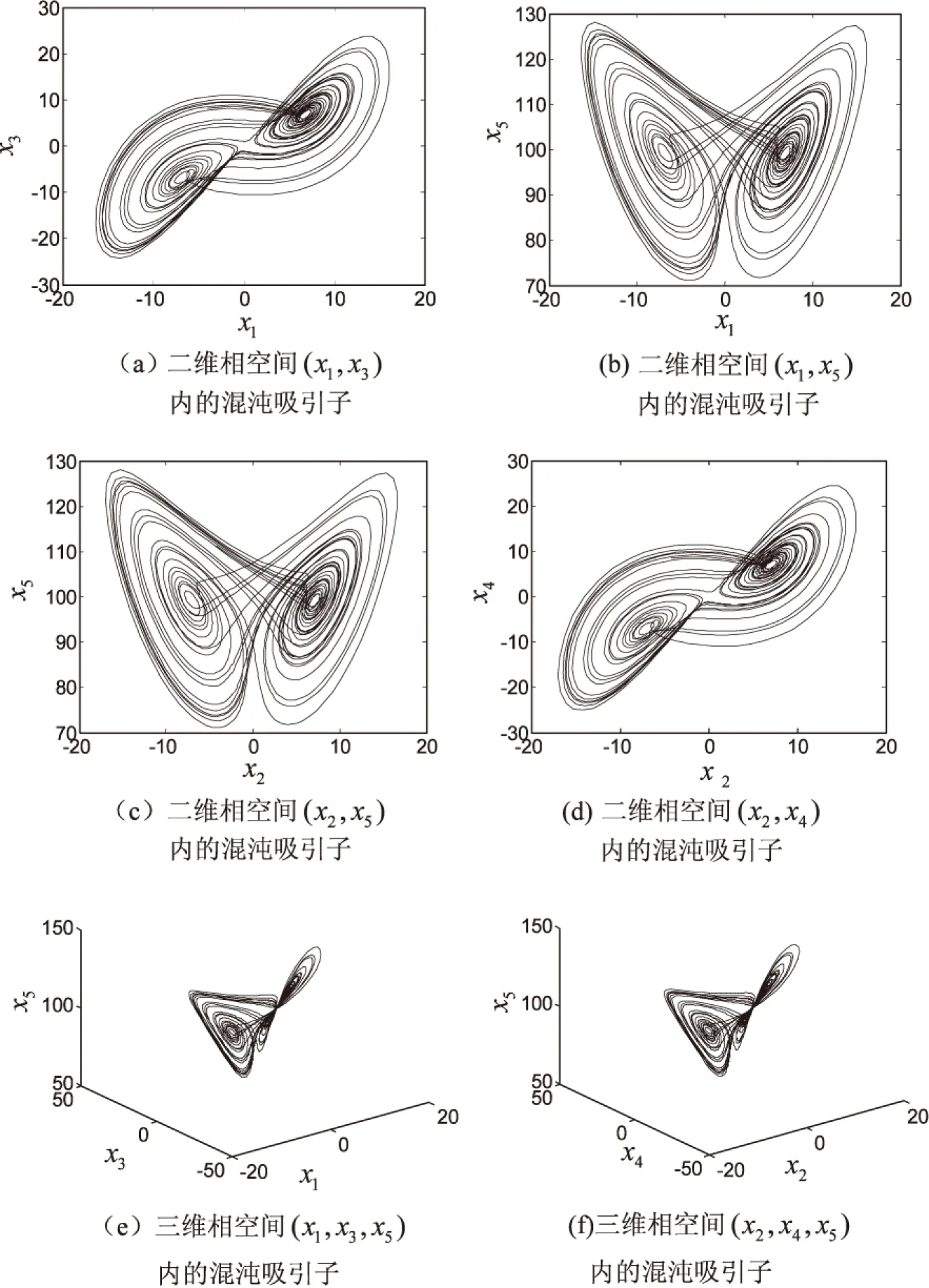
图1 分数阶复Lorenz系统混沌吸引子

定理1[20]：对于分数阶复Lorenz混沌系统,当系统阶数α<1时,对任意状态变量x(t)∈Rn,存在正定矩阵P,使式(3)恒成立,则该系统稳定。

(3)

为实现式(2)的混沌控制，设计如下的线性反馈控制器：

(4)

根据定理1，假设正定矩阵P为单位对角矩阵，构造如下函数：

当k1≥45，k2≥45，k3≥-1，k4≥-1，k5≥0时数h(x)≤0，系统(5)稳定。取k1=100，k2=100，k3=20，k4=30，k5=1进行数值仿真,仿真结果如图2所示。仿真结果表明，系统(5)渐近稳定,这验证了根据定理设计的控制器有效。

图2 系统中变量x1,x2,x3,x4,x5随N的演化图

3 分数阶复Lorenz混沌系统的同步

本节基于分数阶非线性系统稳定控制法，研究如何通过矩阵配置法设计的控制器实现分数阶复Lorenz系统在响应系统的混沌同步。

以系统(2)为驱动系统，定义响应系统为：

(6)

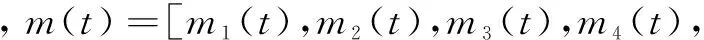
m5(t)]T是待设计的控制器。

定义系统的同步误差为：e1(t)=x1(t)-y1(t)，e2(t)=x2(t)-y2(t)，e3(t)=x3(t)-y3(t)，e4(t)=x4(t)-y4(t)，e5(t)=x5(t)-y5(t)。

由驱动系统(2)和响应系统(6)可以得到同步误差系统:

(7)

将该误差系统进行改写:

(8)

同步的核心是如何设置控制器m(t)。

针对分数阶非线性系统稳定性问题，提出了如下的稳定性理论：

定理2[20-21]：若矩阵A(x(t))的状态变量满足以下条件：

(1)aij=-aij(i≠j)；

(2)aii≤0，i=1,2,…,n(其中aii不全为零)。

那么分数阶非线性系统(2)稳定。根据稳定性理论，该误差系统稳定。

证明：

构造函数：

(9)

根据定理1，满足上述条件的系统稳定。

如果设计的控制器和未知参数能使误差系统满足：

(10)

设正定矩阵P为单位对角矩阵，则有：

根据定理2，该误差系统稳定。由此，得到所需设计的控制器：

m1(t)=(a1+a2-y5(t))e1(t)+y3(t)e3(t)

m2(t)=(a1+a2-y5(t))e4(t)+y4(t)e4(t)

(12)

将所设计的控制器和未知参数辨识规则进行数值仿真，如图3所示。

仿真结果验证了所设计控制器和未知参数辨识规则的有效性。

4 结束语

基于分数阶系统稳定性理论，文中通过分离原系统各个变量的实部和虚部，将原系统转化为分数阶多时滞实Lorenz系统来实现分数阶复Lorenz混沌系统的控制；基于矩阵配置控制器的设计方法，同样通过分离原系统各个变量的实部和虚部来实现分数阶混沌系统的同步。数值仿真验证了文中研究的有效性。将原系统加入时滞后，基于矩阵配置法无法实现系统同步，这将是下一步的研究方向。

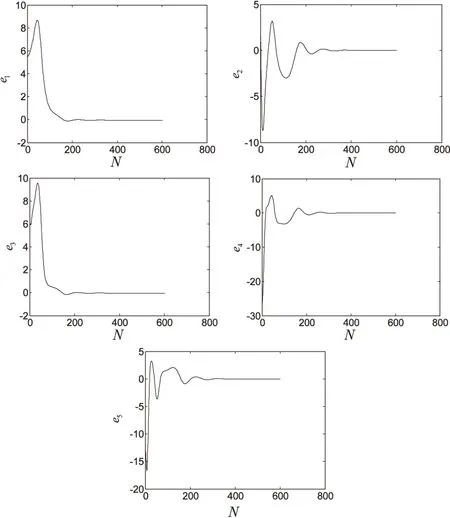
图3 同步误差e1，e2，e3，

[1] 曹建秋,肖华荣,蓝章礼,等.基于数字图像比特面的混沌加密方法[J].计算机技术与发展,2010,20(8):133-136.

[2] 王 斌,蒲亦非,周激流.一种新的分数阶微分的图像边缘检测算子[J].计算机应用研究,2012,29(8):3160-3162.

[3] 张丽敏,周尚波.基于分数阶微分的尺度不变特征变换图像匹配算法[J].计算机应用,2011,31(4):1019-1023.

[4] 徐 强,包伯成,胡 文,等.分数阶混沌系统数值解析与电路仿真研究倡[J].计算机应用研究,2010,27(12):4612-4614.

[5] 王明军,王兴元.基于一阶时滞混沌系统参数辨识的保密通信方案[J].物理学报,2009,58(3):1467-1472.

[6] 张芳芳,刘树堂,余卫勇.时滞复Lorenz混沌系统特性及其自时滞同步[J].物理学报,2013,62(22):220505.

[7] 高 心.分数阶动力学系统的混沌,控制和同步的研究[D].西安:电子科技大学,2005.

[8] 李 睿,张广军,朱 涛,等.不同阶混沌系统广义混合错位函数投影同步及在保密通信中的应用[J].计算机应用,2014,34(7):1915-1918.

[9] 蒋逢灵.分数阶混沌系统同步及其在保密通信中的应用[D].湘潭:湖南科技大学,2012.

[10]YuJ,WuW,WangC,etal.AstabilitycontrolmethodoffractionalcomplexLorenzsystemwithtime-delay[C]//Internationalconferenceonintelligenthuman-machinesystemsandcybernetics.[s.l.]:IEEE,2015:464-467.

[11]FowlerAC,GibbonJD,McGuinnessMJ.ThecomplexLorenzequations[J].PhysicaD:NonlinearPhenomena,1982,4(2):139-163.

[12]LuoC,WangX.Chaosgeneratedfromthefractional-ordercomplexChensystemanditsapplicationtodigitalsecurecommunication[J].InternationalJournalofModernPhysicsC,2013,24(4):1350025.

[13]LuoC,WangX.Chaosinthefractional-ordercomplexLorenzsystemanditssynchronization[J].NonlinearDynamics,2013,71(1-2):241-257.

[14] 张若洵,杨 洋,杨世平.分数阶统一混沌系统的自适应同步[J].物理学报,2009,58(9):6039-6044.

[15]MahmoudGM,MahmoudEE.Completesynchronizationofchaoticcomplexnonlinearsystemswithuncertainparameters[J].NonlinearDynamics,2010,62(4):875-882.

[16] 刘 杰,陈士华,陆君安.统一混沌系统的投影同步与控制[J].物理学报,2003,52(7):1595-1599.

[17]WangX,ZhangY,LinD.Impulsivesynchronizationofhyperchaoticaclassoffractional-ordersystems[J].ChinesePhysicsB,2011,20(3):88-94.

[18] 毛北行,王东晓,卜春霞.Lurie混沌系统的脉冲控制同步[J].华中师范大学学报:自然科学版,2012,46(3):297-299.

[19] 王兴元,孟 娟.超混沌系统的广义同步化[J].物理学报,2007,56(11):6288-6293.

[20] 赵灵冬.分数阶非线性时滞系统的稳定性理论及控制研究[D].上海:东华大学,2014.

[21] 李安平,刘国荣,深细群.不同阶分数阶混沌系统的同步与参数辨识[J].计算机工程与应用,2013,49(4)：245-248.

Control and Synchronization of Fractional Complex Lorenz Chaotic System

YU Ji-min1,WU Wei-hong1,ZHOU Shang-bo2,LEI Lie1,TAN Li-jian1

(1.College of Automation,Chongqing University of Posts and Telecommunications, Chongqing 400065,China;2.Department of Computer Science,Chongqing University,Chongqing 400044,China)

Based on the stability theorem of the fractional nonlinear system,the stability control of fractional chaotic system is realized by a linear feedback controller designed,and based on the method of the matrix configuration,the synchronization of fractional chaotic system is implemented.Taking fractional complex Lorenz system as an example,the real part and imaginary part of each variable in original system is separated to study the problem of synchronization and chaos control.Firstly,chaotic characteristics of fractional complex Lorenz system are analyzed,and the stability theorem based on the fractional-order nonlinear system is discussed.The stability control of fractional chaotic system is realized by a linear feedback controller designed.Then,based on the stability theorem of the fractional-order nonlinear system,the chaotic system synchronization is implemented by using matrix configuration method.The numerical simulation confirms the efficiency of the proposed control method and synchronization method.

fractional order;chaos system;chaotic control;synchronization

2016-01-29

2016-05-11

时间：2016-10-24

中央高校业务基金重大项目(106112014CDJZR188801)；重庆市前沿与应用基础研究项目(cstc2014jcyjA40037)

虞继敏(1964-),男,教授,博士,研究方向为非线性系统控制理论与应用、分数阶系统控制理论；武卫红(1989-),男,硕士研究生,研究方向为混沌及其控制、非线性控制理论。

http://www.cnki.net/kcms/detail/61.1450.TP.20161024.1117.072.html

TP31

A

1673-629X(2016)11-0130-04

10.3969/j.issn.1673-629X.2016.11.029