基于偏微分方程的乘性噪声去噪算法
2016-02-27张化朋任少美
张化朋,任少美
(南京邮电大学 理学院,江苏 南京 210046)
基于偏微分方程的乘性噪声去噪算法
张化朋,任少美
(南京邮电大学 理学院,江苏 南京 210046)
图像去噪是图像处理中最基本的问题,也是当前研究的热点。近年来,国内外学者对去除乘性噪声进行了大量的研究,在AA模型的基础上提出了许多去除合成孔径雷达图像中的伽马噪声的模型,它们都可以有效地去除图像中的噪声,但是共同的缺点是原图像的细节丢失并且计算速度慢。针对这些问题,引入了权重函数,在此基础上给出一种基于偏微分方程的去除图像乘性噪声的变分模型。然后使用交替迭代法,求出了该模型的数值解,并从理论上说明了该迭代序列的收敛性。数值实验结果表明,所提出的模型保持了较好的去噪效果,能够较好地抑制图像中的“阶梯效应”;与其他模型相比,该算法处理速度快,极大地缩短了运算时间。
图像去噪;合成孔径雷达图像;伽马噪声;偏微分方程;交替迭代法
0 引 言
随着科学技术的发展,信息的交流显得尤为重要,而图像传输在信息交流中作用很大,但是图像中的各类噪声严重影响了图片的后续应用,因此图像去噪非常重要。根据噪声与信号之间的关系,图像中的噪声可以分为两类:乘性噪声和加性噪声。其中,乘性噪声广泛存在于合成孔径雷达(Synthetic Aperture Rader,SAR)图像中,如何有效去除SAR图像中的乘性噪声是SAR图像处理领域近年来研究的热点问题[1-4]。
SAR图像中的乘性噪声服从伽马(Gamma)分布,故称为伽马(Gamma)噪声。因此,如何有效地去除伽马噪声是SAR图像处理领域的首要问题。去除伽马噪声的方法有:基于小波变换、基于滤波和基于偏微分方程(Partial Differential Equation,PDE)[5-7]。其中,基于偏微分方程的去噪方法是通过变分的思想去除SAR图像中的噪声。虽然现有的模型均可以去除伽马噪声,但都存在明显的“阶梯效应”,速度也较慢。因此,目前需要解决的问题是如何在保留现有模型优势的基础上,提高去噪效果并加快去噪速度。
为了解决此问题,在文献[4]中的模型的基础上,引入参数函数[8-9],文中提出了一种新的去除SAR图像中乘性噪声的变分模型。该模型不仅较好地抑制了噪声,避免了“阶梯效应”,而且能很好地保护图像的边缘细节与纹理特征,运行速度也较快。
1 去噪模型
近年来,许多学者针对伽马噪声提出了很多基于偏微分方程的去噪模型[10-11]。Rudin等提出了RLO模型,在一定程度上可以去噪,但是会出现“阶梯效应”。Alubert和Aujor根据最大后验估计提出了AA模型,Huang等利用对数变换,提出了HNW模型:
(1)

为了利用文献[9]的思想,结合参数函数a(x):
(2)
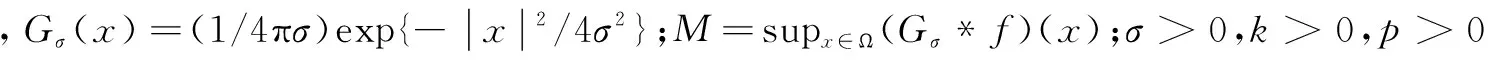
它的作用是边缘检测和控制去噪时的平滑速度。
其中,a1,t为正则化参数。
2 迭代算法及收敛性分析
受文献[4,11]的启发,利用交替最小化算法[12](AlternatingMinimizationAlgorithm,AMA)求解问题(3)。设w0为初始数据,求解下列两个优化问题:
(4)
根据交替最小化算法的思想,求解新模型的算法如下:
Step1:初始化。给定参数a1,σ,k,p,t,以及初始数据w0,并令m=1。
Step2:根据牛顿迭代法,利用式(4)求解zm。
Step3:根据数值化方法[13-14],并利用式(5)求解wm。

Step5:输出去噪后的图像。
下面证明迭代序列w0,z1,w1,z2,…,wm-1,zm的收敛。由式(4)和式(5)可知,wm=S(zm)=S(R(wm-1))=T(wm-1),因此有下面的定理。
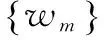
根据文献[4,11],可以通过下面几个引理证明定理1,这里不再证明定理1。
引理1:算子R是非膨胀的,算子S是1/2-平均非膨胀的,算子T是非膨胀的。
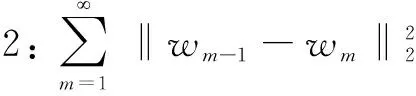
引理3:模型(2)对应的泛函是强制的。
引理4:算子T至少存在一个不动点。
3 实验结果与分析
为了验证模型的有效性及可行性,本节将在相同的计算机软件与硬件下采用MATLABR2009a对Lena和Babala图像进行仿真实验。为了定量比较,选取以下4个度量作为性能指标:信噪比(SignaltoNoiseRatio,SNR)、绝对误差(RelativeError,ReErr)、峰值信噪比(PeakSignaltoNoiseRatio,PSNR)、均方根误差(MeanSquareError,MSE)。显然,SNR和PSNR越大,去噪效果越好;MSE和ReErr越小,去噪效果越好。实验中分别对两幅图像添加视数为10、30、50的伽马噪声,并与AA模型、RLO模型、HNW模型进行比较,去噪效果见图1~3。
另外,表1~3分别给出了图1~3对应的去噪后的客观指标值。

图1 实验结果1

图2 实验结果2

图3 实验结果3
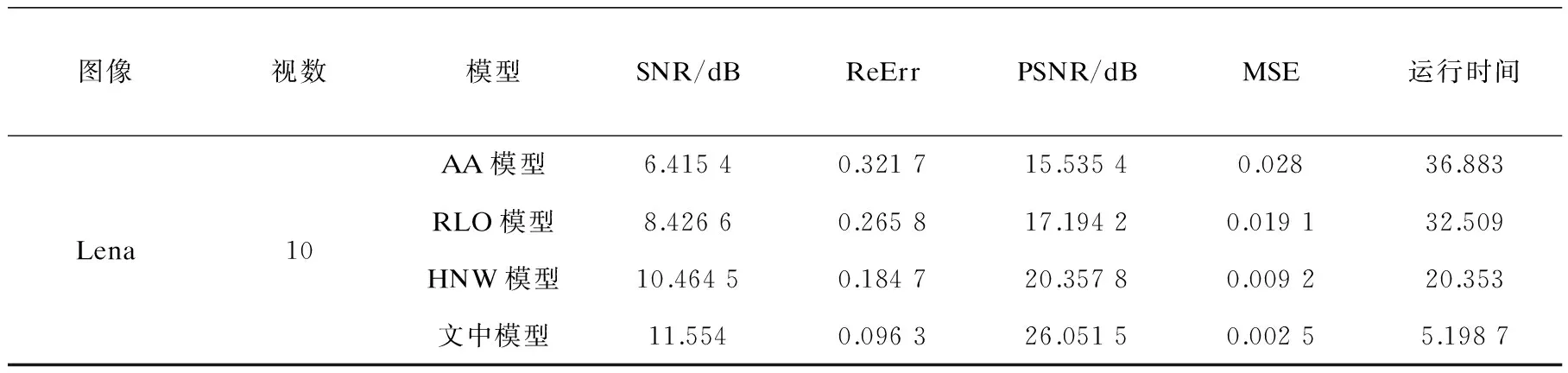
图像视数模型SNR/dBReErrPSNR/dBMSE运行时间Lena10AA模型6.41540.321715.53540.02836.883RLO模型8.42660.265817.19420.019132.509HNW模型10.46450.184720.35780.009220.353文中模型11.5540.096326.05150.00255.1987

表2 图2的数值实验结果

表3 图3的数值实验结果
从表1~3可以看出:对于人工产生的伽马噪声,比较SNR,PSNR值,文中模型都高于其他模型,而ReErr,MSE值均低于其他模型。另外,文中模型的收敛速度更快。
4 结束语
文中引入新的正则项,建立了一个新的去除SAR图像中伽马噪声的变分模型,既去除了噪声,又改善了去噪质量。
数值实验结果表明,新模型可以很好地去除噪声,并有效地抑制“阶梯效应”。
[1]RudinL,LionsP,OsherS,etal.Multiplicativedenoisinganddeblurring:theoryandalgorithm[M]//Geometriclevelsetmethodsinimaging,vision,andgraphics.NewYork:Springer,2003:103-119.
[2]AubertG,AujolJF.Avariationalapproachtoremovingmultiplicativenoise[J].SIAMJournalonAppliedMathematics,2008,68(4):925-946.
[3]JinZ,YangX.Analysisofanewvariationalmodelformultiplicativenoiseremoval[J].JournalofMathematicalAnalysis
andApplications,2010,362(2):415-426.
[4]HuangY,NgM,WenY.Anewtotalvariationmethodformultiplicativenoiseremoval[J].SIAMJournalonImagingSciences,2009,2(1):20-40.
[5]DonohoDL,JohnstoneM.Adaptingtounknownsmoothnessviawaveletshrinkage[J].JournaloftheAmericanStatisticalAssociation,1995,90(432):1200-1224.
[6]GemanD,GemanS.Stochasticrelaxation,Gibbsdistributions,andtheBayesianrestorationofimages[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,1984(6):721-741.
[7]RudinL,OsherS,FatemiE.Nonlineartotalvariationbasednoiseremovalalgorithms[J].PhysicaD:NonlinearPhenomena,1992,60(1):259-268.
[8]StrongDM,ChanTF.Spatiallyandscaleadaptivetotalvariationbasedregularizationandanisotropicdiffusioninimageprocessing[C]//Diusioninimageprocessing,UCLAmathdepartmentcamreport.[s.l.]:[s.n.],1996.
[9]DongG,GuoZ,WuB.Aconvexadaptivetotalvariationmodelbasedonthegraylevelindicatorformultiplicativenoiseremoval[C]//Abstract&appliedanalysis.[s.l.]:HindawiPublishingCorporation,2013.
[10] 胡学刚,张龙涛,蒋 伟.基于偏微分方程的变分去噪模型[J].计算机应用,2012,32(7):1879-1881.
[11] 胡学刚,楼越芳.一种去除Gamma乘性噪声的全变分模型[J].四川大学学报:工程科学版,2014,46(2):59-65.
[12]WangY,YangJ,YinW,etal.Anewalternatingminimizationalgorithmfortotalvariationimagereconstruction[J].SIAMJournalonImagingSciences,2008,1(3):248-272.
[13] 张红英,彭启琮.变分图像复原中PDE的推导及其数值实验[J].计算机工程与科学,2006,28(6):44-46.
[14]ShenJ,ChanTF.Mathematicalmodelsforlocalnontextureimpaintings[J].SIAMJournalonAppliedMathematics,2002,62(3):1019-1043.
Algorithm of Removing Multiplicative Noise Based on Partial Differential Equation
ZHANG Hua-peng,REN Shao-mei
(College of Science,Nanjing University of Posts and Telecommunications,Nanjing 210046,China)
Image denoising is the most basic problem in image processing and also the current research focus.In recently years,there are a lot of researches on the multiplicative noise removal by domestic and foreign scholars.Based on AA model,many models for removal of Gamma noise in synthetic aperture radar image are proposed,which can remove the noise effectively,but the common disadvantage is loss of the original image’s detail and slow computing speed.Aiming at them,introducing weight function,a new variational model based on partial differential equation is proposed to remove the multiplicative noise.An alternating minimization algorithm is introduced to solve the problem for the model.What’s more,the convergence for the variational problem is illustrated in theroy.Experimental results show that the proposed model has a good denoising effect and restrains the “staircase effect”.Compared with the other models,the algorithm is faster and greatly decreases the computational time.
image denoising;synthetic aperture radar image;Gamma noise;Partial Differential Equation (PDE);alternating minimization algorithm
2016-01-23
2016-05-18
时间:2016-10-24
国家自然科学基金资助项目(11301281)
张化朋(1982-),男,副教授,博士,研究方向为模糊泛函分析;任少美(1989-),女,硕士研究生,研究方向为图像处理。
http://www.cnki.net/kcms/detail/61.1450.TP.20161024.1117.080.html
TP301.6
A
1673-629X(2016)11-0090-03
10.3969/j.issn.1673-629X.2016.11.020
