基于节点最大剩余容量的负荷再分配策略研究
2016-02-27周添杰蒋国平
周添杰,蒋国平
(南京邮电大学 自动化学院,江苏 南京 210023)
基于节点最大剩余容量的负荷再分配策略研究
周添杰,蒋国平
(南京邮电大学 自动化学院,江苏 南京 210023)
主要研究目的是在复杂网络发生相继故障的过程中,设计一种合理有效的复杂网络相继故障的负荷再分配策略,有效减小网络临界阈值βm,提高网络鲁棒性。通过对比研究和仿真建模的方法,提出了基于节点最大剩余容量的负荷再分配策略:当网络中节点发生故障时,故障节点的负荷分配给当前时刻网络内剩余容量最大的部分节点,这部分节点的个数与故障节点的度在数值上相等,并且这部分节点所能分得的负荷与其自身的剩余容量有关,剩余容量越大的节点相对而言所能分得的负荷越多。选取人工网络和实际网络进行仿真对比研究,结果表明,所提出的负荷再分配策略能够有效地减小临界阈值βm,说明该策略是合理有效的,能够提高网络鲁棒性。
复杂网络;相继故障;负荷再分配;网络鲁棒性
1 概 述
随着科学技术的进步和发展,现代社会已然是一个网络化的社会,人类的生产生活已经离不开网络,时时刻刻都在接触电力网[1]、互联网[2]、交通网、信息网[2]、人际关系网[2]等各种各样的网络。在实际生产生活中,网络中的极少部分节点在发生故障时,会通过网络中节点与节点之间的耦合关系扩大故障规模,最终导致网络中的大部分节点甚至整个网络发生故障,称这一现象为“网络雪崩”[3],也称为复杂网络的相继故障。网络的相继故障具有很强的破坏性。例如,2003年8月,由美国俄亥俄州的3条高压线路过载所引起的北美大停电事件[4],使数千万人陷入黑暗,并导致了无法估量的经济损失。
为了采取有效措施来减小或抑制网络相继故障的规模,针对网络相继故障这一现象的研究有其必要性,近年来很多专家学者已经取得了积极的成果。就复杂网络相继故障的模型而言,有六类模型被各界学者广为研究:负荷-容量模型、二值影响模型[5]、OPA模型[6]、沙堆模型[7]、CASCADE模型[8]、耦合映像格子模型[9]。其中,应用最为广泛的是负荷-容量模型。Moreno等在文献[3]中提出了一种研究BA无标度网络的相继故障模型,该模型是负荷-容量模型中的一种。他们利用Weibull分布,赋予网络中每个节点一个安全阈值,并且假设每个节点承担相同的负荷,一旦某个节点的负荷超出其阈值则说明该节点发生了故障。而Motter等在文献[10]中提出并研究了另一种模型,也就是最经典的ML负荷模型。ML模型规定:对于一个给定的具有N个节点的网络,如果信息或能量总是在节点对之间沿着最短路径交换,那么定义节点的负荷为该节点的介数,它反映了网络中通过该节点的最短路径的数目。同时,定义节点容量与节点负荷呈线性关系。一旦节点负荷超过其自身容量,则该节点发生故障。文献[11-12]在负荷-容量模型的基础上对小世界网络和无标度网络的相继故障传播机制进行了研究,得出无标度网络对随机节点故障具有较高的鲁棒性,但是对蓄意攻击表现出高度的脆弱性。这表明相继故障的传播机制针对不同的网络模型所表现出的特性是不一样的。
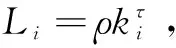
文中提出基于节点最大剩余容量的负荷再分配策略,其实质也是一种全局负荷再分配策略。与以往的全局负荷再分配策略相比,当网络中某一节点出现故障,故障节点的负荷不再分配给网络内所有处于正常状态的节点,而是选择处于正常状态节点中剩余容量最大的部分节点进行分配。这样做的好处在于:以往的全局负荷再分配策略在网络出现故障后,选择所有处于正常状态的节点作为可分配节点,但是这些节点中有些节点的负荷已经近乎满容量。对于这部分节点它们已经没有足够大的剩余容量来处理所分得的负荷,这样并不利于网络鲁棒性的提高。另一方面,举电力网为例,把电能从一个地点输送到另一个地点是会存在电能损耗的,对应到网络模型中这部分损耗实际上是节点之间分配负荷所需的成本。显然,文中所提出的负荷再分配策略选择剩余容量最大的部分节点作为可分配节点,相比于以往的全局再分配策略,可分配节点个数变小,分配成本更低。
2 负荷再分配策略
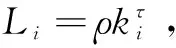
假设网络中节点i发生故障,节点j是当前时刻网络内剩余容量最大的部分节点之一。定义节点j能从节点i处分得的负荷占故障节点i的负荷比例为pij:
(1)
其中,Cj-Lj表示节点j的剩余容量;ki表示节点i的度;Γki表示当节点i发生故障时网络内剩余容量最大的前ki个节点所组成的集合,节点j∈Γki。
在节点i发生故障后,之所以选择前ki个剩余容量最大的节点作为可分配节点,是因为网络中度的大小通常是表示一个节点重要性的指标,直观上看,一个节点的度越大意味着这个节点在某种意义上越“重要”。所以度越大的节点发生故障时,影响的节点个数应该越多,也就是故障节点选择的可分配节点个数越多。相反,一个节点的度越小,影响的节点个数也越小,选择的可分配节点个数越少。
节点j所能分得的负荷ΔLij为:
ΔLij=Lipij
(2)
(3)
此时节点j的负荷更新为:
Lj←Lj+ΔLij
(4)
当Lj>Cj,说明节点j所获得的负荷已经超过其容量,则网络的相继故障开始触发。基于节点最大剩余容量的负荷再分配策略由于在每次节点发生故障时,都是选择网络内剩余容量最大的部分节点,尽可能实现了负载均衡,所以能很好地提高网络的鲁棒性。
3 仿真分析
根据文中所提出的负荷再分配策略,主要在BA网络和WS小世界两种人工网络上做了仿真研究。同时也在美国电力网络的网络拓扑上进行了研究。其中BA网络从一个具有m0个节点的全连通网络开始构造,每次引入一个新的节点连接到m个已经存在的节点上,网络的最终节点个数为N。选取网络节点个数N为500的BA网络作为研究对象,其中BA1的初始节点数m0和连接节点数m都为3,BA2的初始节点数和连接节点数m都为4。
仿真过程中采用最大度攻击方式[17],即攻击网络中度最大的节点。同时利用网络故障率bn[3]来量化攻击网络后网络的故障规模。取ρ=1,τ=1.6,仿真过程中的网络拓扑结构为邻接矩阵A,aij为A中元素,若节点i和节点j之间有连边,则aij=1,反之aij=0,网络中不考虑自环的存在。分别对全局负荷再分配策略(GRS)和基于节点最大剩余容量的负荷再分配策略(BMRS)进行了仿真,如图1和图2所示。
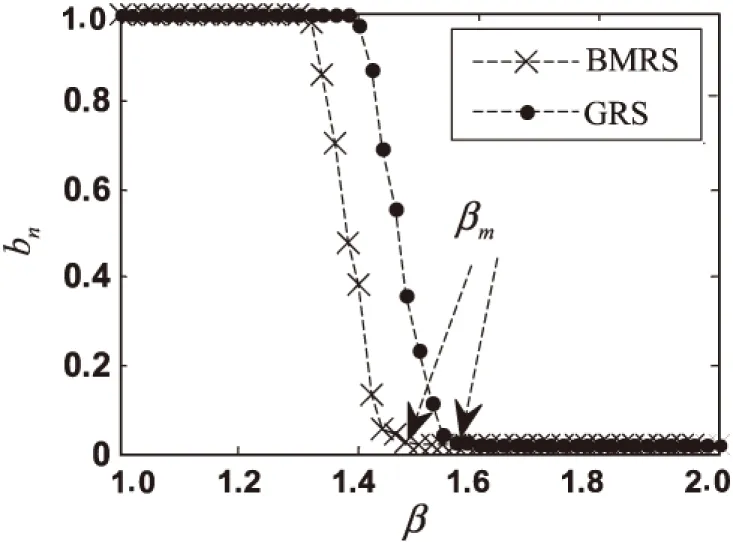
图1 β与bn的关系图(BA1)
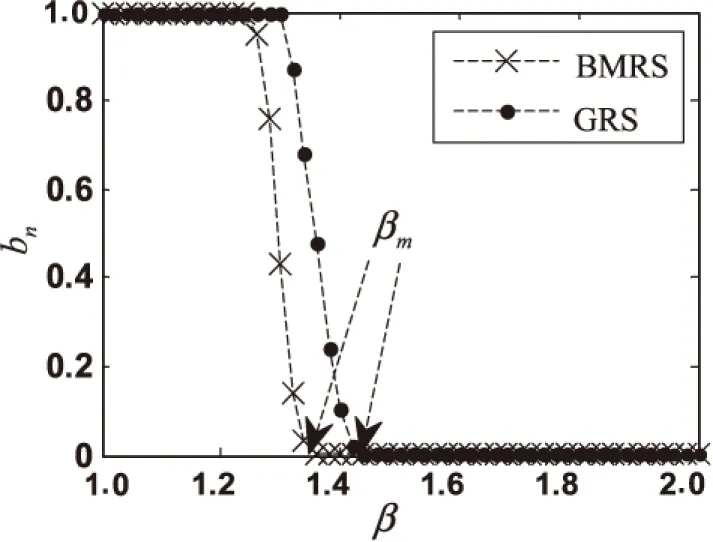
图2 β与bn的关系图(BA2)
以上仿真图表示在两种分配策略下,攻击不同的BA网络得到的β值和网络故障率bn的关系。其中,β代表节点初始负荷和节点容量的倍数关系;网络故障率bn是指网络发生相继故障之后,失效节点个数与原网络节点个数的比值。
分析以上的仿真图,β从1开始增大,两种分配方式下的网络故障率bn一开始都为1,表明网络在受到攻击后,所有节点都发生了故障,网络中并不存在连通子图,也就是说整个网络已经崩溃。这是因为β的值还不够大,节点的剩余容量比较小,节点不具备处理额外负荷的能力。可以这么理解,一个网络虽然处于正常状态,但是它的每个节点的负荷已经近乎满容量,那么该网络在受到攻击以后很容易会使整个网络发生崩溃。随着β的增大,两种分配方式下的bn都会在β达到一个定值后从1开始减小,这表明网络在遭受攻击以后,不会使整个网络发生崩溃,网络中存在连通子图,表明此时网络内部节点已经可以处理部分额外负荷。而当bn达到最小值,此时的β所对应的值为βm。表明网络遭受攻击以后,只有遭受攻击的节点,或者极少部分的节点会从网络中断开成为失效节点,而并不会引起网络大规模的相继故障,说明此时网络已经完全有能力处理额外负荷。当β≥βm,由于网络中每个节点都有能力来处理额外负荷,bn不变,相继故障将不会出现在网络中,显然βm是网络避免相继故障出现的一个重要指标。βm被称为临界阈值[15],在一些实际网络里βm和网络的设计成本呈正相关的关系。βm越小,网络的设计成本越低,网络鲁棒性越强。
通过仿真得到,在网络BA1中,由BMRS得到的βm为1.50,由GRS得到的βm为1.61。在网络BA2中,由BMRS得到的βm为1.36,由GRS得到的βm为1.44。这说明同一个网络受到攻击时,采用BMRS相比于GRS所能得到的临界阈值更小。说明文中所提出的负荷再分配策略能有效减小网络的临界阈值βm,提高网络鲁棒性。
对小世界网络也进行了仿真。在构造WS小世界网络时,初始时刻的网络模型是最近邻耦合网络,网络中的每个节点与左右相邻的各K/2个节点相连,p为重连概率。这里同样选取节点个数N为500的WS小世界网络作为研究对象。其中,WS1的初始K值为4,WS2的初始K值为6,所有WS小世界网络的重连概率p都为0.01。采用最大度攻击方式,仿真结果如图3和图4所示。
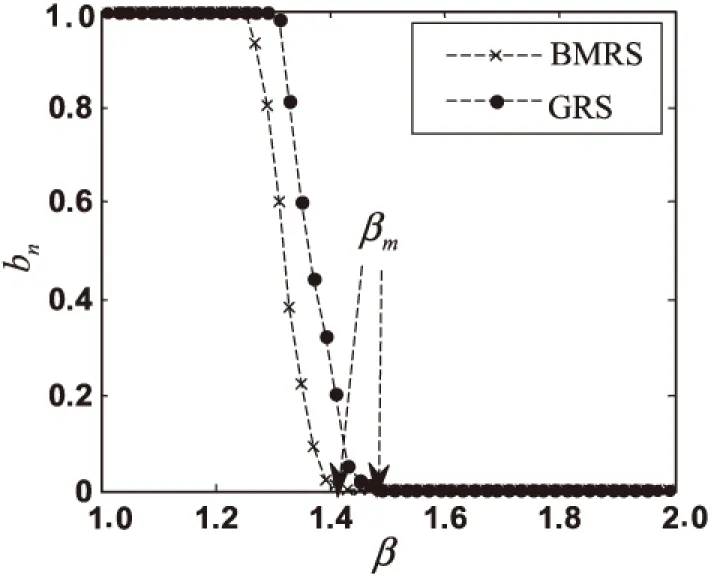
图3 β与bn的关系图
在网络WS1中,由BMRS得到βm为1.43,由GRS得到的βm为1.49。在网络WS2中,由BMRS得到的βm为1.23,由GRS得到的βm为1.33。可以发现BMRS能有效减小临界阈值,仿真结果与BA网络的情况相同。
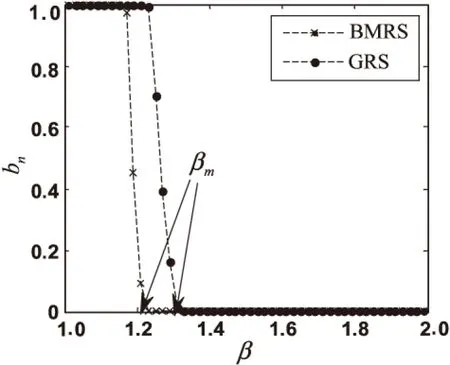
图4 β与bn的关系图(WS2)
为了使结论更具说服力,又选用了美国电力网的网络拓扑进行了仿真。该网络拓扑的节点个数为4 941,边数为6 594,平均度为2.67,仿真结果如图5所示。
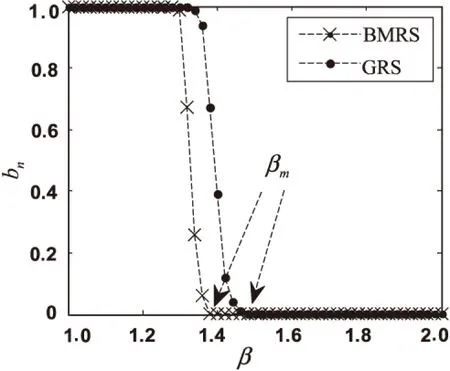
图5 美国电力网β和bn的关系
同样得到了和人工网络中相同的结论,BMRS能够减小临界阈值、提高网络鲁棒性。
4 结束语
文中提出了基于节点最大剩余容量的负荷再分配策略,相比于以往的全局负荷再分配策略,选择当前时刻剩余容量最大的部分节点作为可分配节点,减少了可分配节点的数量,降低了分配成本。同时由仿真可得,该策略也减小了临界阈值βm,提高了网络鲁棒性。与全局负荷再分配策略相比有其优越性。
然而文中的研究主要针对的是BA无标度网络、WS小世界网络以及美国电力网,并没有对更多的网络模型作深入探讨。在基于节点最大剩余容量的负荷再分配方式下,网络平均路径长度的增大会不会对临界阈值有显著影响,如果有影响又会是一种怎样的方式,这种分配方式运用到其他的实际网络模型中又有哪些不足,这些都是后续要进一步研究的内容。
[1]AlbertR,AlbertI,NakaradoGL.StructuralvulnerabilityoftheNorthAmericanpowergrid[J].PhysicalReviewE,2004,69(2):025103.
[2]StrogatzSH.Exploringcomplexnetworks[J].Nature,2001,410(6825):268-276.
[3]MorenoY,GómezJB,PachecoAF.Instabilityofscale-freenetworksundernode-breakingavalanches[J].EPL,2002,58(4):630.
[4]DobsonI,CarrerasBA,LynchVE,etal.Complexsystemsanalysisofseriesofblackouts:cascadingfailure,criticality,andself-organization[J].BulkPowerSystemDynamicsandControl-VI,Cortinad’AmpezzoItaly,2002,17(2):438-451.
[5]WattsDJ.Asimplemodelofglobalcascadesonrandomnetworks[J].ProceedingsoftheNationalAcademyofSciencesoftheUnitedStatesofAmerica,2002,99(9):5766-5771.
[6]DobsonI,ChenJ,ThorpJS,etal.Examiningcriticalityofblackoutsinpowersystemmodelswithcascadingevents[C]//Proceedingsof35thHawaiiinternationalconferenceonsystemsciences.Hawaii:[s.n.],2002:63-72.
[7]GohKI,LeeDS,KahngB,etal.Sandpileonscale-freenetworks[J].PhysicalReviewLetters,2003,91(14):148701.
[8]DobsonI,CarrerasBA,NewmanDE.Aprobabilisticloading-dependentmodelofcascadingfailureandpossibleimplicationsforblackouts[C]//Proceedingsof35thHawaiiinternationalconferenceonsystemsciences.Hawaii:[s.n.],2003:1-8.
[9]WangXF,XuJ.Cascadingfailuresincoupledmaplattices[J].PhysicalReviewE,2004,70(5):056113.
[10]MotterAE,LaiYC.Cascade-basedattacksoncomplexnetworks[J].PhysicalReviewE,2003,66(6):114-129.
[11]ZhaoL,ParkK,LaiYC.Attackvulnerabilityofscale-freenetworksduetocascadingbreakdown[J].PhysicalReviewE,2004,70(3):035101.
[12]ZhaoL,ParkK,LaiYC,etal.Toleranceofscale-freenetworksagainstattack-inducedcascades[J].PhysicalReviewEStatisticalNonlinear&SoftMatterPhysics,2005,72(2):025104.
[13]XiaY,FanJ,HillD.CascadingfailureinWatts-Strogatzsmall-worldnetworks[J].PhysicaA:StatisticalMechanics&ItsApplications,2010,389(6):1281-1285.
[14]WangWX,ChenG.Universalrobustnesscharacteristicofweightednetworksagainstcascadingfailure[J].PhysicalReviewE,2008,77(2):026101.
[15]WangJ,RongL,ZhangL.Amodelforcascadingfailuresincomplexnetworkswithatunableparameter[J].ModernPhysicsLettersB,2009,23(10):1323-1332.
[16]DuanDL,LingXD,WuXY,etal.Criticalthresholdsforscale-freenetworksagainstcascadingfailures[J].PhysicaA:StatisticalMechanics&ItsApplications,2014,416:252-258.
[17]AlbertR,JeongH,BarabásiAL.Errorandattacktoleranceofcomplexnetworks[J].Nature,2000,406(6794):378-382.
Research on Load Redistribution Strategy Based on Maximum Remaining Capacity of Node
ZHOU Tian-jie,JIANG Guo-ping
(School of Automation,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)
In order to improve the network robustness in the process of cascading failure,a reasonable and effective load redistribution strategy of the cascading failure nodes in the network is designed,so that the critical thresholdβmcanbedecreased.Throughcomparativestudyandsimulationmodelingmethod,aloadredistributionstrategybasedonthemaximumremainingcapacityofthenodeisputforward.Theloadofafailurenodewillbedistributedtothenodesthathavethemaximumremainingcapacityinthenetwork,andthenumberofthesenodesisthedegreeofthefaultnode,andtheextraloadwhichthesenodessharedependsontheirremainingcapacity.Throughthesimulationbetweentheartificialnetworkandactualnetwork,theresultsshowthattheproposedstrategyoftheloadredistributioncaneffectivelydecreasethecriticalthresholdβm,soastoshowtheeffectivenessofthestrategyandimprovetherobustnessofthenetwork.
complex networks;cascading failures;load redistribution;network robustness
2016-01-20
2016-05-11
时间:2016-10-24
国家自然科学基金资助项目(61374180)
周添杰(1990-),男,硕士研究生,研究方向为复杂系统和网络控制;蒋国平,教授,博士生导师,研究方向为混沌系统同步与控制、混沌信息处理与混沌通信系统设计、复杂网络理论。
http://www.cnki.net/kcms/detail/61.1450.TP.20161024.1113.034.html
TP
A
1673-629X(2016)11-0063-04
10.3969/j.issn.1673-629X.2016.11.014
