改进的SIFT图像匹配算法
2016-02-27翟社平
李 炀,翟社平
(西安邮电大学 计算机学院,陕西 西安 710061)
改进的SIFT图像匹配算法
李 炀,翟社平
(西安邮电大学 计算机学院,陕西 西安 710061)
在众多图像匹配算法中,SIFT算法是在总结了众多传统算法优势的基础上,将尺度空间理论融合到图像特征点提取过程中,这样SIFT算法就保持了图像的尺度和旋转不变性,另外在外部光照变化等因素的影响下也能对图像的特征点进行准确的匹配,但该算法在仿射变换方面还存在很大的不足。针对不足之处,采用SIFT算法的方法提取图像的特征点,然后通过使用ASIFT中的方法对提取到的特征点进行仿射变换以及为特征点分配方向,这样在增强了图像的抗仿射性的基础上也保持了图像的旋转不变性。实验结果表明,改进算法在保持了原SIFT算法各种优势的基础上,在增强图像的抗仿射性方面,可以取得良好的效果。
SIFT;ASIFT;抗仿射性;图像匹配;特征点
0 引 言
随着计算机技术的发展,人工智能、机器视觉等人机交互技术也成为科研工作者重点研究的方向。研究人机交互技术时有一项关键技术就是图像匹配。
1999年哥伦比亚大学的David G.Lowe教授[1]总结了现有的基于不变量技术的特征检测方法,并正式提出了一种基于尺度空间,对图像旋转、缩放以及仿射变换保持不变性的局部图像特征描述算法—SIFT(尺度不变特征变换),并且该算法在2004年被Lowe教授完善。
SIFT算法虽然对图像的旋转、缩放以及仿射变换保持不变性,但是在图像发生较大的仿射变换时该算法的匹配效果将会大大下降,并且由于它生成的描述子为128维,这给后续的图像匹配增加了负担和计算复杂度。于是Ye等提出的PCA-SIFT[2]算法就是在SIFT算法的基础上对其进行降维,减少了匹配过程的计算量,但是这使得匹配率有所下降。无论是SIFT还是PCA-SIFT都得将图像转换成灰度图像才能进行处理,CSIFT[3]算法是针对彩色图像进行不变特征的提取。SURF[4]算法可以说是SIFT算法的加强版,其计算量小,运算速度快,而且提取的特征点数量几乎与SIFT相同,但同样它也继承了SIFT的一个陋习,就是在图像发生较大的仿射变换时,图像的匹配效果将大打折扣。由于SIFT和SURF不具有完全仿射不变性,因此J.M.Morel等提出了ASIFT[5]算法,该算法可以抵抗强仿射变换,增加了提取的特征点数量,但是唯一的缺点是计算量过大,不能满足实时性要求。
基于SIFT算法与ASIFT算法的优势,文中提出将ASIFT算法中抗仿射性的方法与SIFT算法相结合,既解决了ASIFT算法计算量大的问题,又解决了SIFT算法抗仿射性差的问题。
1 SIFT算法
SIFT算法是Lowe教授在1999年对之前的图像匹配算法总结的基础上提出的,并在2004年进行了完善。SIFT(Scale Invariant Feature Transform,尺度不变特征变换)是基于局部特征描述的算子,就是对图像中的局部区域进行不变量的提取。该算法是在尺度空间[6]对关键点进行提取,然后将提取到的关键点进行方向描述,这样就可以保持尺度和旋转不变性,最后生成一个特征点描述子。
SIFT算法对图像中的关键点进行提取时,是对图像中一些不变性比较好的点进行提取。不变性好的点就是一些十分突出的点,不会由于噪声和光照等外界因素的变化而变化,比如在一片黑色区域中的亮点、角点、边缘点等。SIFT算法的实现主要包括四个步骤:
(1)尺度空间极值点提取;
(2)关键点精确定位;
(3)关键点方向分配;
(4)生成关键点描述子。
通过这四个步骤提取整幅图像中的特征点,之后做图像匹配时,只需比较两幅图像中的特征点的相似度就可以判断这两幅图像的相似程度了。
虽说SIFT算法在图像匹配时具有很大的优势,但当一幅图像发生较大的仿射变换时,SIFT算法的匹配效果将会大大下降。
2 SIFT算法的改进
文中算法在SIFT算法的基础上进行改进,主要是对SIFT算法的抗仿射能力进行了改善。主要包括以下几个步骤:
(1)尺度空间极值点提取;
(2)关键点精确定位;
(3)对关键点进行仿射模拟;
(4)为关键点分配方向;
(5)生成特征点描述子。
2.1 尺度空间极值点提取
SIFT算法首先通过对图像做高斯模糊和降采样来构建高斯金字塔,这样一幅图像就可以产生几组图像,在每一组图像中又可以分成几层(一般为3~5层)。然后对每组图像进行高斯差分处理,在处理后的图像中提取极值点。
高斯核是实现尺度变换的唯一线性变换核[7],因此尺度函数空间L(x,y,σ)是由图像函数I(x,y)与高斯函数卷积得到。
L(x,y,σ)=I(x,y)*G(x,y,σ)
(1)
(2)
通过改变σ的值将得到一些列的高斯模糊后的图像,这些图像便构成了尺度空间。然后对尺度空间里面的每组图片进行分层,并将每组图片的最高一层进行高斯模糊。接下来对相邻两层做差及高斯差分处理,这一处理通过高斯差分函数D(x,y,σ)实现。
D(x,y,σ)=L(x,y,kσ)-L(x,y,σ)
(3)
得到高斯差分尺度空间后,在高斯差分尺度空间中将每个像素点与它同尺度的8个像素以及上下相邻尺度的18个像素点作比较,最后找到局部区域的极值点。
2.2 关键点精确定位
由于高斯差分函数对噪声比较敏感,会对提取到的极值点的准确性产生一定影响,因此还需要对提取到的极值点继续进行检测。为了提高关键点的稳定性,需要对提取到的极值点进行曲线拟合。利用高斯差分函数在尺度空间的泰勒展开式为:
(4)
得到的极值点为:
(5)
将极值点带入式(4)中得到极值为:
(6)
Lowe教授指出,重复以上步骤5次得到的效果较好,然后去除那些效果不好的极值点。将式(6)中绝对值小于等于0.02的极值点去除。
以上仅仅去除了对比度较低的极值点,高斯差分函数还具有很强的边缘响应。也就是高斯差分函数的峰值点在横跨边缘的方向有较大的主曲率[8],垂直边缘有较小的主曲率。而主曲率可以通过计算该点的二阶Hessian得到:
(7)
其中,Dxx表示高斯差分金字塔中某尺度在x方向求二阶导。这里D的主曲率与H的特征值成正比,为了避免计算特征值而只考虑它们之间的比例关系。令α为最大特征值,β为最小特征值,则它们之间的关系设为α=rβ。
Tr(H)=Dxx+Dyy=α+β
(8)
Det(H)=DxxDyy-(Dxy)2
(9)
因此D的主曲率与H的特征值的比例关系如下:
(10)
Lowe教授在他的论文中指出,当这一比例关系不在某阈值范围内时则将该点删除。
2.3 对关键点进行仿射模拟
ASIFT算法加入经度和纬度是为了构建仿射空间,然后在仿射空间中对待匹配的图像进行仿射模拟,进而对模拟的图像进行匹配,这样就保证了图像的仿射不变性。这样做是将整幅图片中的所有像素点都进行仿射空间的构建,将会增加计算量,进而导致算法运行速度下降。而文中算法是仅仅对图片中的特征点进行仿射变换,相较于整幅图片来说,特征点的数量仅仅占很小的一部分,因此计算量将会下降。
其行列式为正,且不存在相似矩阵,则其存在唯一的分解[9]:
(11)
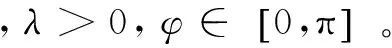
仿射空间的构建方法如下:
(12)
其中,I'为特征点的集合。
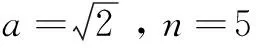
2.4 关键点分配方向
为了保证提取到的特征点的旋转不变性,还需要为关键点指定方向参数,这样就可以保证在图片发生旋转后仍然能够提取关键点并与原图像中的点匹配。为关键点赋予方向采用求每个点梯度值的方法。
像素的梯度表示如下:
(13)
梯度幅值为:
m(x,y)=(L(x+1,y)-L(x-1,y))2+(L(x,y+1)-L(x,y-1))1/2
(14)
梯度方向为:
(15)
确定关键点的方向采用梯度直方图的统计法,如图1所示,统计以关键点为中心一定区域内的图像像素点对关键点方向所做的贡献。
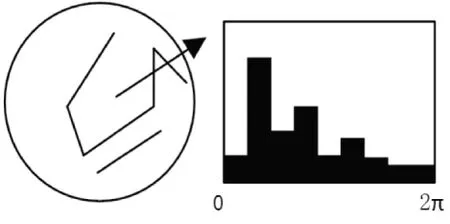
图1 梯度直方图
直方图以每10°方向为一个柱,共36个柱,柱所代表的方向为像素点的方向,柱的长度代表了梯度幅值[10]。Lowe教授建议直方图半径采用3*1.5*σ。直方图进行统计时,每相邻三个点要采用高斯加权,模板采用[0.25,0.5,0.25],并连续加权两次,这样就可以为特征点指定方向。
2.5 特征点描述
以关键点为中心取16×16的窗口,在每4×4的小块上计算8个方向的梯度方向直方图,绘制每个梯度方向的累加值,即可形成一个种子点,这样一个关键点由4×4共16个种子点组成,每个种子点有8个方向向量信息,形成128维的SIFT特征向量[11]。
如图2所示,左图的种子点由8×8单元组成,每一个小格都代表了特征点邻域所在的尺度空间的一个像素,箭头方向代表了像素梯度方向,箭头长度代表该像素的幅值。然后在4×4的窗口内计算8个方向的梯度方向直方图。绘制每个梯度方向的累加可形成一个种子点,右图为一个特征点由4个种子点的信息组成。
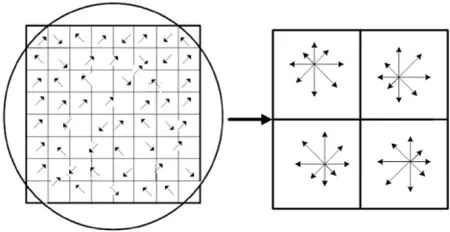
图2 描述子生成示意图
对生成的128维向量描述子与带匹配的图像的描述子进行欧氏距离[12]计算,就可以得到两张图像的相似度。
2.6 算法描述
以下用伪代码对文中算法进行描述:
I=read(image)
//得到图像的信息,x:长,y:宽
f(x,y)=getInformat(I)
//得到髙斯金字塔的层数
m=min(x,y)
//高斯金字塔中每一层的组数,一般为3~5
M=3
//构建高斯金字塔
GaussianIM(image)
{
for i=0 to m
{//对图像做高斯模糊处理
A(i)=Gaussian(I)
for j=0 to M+3
{//对每一层的图像做高斯处理,得到6组图像
B(j)=Gaussian(A(i)) j=j+1
}
//对图像做降采样处理
DownSample(A(image))
i=i+1
}
}
//求高斯金字塔中的极值像素点
extreme(image)
{//对高斯金字塔做高斯差分处理
DOGIM(GaussianIM(image))
//每一组图像在尺度空间中的极值点
getextreme(DOGIM)}
exactpoint()
{
//消除极值点中的边缘相应
I1(x,y)=Dealedge(extreme(image))
//使用泰勒公式对离散的极值点做进一步处理
I2(x,y)=Taylor(I1)
//对求得的极值点进行仿射空间的模拟
AffineDeal(exactpoint)
//为每个极值点分配方向,使其具有方向性
distribute(I2)
}
//对仿射空间得到的极值点生成128位的描述子
Descriptor(AffineDeal)
end
3 实验结果与分析
为了验证改进后的算法的正确性,文中分别做了以下两组实验分析及对比。
3.1 匹配率对比
由图3可见,文中算法提升了特征点的匹配率,而且有效降低了ASIFT算法中出现的重复匹配特征点的现象。

图3 实验结果
3.2 匹配时间对比
通过表1可以发现,文中算法相对于ASIFT算法降低了算法运行的时间,并且相对于SIFT算法提升了特征点的匹配率。
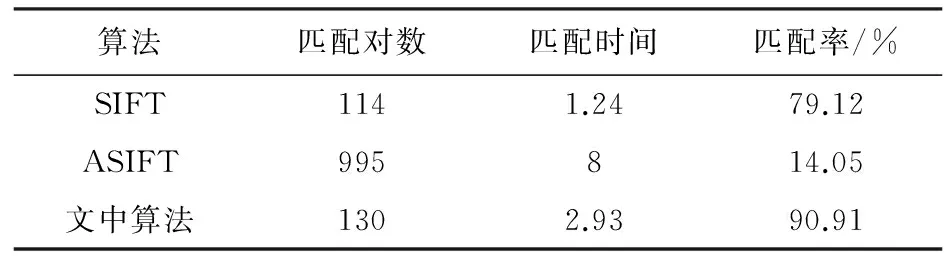
表1 图像实验对比结果
文中算法是在SIFT算法提取特征点的基础上,通过使用ASIFT算法的构造仿射空间的方法,对特征点进行仿射变换,这样将会增强特征点的抗仿射性,同时也降低了计算量。因为文中算法只是针对特征点进行仿射空间的构造,并不是针对图像信息中所有的像素点,相对于整个图像的像素点数量来说,特征点的数量还是比较少,那么计算量将会下降90%以上,同时算法的执行时间也提升了80%以上。实验中,文中算法相对于SIFT算法匹配率提升了11.89%,较ASIFT算法提升了76.86%,并且算法执行速率提升了5.07 s。
文中算法保持了SIFT算法中特征点的尺度、旋转不变性,以及在光照等外部因素影响的条件下,增强了特征点的抗仿射能力,进而增加了图像的匹配率。缺点是在特征点的提取方面保持了与SIFT算法的一致,没有像ASIFT算法那样的特征点提取量。在一些对实时性要求较高的场景,改进算法的效果相对于ASIFT算法将会十分明显。
4 结束语
文中在对SIFT算法和ASIFT算法进行深入研究的基础上,对SIFT算法的抗仿射性能力进行了改进。由于ASIFT是在提取图像特征点之前对图像中的所有像素点构建仿射空间[13-14],也就是进行仿射变换的模拟,这样虽然使得图像特征点的数量得到了提升,但是图像特征点的匹配率却没有提升或提升的效果不明显。通过对SIFT算法特征点提取完成后,对提取到的特征点进行仿射空间的构建,这样就能提升特征点的抗仿射能力,进而提升了特征点的匹配率,同时也降低了在进行仿射空间构建时的计算量,节约了匹配时间,提升了匹配速率。该算法的缺点在于特征点的数量没有ASIFT算法那么多,仅仅是继承了SIFT算法的特征点数量,所以还值得深入研究。
[1] Lowe D G.Distinctive image features from scale-invariant key-point[J].International Journal of Computer Vision,2004,60(2):91-110.
[2] Ye K,Sukthankar R.PCA-SIFT:a more distinctive representation for local image descriptors[C]//Proceedings of the conference on computer vision and pattern recognition.[s.l.]:IEEE,2004:90-98.
[3] Abdel-Hakim A E,Farag A A.CSIFT:ASIFT descriptor with color invariant characteristics[C]//IEEE computer society conference on computer vision and pattern recognition.[s.l.]:IEEE,2006:1978-1983.
[4] Bay H,Ess A,Tuytelars T,et al.Speeded-Up Robust Features(SURF)[J].Computer Vision and Image Understanding,2008,110(3):346-359.
[5] Morel J M,Yu Guoshen.ASIFT:a new framework for fully affine invariant image comparison[J].SIAM Journal on Imaging Sciences,2009,2(2):438-469.
[6] Lindeberg T. Scale-space theory:a basic tool for analysing structures at different scales[J].Journal of Applied Statistics,1994,21(2):223-261.
[7] Lindeberg T.Scale-space theory in computer vision[M].[s.l.]:Springer Science & Business Media,1994.
[8] Babaud J,Witkin A P,Baudin M,et al.Uniqueness of the Gaussian kernel for scale-space filtering[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1986,8(1):26-33.
[9] 卢 彬.改进的ASIFT算法在图像配准中的应用[J].电视技术,2014,38(11):211-214.
[10] 周 颖.基于SIFT算法的图像特征匹配[J].现代计算机,2015(2):63-68.
[11] 朱 进,丁亚洲,肖雄武,等.基于SIFT改进算法的大幅面无人机影像特征匹配方法[J].计算机应用研究,2015,32(10):3156-3159.
[12] 张忠林,曹志宇,李元韬.基于加权欧式距离的k_means算法研究[J].郑州大学学报:工学版,2010,31(1):89-92.
[13] 何婷婷,芮建武,温 腊.CPU-GPU协同算加速ASIFT算法[J].计算机科学,2014,41(5):14-19.
[14] 宋耀鑫,张丹丹,唐伶俐,等.基于ASIFT算法的低重叠度无人机影像拼接方法[J].遥感技术与应用,2015,30(4):725-730.
Improved SIFT Image Matching Algorithm
LI Yang,ZHAI She-ping
(School of Computer Science,Xi’an University of Posts and Telecommunications,Xi’an 710061,China)
In many image matching algorithm,SIFT algorithm puts the scale space theory fusion into image feature point extraction process based on the summary of the advantages of many traditional algorithms,so that it keeps the scale and rotation invariance for image and in the external light illumination changes and other factors influence,can also match the image feature points accurately.But it still exists great shortage in terms of affine transformation.Aiming at them,the SIFT method is used to extract image feature points and ASIFT method is applied to carry out affine transformation for extracted feature points and to distribute direction,enhancing image anti affine and maintaining the image rotation invariance.The experimental results show that the improved algorithm can achieve good results in enhancing the anti radiation of the image based on the advantages of the original SIFT algorithm.
SIFT;ASIFT;anti affine;image matching;feature points
2016-01-25
2016-05-11
时间:2016-10-24
陕西省自然基金面上项目(2012JM8044);陕西省教育厅项目(12JK0733);西安邮电大学创新基金项目(114-602080059)
李 炀(1990-),男,硕士,研究方向为嵌入式系统设计;翟社平,副教授,博士,研究方向为嵌入式系统、语义Web。
http://www.cnki.net/kcms/detail/61.1450.TP.20161024.1114.052.html
TP391.41
A
1673-629X(2016)11-0058-05
10.3969/j.issn.1673-629X.2016.11.013
