基于分段可调节OMP算法的图像压缩感知算法
2016-02-27石曼曼
石曼曼,李 雷
(南京邮电大学 理学院,江苏 南京 210023)
基于分段可调节OMP算法的图像压缩感知算法
石曼曼,李 雷
(南京邮电大学 理学院,江苏 南京 210023)
压缩感知(CS)理论作用在稀疏信号或可压缩信号,用很小的采样速率,保证信号采样与压缩同时进行,并可以精确恢复原始信号。文中侧重CS重构算法中经典的贪婪算法研究,介绍了四种经典的贪婪算法:正交匹配(OMP)算法、正则化正交匹配(ROMP)算法、压缩采样匹配追踪(CoSaMP)算法和分段正交匹配追踪(StOMP)算法。从重构精度和重构耗时两个方面,结合横向和纵向详细的比较,详尽地给出了不同算法的区别以及优缺点。在StOMP算法增加考虑稀疏度和观测矩阵行列关系的可调节因子,提出了一种改进算法—分段可调节OMP重构(StrOMP)算法。通过仿真实验发现,提出的改进算法既提高了图像重构精度,又保证了其重构时间短的优越性。
压缩感知;贪婪算法;图像重构;分段可调节正交匹配追踪算法
1 概 述
通过传统奈奎斯特采样定理可知,要精准恢复出原始信号,其采样速率至少要大于信号两倍频宽。而压缩感知(Compressed Sensing,CS)[1-2]有效地解决了传统奈奎斯特定理采样数据时的带宽限制,减少了采样端硬件元件损耗,因此在信息处理领域应用广泛。
CS理论包括信号稀疏表示、观测矩阵设计和信号重构三个关键问题。它指出,在某一变换域上,若信号是稀疏的或是可压缩的,便可用一个与变换基不相关的观测矩阵将变换所得的高维信号投影至低维空间,并保持重建所需的信息,通过求解一个优化问题,便能从少量投影中高概率重构出原始信号。
(1)
x=Ψθ
(2)
其中,Ψ=[Ψ1,Ψ2,…,ΨN]∈RN×N为正交基字典矩阵,并且ΨΨT=ΨTΨ=I;系数向量Θ=[θ1,θ2,…,θN]T。
假设θ里K≪N,也就是向量θ是K-稀疏的,使用一个随机测量阵Φ:M×N(M≪N),且这个矩阵与正交基字典X不相干,于是对x做如下投影:
y=Φx
(3)
能够得到M个线性观测(或称线性投影)y∈RM,而这些线性投影拥有足够多的信息来恢复出信号x。注意Φ的每行跟θ做乘法以后,就会获得x的局部信息。
从观测y还原出信号x,就转化成一个求线性方程组解的问题,但是由于观测y∈RM是M维的,远小于N,没有唯一解。考虑把式(2)代入式(3),记CS信息算子ACS=ΦΨ,能够得到:
y=ΦΨθ=ACSθ
(4)
虽说从观测y还原θ仍是一个欠定问题,可是注意到θ具有稀疏性,于是信号极有可能被恢复出来。能够验证的是:如果ACS里任意2K列均符合独立这个条件,就至少有某个θ符合y=ACSθ,且θ是K-稀疏。也就是解一个非线性优化问题来精准重构出原始信号x。
2 基于CS的信息重建算法
2.1 正交匹配追踪(OMP)类算法
OMP类算法作为贪婪算法的主流算法被广泛应用。本节对OMP算法[3]、ROMP算法[4]、CoSaMP算法[5]和StOMP算法[6]进行研究分析,并给出四种重建算法的重构效果。该类算法是通过贪心思想,使得每迭代一步得到一个局部最优解,逐步逼近原信号。这四种算法的共同点都是利用MP算法中的原子选择原则,选取原子更新支撑集,然后利用最小二乘法取得最优解[7]。四种算法的区别是原子的选择方式不同。
对于OMP算法,其本质思想是:凭迭代更新找出投影矩阵Φ的列,然后更新寻求的列和当前冗余向量最相关,之后把相干原子从Φ里面剔除,更新K次。而ROMP算法依照相关性原则对原子做第一次选择,取出K个相应的索引值放进指标集合J中;依照正则性再次挑选,原则如下:
ui≤2uj,i,j∈J
(5)

2.2 OMP类算法仿真实验与分析
CS重构过程中,文中使用离散小波变换形成DWT基对图像做稀疏化变换,然后选取随机高斯矩阵[8-9]对图像取得观测值,最后用贪婪算法对观测值做重建操作。实验对象为图像库中的Lena图像(512*512,jpg),稀疏度的估计取经验值K=M/(2*lg(N))。用PSNR(dB)值来判断算法重建效果的好坏,值愈大愈好;用重建耗时(s)值来判断恢复速度,值愈小愈好。
以下不同算法的仿真实验均采用相同的运行平台和衡量指标,采样率均为0.2。每个算法做5次MATLAB仿真,以平均结果作为最终算法的PSNR与重建耗时值。仿真结果如图1所示。

图1 原始图像及四种算法重构效果图
从图1可以看到,四种算法均能完成实验仿真。给出图像在不同采样率下的PSNR值(dB)与重构消耗时间t值(s),见表1和表2。

表1 OMP类算法Lena重建PSNR变化表
从表1和表2中可以看到,贪婪算法在图像重构应用[10-13]中,除StOMP算法外,其余算法均随采样率的增加,PSNR值增加,耗时增大,这表明重构效果越来越好,但与之相对应的是消耗时间变长,但能够较好地恢复出原始图像;而StOMP算法下的重构是随采样率增大,PSNR值变小,耗时增加,这与阈值的选择有关。

表2 OMP类算法Lena重建耗时t变化表
ROMP算法好于OMP算法,在相同条件下重构效果好且重构时间短。ROMP在采样率M/N等于0.4、0.5时,可以较为准确地重建出原来的图像。采样率相同时,CoSaMP算法重建出的PSNR值要略高于ROMP和OMP算法,重建效果好,重建耗时远大于前两种算法。StOMP算法加入了阈值,设定了迭代次数,在一定程度上简化了OMP算法,能明显看出重构耗时之少,但只有保证准确预测出K,才会精准恢复出原信号。阈值的选择问题对于重构效果非常关键,至于究竟该选多大的阈值,则要根据实际情况在具体的实践应用中进行选择,一般阈值取值范围为2≤ζ≤3。所以在StOMP算法上,阈值的选择也是一个须要探究的方向。
3 基于分段可调节(StrOMP)算法在图像上的运用
贪婪算法的运行速度是相当快的,不同的算法会产生不一样的重构效果,一般来说对于重建精度比较高的算法,重建耗时会相对增多;重建出的信息精度较低的算法,重建耗时会相对较少,这是由于重构精度和耗时存在不兼容性。基于此,文中对StOMP算法进行改进,寻找一个折中的算法,既能提高其重构精度,又能保证其重构时间少的优越性。
3.1 经典贪婪算法的比较
为体现新算法的优势,需先比较已有的贪婪算法的性能。由于压缩观测时M≪N,那么重建就是求ULE问题解的过程。而结合前述四种算法,给出算法间重建结果的对比,以及重建耗时的比较。图2展现了在采样率M/N等于0.1,0.2,0.3,0.4与0.5的情况下,Lena重建的PSNR值和重构时间的变化图。
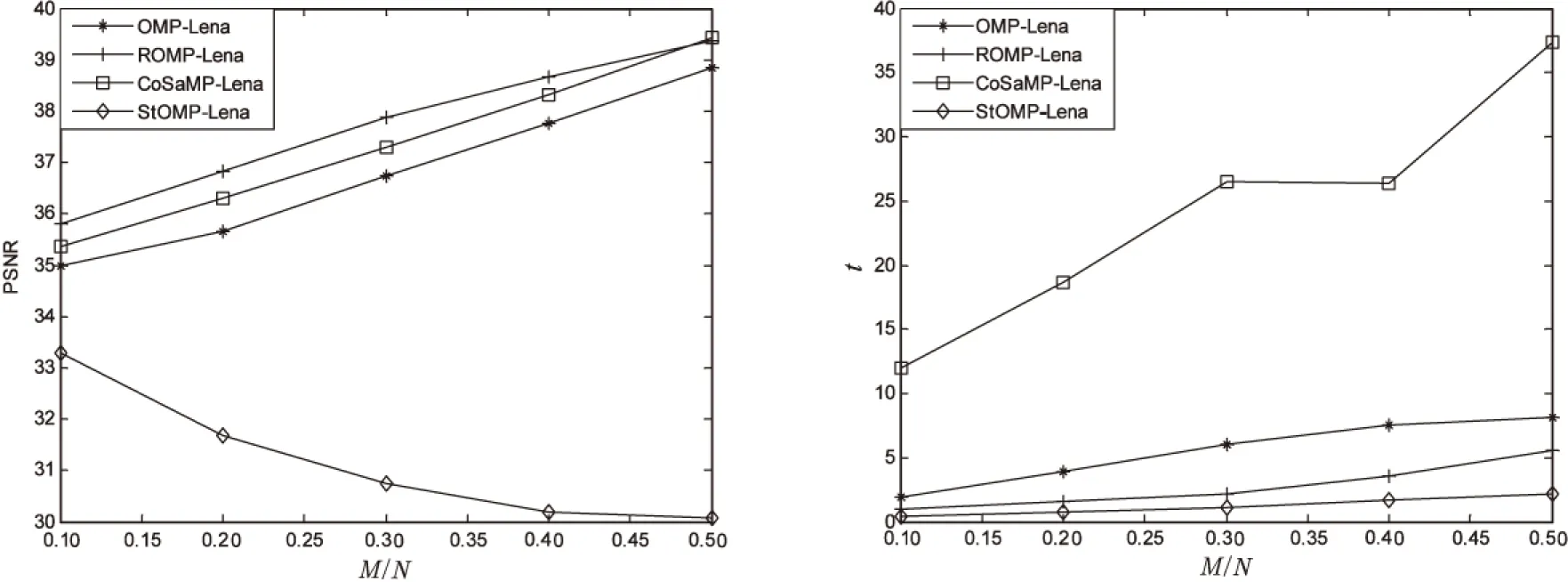
图2 采样率不同时Lena重建PSNR变化图
由图2可知,随着采样率M/N的增加,除StOMP算法的PSNR呈缓慢下降趋势外,其他三种算法均随着采样率的增加而增加,这表明ROMP、CoSaMP同OMP算法相同,随着采样率M/N的增加,重建精度增大,重建效果优,而StOMP算法重建精度却缓慢下降并趋于平稳值。当采样率低于0.5时,ROMP算法的重建结果要稍稍优于CoSaMP,CoSaMP重建结果要优于OMP,OMP又要好过StOMP。即文中给出的四种算法中重建效果最差的当属StOMP。分析信号重构时消耗的时间t,伴随采样率M/N的增大,重建耗时也会跟着增大,而CoSaMP耗时最多,接着为OMP和ROMP算法,耗时最少的则是StOMP算法。这也说明一般情况下,图像重建质量和耗时是不兼容、互相限制的。当PSNR增大时,势必将带来重构耗时的增加;同样,缩短耗时就很可能会牺牲部分重构质量。另外,随着采样率的增加,一般算法的重构精度会变大,重构效率也会有所提高,即重构耗时增加。因此在研究探索新算法时,需要很好地把握这两方面,找到二者的折中点。
3.2 改进的分段可调节OMP(StrOMP)算法
StOMP算法具有很强的可塑性,虽然该算法重构图像质量较差,但具有重构时间极短的优势。在StOMP算法中,一个关键问题就是阈值的选择问题,它会直接关系到重构质量。
StrOMP算法是改进的StOMP算法,设定迭代次数不变,给StOMP算法中的阈值增加一个调节因子,用可调节阈值的办法挑选出原子,与OMP算法的差异在于,它在筛选原子的进程中设立了如下选择标准:
Jk={j|uj>ηtkσk}
(6)

3.3 StrOMP算法步骤
输入:原始信号x∈RN,观测矩阵Φ∈RM×N,观测向量y∈RM,阈值ζ和调节因子η;
核心步骤如下:
(2)计算Cs=ΦTrs-1=<Φ,rs-1>。
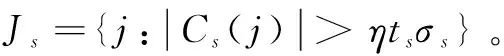

(5)更新残差值:rs=y-Φxs。

StrOMP算法的复杂度没有增加,仅在原阈值上增加了调节因子η。由于采样率不同,导致稀疏度和观测矩阵列的数目发生改变,采样率增大,则M和K也增大,于是考虑其增大的关系,最终给定调节因子为η=M/4.2K,自适应地提高图像重构质量。
4 StrOMP算法仿真结果与性能分析
利用文中提出的StrOMP算法对图像进行重构,重构效果图如图3所示,这里采样率分别取M/N=0.5,0.3,0.1。

图3 StrOMP算法恢复Lena效果图
通过图3可以发现改进的StrOMP算法在采样率不同时能够较为清晰地重构出原始图像,而且可以看到采样率越小,重构效果越好,这跟StOMP算法保持了一致性,说明算法是可以实现的。
为了更加直观地显示StrOMP算法在M/N取不同值时的重建效果以及为了更好地比较两种算法,文中给出Lena图像在不同采样率下的PSNR值(单位:dB)和CS重建部分消耗时间t值(单位:s),见表3。

表3 StrOMP与StOMP算法对Lena重建PSNR和耗时t变化表
从表3中可以看出,StrOMP算法重构PSNR值在相同的采样率下总是略高于StOMP算法,这表明改进算法比原算法重构精度高,重建结果好,虽然改进算法重构时间比原算法略长,但仍然比较迅速。随着采样率的增大,新算法的PSNR值随之减少,而重构耗时却随之变长,这一点与原算法保持一致。主要原因是StrOMP算法没有增加算法的复杂度,仅在阈值的选择方面加入了一个调节因子,但从效果看,文中提出的StrOMP算法在重构精度上优于原来的分段正交匹配追踪算法。
改进算法的重构时间有所增加,但增加值很小,明显优于CoSaMP算法,但是为了比较改进算法在重构时间跟其他算法相比是否仍然具有优势,当采样率不相同时给出OMP、ROMP、StOMP和StrOMP算法对Lena图像重建耗时的变化图及新算法PSNR对比图,见图4。
从图4(a)可以看出,改进后的算法StrOMP除个别点外,随着采样率的增加,重建耗时在随之增加,除采样率为0.3时增加有些快外,其他采样率下均明显优于OMP和ROMP算法,虽然比原算法重构时间略长,但都少于1s,仍然保留了StOMP算法重建快的优点。提出的StrOMP算法也能明显看出计算速度的优势,但由于其仅在阈值选择时加入了调节因子,使得算法的精度略有提高,虽保持了算法的操作简单性,但在所有更新的步骤里挑选的也非最优表示,所以重建精度跟其他算法比较起来不高,效果不是特别好,但是其重构消耗时间短仍是它的优点。

图4 Lena重构耗时t的变化图及新算法PSNR对比图
图4(b)为改进的StrOMP和原始StOMP在采样率M/N不相同时Lena的PSNR值的变化情况。伴随采样率M/N的变大,两种算法的PSNR均随之降低,而且受采样率的影响较大。但是,在相同的采样率下可以明显看出,改进算法的PSNR值总是高于StOMP,平均高出0.2~0.3dB,表明改进的StrOMP重建精度增大,改进通过仿真验证是成功的。需要指出,文中在对Lena重建时,在采样比等于0.1和0.2时,加入调节因子后的阈值分别为3.328 4和3.074 5,均超出经验阈值在2≤ζ≤3这个范围,并且重建好于原阈值下的结果。
5 结束语
文中通过阐述CS理论基础知识,详细讨论了几种典型的CS重构算法,并将CS理论应用于图像中,对四种经典的贪婪算法从多角度分析重构效果,比较算法的优缺点。针对其中的StOMP算法,加入考虑稀疏度和观测矩阵行列关系的调节因子,使阈值变得更加精细,从而提出改进的分段可调节OMP算法。仿真结果表明,改进后的StrOMP算法从耗时和PSNR值上都优于StOMP算法。
[1]DonohoDL.Compressedsensing[J].IEEETransactionsonInformationTheory,2006,52(4):1289-1306.
[2]CandèsEJ,RombergJ,TaoT.Robustundertaintyprinciples:exactsignalreconstructionfromhighlyincompletefrequencyinformation[J].IEEETransactionsonInformationTheory,2006,52(2):489-509.
[3]TroppJA,GilbertAC.Signalrecoveryfromrandommeasurementsviaorthogonalmatchingpursuit[J].IEEETransactionsonInformationTheory,2007,53(12):4655-4666.
[4]NeedellD,VershyninR.SignalrecoveryfromincompleteandinaccuratemeasurementsviaROMP[J].IEEEJournalofSelectedTopicsinSignalProcessing,2010,4(2):310-316.
[5]NeedellD,TroppJA.CoSaMP:iterativesignalrecoveryfromincompleteandinaccuratesamples[J].Applied&ComputationalHarmonicAnalysis,2008,26(3):301-321.
[6]DonohoDL,TsaigY,DroriI,etal.Sparsesolutionofunderdeterminedsystemsoflinearequationsbystagewiseorthogonalmatchingpursuit[J].IEEETransactionsonInformationTheory,2012,58(2):1094-1121.
[7] 杨真真.压缩感知重构技术及其在图像融合中的应用研究[D].南京:南京邮电大学,2014.
[8]CandesEJ,WakinMB.Anintroductiontocompressivesampling[J].IEEESignalProcessingMagazine,2008,25(2):21-30.
[9] 石光明,刘丹华,高大化,等.压缩感知理论及其研究进展[J].电子学报,2009,37(5):1070-1081.
[10] 高 睿,赵瑞珍,胡绍海.基于压缩感知的变步长自适应匹配追踪重建算法[J].光学学报,2010(6):1639-1644.
[11] 甘 伟,许录平,张 华,等.一种贪婪自适应压缩感知重构[J].西安电子科技大学学报,2012,39(3):50-57.
[12]PeyréG.Bestbasiscompressedsensing[M]//Scalespaceandvariationalmethodsincomputervision.Berlin:Springer,2007:2613-2622.
[13]MunS,FowlerJE.Blockcompressedsensingofimagesusingdirectionaltransforms[C]//IEEEinternationalconferenceonimageprocessing.[s.l.]:IEEE,2009:3021-3024.
[14]TramelEW,FowlerJE.Videocompressedsensingwithmultihypothesis[C]//Proceedingsofthe2011datacompressionconference.[s.l.]:IEEEComputerSociety,2011:193-202.
[15] 李 博.压缩感知理论的重构算法研究[D].长春:吉林大学,2013.
An Image Compressed Sensing Algorithm Based on Novel Stagewise Regulation OMP Algorithm
SHI Man-man,LI Lei
(College of Science,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)
Compressed Sensing (CS) theory uses small frequency,which is mainly for sparse or compressible signal.Sampling and compressing are also implemented successfully at the same time,and can accurately recover the original signal.It focuses on the classical greedy algorithm in this paper for compressed sensing reconstruction algorithm,including four classical matching pursuit algorithms like Orthogonal Matching Pursuit (OMP),the Regularized Orthogonal Matching Pursuit (ROMP),Compressive Sampling Matching Pursuit (CoSaMP) and Stagewise Orthogonal Matching Pursuit (StOMP).Considering the reconstruction accuracy and time as evaluation standards,the advantages and disadvantages of algorithms and difference of them are given by combining with horizontal and vertical comparison.The adjustment factor for StOMP at each iteration is put considering the sparsity and the observation matrix ranks,and an improved algorithm is proposed,which makes innovations for StrOMP algorithm,named Stagewise regulation Orthogonal Matching Pursuit (StrOMP).The simulation shows the proposed algorithm can raise the accuracy of image reconstruction,and guarantee the priority of the reconstruction time of the new algorithm.
compressed sensing;greedy algorithm;image reconstruction;stagewise regulation orthogonal matching pursuit reconstruction algorithm
2016-01-18
2016-05-11
时间:2016-10-24
国家自然科学基金资助项目(61501251);南京邮电大学引进人才科研启动基金资助项目(NY214191)
石曼曼(1992-),女,硕士研究生,研究方向为信息处理理论与应用;李 雷,博士,教授,研究方向为智能信号处理和非线性科学及其在通信中的应用。
http://www.cnki.net/kcms/detail/61.1450.TP.20161024.1113.032.html
TP301.6
A
1673-629X(2016)11-0014-05
10.3969/j.issn.1673-629X.2016.11.004
