2000国家大地坐标与城市平面坐标转换方法的研究

2016-02-26魏保峰李国柱

测绘通报 2016年1期

关键词：投影面子午线点位

魏保峰，李国柱，倪　曙，马　波，张　珏

(昆明市测绘研究院，云南昆明 650051)

Conversion Method between 2000 China Geodetic Coordinate and

City Plane Coordinate

WEI Baofeng，LI Guozhu，NI Shu，MA Bo，ZHANG Jue

2000国家大地坐标与城市平面坐标转换方法的研究

魏保峰，李国柱，倪曙，马波，张珏

(昆明市测绘研究院，云南昆明 650051)

Conversion Method between 2000 China Geodetic Coordinate and

City Plane Coordinate

WEI Baofeng，LI Guozhu，NI Shu，MA Bo，ZHANG Jue

摘要：城市地方坐标系与2000国家大地坐标系(CGCS2000)之间的坐标转换一般采用七参数和四参数转换模型，各模型都有一定的适用性，受到范围限制等的制约，因此两坐标系之间的数据转换工作量成为推广CGCS2000的瓶颈。本文提出了一种城市地方坐标系与CGCS2000之间的严密转换模型。该模型的特点是均在CGCS2000椭球基准下进行相互转换；将平面转换与高程转换分开进行；建立的坐标系之间的转换是可逆的，且不损失精度。使原有城市地方坐标系下的数据成果无须转换，直接继续使用。最后通过实例分析，对提出的模型进行可行性验证，结果表明该方法能够解决转换过程中的问题。

关键词：CGCS2000；城市地方坐标系；CGCS2000城市地方坐标系；坐标严密转换

我国于20世纪50年代和80年代，分别建立了1954北京坐标系和1980西安坐标系，并在此坐标系统上测制了各种比例尺地形图，为国民经济和社会发展提供了基础的测绘保障。

在此基础上，为了满足城市建设、规划和工程施工的需要而建立了城市坐标系统，为减小投影变形，所建立的城市平面坐标系统往往相对独立，但需与国家坐标系统建立联系[1]。2008年7月1日，我国正式启用CGCS2000地心坐标系统，并在城市平面坐标系统的定义中规定：城市平面坐标系统采用的参考椭球应与CGCS2000坐标系定义的参考椭球一致[1]。而我国现有的大多城市地方坐标系与CGCS2000一般基于不同的椭球，即使采用相同的转换模型和方法，其坐标转换后成果还有一定的局限性和适用范围。在这种背景下，笔者通过大量分析与试验验证，最终确定了一套城市地方坐标与CGCS2000大地坐标的转换模型，能够在两套坐标系之间进行严密的相互转换。该模型优点是将原城市地方坐标系成果移植至CGCS2000椭球上来，可直接使用原城市地方坐标系成果数据，无须转换，可认为是在CGCS2000的基础上建立的CGCS2000城市地方坐标系。

一、理论方法

1. 坐标系的建立

坐标系是定义坐标如何实现的一套理论方法，包括定义原点、基本平面和坐标轴的指向，同时还包括基本的数学和物理模型等。在测量中的坐标系根据原点位置的不同可分为参心坐标系、地心坐标系。我国的参心坐标系有1954北京坐标系和1980西安坐标系。地心坐标系有CGCS2000国家大地坐标系。

2. 城市地方坐标系

为了满足长度变形值不大于2.5 cm/km的要求，大多数城市都建立了城市地方坐标系，建立时确立坐标系的有关元素，并根据这些元素和地面观测值求定各点在该坐标系中的坐标值。我国城市地方坐标系基本都是基于1954北京坐标系和1980西安坐标系而建立的。建立时的参数一般包括参考椭球、中央子午线、起算点坐标、坐标方位角、投影高程面、测区平均高程异常等。

3. 城市坐标系与CGCS2000转换模型的建立

城市地方坐标系和CGCS2000分别对应着各自投影面和中央子午线。其中，CGCS2000对应投影面是国家大地基准所确定的参考椭球面,对应的中央子午线是国家带的中央子午线；城市地方坐标系的投影面一般是该区域的平均高程面，其中央子午线往往穿过测区的中央。

本文的研究方法是以原城市地方坐标系的参数为参考，将城市坐标系成果移植至CGCS2000的框架上来，在CGCS2000椭球下寻找中央子午线、坐标旋转原点北东坐标、北方向加常数、东方向加常数、旋转角及尺度比等参数。根据确立后的7个参数，建立一套CGCS2000椭球下的城市地方坐标系，简称CGCS2000城市地方坐标系。

(1) 转换流程

两种坐标系之间的转换关键点为如何将城市地方坐标系下的坐标成果通过试验和分析，寻找出在CGCS2000椭球下的最佳转换参数。图1为两种坐标系之间进行相互转换的流程图。

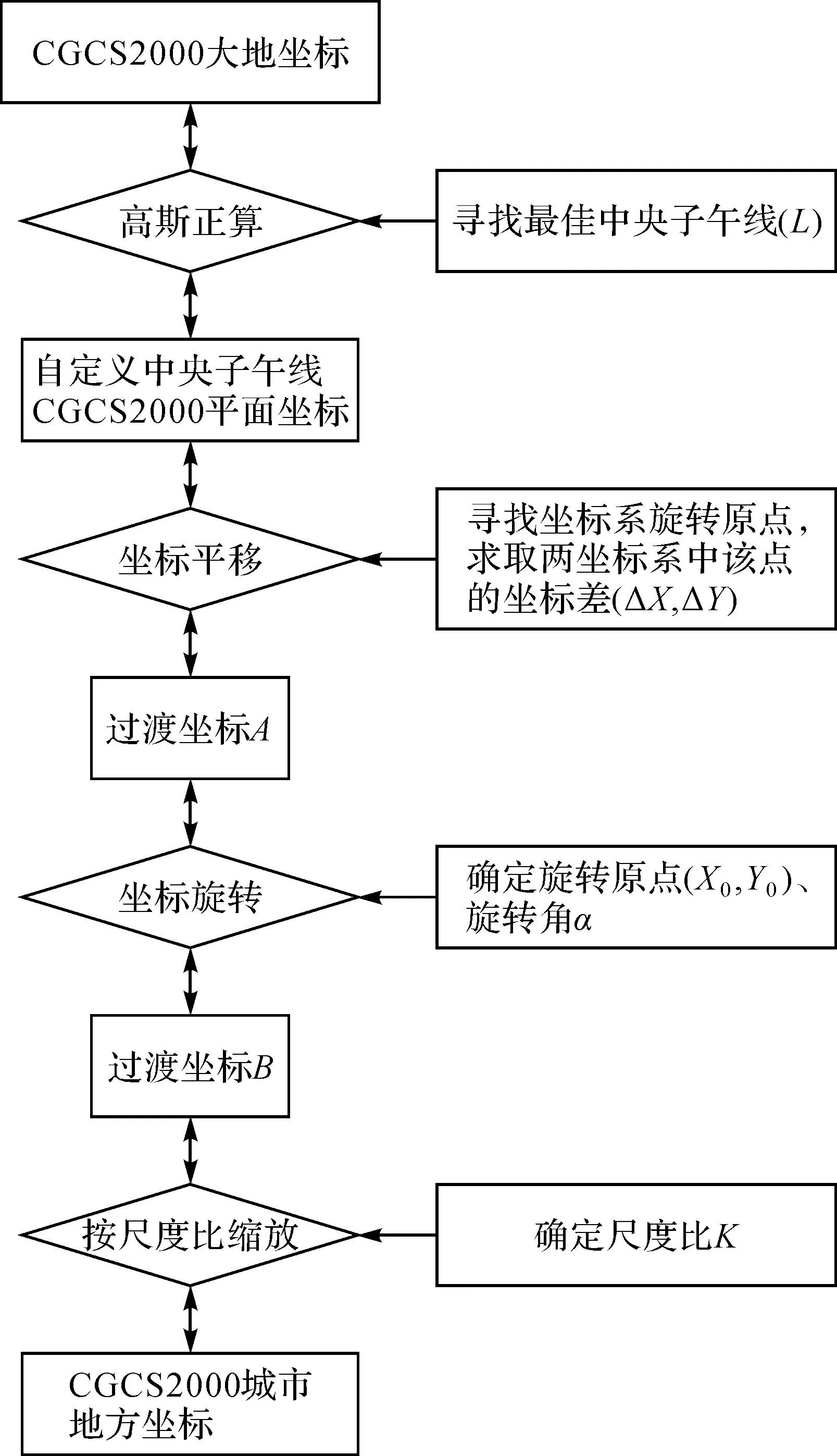
图1　转换流程

本文主要给出由CGCS2000大地坐标转换为城市地方坐标的步骤，该步骤可逆。图1为高斯正算后在平面直角坐标系下进行一系列的相似变换，与四参数有些类似，虽然看起来步骤较多，但可准确确定各参数值，为使原城市地方坐标系成果继续使用带来了可能。

(2) 转换模型

为保证城市地方坐标系与CGCS2000之间相互转换的通用性，以及未来维护和恢复的方便，该转换模型中所有的参数一旦经检验符合限差要求后，将固定下来不再进行调整，以维护后期坐标系统的稳定性。以下步骤为正算步骤，由于篇幅限制，反算步骤在这里不再一一叙述。

① 高斯正算

转换模型中CGCS2000采用的是大地坐标，其高斯正算如下

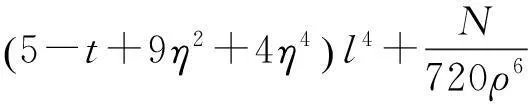
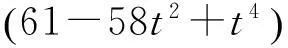
(1)

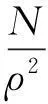
(2)

本文采用大地坐标而不采用投影坐标是考虑到城市测绘基础设施的充分利用。笔者所在单位建设CORS网中各站点均已使用了CGCS2000大地坐标，外业人员可同时获取CGCS2000大地坐标和城市地方坐标成果，方便使用。

② 坐标平移

将高斯正算后计算的坐标点进行平移，平移量为两套坐标系中旋转点的坐标差

ΔX=XCGCS2000临.旋转点-X城.旋转点

(3)

ΔY=YCGCS2000临.旋转点-Y城.旋转点

(4)

③ 坐标系旋转与尺度调整

以旋转原点为旋转点进行坐标系旋转。同时以旋转原点为圆心，所有点位均以此点为固定点，按确定的尺度比进行缩放，最终形成CGCS2000城市地方坐标系坐标。坐标旋转与尺度调整数学模型如下

(5)

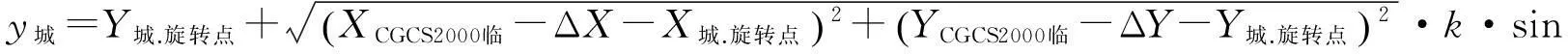
(6)

(3) 确定模型最佳参数的方法

模型中各参数均需根据各自的特点通过一定的方法进行确定。

在确定模型参数时，中央子午线的确定尤为重要，根据经验，一般在原城市坐标系中央子午线±10′之间寻找。如果不清楚原城市坐标系中央子午线，可在城市建城区中心处的子午线附近寻找，见表1、表2。

表1　CGCS2000城市地方坐标系模型参数

由表2可以看出，相同边在不同中央子午线下的长度不同，而要与原城市地方坐标系符合性最好，长度比的平方和最小的即为最佳中央子午线。

其次，旋转原点、坐标方位角可在原城市坐标系建立时的参考资料中查阅，早期的城市坐标系建立时多数采用“一点一方位”，出于保密考虑，个别城市还对坐标系进行了分、秒数级的旋转。如果无法获取这些资料，也可根据现有资料进行推测，一般旋转原点在控制网中部区域。

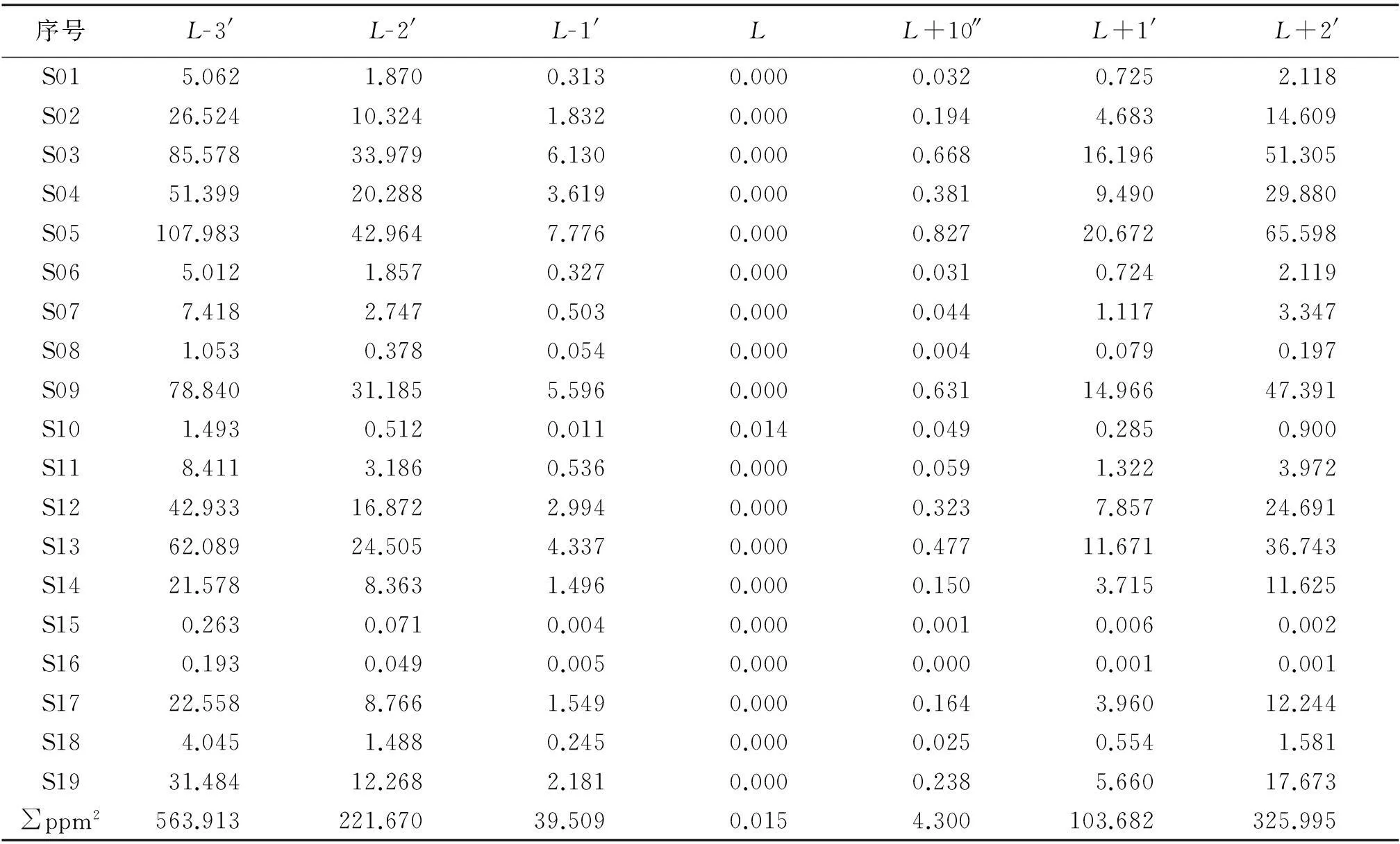
表2　最佳中央子午线确定表

其余参数(如旋转角和尺度比)可通过测区已有成果求取四参数作为参考值进行多次测试来确定，最终需要确定的参数有7个。

二、实例检验

1. 数据检验精度估计

在城市坐标系范围内，收集CGCS2000坐标系和原城市独立坐标系的成果数据，对其内符合和外符合进行检验。内符合检验主要针对模型转换成果与原控制网二维约束平差成果的坐标差比较；外符合检验主要通过一个新的项目(较高等级的项目)中与其约束后的成果进行坐标差比较。同时可检验模型转换成果与原城市独立坐标系的原有成果的坐标差比较。

精度估计是通过坐标差比较来反映。DX和DY中误差为

(7)

(8)

点位中误差为

(9)

(1) 与旧坐标比较

测区于2011年进行了整个市域地方坐标与CGCS2000坐标联测项目，本文的转换模型研究均基于该项目数据进行。在收集了测区的CGCS2000坐标和城市地方坐标成果后，使用模型转换成果与原城市独立坐标系成果进行坐标差比较，如图2、表3所示。

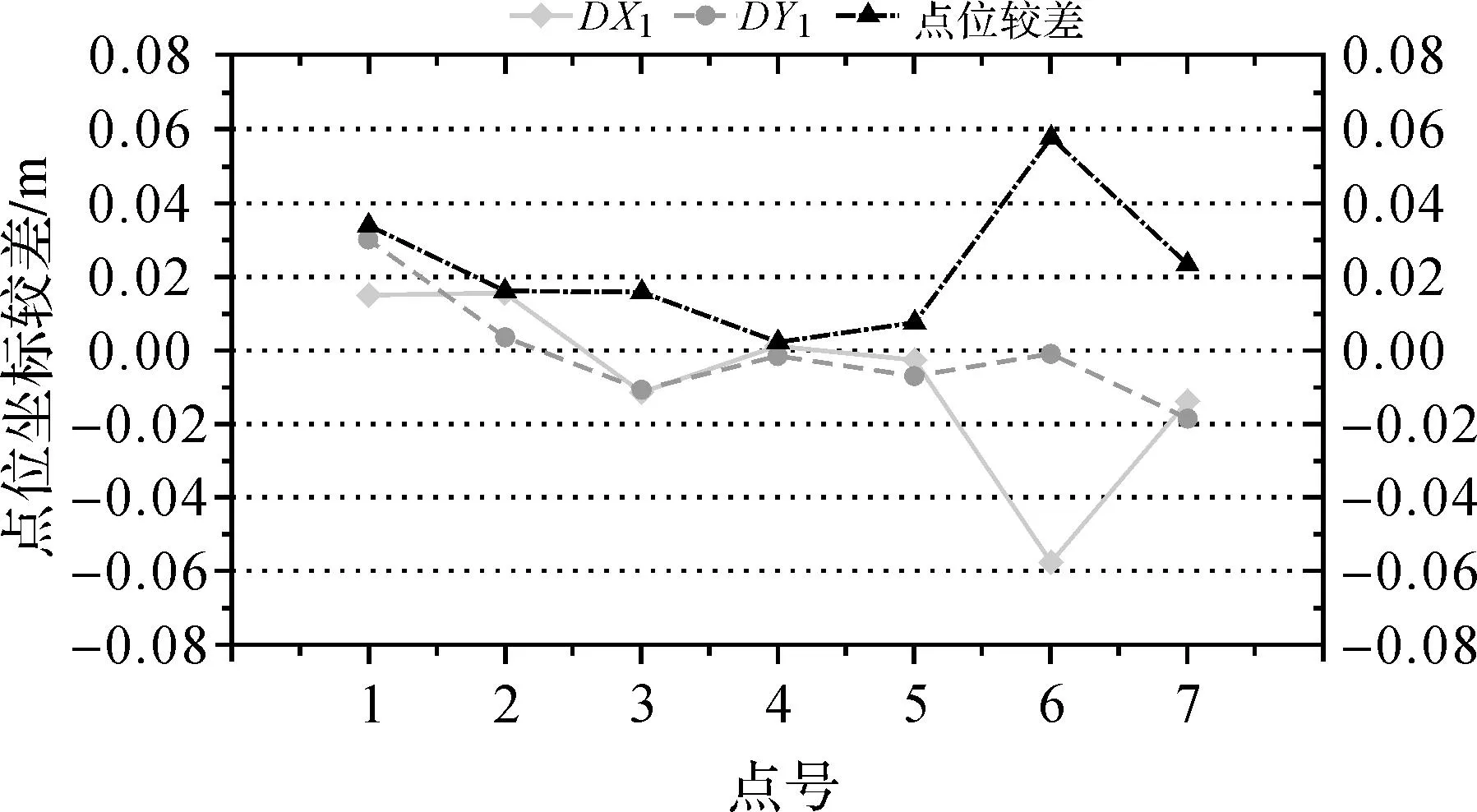
图2　转换成果与原老成果坐标比较点位较差分布

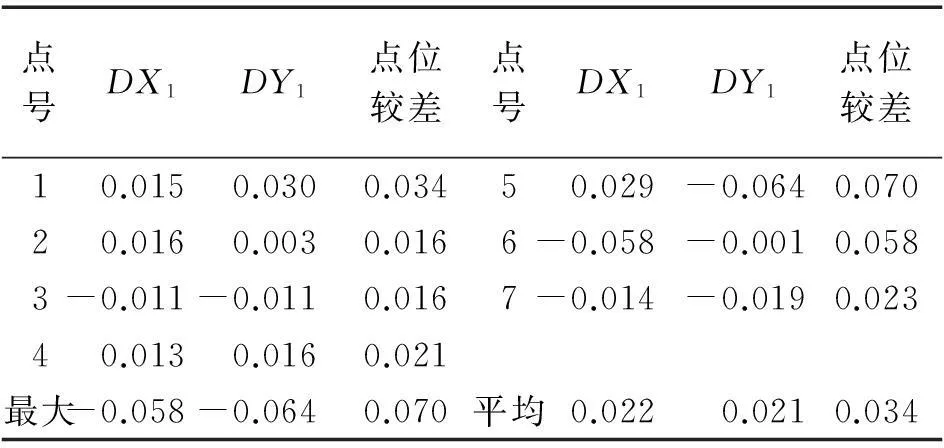
点号DX1DY1点位较差点号DX1DY1点位较差10.0150.0300.03450.029-0.0640.07020.0160.0030.0166-0.058-0.0010.0583-0.011-0.0110.0167-0.014-0.0190.02340.0130.0160.021最大-0.058-0.0640.070平均0.0220.0210.034

(2) 内符合

使用模型转换成果与项目中二维约束后的计算结果进行对比，如图3、表4所示。

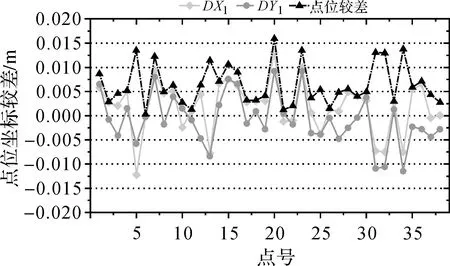
图3　转换成果与约束成果坐标比较点位较差分布

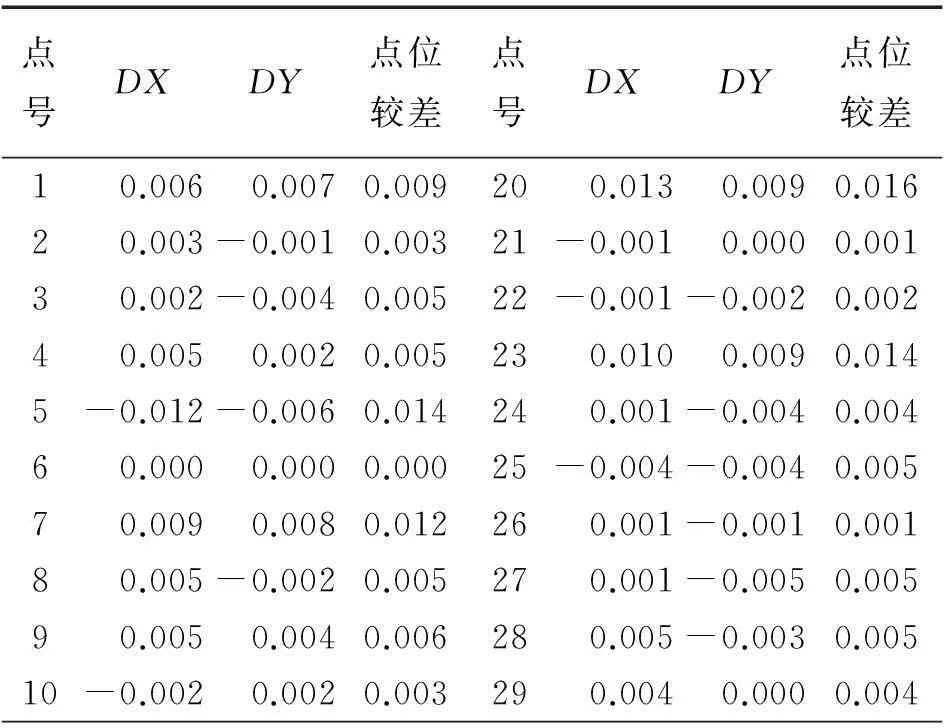
点号DXDY点位较差点号DXDY点位较差1 0.006 0.0070.00920 0.013 0.0090.01620.003-0.0010.00321-0.0010.0000.00130.002-0.0040.00522-0.001-0.0020.00240.0050.0020.005230.0100.0090.0145-0.012-0.0060.014240.001-0.0040.00460.0000.0000.00025-0.004-0.0040.00570.0090.0080.012260.001-0.0010.00180.005-0.0020.005270.001-0.0050.00590.0050.0040.006280.005-0.0030.00510-0.002 0.0020.00329 0.004 0.0000.004

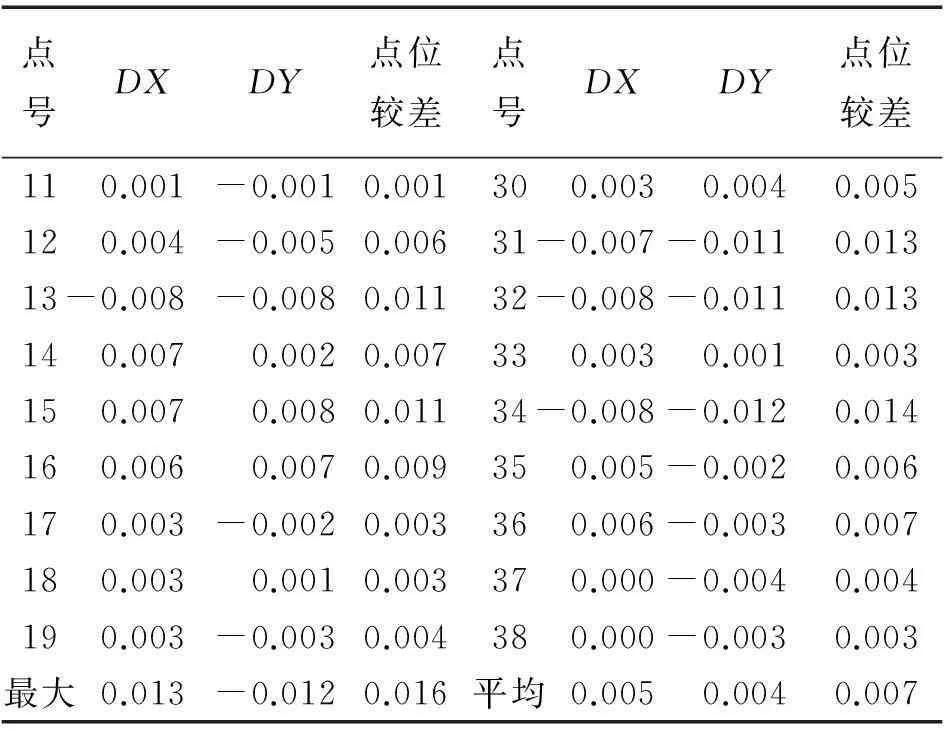
续表4

(3) 外符合

2012年笔者所在单位为该市城市轨道交通布设了基础框架网，框架网以该市的城市CORS站点作为起算数据。最终使用模型转换成果与其二维约束成果进行了比较，如图4、表5所示。

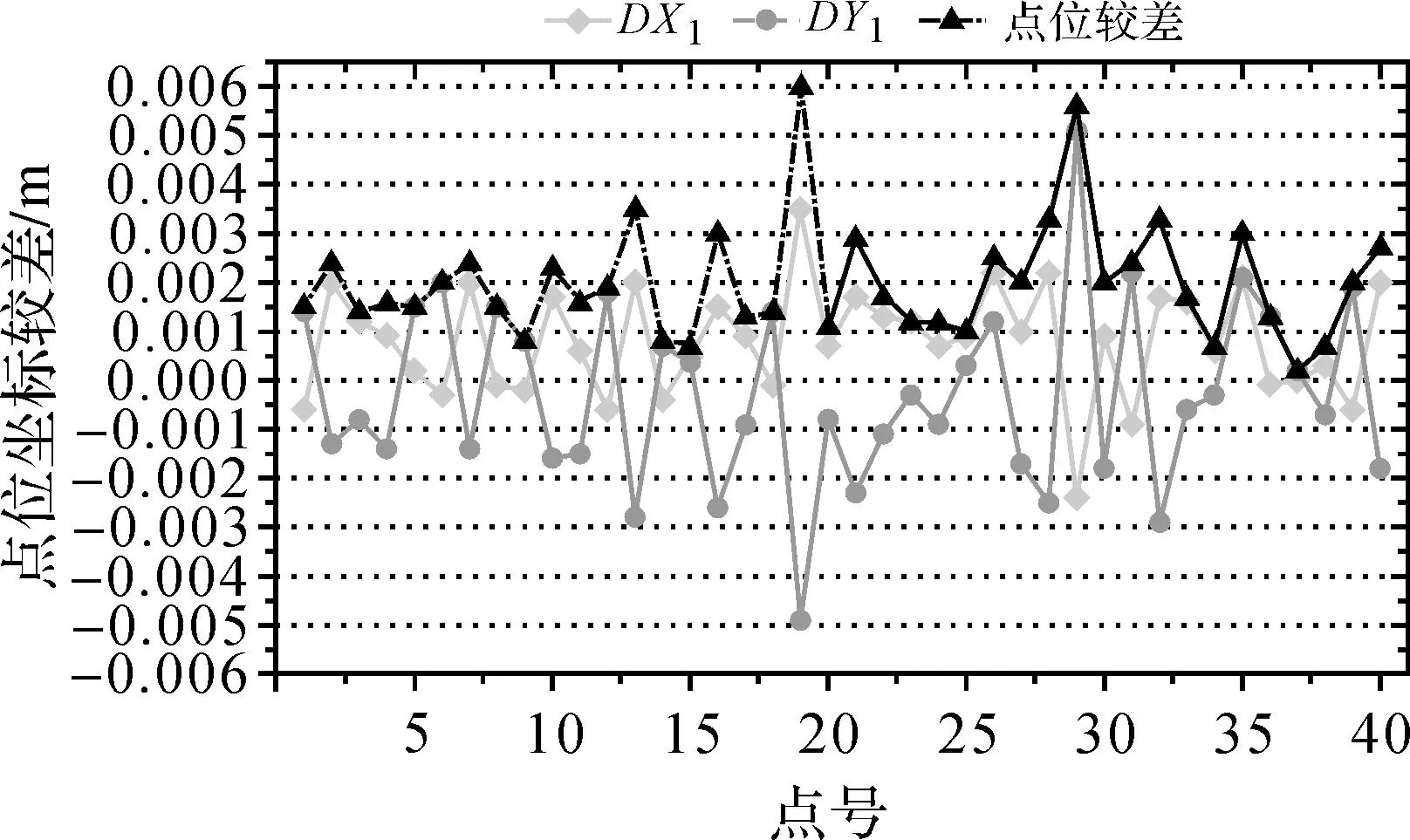
图4　城市轨道项目转换成果与约束成果点位较差分布

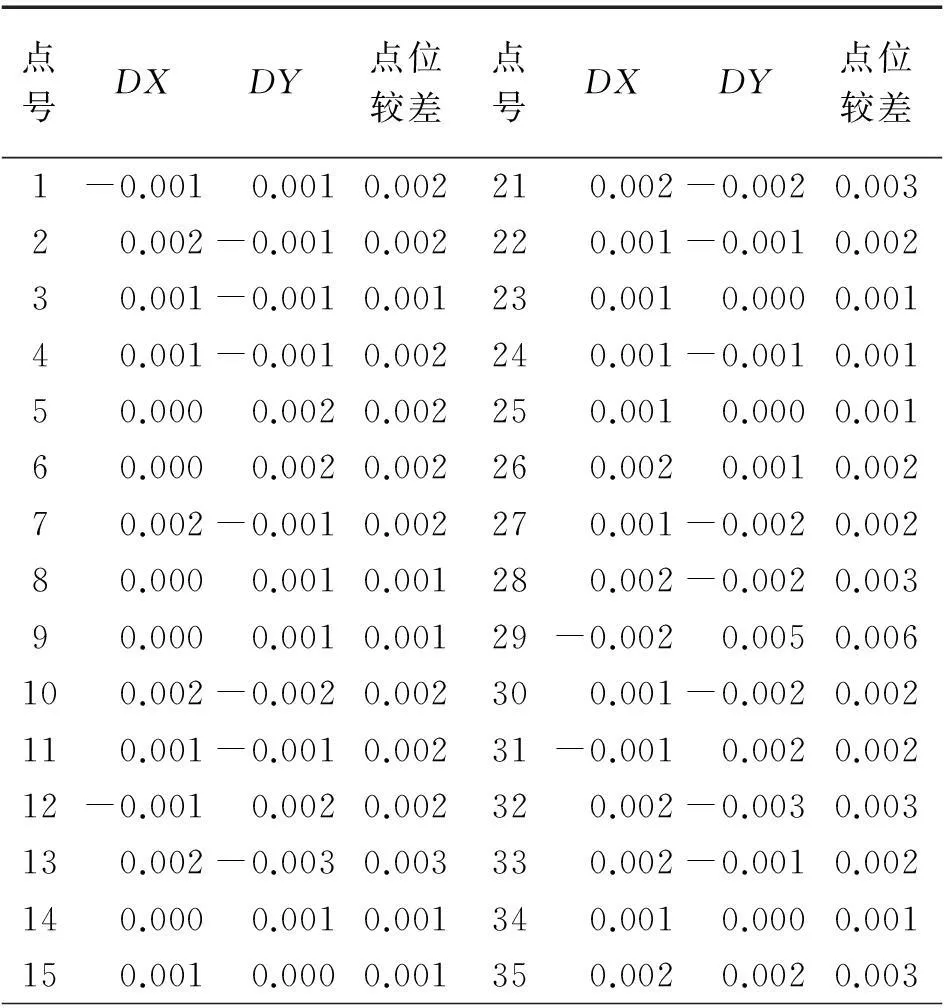
点号DXDY点位较差点号DXDY点位较差1-0.001 0.0010.00221 0.002-0.0020.00320.002-0.0010.002220.001-0.0010.00230.001-0.0010.001230.0010.0000.00140.001-0.0010.002240.001-0.0010.00150.0000.0020.002250.0010.0000.00160.0000.0020.002260.0020.0010.00270.002-0.0010.002270.001-0.0020.00280.0000.0010.001280.002-0.0020.00390.0000.0010.00129-0.0020.0050.006100.002-0.0020.002300.001-0.0020.002110.001-0.0010.00231-0.0010.0020.00212-0.0010.0020.002320.002-0.0030.003130.002-0.0030.003330.002-0.0010.002140.0000.0010.001340.0010.0000.001150.001 0.0000.00135 0.002 0.0020.003

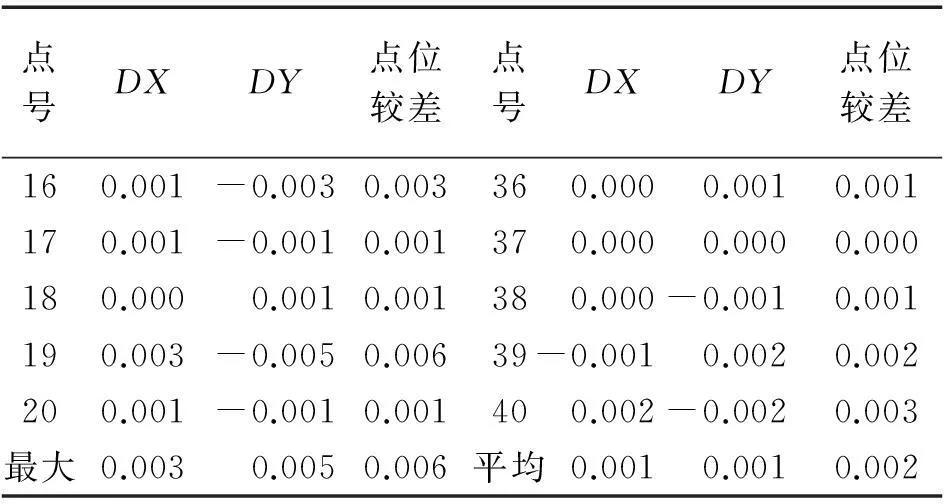
续表5

2. 结果分析

模型转换成果与原城市坐标系已知成果点位差中误差为0.034 m，最大为0.058 m；与二维约束成果坐标点位差中误差为0.007 m，最大为0.016 m。通过新项目检验后，模型转换成果与二维约束成果坐标点位差中误差为0.002 m，最大为0.006 m，见表6。

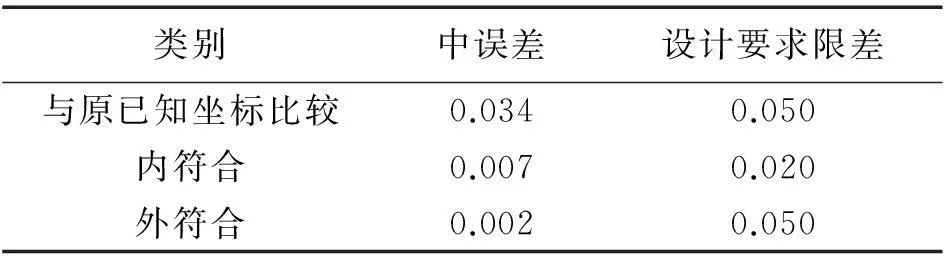
表6　点位差中误差　m

由成果对比可以看出，该转换模型在后期项目中的应用中，成果与约束成果符合性很高。因此，由转换模型可以得出，如果确定了转换模型，在后期的GNSS控制网项目中，在三维平差后可直接使用平差的CGCS2000大地坐标系成果进行转换，不需要在测区内选择一定数量的点进行约束平差，不再受已知点位分布的困扰，极大地提高了工作效率。

三、结束语

本文建立的CGCS2000坐标系与城市地方坐标系之间的转换模型转换精度良好，达到了预期设计要求的精度指标。当然，要达到转换精度的要求除模型参数的确定之外，前期的原城市地方坐标系成果精度也是决定转换结果精度的一项重要指标。

上述方法建立的转换模型只是针对一个中央子午线和一个投影面的转换，如果该城市没有多投影面但根据发展需要建立多投影面的，笔者建议通过调整尺度比的方式来实现。如果原有多个投影面的，可根据该模型建立的步骤逐步确定其他投影面的参数。

该模型的转换主要针对平面坐标，如果城市建立了区域内高精度的似大地水准面精化模型，可与该模型进行结合，实现CGCS2000坐标系的大地高与城市坐标系正常高之间的相互转换。

该转换模型的实质是通过原城市地方坐标系参数寻求一种最佳的基于CGCS2000椭球的转换参数，建立一个全新的CGCS2000城市地方坐标系。该坐标系既不改变原坐标成果，又与CGCS2000国家坐标系保持严密的转换关系，极大地减少了转换成果的工作成本，也基本上解决了CGCS2000坐标系向城市坐标系推广的一系列问题。

参考文献：

[1]中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会.城市坐标系统建设规范：GB/T28584—2012[S].北京：中国标准出版社, 2012.

[2]郭春喜, 李东.基于CGCS2000建立城市相对独立坐标系统的方法[J].测绘通报, 2012(10):5-7.

[3]中华人民共和国住房和城乡建设部.城市测量规范：CJJ/T 8—2011[S].北京：中国建筑工业出版社, 2011.

[4]贾志强.1980国家坐标系向某市地方独立坐标系的转换[J].测绘与空间地理信息, 2010, 33(1):193-196.

[5]阳海峰.2000国家大地坐标系与我国常用坐标系在大地控制成果转换方面的研究[D].西安：西安科技大学，2010.

[6]陈俊勇.中国现代大地基准——中国大地坐标系统2000(CGCS2000)及其框架[J].测绘学报, 2008, 37(3):269-271.

引文格式：魏保峰，李国柱，倪曙，等. 2000国家大地坐标与城市平面坐标转换方法的研究[J].测绘通报，2016(1)：57-61.DOI:10.13474/j.cnki.11-2246.2016.0014.

作者简介：魏保峰(1979—)，男，硕士，工程师，主要从事大地测量数据处理及精密工程测量等工作。E-mail：27707648@qq.com

基金项目：住房和城乡建设部2014年科学技术项目计划(2014-R2-032)

收稿日期：2014-11-03

中图分类号：P226