基于扩张状态观测器的异步电机定子磁链观测

罗胜华，刘登基钟庭欢

(1湖南电气职业技术学院，湖南湘潭411101；

2湘潭大学信息工程学院，湖南湘潭411105；

3湖南工程学院湖南省“2011协同创新中心”，湖南湘潭411101 )



基于扩张状态观测器的异步电机定子磁链观测

罗胜华1,3，刘登基2,3钟庭欢2,3

(1湖南电气职业技术学院，湖南湘潭411101；

2湘潭大学信息工程学院，湖南湘潭411105；

3湖南工程学院湖南省“2011协同创新中心”，湖南湘潭411101 )

摘要通过采用扩张状态观测器(ESO)，提出了一种不依赖定子电阻的定子磁链观测方法。在定子磁链定向的同步旋转坐标系下，将定子电流状态方程所有含定子电阻项合并成不确定项；并将不确定项扩张成一阶新状态变量。用扩张状态观测器观测出不确定项的值，进而准确的观测出定子磁链。针对提出的方法，在Matlab/Simulink中搭建模型进行仿真并在物理平台进行了实验验证，结果表明此方法有效。

关键词定子电阻；定子磁链；扩张状态观测器；直接转矩

0引言

异步电机由于效率高、结构简单被工业生产广泛使用，随着电力电子技术与现代控制理论的发展，尤其是直接转矩控制技术(DTC)的出现，使异步电机调速性能得到进一步的提升。直接转矩控制技术思想新颖，方法简单，对电机参数依赖少，简化了复杂的计算，且具备优良的动、静态性能。

常用定子磁链计算方法有电流模型(i-n)与电压模型(u-i)以及混合模型法。与电压模型相比，电流模型依赖电机的参数多，受电机参数影响大。混合模型结合了流模型和电压模型，分别在高速和低速的情况下切换到电压模型和电流模型，但是一直以来混合模型的平滑切换问题没有很好地解决，所以很少被采用。相比之下，电压模型只与定子电阻有关，结构简单，因而被广泛采用。异步电机实际运行时，其定子电阻阻值受温度影响，阻值变化最高可达额定值的50%[1]。高速运行时，定子电阻分压很小，其阻值变化可以忽略不计。而低速运行时，定子电阻分压较大，其阻值波动对定子磁链观测的准确性有较大影响，进而导致转速发生波动及电磁转矩脉动变大[1]，因此低速运行时，电压模型法计算定子磁链将产生较大的误差，所以定子磁链的准确辨识是十分有意义的工作。

为解决低速下定子磁链的辨识问题，许多学者做了大量的研究，文献[3]采用神经网络对定子电阻进行估算，获得比较好的结果，但神经网络由于计算量大，目前在硬件上难以实现；文献[4]在矢量控制的基础上采用了复合控制，反步控制器用于控制电流，扩张状态观测器控制速度，仿真效果较好。但文献忽略了过多的扰动，仅达到了控制的快速性和稳定性，但未考虑系统的鲁棒性，实际作用有限；文献[5]将电机运行时内部扰动和外部扰动用ESO观测出来并加以补偿。文中采用在线的方法对扰动进行观测，然后进行解耦控制，仿真效果较好，但由于在线观测功能有限；且解耦过程复杂实际应用中价值有限。文献[6-7]采用可以切换的参考模型自适应法来同时辨识磁链和定子电阻，仿真效果较好，但系统比较复杂，在工业实践中是难以实现；文献[8]通过构造ESO观测器辨识包含速度与磁链信息的不确定项，通过ESO观测器获得磁链与速度的观测值，理论上可以行，但未考虑定子电阻变化对定子磁链观测的影响，从而在应用过程中会出现误差。

本文先对异步电机的数学模型进行分析，通过坐标变换得到旋转坐标系(d-q)下的电流状态方程，将所有含定子电阻不确定项合并扩张成一阶新的状态，采用扩张状态观测器观测出这个不确定项，由于这个不确定项包含了定子磁链的信息，从而可以直接由它得到定子磁链的准确值。

1ESO的原理

为解决不确定对象难以状态观测的问题，韩京清教授首先提出了一种新的方法-扩张状态观测器(Extended State Observer)。ESO是一种非线性鲁棒控制技术，它比相同条件下的观测器多了1维状态，正是由于扩张出来的这1维状态，它不仅可以使控制对象的状态重现，而且可以同时估计出控制对象模型的不确定项与外部扰动，从而提高了系统的稳定性。文献[9]提出了ESO的概念和方法。现简要介绍ESO。

设有一阶非线性系统如下

(1)

式中，x—系统的状态变量，可以由输出测得；f(x,t)—系统的不确定部分；g(t)—模型的外部扰动；u(t)—系统的输入；将系统的不确定部分与外部扰动作为一个整体，扩张成一个新的状态f，则原系统变为

(2)

式中，f—系统的总扰动。对式(2)构造扩张状态观测器如下

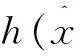
2扩张状态观测器的分析与设计

2.1异步电机扩张状态观测器的设计

首先通过3s/2r的坐标变换，可得定子磁链旋转坐标系(d-q)下的异步电机动态数学模型

Te=np(isqψsd-isdψsq)

(4)

式中，ψsd,ψsq—磁链在d,q轴上的磁链分量；isd，isq—d,q轴上的定子电流分量；usd,usq—d,q轴上的定子电压分量；Rs,Rr—定子电阻与转子电阻;Ls,Lr—定子电感、转子电感；ω1—定子同步角频率；ω—转子角频率。

式中，σ=1-Lm2/LrLs,Tr=Lr/Rr

对式(4)进如下变换

Te=np(isqψsd-isdψsq)

(5)

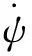
(6)

我们对式(6)进行离散化，采样周期为T则

(7)

定子电流的角频率可由下式实时计算得出

(8)

式中，ω1(k)实时的定子的同步角速度ω1。对于式(8)用离散的数字积分器进行积分就可以计算出定子磁链的方向角。这里由于采用了定子磁链定向，d轴与定子磁链矢量重合，所以定子磁链的方向角也就是d坐标轴和α坐标轴之间的夹角，这样就得到了2s-2r坐标变换时所需要的夹角。同时记ωs=ω1-ω，而转子角频率ω可以实时测量出来，即ωs是一个常量。因此，异步电机按定子磁链定向的动态模型为式(5)可变为式(9)

ψsd=∫(usd-Rsisd)dt

Te=npisqψsd

(9)

分析式(9)第一行可以看到，定子磁链电压模型(u-i)计算磁链时需要定子电阻和积分器的参与，才能观测出定子磁链。一直以来电压模型定子磁链计算法有如下的缺点

(1)在低速时会出现初始值的误差导致的积分偏移，使系统运行不稳定。

(2)低速时电机定子端电压很小,Rs引起的压降严重影响定子磁链运算的精度，导致电机低速运行时不稳定,随着温度的上升Rs也会发生变化，进一步的影响磁链观测的准确性。

为准确观测出定子磁链，本文提出了一种新型扩张状态观测器，克服了定子电阻变化以及积分器对定子磁链计算带来的不利影响。下面主要是从式(9)中计算出精确的定子磁链幅值。分析式(9)选取q轴电流分量，先将式(9)q轴电流状态方程中所有包含磁链的项视为不确定部分，并将其提取出来扩张成一个新的状态。

f1=a(t)

(10)

式中，a(t)—有界的未知函数；f1—系统的不确定项；ωsisd—系统实时可测量

(11)

对式(10)构造扩张状态观测器

(12)

2.2观测器参数的确定

扩张状态观测器的精度与β1,β2密切相关，这几个参数的选取主要有以下方法：单纯形法、动态参数配置法；文献[11]对比了反馈函数取线性和非线性时观测器的性能，指出非线性反馈函数要优于线性反馈函数；文献[12]引入带宽的概念用二项式(s+w)m的展开式系数来确定参数。本文采用文献[12]中状态观测器参数整定方法确定这几个参数。

首先本文ESO中取如下的非线性函数

(13)

式中，参数的选取可以借鉴已有的工程经验，从文献[12]得知：0<α<1,δ取(2～3)h，h为仿真步长

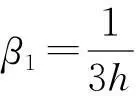
(14)

以上的工程经验只是提供了参数的数量级，有了这个大致的范围，可以通过调试选择出合适的β1、β2值，具体的参数选择过程可以参考文献[13]。本文通过大量的实验对比得出了一组比较理想的参数

β1=45，β2=337。

3定子磁链幅值的计算

由于式(11)包含了定子磁链的幅值信息，把式(11)改写成下面的形式

(15)

从式(9)中：Te=npisqψsd，结合式(15)就得到转矩值。由于整个观测方案中定子电阻没有参与计算，该扩张状态观测器对定子电阻变化有较强的鲁棒性，克服了传统定子磁链计算电压模型法的缺陷。

4仿真与实验

4.1仿真分析

为验证本方法的有效性，在Matlab/Simulink8.0中搭建仿真模型进行仿真实验，根据文献[14]重新搭建了仿真用异步电机模型，电机的参数为

Rr=0.27W,Ls=2.63mH,Lr=3.73mH,Lm=6.46mH,f=50Hz,J=0.089k g·m2，np=2极对数。为证明本文提出的磁链观测的方法的有效性，在电机运行时对定子电阻施加的扰动信号如图1所示[15]。

采用常规的带积分器的定子磁链观测方法与本文所提的方法对定子磁链分别进行观测，仿真得到定子电流观测波形与定子磁链观测波形分别如图1、图2、图3、图4、图5、图6所示。

通过图2仿真结果可知，当定子电阻发生变化时，观测器观测出的电流仍然能准确跟随实际的电流。

通过对比图3、图4定子磁链仿真结果可知，当定子电阻发生改变时，常规电压型磁链观测算法得到的结果受电阻的影响较大，可以看到定子磁链幅值波动比较大，波形不光滑；而本文提出的ESO定子磁链观测法能抑制定子电阻变化对磁链观测造成的不利影响，从图3中可以看出定子磁链波形波动比较小，曲线也远比图4曲线光滑。由于定子磁链观测精度提高了所以相应的转矩波动也会减小。

通过图5、图6的对比，我们可以发现ESO磁链观测法所得到的转矩波动远小于常规定子磁链观测法得到的转矩。因此本文提出的ESO磁链观测法是比较有意义的。

4.2实验分析

为验证上述观测器的可靠性，搭建了基于TI公司生产的数字信号处理器DSP28335的实验平台，系统的硬件构成如图7所示，主电路包括主调压器，15kW的变频调速整流器，三相六桥臂IGBT和功率驱动模块，一台功率15kW的Y型三相异步电机，电机主要参数与仿真模型参数一致。为获取电流和磁链波形通过 DSP串行通信口，把实验过程中的数据发送到上位机并保存，然后用Matlab读取数据并画出硬件结构图。

采用3ms的控制周期，开关频率为2.5kHz,采样频率为5kHz,定子电阻变化对定子磁链的影响主要表现在低速阶段，因此电机转速设为60r/min，分别采用带积分器的电压模型与本文设计的ESO观测器对定子磁链进行观测。实验过程中将数据通过串口发送至上位机，用Matlab作图得到如图8、图9、图10所示。

图8为电流实际值与观测值，通过对比有，ESO观测器能够比较准确的观测出电流的实际值。对比图9、图10发现，ESO磁链观测器能较好的观测出定子磁链轨迹，而采用电压模型计算出的定子磁链受定子电阻的波动影响较大，产生了较大的波动。

5结语

本文通过异步电机同步旋转坐标系下动态数学模型的分析，通过扩张状态观测器，在定子电阻不确定情况下，对定子磁链进行准确观测。实验表明，本文设计的观测器能在定子电阻波动下准确辨识出定子磁链，而常规磁链计算方法得到的磁链幅值有较大波动。仿真结果还表明由于定子磁链观测精度的提高，转矩的波动也相应减小。综上所述，该扩张状态观测器辨识方法对定子电阻的变化有较强的鲁棒性，具有一定的应用价值，进一步完善后可以应用于工业生产。

参考文献

[1]王红梅, 阮毅, 徐静. 定子电阻变化对异步电机按定子磁场定向控制系统性能的扰动分析[J].电气传动自动化,2004, 26(1):14-17.

[2]Cristiano Maria Verrelli, Alberto Savoia, Michele Mengoni. On-Line Identification of Winding Resistances and Load Torque in Induction Machines [J]. IEEE Transactions on Control Systems Technology .2014,22(4),1629-1637.

[3]Mahoud,I.M.Stator Resistance Identi cation using Arti cial Intelligent technique for the Adaptive Controller of Magnetically Saturated Induction Motor [C]// International Conference on Inteligent Systems Design and Application. Cairo :Intelligent Systems Design and Applications(ISDA),2010: 1365-1370.

[4]薛树功,瞿成明,魏利胜.永磁同步电机自抗扰反步控制[J].计算机工程与应用,2012,03:209-211.

[5]Li Hui, Xing Qiao Liu, and Jing Li. “Three-Motor Synchronization Control Strategy Based on the New Speed Sensorless Active Disturbance Rejection Control.” Applied Mechanics and Materials. Vol. 602. 2014.

[6]Zhen Li, and Longya Xu. “Sensorless field orientation control of induction machines based on a mutual MRAS scheme.” Industrial Electronics, IEEE Transactions on45, no.5 (1998): 824-831.

[7]佘致廷,郑勇,袁俊波. 带定子电阻辨识的异步电机无速度传感器直接转矩控制[J].电气传动，2011,41(5),10-14.

[8]林飞，张春朋，宋文超.基于扩张状态观测器的感应电机转子磁链观测[J].中国电机工程学报，2003,23(4),145-147.

[9]韩京清.一类不确定对象的扩张状态观测器[J].控制与决策，1995,10(1),85-88.

[10]巫庆辉, 邵诚. 跟踪-微分器在感应电动机定子磁链估计中的应用[J].机械工程学报，44.12 (2009): 291-295.

[11]王海强, 黄海. 扩张状态观测器的性能与应[J].控制与决策,28.7 (2013): 1078-1082.

[12]Dapeng, Ye, Paul P. Lin, and Gao Zhiqiang. “Research on fault diagnosis using extended state observer.”Chinese Journal of Scientific Instrument 29, no.4 (2008): 696.

[13]韩京清. 扩张状态观测器参数与菲波纳奇数列[J].控制工程，2008,15(增刊),1-3.

[14]陈伯时.电力拖动自动控制系统.第一版[M].北京：机械工业出版社，2003,205.

[15]吕伟杰，刘鲁源.小波网络在直接转矩控制定子电阻辨识中的应用[J].中国电机工程学报,2004,24(4)，116-119.

Stator Flux Linkage Observation of Induction Motor Based on the

Extended State Observer

LuoShenghua,LiuDengji,andZhongTinghuan

(1.Hunan Electrical College of Technology, Xiangtan 411101, China；2.College of Information Engineering, Xiangtan University, Xiangtan 411105, China；3.Hunan Institute of Engineering “2011 Collaborative Innovation Center”, Xiangtan 411101, China)

AbstractThis paper proposes a stator flux linkage observation method based on the extended state observer (ESO), which is independent of stator resistance. Under synchronous rotating coordinate system of the oriented stator flux, all stator resistance items contained in stator current state equation are combined into uncertain items; and uncertain items are expanded into a new first-order state variable. ESO is used to observe the values of uncertain items, and then stator flux linkage is accurately observed. For the proposed method, a model is set up in matlab/simulink to carry out simulation and experimental verification in physical platform, and the result demonstrates that this method is effective.

Key wordsStator resistance；stator flux linkage；extended state observer；direct torque

收稿日期：2015-11-09

作者简介：罗胜华男1979年生；硕士研究生，讲师，主要研究领域：智能控制理论与应用，电机与电气控制.

中图分类号：TM301.2

文献标识码：A

文章编号：1008-7281(2016)01-0026-006

DOI:10.3969/J.ISSN.1008-7281.2016.01.08