基于虚单元法求解渗流自由面的曲线拟合法

孙伟建，侯兴民，李远东，郑珊珊

(烟台大学土木工程学院，山东烟台264005)

基于虚单元法求解渗流自由面的曲线拟合法

孙伟建，侯兴民，李远东，郑珊珊

(烟台大学土木工程学院，山东烟台264005)

渗流在坝坡稳定及坝坡变形中起关键作用，渗流自由面的确定是渗流计算的主要内容之一。目前，求解渗流自由面经常采用虚单元法，但是该法需不断调整通过自由面的单元，迭代效率慢且易造成单元畸形。对有限元法求解的自由面节点水头做曲线拟合，无需调整单元，即可得到高精度的渗流自由面曲线。应用所提方法求解工程实例，计算结果表明该方法精度高、稳定性好、计算效率高，计算结果与实际自由面形状更吻合。

渗流自由面；固定网格法；有限元；虚单元法

0 引 言

从20世纪开始，渗流对工程的影响已受到广泛重视。无压自由面的渗流研究是水利工程、岩土工程等问题的一个重要研究课题。只有确定出自由面的位置，才能确定渗流区的范围，才能正确的认识水在坝坡稳定及变形分析中的作用，以减轻水的渗流对结构的危害。由于自由面(二维渗流分析时为浸润线，三维渗流分析时为浸润面)和溢出面的位置属于非线性边界问题，如何高效简洁的处理并确定出渗流自由面的位置，以及保证迭代过程收敛的稳定性是该问题的关键。

目前，自由面问题的求解方法主要是有限元法，有限元法分为移动网格法和固定网格法两大类。移动网格法[1]是确定渗流自由面的传统有限元法，该方法先根据经验假定一个自由面，并将其作为可移动边界，在迭代过程中不断调整网格形状，修改自由面的位置，直到自由面位置稳定为止。移动网格法虽迭代收敛性好，但存在缺陷，例如事先确定的自由面位置必须和实际自由面位置较为接近，每次需重新形成渗透矩阵，计算量大，同时，在不断调整网格时易造成单元网格的畸形或重叠，影响计算精度。

为了克服变网格法的局限，学者们开始尝试采用扩大分析系统的办法，自Neumann于1973年提出用不变网格分析有自由面渗流的Galerkin法以来，先后出现了多种固定网格法，将渗流区域与非渗流区域结合起来形成总分析系统，并引入边界条件作分析，以达到求解过程中无需变更单元网格的目的。方法大致分为两类：一类是调整流量法，如王媛、潘树来等[2-3]的改进初流量法等；另一类是调整单元渗透矩阵法，如Bathe的单元渗透矩阵调整法、朱军的改进单元渗透矩阵调整法[4]、王贤能等的高斯点法[5]、陈昌禄的变单元渗透系数法[6]。此外，为了解决或部分解决单元、网格对数值分析的严重限制，应用无单元法来求解渗流自由面[7-11]。葛锦宏等将无单元法引入到有自由面的渗流计算中，提出了有自由面渗流分析的无单元法；沈振中在采用罚函数处理渗流边界条件的同时，给出了罚因子的具体表达式，将无单元法用于求解堤坝渗流问题；M.Darbani提出了自由面浅水方程的无网格法；Yu-xin Jie提出了基于Voronoi形状函数的自然单元法；Tang Jing采用罚函数无单元法求解复杂土石坝渗流场。以上工作均在自由面求解的精度以及效率方面取得较大的改进。另外，许多学者在此基础上加以创新，采用不变网格基础上的变网格法，以提高计算的精度和效率，如吴梦喜等提出的虚单元法[12]，黄蔚的丢单元法[13]，苏枋的丢弃单元法在三维渗流分析中的应用[14]。

本文在虚单元法的基础上，提出了一种渗流自由面的曲线拟合法，选取适应能力强的三角形单元进行有限元分析，无需重新调整跨自由面单元，即可得到精度很高的曲线自由面。

1 渗流的基本理论和边界条件

根据达西定律和地下水运动的连续性条件，不考虑土体和水体的压缩性，均质各向异性土体的稳定渗流满足偏微分方程

(1)

式中，h是水头函数；kx、kz分别为以坐标x、z为渗透主方向的渗透系数。

渗流基本微分方程的边界条件有两类。第一类边界条件又称水头边界条件，为边界上给定位势函数或水头分布。在稳定渗流场中，淹没水中的渗流边界为等势面或等水头面，即常数，该常数通常为上、下游水位。设Γ1为具有给定水头的边界，则边界条件可写为

(2)

第二类边界条件又称流量边界条件，为在边界上给出位势函数或水头的法向导数，表示为

(3)

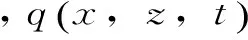
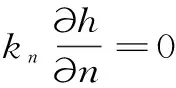
2 曲线拟合法原理

虚单元法以上一次有限元计算求得的节点势为基础，用插值法与逼近法求出自由面与单元边线的交点，将自由面穿越的母单元作为变形单元，自由面将单元分成上下两个区域，自由面以上的区域在下一次计算时不参与形成渗透矩阵，自由面以下为渗流计算区域，该域逐步逼近渗流实际区域，所得流场逐步逼近真实解。

(1)对土石坝进行全域规则划分。首先对坝体进行竖向和横向剖分，得到规则的四边形单元，再对各四边形单元进行同方向对角线连接，剖分为三角形单元，节点编号按照由左向右的顺序，由上而下依次编号。

(2)释放第一类边界条件，得到所有节点的水头值，即求解矩阵线性代数方程

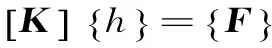
(4)

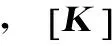
(3)由自由面满足的边界条件h=z，即在跨自由面单元中其边界条件h=z与h=N1h1+N2h2+N3h3联立求得自由面的位置，其中Ni为形函数。

(4)根据最小二乘法，由全域划分求解出的自由面的水头值拟合一条高次递减曲线，使曲线满足目标函数

(5)

式中，ωi为自由面节点的权重；φ*(xi)为待求近似函数；m为过自由面节点数目；φ为函数类型。由于最小二乘法不能保证近似函数通过已知点，可通过选取适当的权函数将此误差控制在一定的范围。本文所用的方法为三次曲线拟合，自由面节点的权重取1，所拟合的高次曲线即为精确的自由面。

进行曲线拟合时，纵向水头差值不宜过大，以确保拟合曲线为顺次递减曲线，要求在划分网格时，单元适当的划分多一些，即可确保水头求解的精确性，又可确保拟合的曲线更加符合自由面形状。为确保拟合曲线的准确性，本文采用基于全域总势能确定溢出点，此方法可以较为准确地确定溢出点。

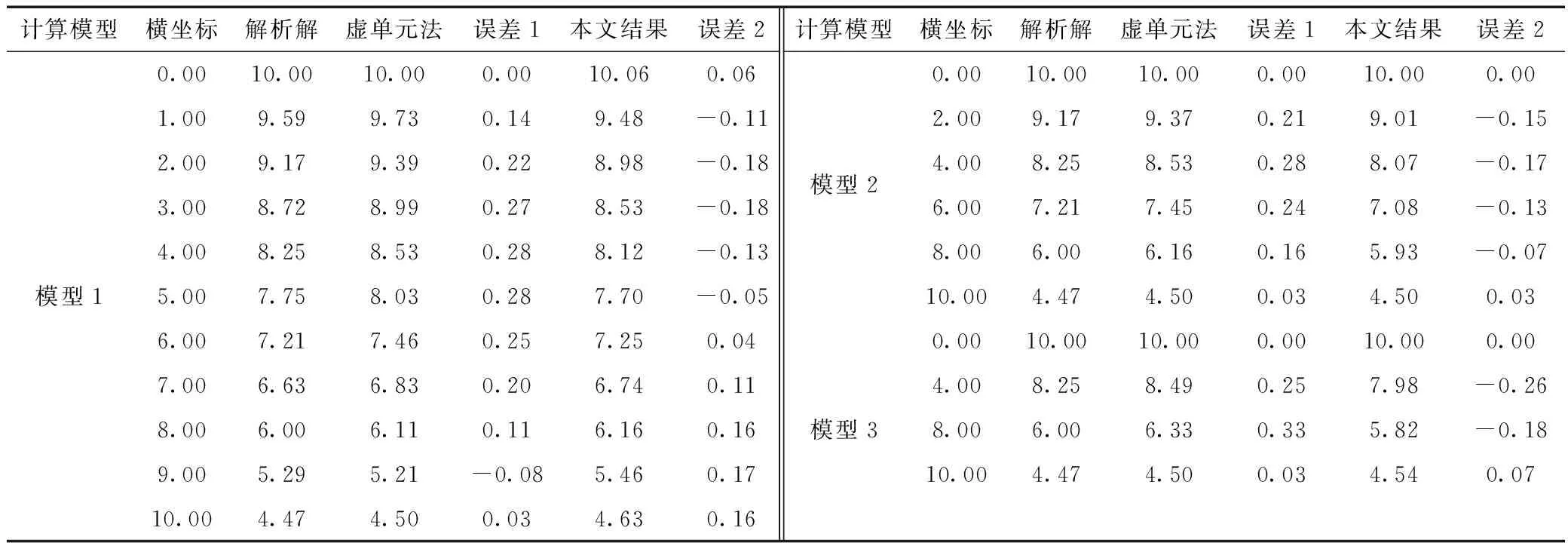
表1 解析解与数值解自由面位置数据对比 m

图1 均质矩形坝网格剖分示意

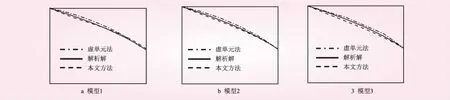
图2 自由面线形示意

3 算例

3.1 有解析解矩形均质土坝

以10 m×10 m均质土坝作分析，土坝上下游水位分别为10 m和2 m，底部为不透水边界，下游渗出面边界取为h=z。该问题自由面的解析表达式为y2=100-8x。建立3个单元尺寸不同的计算模型(见图1)用于有限元计算：①模型1。网格划分为200个直角边均为1m的三节点直角三角形平面单元；②模型2。网格划分为50个直角边均为2m的三节点直角三角形平面单元；③模型3。网格划分为18个三结点直角三角形平面单元。利用自编的二维有限元程序计算3个模型，自由面线形分别见图2，用本文方法求得的自由面位置与虚单元法精度到0.01m求得的自由面位置、解析解结果对比，结果见表1。

由表1中的数据可以看出，虚单元法(精度为0.01m)随着网格的加密，计算精度也越来越高。在进行有限元计算时网格划分的越密，计算所需的时间会越长。本文方法不需重新划分网格，仅需一次全域求解，通过最小二乘法进行高次曲线拟合即可得到精确解。本文方法与解析解最大误差分别为0.18、0.17、0.26m，精度比虚单元法高。由图2可看出本文方法拟合的高次曲线与解析解曲线更加接近，图形更加吻合。

3.2 有解析解的均质梯形坝

梯形坝渗流在工程中比较常见，如用于挡水的土石坝和基坑开挖的围堰堰体等。现以不透水地基上均质土石坝为例，坝高17m、长97m，上、下游水位分别为15、4m。本算例中网格划分为240和714个三角形单元，大网格划分单元及求解曲线分别见图3、图4。利用本文编制的有限元程序求解坝体自由面的位置与虚单元法求解的自由面位置进行比较见表2。

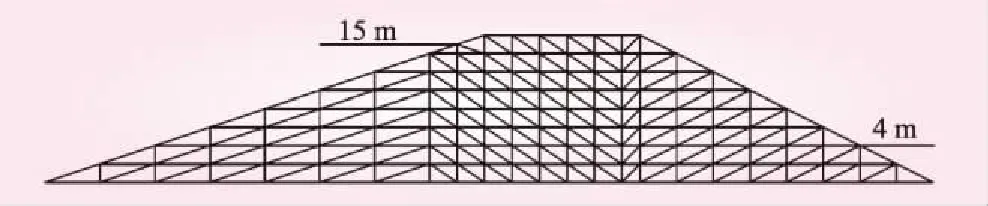
图3 均质梯形坝大网格剖分

图4 均质梯形坝大网格剖分下三种自由面的比较

由表2及图4可以看出，本文方法在求解自由面时与虚单元法求解自由面位置相差不大，虚单元法为精确到0.01m时的自由面位置。虚单元法在求解自由面是需不断重新调整跨自由面单元，容易造成网格畸形，严重影响计算精度，且需不断调整自由面节点位置，计算效率较低。本文方法仅需划分一次网格，不需对跨自由面单元进行处理，对全域求解后，用最小二乘法对跨自由面单元中高程等于水头的点进行高次曲线拟合，形成一条近似真实自由面曲线。由此算例可看出，本文方法在求解自由面时无需重新划分网格，求解效率高，稳定性好，精度高。

4 结 论

渗流在坝坡稳定及坝坡变形中起关键性作用，渗流自由面的确定是渗流计算的关键内容之一。本文提出了一种曲线拟合法，并编制有限元程序，应用于计算模型及工程实例中得到如下结论：

表2 两种数值方法计算不同网格划分自由面位置数据对比 m

(1)本文在全域求解的基础上，应用最小二乘法理论对全域求解后的自由面节点进行逐次递减的高次曲线拟合，无需多次迭代，简化了求解过程。

(2)本文方法与虚单元法相比，无需重新划分网格，只需进行一次网格划分即可求解出精确的自由面曲线，避免了全域求解后重新调整跨浸润面单元造成的网格畸形。

(3)通过实际工程算例表明，即使采用大网格划分，本文方法也可较高精度地求解出自由面曲线。

[1]ZIENKIEWIEZ O C， TAYLOR R L. The finite element method[M]. New York： Mcgraw-Hill， 1991．

[2]王媛. 求解有自由面渗流问题的初流量法的改进[J]. 水利学报， 1998(3)： 68-73．

[3]潘树来， 王全凤， 俞缙. 利用初流量法分析有自由面渗流问题之改进[J]. 岩土工程学报， 2012， 34(2)： 202-209．

[4]朱军， 刘光廷. 改进的单元渗透矩阵调整法求解无压渗流场[J]. 水利学报， 2001(8)： 49-52．

[5]王贤能， 黄润秋. 有自由面渗流分析的高斯点法[J]. 水文地质工程地质， 1997(6)： 1-4．

[6]陈昌禄， 潘文彦， 王晓章. 求解渗流自由面的变单元法[J]. 岩土工程技术， 2005， 19(4)： 166-169．

[7]李广信， 葛锦宏， 介玉新. 有自由面渗流的无单元法[J]. 清华大学学报： 自然科学版， 2002， 42(11)： 1552-1555．

[8]沈振中， 陈小虎， 吴越建. 求解堤坝渗流场的罚函数无单元法[J].河海大学学报：自然科学版，2008，26(1)：44-48．

[9]DARBANI M， OUAHSINE A， VILLON P， et al. Meshless method for shallow water equations with free surface flow[J]. Applied Mathematics and Computation， 2011(217)： 5113-5124．

[10]JIE Yuxin， LIU Lizhen， XU Wenjie， et al. Application of NEM in seepage analysis with a free surface[J]. Mathematics and Computers in Simulation， 2013(89)： 23-37．

[11]TANG Jing， LIU Yongbiao. Penalty Function Element Free Method to Solve Complex Seepage Field of Earth Fill Dam[C]. IERI Procedia， 2012(1)： 117-123．

[12]吴梦喜， 张雪勤. 有自由面渗流分析的虚单元法[J]. 水利学报， 1994(8)： 64-71．

[13]黄蔚， 刘迎曦， 周承芳. 三维无压渗流场的有限元算法研究[J]. 水利学报， 2001(6)： 33-36．

[14]苏枋， 王建祥， 热依汗. 丢弃单元法在三维有限元渗流分析中的应用[J]. 水力发电， 2009， 35(3)： 26-28.

(责任编辑 王 琪)

A Curve Fitting Method Based on Virtual Element Method for Solving Seepage Free Surface

SUN Weijian, HOU Xingmin, LI Yuandong, ZHENG Shanshan

(School of Civil Engineering, Yantai University, Yantai 264005, Shandong, China)

The seepage plays a key role in the stability and deformation of dam slope, so the free surface determination is one of main contents in seepage calculation. At present, the virtual element method is often used to solve this problem, but the method needs to adjust the element passing through the free surface continuously, which makes the iteration efficiency slow and causes the element deformity. A curve fitting method is proposed herein to obtain a high-accurate free surface without re-adjusting the elements. Practical engineering examples show that the method is efficient, stable and accurate．

seepage free surface; fixed grid method; FEA; virtual element method

2016-01-27

山东省自然科学基金资助项目(ZR2012EEL31)

孙伟建(1991—)，男，山东潍坊人，硕士研究生，主要从事岩土工程研究．

TV139.14

A

0559-9342(2016)11-0050-04