基于集对分析的马尔可夫链入库流量分布特征动态分析

李爱云，赵雪花

(太原理工大学水利科学与工程学院，山西太原030024)

基于集对分析的马尔可夫链入库流量分布特征动态分析

李爱云，赵雪花

(太原理工大学水利科学与工程学院，山西太原030024)

不确定性问题具有随时间动态变化，且具有多样性、变异性和复杂性及不精确性。其中许多不确定性问题呈现某种趋势的非平稳随机过程，即具有将来与过去无关的特性，而对这类问题的预测研究采用基于集对分析的马尔可夫链的动态预测模型。根据小浪底水库1919年～1974年的入库流量资料，应用有序样品聚类原理将入库流量分成枯水、偏枯、中水、偏丰、丰水5种等级区间；以各滞时步长马尔可夫链的集对权重，预测 1973年～ 1974年的入库流量，将其所在状态区间与实测值进行对比。结果表明，基于集对分析的马尔可夫链模型对小浪底水库入库流量预测精度较高。

集对分析；马尔可夫链；入库流量；马氏性检验

0 引 言

受到众多因素的影响，年径流预测具有很大的不确定性，且年径流的预测因子的结构是动态复杂的，其具有多样性、变异性及不精确性。长期以来，水文预测工作者依据大量的实测水文资料，努力尝试寻求水文资料的各种关系。包括：在时间演变过程中前后关系；与主要影响因素的关系；空间分布上各种要素的关系。通过这些关系以达到对水文资料的分析计算、预测、评价及决策[1-3]。马尔可夫于1907年提出的马尔可夫链预测方法，根据状态之间的转移概率来推算系统未来的发展趋势。Zekai Sen应用马尔可夫链对洪水来水情况进行预测[4-5]，预测结果合理可靠。本文应用集对分析原理分析原序列和各滞时后的序列之间的确定性和不确定性，提高马尔可夫链权重的确定，探讨集对分析与马尔可夫链的耦合动态预测模型。

1 基于集对分析的马尔可夫链动态预测模型[6]

1.1 步骤1——划分状态空间

先把样本序列从小到大进行排序，再根据有序样品聚类法的方法来划分入库流量变化区间，这样可以充分地考虑径流序列的数据结构。即确定了马尔可夫链的状态空间。其基本原理为：如果用数据x1，x2，…，xn表示N个有序的样品，则每一类一定是这样的形式：{xn，xn+1，…，xn+k}。其中，1≤n≤N，k≥0且n+k≤N。也就是同类样品一定是相互近邻的。有序聚类的Fisher的算法如下：把序列x1，x2，…，xn按某一归类{xn，…，xm}，m≥n。定义均值向量

(1)

式中，m(也称状态)为序列x的个数，m也称之为状态；n与n+k是属于N个有序样品的个数，但均小于N；k是滞时。

各变量间的差异性用以下面模型来衡量。即

(2)

式中，D(n，m)是分类的直径，其值的大小与段内变量之间的差异有关，其值越小表示段内变量的差异越小；反之，则表示差异越大。xt表示在t时刻的序列值。

1.2 步骤2——确定各滞时步长的集对权重

将n个有序变量分为f类，其分法为P(n，f)：{m1，m1+1，…，m2-1}； {m2，m2+1，…，m3-1}；…，{mK，mK+1，…，mn}。其分类误差为

(3)

L[P(n，f)]最小时就是最优分割法。f一般可以根据L[P(n，f)]和f的关系曲线图确定，曲线拐点处的f值即为最优分类数。

如原样本序列状态空间A=[x1,x2,…,xN]，则原样本序列滞时k指延迟的时间，亦即滞时步状态空间为Bk=[xk+1,xk+2,…,xN](k=1,2,…,K)。将集合A分别与集合Bk构成集对H(A,Bk)进行同异反分析，得出相应的联系度表达式。这里把研究对象分成5类，把元素处于同一等级的定义为相同，其个数是S；相差一级的(如Ⅰ与Ⅱ，Ⅱ与Ⅲ)定义为差异一，其个数是F1；相差两个等级(如Ⅰ与Ⅲ，Ⅱ与Ⅳ)的定义为差异二，其个数是F2；相差三个等级及其以上(如Ⅰ与Ⅳ，Ⅱ与Ⅴ)定义为相反，其个数是P，相应的联系数

(4)

式中，μk∈[-1,1]。为了求得指标权重，需要对联系数进行转换。即

Uk=0.5×μk+0.5

(5)

式中，Uk是相对联系数值，其取值范围为[0，1]。滞时k步的马尔可夫链的权重

(6)

式中，K为最大滞时阶数。

1.3 步骤3——马氏性检验

设为1步状态转移频率矩阵，于是

(7)

当N较大时，统计量

(8)

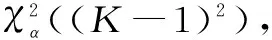
1.4 步骤4——预测概率

(9)

根据max{Pm|m=1,2,…,M}所对应的状态，作为该时段入库流量的预测状态。待该时段之后，将其带入到原来的序列之中，再重复以上步骤即可预测下时段指标值状态。

2 工程实例

现以1919年～1972年的资料预测1973年的入库流量，其步骤如下。

2.1 确定马尔可夫链的状态空间

把1919年1972年的入库流量(见表1)按从小到大的顺序排列，按最优分割法求出误差函数L[P(n，e]与分类数e关系(见图1)。根据图1，把入库流量分为5个等级区间比较合理(见表2)。

2.2 计算马尔可夫链的权重

按1.2确定各滞时步长的马尔可夫链的集对权重。由表2可得，原入库流量的状态序列A=[x1,x2,…,xN]分别与原入库流量k步滞时的状态序列Bk=[xk+1,xk+2,…,xN](k=1,2,…,K)构成集对

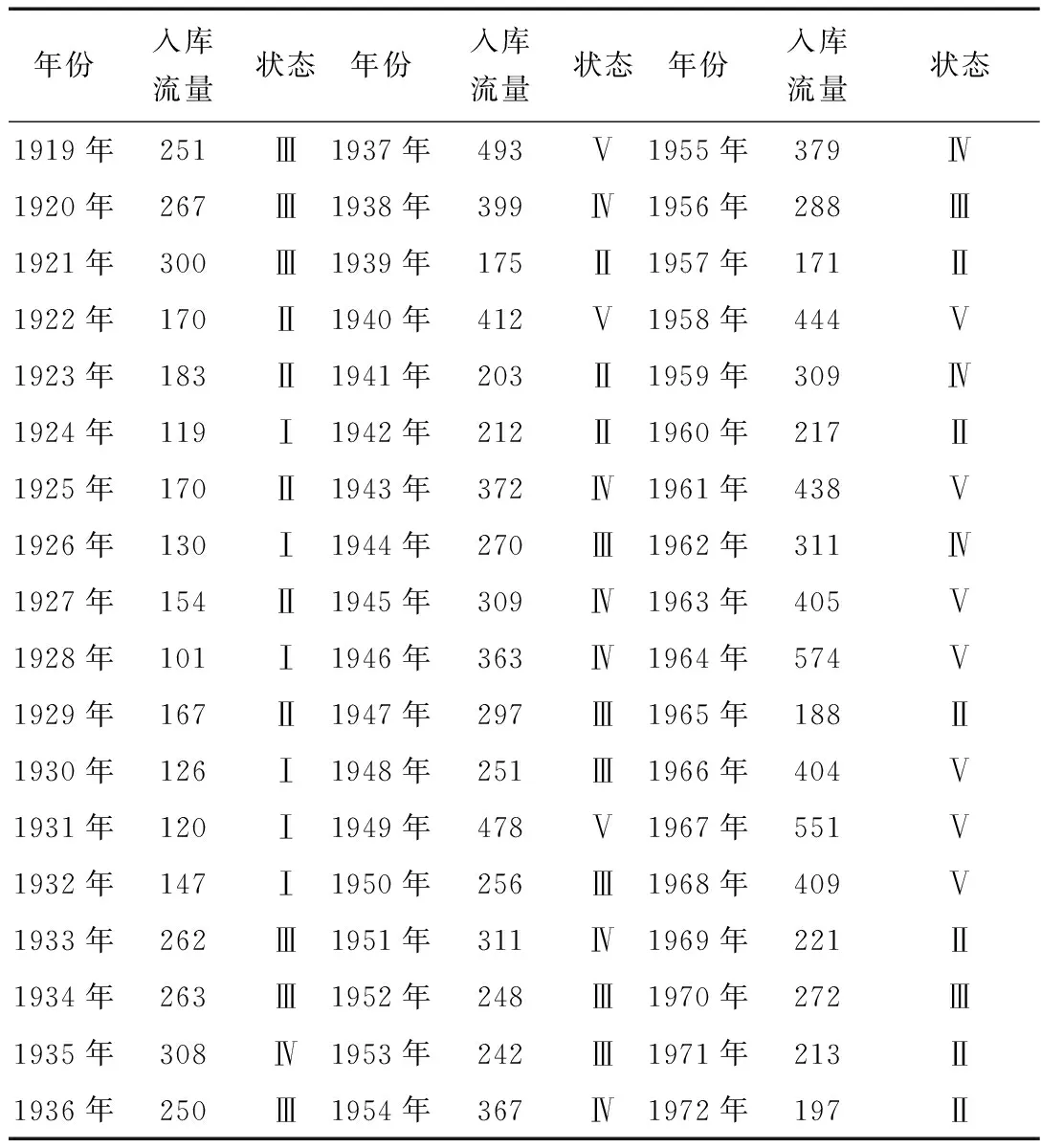
表1 1919年～1972年入库流量序列及状态 m3/s

图1 误差函数L[P(n，e)]与分类数e关系

表2 入库流量等级区间划分 m3/s

H(A,Bk)(k=1～5)进行同异反分析，得出相应的联系度表达式

μ1=0.3208+0.4151i1+0.1509i2+0.1132j

μ2=0.3269+0.3846i1+0.1731i2+0.1154j

μ3=0.3725+0.3333i1+0.1961i2+0.0981j

μ4=0.26+0.34i1+0.26i2+0.14j

依据经验，取i1=0.5，i2=-0.5，j=-1得出联系数Uk=(0.3397,0.3172,0.343,0.16,0.2245)，由式(5)得到相对联系度数值Uk=(0.6698,0.6586,0.6715,0.58,0.6122)，再根据式(6)得到各滞时步长的马尔可夫链的权重ωk=(0.2098,0.2063,0.2104,0.1817,0.1918)。

2.3 马氏性检验

通过统计得出各种步长的状态转移概率矩阵为

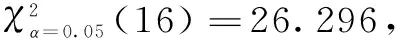
2.4 入库流量预测

根据1968年～1972年的入库流量及对应的状态转移矩阵对1973年的入库流量进行预测(见表3)。

将max{Pm}=0.343，这时m=2，也就是1973年的入库流量预测状态为Ⅱ为偏枯年(152≤X<226 m3/s)，与1973年的入库流量197 m3/s相吻合。

同理，以1969年～1973年的入库流量资料，按照上面的步骤预测1974年的年径流状态(见表4)。

将max{Pm}=0.313，这时m=2，也就是1974年的入库流量预测状态为Ⅱ为偏枯年(152≤X<226 m3/s)，与1974年的入库流量224 m3/s相吻合。

表3 1973年入库流量预测

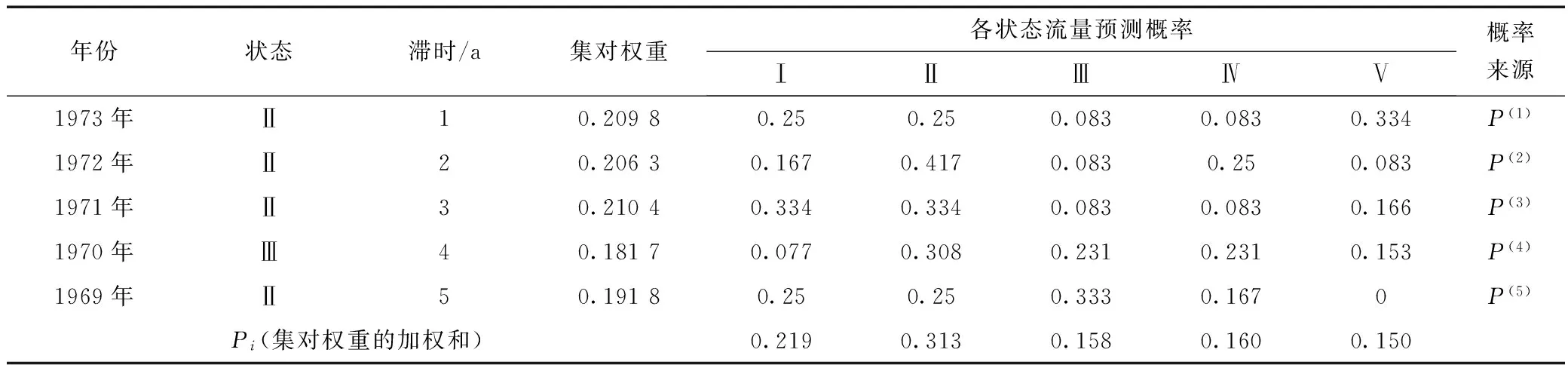
表4 1974年入库流量预测

2.5 各步长马尔可夫链的特性分析[7-8]

由于入库流量的马尔可夫链状态是相通的，即m↔n(m,n∈E,m≠n)，并且是非周期的，其全部状态构成一个闭集C，即为该链的状态空间E。通过分析该链是遍历的(非周期、不可约、正常返)。根据遍历原理，此链存在唯一的极限分布。即

(10)

利用小浪底水库1919年～1972年的资料，以相对联系度最大的步长为2的马尔可夫链的特性分析，应用公式(10)求出极限分布，并根据极限分布可以求出各状态的重现期，即Tm=1/πm，结果见表5。

表5 马尔可夫链的极限分布与各状态的重现期

由表5可见，各状态的重现期为T1=9.74，T2=4.33，T3=3.81，T4=4.75，T5=5.17。根据现有的实测资料，由本文有序样品聚类确定的分类标准及表5中的概率值分析，出现偏枯、中水和偏丰年的概率最大，总概率为0.704。

3 结 语

应用实例结果表明，基于集对马尔可夫链对入库流量分布特征进行动态分析可有效分析径流序列的内在规律，使划分的年径流区间更合理；由于集对权重的马尔可夫链预测模型能充分考虑到原序列状态和滞时k步后序列状态之间的确定及不确定关系，有利于提高预测精度。

[1]王文圣， 李跃清， 金菊良， 等. 水文水资源集对分析[M]. 北京： 科学出版社， 2010.

[2]覃光华， 宋克超， 周泽江， 等. 基于 WA-GRNN 模型的年径流预测[J]. 四川大学学报： 工程科学版， 2013.

[3]赵永龙， 丁晶. 相空间小波网络模型及其在水文中长期预测中的应用[J]. 水科学进展， 1998， 9(3)： 252-257.

[4]SEN Z. Critical Drought Analysis by Second Order Markov Chain[J]. Journal of Hydrology， 1990， 120(1-4)： 183-202.

[5]夏乐天， 马尔可夫链预测方法及其在水文序列中的应用[D]. 南京： 河海大学， 2005.

[6]汪明武， 金菊良， 周玉良. 集对分析耦合方法与应用[M]. 北京： 科学出版社， 2014.

[7]夏乐天， 梅雨强度的指数权马尔可夫链预测[J]. 水利学报， 2005， 36(8)： 988-993.

[8]潘刚， 芦冰， 邹兵， 等. 马尔可夫链在水库主汛期降雨状态预测中的应用[J]. 水利科技与经济， 2011， 17(6)： 33-36.

(责任编辑 陈 萍)

Dynamic Analysis of Inflow Distribution by Using Markov Chain Based on Set Pair Analysis

LI Aiyun, ZHAO Xuehua

(College of Water Conservancy, Taiyuan University of Technology, Taiyuan 030024, Shanxi, China)

The uncertainty has a dynamic process over time and it also has diversity, variability, complexity and imprecision. Many uncertainties present a trend of non-stationary random process, which has a feature of no relationship between future and past. For forecasting this type of uncertainty problem, the dynamic analysis model based on Markov Chain of Set Pair Analysis is used in here. According to the actual inflow data of Xiaolangdi Reservoir from 1919 to 1974, the principle of sequence sample cluster is used to divide the inflow sequence into five conditions, including drought, lean drought, normal, lean wet and wet, and then the inflow of Xiaolangdi Reservoir in 1973-1974 is forecasted by the set pair weights of Markov Chain with different lag time steps. The forecasting results are compared with actual measured data. The comparison shows that the Markov Chain model based on Set Pair Analysis can predict the inflow of Xiaolangdi Reservoir with higher precision．

Set Pair Analysis; Markov Chain; reservoir inflow; Markov property testing

2015-12-21

山西省科技攻关基金资助项目(20140313023-4)

李爱云(1977—)，女，山西阳泉人，讲师，硕士，主要从事水文预报研究与教学工作．

TV122.5

A

0559-9342(2016)11-0016-04