海平面上升引发的极端高水位的频率风险评估模型及其应用——以宁波为例

汪杨骏，张　韧，钱龙霞，葛珊珊，王　锋

(1.解放军理工大学 气象海洋学院，江苏 南京 211101；2.河北省唐山市曹妃甸工业区气象局，河北 唐山 063000 )



海平面上升引发的极端高水位的频率风险评估模型及其应用——以宁波为例

汪杨骏1，张韧1，钱龙霞1，葛珊珊1，王锋2

(1.解放军理工大学 气象海洋学院，江苏 南京 211101；2.河北省唐山市曹妃甸工业区气象局，河北 唐山 063000 )

摘要:海平面上升是全球变化研究的热点，海平面上升引发的极端高水位事件将严重威胁沿海城市的经济发展和社会生活。因此在当前气候变化背景下，开展极端高水位事件的风险评估显得尤为重要和迫切。对此引入频率风险思想，从极端高水位事件发生的频率、强度和造成的后果等角度构建了频率风险的概念模型和评价指标体系，建立了基于耿贝尔极值法、灰色Verhulst模型和ArcGIS平台的极端高水位频率风险评估模型；以浙江省宁波市为例，进行了气候变化情景下不同极端高水位发生频率对我国沿海城市遭受经济损失的风险评估实验。结果表明，基于国内外众多学者对我国极端高水位预估情景，2050年极端高水位事件的发生频率预期将远大于当前，沿海城市岸堤的防范能力较之目前将有大幅度的降低；并给出了不同强度的极端高水位事件对宁波市构成潜在威胁和经济损失风险的定量评估。

关键词:海平面上升；极端高水位；频率风险分析；耿贝尔极值法；灰色Verhulst模型；宁波

IPCC第五次报告指出自20世纪起海平面上升的速度在加快。到21世纪，在所有RCPs情境下，海平面上升的速率很可能都将超出1971-2010年的海平面上升速率，同时平均海平面上升将很可能致使未来城市沿岸极端高水位事件呈上升趋势[1]。沿海城市是世界上人口、经济和社会发展的重要区域和集聚中心，也是自然灾害易发和频发区域[2]。由于海平面上升，将缩短极端高水位重现时间，降低如机场、隧道等沿海基础设施的设计标高[3]。越来越多证据表明，极端高水位发生的频率和强度的增强是影响未来沿海城市社会经济体系正常运行的重大威胁。

近年来，日益严重的灾害问题已经引起政府和学术界的广泛关注，以救灾为主的灾后管理已经无法应对气候变化背景下未来不断增大的灾害损失和风险，开展有效的灾害风险评估与管理是沿海地区预防自然灾害、控制和降低灾害损失的重要基础性工作[4]。国内相关研究如下：基于历史典型洪水或不同重现期洪水情景开展分析，研究洪水发生的特征并评价其对城市造成的风险[5-7]，对未来极端高水位事件的强度或者频率的变化进行预测[8-11]。国外的研究侧重于对某一重现期内的极端高水位事件发生的综合风险进行评估,得到其对沿海城市整个社会经济系统造成的风险[12-14]。

综上所述，目前国内对于极端高水位事件风险的研究，比较侧重于过去极端高水位事件的分析或对未来极端高水位事件强度或频率的预测，对极端高水位事件产生的后果及风险，考虑相对不足。此外，对极端高水位事件危险性的分析，也多限于单一要素(或事件发生的频率或事件发生的强度)，综合考虑多风险要素，对事件进行较全面的频率风险分析、分析不同事件序列下，极端高水位事件的综合风险评估还较为欠缺。为此，本文选择受海平面上升引发的极端高水位事件影响严重的宁波作为典型案例，综合考虑极端高水位事件发生的频率、强度及产生的后果等要素，开展气候变化背景下极端高水位事件频率风险分析，探索气候变化区域响应的灾害风险理论分析方法、剖析典型案例，为我国沿海城市可持续发展和防范气候变化灾害提供科学依据和决策支持。

表1　频率风险指标体系

1频率风险指标与算法模型

频率风险分析(风险分析的频率方法)是一种对系统的安全性进行分析的有效途径；它不仅仅考虑最坏的受灾情况，还全面考虑可能的情形及相应后果，并使发生这些情形发生频率也成为合理定量处理不确定性的关键因素。频率风险可以定义为：导致破坏的事件序列(意外情况)、相应的频率和对应的结果。在这种观点中，风险分析的结果是一张不同情形发生的频率和后果的量化表，两者共同代表了风险[15]。因此，以极端高水位事件为例，频率风险是由不同极端高水位事件序列、发生的可能性以及其造成的后果综合作用而成。沿海地区海平面上升引发的极端高水位事件的频率风险指标体系如表1所示。

1.1　事件强度和频率

强度和频率是描述极端高水位事件的两个重要指标，其中，强度是极端高水位事件发生时的水位高度，用Z表示；频率是单位时间内，该极端事件发生的次数，用P表示。本文基于耿贝尔极值法计算极端高水位事件发生的频率，用参数估计法计算强度。

根据频率风险分析的定义，本文的极端高水位事件序列由极端高水位的强度表示，不同的极端高水位强度代表不同的极端高水位事件：

Z={z1，z2，z3…zn}。

(1)

1.2　事件后果C

后果是由暴露在灾害中的总资产及其脆弱性两部分组成。当极端高水位事件发生时，会对承灾体的社会经济体系造成危害。造成的后果不但与受灾区暴露在洪水中的总资产有关，而且与受灾区的地理位置有关。不同海拔高度的受灾区面对极端高水位事件时，其暴露在洪水中的资产所遭受的损失是不一致的，脆弱性函数可表示为：

V(Z-Y)=(Z-Y)/(Z-Y+1)。

(2)

式中：Z为极端高水位强度；Y为陆地高程。资产的脆弱性会随着给定的水位差的变化而发生变化。例如当水位差为1m时，暴露在极端高水位中的50%的资产会遭受损失[16]。

相关研究表明，一个城市居民的财产大致相当于一个城市年均GDP的5倍[17]，因此可将暴露性资产近似定义为：

A=Ps(Z-Y)×As×5 ρ×S(Y)×As×5。

(3)

式中：Ps为受灾人口；ρ为人口密度；S(Y)为某一路地高程上的面积，As为人均资产。

因此，极端高水位事件的后果可定义为：

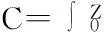
(4)

1.3　频率风险算法模型

综合上述频率风险指标，可得到频率风险的评估模型：

Risk=f(Z,V,C)=Pov×∫Z0V×AdY=

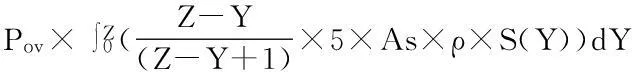
(5)

式中：Z={z1,z2,z3,…，zn}。

2极端高水位事件的频率风险评估模型

2.1　耿贝尔极值分布

耿贝尔[18]首次把Fisher-TippettⅠ型极值分布用于水文统计中，故称之为耿贝尔分布。由于耿贝尔分布形式简单，而且对海平面极值的拟合效果较好，故此采用耿贝尔分布方法研究由海平面上升引起的极端水位频率和强度变化，其表达式为：

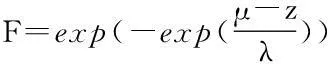
(6)

式中：μ为位置参数；λ为尺度参数。

2.1.1极端高水位频率

假设1：各极端高水位事件相互独立，且极端高水位事件发生次数的可能性服从泊松分布[19]，则

F=1-E=exp(-T/R)=exp(-N)。

(7)

式中:F为在一段时间内，海平面高度没有超过给定最高水位的频率。E为在一段时间内，海平面高度至少有一次超过给定最高水位的频率；T为重现期；R为发生超过给定最高水位事件的平均时间间隔；N为在一个给定时间，平均超出给定最高水位的事件次数。

将式(7)代入式(6)，则得

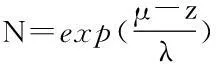
(8)

假设2：不同极端高水位事件发生的频率为PN，则极端高水位事件发生的频率期望NE是

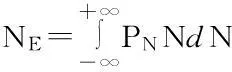
(9)

假设3：尺度参数λ不随海平面的上升而改变。在一段时间T内，当N=1时，μ=z。令海平面高度z=z0+Δz+z′。其中z0是一段时间内海平面高度平均值，Δz+z′是未来预估的平均海平面上升高度，其中Δz为预估的中心值，z′为围绕零值的随机分布函数。则

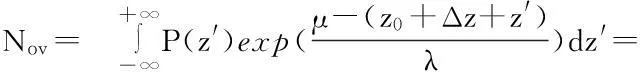
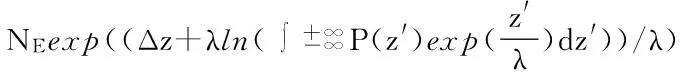
(10)

式中：Nov即为未来极端高水位发生次数。

2.1.2极端高水位强度

设一组极端高水位最高潮位的历史数据X={x1,x2,…,xn}，用矩估计法[20]可以拟合得到耿贝尔分布的尺度参数和位置参数。

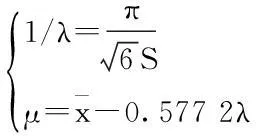
(11)

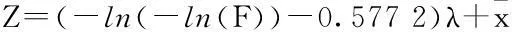
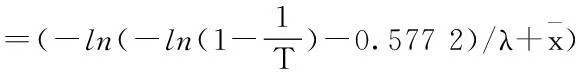
(12)

式中：Z即为未来极端高水位发生强度(水位)序列，T={t1,t2，…,tn}。

2.2　灰色Verhulst模型

灰色系统理论是一种研究少数据、贫信息不确定性问题的新方法。灰色系统理论以“部分信息已知，部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象，主要通过对“部分”已知信息的生成、开发来提取有价值的信息，实现对系统运行行为、演化规律的正确描述和有效监控。灰色Verhulst模型主要是用来研究具有饱和状态S型序列的，而人口和人均GDP随时间的变化曲线符合此规律[21]。因此，引入灰色Verhulst模型来预测宁波市的人口和人均GDP水平[22]。

2.2.1灰色Verhulst预测模型

设在一个模型预测中，原始数列：x(1)=(x(1),x(1)(2),x(1)(3),…,x(1)(n))，为了弱化呈离散状态的原始数据，对原始时间序列做一次累减，经过处理的时间序列称为累减序列：x(0)=(x(0)(1),x(0)(2),x(0)(3),…,x(0)(n))；然后通过对原始数据序列累加生成的递增序列实行紧邻均值生成z(1)。定义数据矩阵：

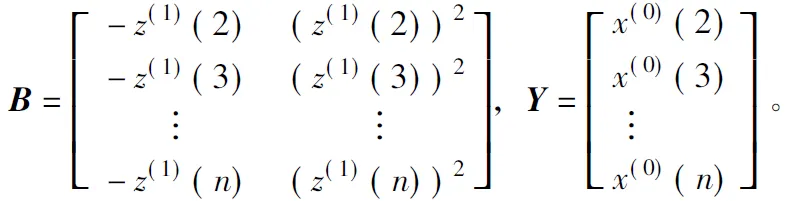
计算参数

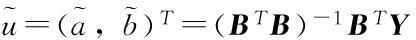
(13)

式中：符号~表示估计值。则Verhulst模型的白化方程为：

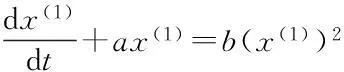
(14)

2.2.2灰色Verhulst预测模型求解

解式(14)得：

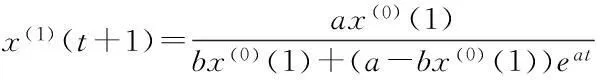
(15)

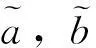
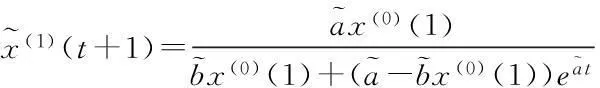
(16)

最后对模型进行检验，得到人口密度ρ和人均GDP As的预估值。

2.3　ArcGIS地理信息系统

地理信息系统(GIS)利用利用计算机建立地理数据库，将空间地理分布状况及所具有的属性进行数字存储，建立数据管理系统，同时开发各种分析和处理功能，以便快速获取信息，并将处理结果以地图、图形及数据的形式表示出来。GIS的核心是管理、计算、分析地理坐标位置信息及相关位置上属性信息的数据库系统。本文引入ArcGIS平台，基于DEM数字高程数据,对研究区数字高程数据和风暴潮水位基准数据进行坐标系统匹配和高程基准转化。匹配后二者均以WGS84坐标系统为水平基准面,以吴淞高程为零基准面。通过“空间分析”中 “地图代数”中的“栅格计算器”计算出不同陆地高程包含的城市面积，拟合得到宁波市的“高程——面积”函数S(Y)。

3基于气候变化情景的风险评估

3.1　研究区概况

浙江省宁波市位于东海之滨，陆域总面积达9 816 km2，坐拥漫长的海岸线，但市区平均海拔不到6 m，易受到海平面上升的影响引发风暴潮，极端高水位等自然灾害。截止到2013年末，全市拥有户籍人口580.1万，实现地区生产总值(GDP)7 100亿元，作为浙江省第一大工业城市，对其受极端高水位灾害的损失情况进行风险评估，有一定的代表性和实用性。

3.2　宁波市极端高水位风险评估

3.2.1模型可靠性分析

为检验模型的可靠性，探讨该模型对于2050年宁波市所遭受的极端高水位事件的风险评估结果的实用价值，本文结合宁波水文站发布的《水情年报》和国家海洋局发布的《中国海洋灾害公报》得到历年极端高水位事件发生的时间、强度以及造成的实际经济损失，再根据极端高水位发生年份宁波市人口和人均生产总值数据，得到评估模型模拟的经济损失如表2所示。

表2　宁波市极端高水位事件经济损失模拟数据与实际数据对比

通过表2可知，该风险评估模型模拟的历年极端高水位事件经济损失与实际经济损失非常接近，其模拟结果是可信的，因此可以利用该模型进行下一步的分析。

3.2.22050年极端高水位发生的频率和强度

首先构建正态分布模型，将2050年中国海平面上升不同的预估结果(表3)代入式(17)，以模拟未来海平面上升的总体情况[23]。并对该模型作Kolmogorov-Smirnov检验，检验结果见表4，模型中各变量的相关统计量见表5。

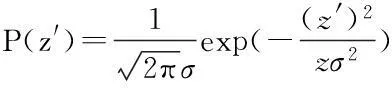
(17)

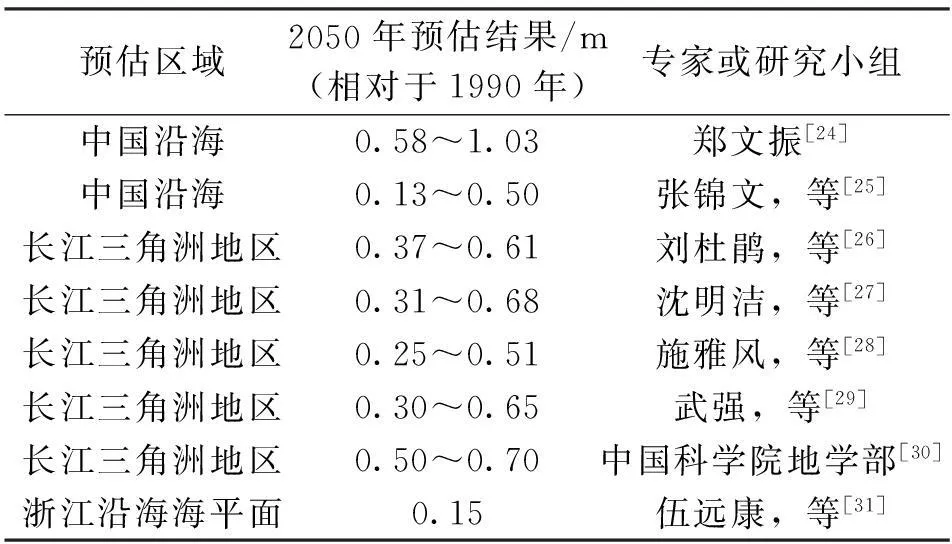
表3　中国沿海未来海平面变化的预估成果

表4　K-S检验结果

表5　最终模型统计量

由表3可知，Kolmogorov-Smirnov检验的P值落在置信区间内，检验通过，接受原假设，即未来中国海平面上升的总体情况符合正态分布。将式(17)代入(10)得：

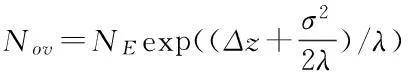
(18)

将表5中各变量代入式(18)得Nov=44.5NE，其中尺度参数λ=0.1718m，是由宁波水文站所得1950-2006年宁波历史最高潮位数据代入(11)所得。因此2050年，极端高水位发生的频率为：

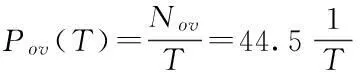
(19)

式中：T={t1,t2,…,tn}，由式(12)得，2050年极端高水位事件发生的强度为：

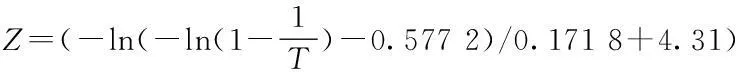
(20)

3.2.32050年平均人口密度和人均GDP

(1)用灰色Verhulst模型对1997-2013年的人口密度和人均GDP的时间序列(数据资源来自宁波统计局)进行重构并检验精度；

(2)对于人均GDP模型的检验：C=0.103 0，P=1;根据表6得到该模型属于第Ⅰ精度，可以进行长期预测；

(3)对于人口密度模型的检验：C=0.177 6，P=1;根据表6得到该模型属于第Ⅰ精度，可以进行长期预测。

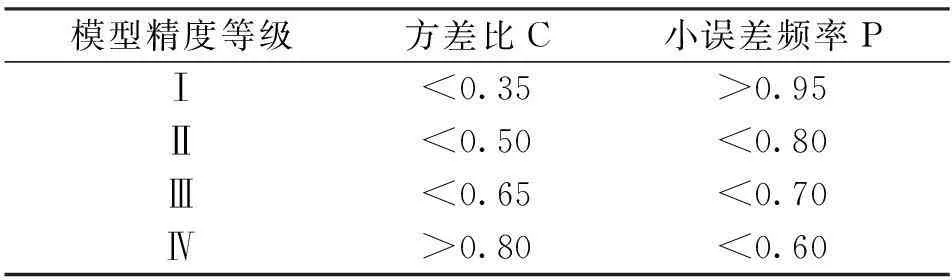
表6　模型精度表

于是，采用灰色Verhulst模型对未来进行预测。

根据图1，可拟合得到未来2050年的人均GDP(As)估算为26.366万元。人口密度(ρ)估算为679人/km2。

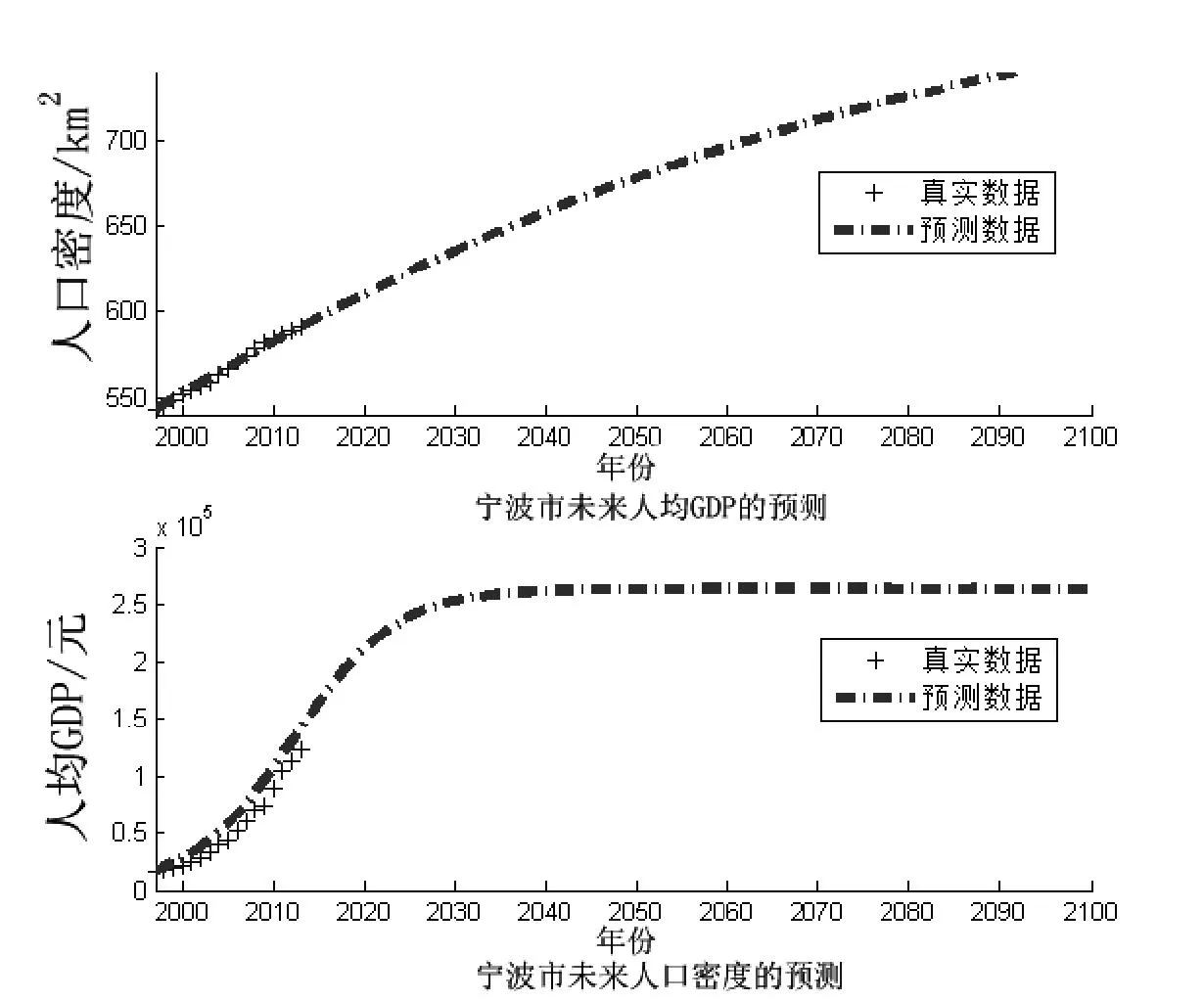
图1　宁波市未来人口经济状况预测

3.2.4宁波市路面高程-面积关系

通过ArcGIS地理信息系统提取宁波市的数字高程图模型，计算得到不同陆地高程与所其包含的面积如图2所示，通过拟合得到高程-面积函数表达式(1)。

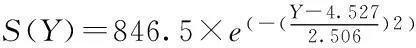
(21)

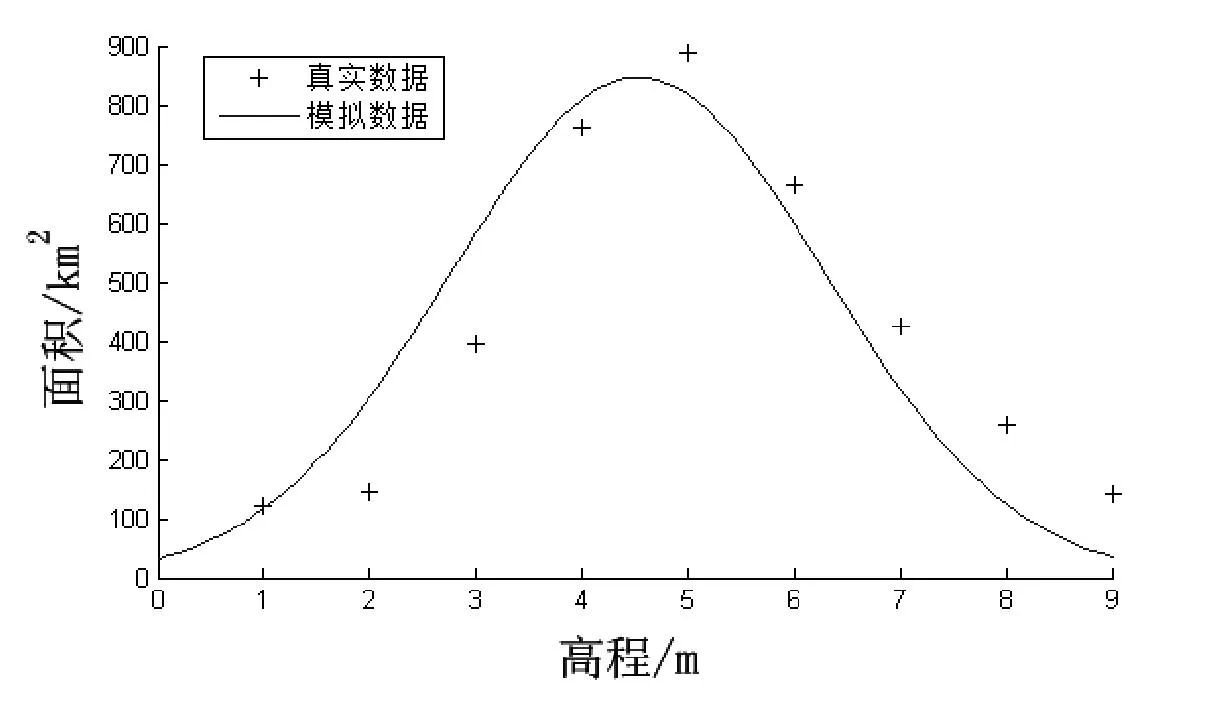
图2　宁波市路面高程-面积关系

3.2.52050年极端高水位风险

联立式(5)、式(19)、式(20)、式(21)得到极端高水位事件风险模型：

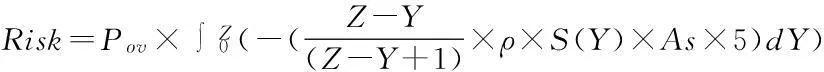
(22)

将Pov，As，ρ，S(Y)代入上式，则

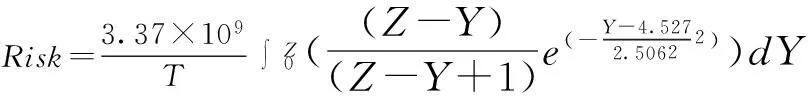
(23)

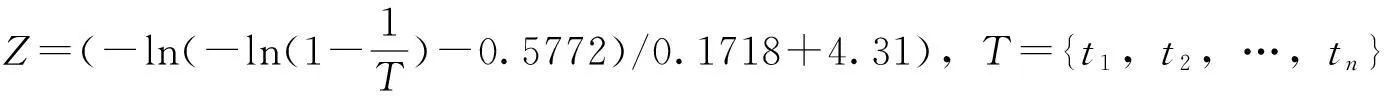
查阅宁波水文站资料得到，当前宁波市的保证水位平均值为4.38 m，若极端高水位超出4.38 m则会造成灾情。2050年宁波市极端高水位事件频率与强度分布情况如图3所示，在不加固任何岸防措施的情况下，超出保证水位的极端高水位事件强度和频率由图3中阴影部分表示。结果显示，气候变化背景下，估计2050年后宁波市年均至少发生11次强度超过保证水位的极端高水位事件，重现期一年的极端高水位事件强度可达5.06 m。

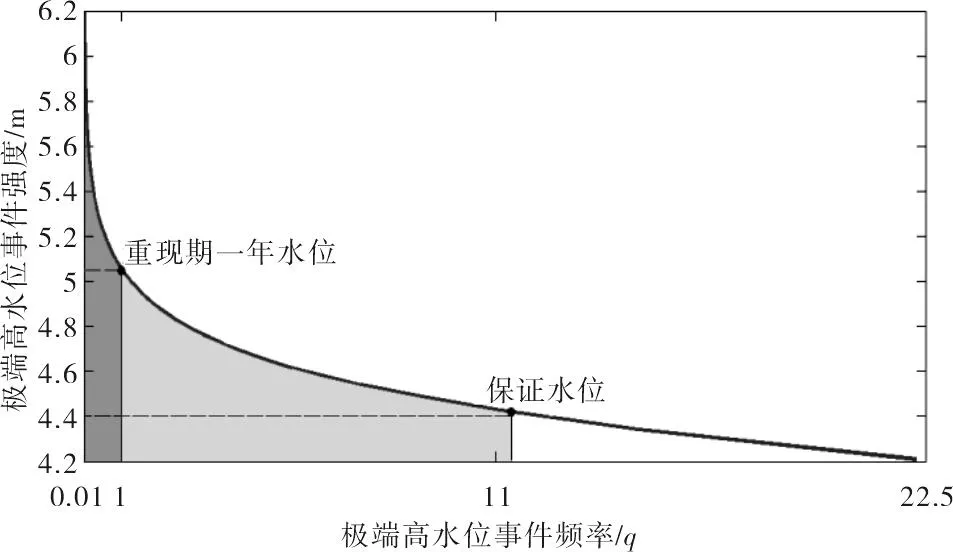
图3　宁波市2050年极端高水位事件频率-强度分布

风险就是频率和后果的乘积。图4阴影部分面积代表宁波市在2050年若不采取任何的措施加固加高岸防提高保证水位情形下，不同极端高水位事件年均可能造成的风险。图4中的频率风险模型分析，2050年，仅一次强度达到保证水位的极端高水位事件便可对宁波市造成约3 200亿元的经济损失，且强度达到保证水位的极端高水位事件对该市的风险最大。

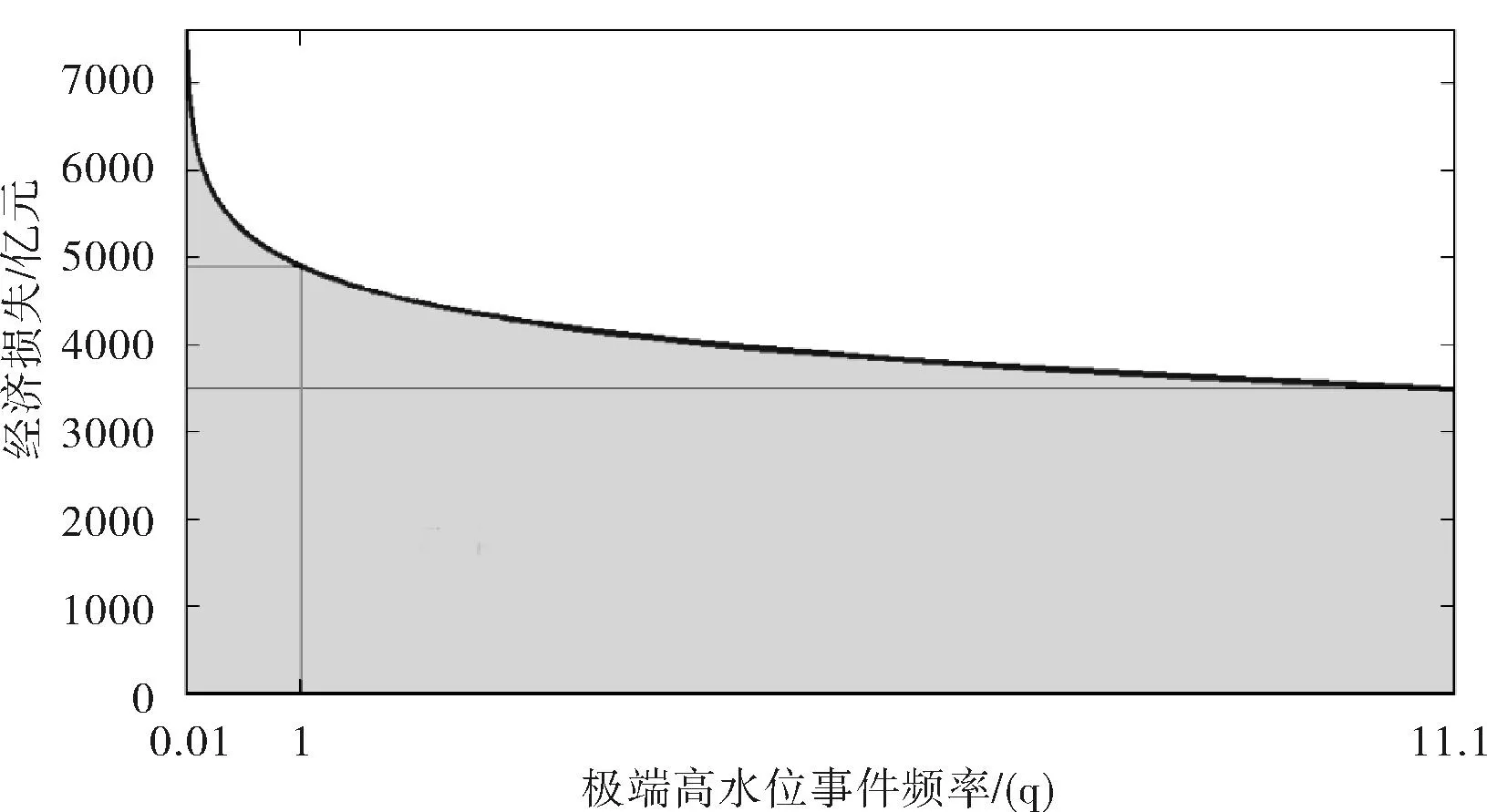
图4　宁波市2050年频率风险分析

4结论

(1)引入频率风险分析思想，从极端高水位事件的强度、频率和后果的角度建立了较为系统的极端高水位事件的频率风险分析指标体系和频率风险算法模型。

(2)利用耿贝尔极值法模拟了极端高水位事件发生的强度和频率，结合灰色预测理论和ArcGIS平台，建立了极端高水位事件的频率风险评估模型。

(3)针对气候变化背景下，2050年海平面上升，对宁波市极端高水位事件发生频率及其岸堤抵御极端高水位事件的能力和经济损失进行了情景预估。

(4)研究思想和技术途径旨在为我国沿海地区抵御和防范气候变化极端事件和灾害风险，提供科学参考。

参考文献：

[1]IPCC.Climatechange2013:thephysicalsciencebasis[M/OL].Cambridge:CambridgeUniversityPress,inpress, (2013)[2014-05-06].http://www.ipcc.ch/report/ar5/wg1/.

[2]谢翠娜. 上海沿海地区台风风暴潮灾害情景模拟及风险评估[D]. 上海：华东师范大学, 2010.

[3]BeckerAH,AcciaroM,AsariotisR,etal.Anoteonclimatechangeadaptationforseaports:achallengeforglobalports,achallengeforglobalsociety[J].ClimaticChange, 2013, 120(4):683-695.

[4]许世远, 王军, 石纯, 等. 沿海地区自然灾害风险研究[J]. 地理学报, 2006, 61(2): 127-138.

[5]杨佩国, 杨勤业, 吴绍洪, 等. 基于数值模拟的黄河下游不同情景溃堤洪水特征[J]. 地理研究, 2007, 26(2): 328-336.

[6]夏富强, 康相武, 吴绍洪, 等. 黄河下游不同洪水情景决溢风险评价[J]. 地理研究, 2008, 27(1): 229-239.

[7]赵庆良, 王军, 许世远, 等. 沿海城市社区暴雨洪水风险评价: 以温州龙湾区为例[J]. 地理研究, 2010, 29(4): 665-674.

[8]殷杰,尹占娥,于大鹏,等. 海平面上升背景下黄浦江极端风暴洪水危险性分析[J]. 地理研究, 2013,12:2215-2221.

[9]宗虎城, 章卫胜, 张金善. 海平面上升对黄浦江风暴潮水位影响研究[J]. 人民长江, 2014,45(9)：1-7.

[10]宋美钰, 王福, 王宏. 21世纪中叶天津沿海地区极端高水位趋势预测[J]. 地质通报, 2008, 27(6):829-836.

[11]董胜, 徐海博. 滩海地区风暴增水的季节变化对极端高水位确定的影响[C]// 2006年度海洋工程学术会议.北京，2006.

[12]FlatherR,BakerT,WoodworthP,etal.Integratedeffectsofclimatechangeoncoastalextremesealevels[C]//ProudmanOceanographicLaboratory.InternalDocumentNo. 140,Bidston,UK， 2001.

[13]LoweJA,GregoryJM,FlatherRA.ChangesintheoccurrenceofstormsurgesaroundtheUnitedKingdomunderafutureclimatescenariousingadynamicstormsurgemodeldrivenbytheHadleyCentreclimatemodels[J].ClimateDynamics, 2001, 18(3/4):179-188.

[14]HansonS,andNichollsRJ,Extremefloodeventsandportcitiesthroughthetwenty-firstcentury[C]//AsariotisR,BenemaraH.Maritimetransportandtheclimatechangechallenge.NewYork：Earthscan/Routledge, 2012:243.

[15]EnricoZio，翟庆庆. 可靠性与风险分析蒙特卡罗方法[M]. 北京：国防工业出版社，2014：9-10.

[16]HinkelJ,LinckeD,VafeidisAT,etal.Coastalflooddamageandadaptationcostsunder21stcenturysea-levelrise[J].ProceedingsoftheNationalAcademyofScience, 2014, 111(9):3292-3297.

[17]HansonS,NichollsR,RangerN,etal.Aglobalrankingofportcitieswithhighexposuretoclimateextremes[J].ClimaticChange, 2011, 104(1):89-111.

[18]BNnkHWVD,KönnenGP.Estimating10000-yearreturnvaluesfromshorttimeseries[J].InternationalJournalofClimatology, 2011, 31(1):115-126.

[19]PughDT.Tides,surgesandmeansea-level[J].Physics&ChemistryoftheEarthPartASolidEarth&Geodesy, 1987, 25(1):53-56.

[20]候瑞科. 利用耿贝尔极值分布计算年最高水位[J]. 海洋通报, 1993,12(3):126-129.

[21]胡泊. 灰色verhulst模型在长春市人口预测中的应用[J]. 经济视角, 2009, 12(6):21-23.

[22]卓金武.MATLAB在数学建模中的应用[M]//MATLAB在数学建模中的应用. 北京：北京航空航天大学出版社, 2014：65-66．

[23]GeorgeABackus,ThomasSLowry,WarrenDE.Thenear-termriskofclimateuncertaintyamongtheU.S.states[J].ClimaticChange, 2013, 116(3/4):495-522.

[24]郑文振. 全球和我国近海验潮站及任意地点(区)的21世纪海平面预测[J]. 海洋通报, 1996, 15(6):1-7.

[25]张锦文, 王喜亭, 王惠. 未来中国沿海海平面上升趋势估计[J]. 测绘通报, 2001, 18(4):4-5.

[26]刘杜娟, 叶银灿. 长江三角洲地区的相对海平面上升与地面沉降[J]. 地质灾害与环境保护, 2005, 16(4):400-404.

[27]沈明洁, 谢志仁, 朱诚. 中国东部全新世以来海面波动特征探讨[J]. 地球科学进展, 2002, 17(5):886-894.

[28]施雅风, 朱季文, 谢志仁,等. 长江三角洲及毗连地区海平面上升影响预测与防治对策[J]. 中国科学(D辑:地球科学)， 2000，30(3):225-32.

[29]武强, 郑铣鑫, 应玉飞,等. 21世纪中国沿海地区相对海平面上升及其防治策略[J]. 中国科学, 2002, 32(9):760-766.

[30]中国科学院地学部. 海平面上升对我国沿海地区经济发展的影响与对策[J]. 地球科学进展, 1993，8(6):15-25.

[31]伍远康, 汪邦道. 浙江省沿海海平面上升及预测[J]. 浙江水利科技, 2003, 12(2):1-4.

Model for Probabilistic Risk Assessment in Extreme High Water Level Caused by Rising Sea Level and Its Application——A Case Study in Ningbo

Wang Yangjun1, Zhang Ren1, Qian Longxia1, Ge Shanshan1and Wang Feng2

(1.InstituteofMeteorology,PLAUniversityofScienceandTechnology,Nanjing211101,China;

2.MeteorologicalBureauofCaofeidianIndustrialZone,Tangshan063000,China)

Abstract:Sea level rise, which is a focus topic of global change study, will cause extreme high water level events bringing a series threat to the coastal city of economic development and social life. Therefore, in the background of the current climate change, we carry out risk assessment of extreme high water level events is particularly important and urgent. We introduce frequency risk ideology to construct frequency risk model and evolution index system containing frequency. Intensity and consequences of the extreme high water events. We established this model based on Gumbel extremum method, grey Verhulst model and ArcGIS platform, taking Ningbo city as an example to study the risk of the economic losses which China’s coastal city has suffered under different extreme high water level scenarios with the climate change. The results show that the occurrence frequency of extreme high water level events will be far greater than the current bank coastal city based on many domestic and foreign scholars’ predicting; the prevention ability will be greatly reduced. we also give the quantitative assessment of different extreme high water level events’potential threats to Ningbo and its economic losses.

Key words:sea level rise; extreme high water level; risk analysis of frequency; Geng Baer extremum method; grey Verhulst model; Ningbo

通讯作者：张韧(1963-)，男，四川峨眉人，教授、博士生导师，从事海洋环境影响评估与决策研究.E-mail: zrpaper@163.com

作者简介：汪杨骏(1990-)，男，浙江湖州人，硕士研究生，从事海洋环境风险评估研究.E-mail：492670449@qq.com

基金项目：国家自然科学 (41276088)；唐山市曹妃甸工业区专项课题(CQZ-2014001)

收稿日期：2015-05-12修回日期：2015-07-06

中图分类号：X43

文献标志码：A

文章编号：1000-811X(2016)01-0213-06

doi:10.3969/j.issn.1000-811X.2016.01.039