基于R软件实现随机抽样及其应用

张效嘉，胡良平,2*

(1.军事医学科学院生物医学统计学咨询中心，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029

基于R软件实现随机抽样及其应用

张效嘉1，胡良平1,2*

(1.军事医学科学院生物医学统计学咨询中心，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029

本文的目的是使读者快速掌握用R软件产生服从多种分布规律的随机数和多种随机抽样的方法。通过介绍随机数生成器的概念、对应的函数、实际生成服从正态分布和均匀分布的随机数，读者很容易获得基于R软件产生所需要的随机数；通过介绍有放回与无放回随机抽样、系统与分层随机抽样、整群与bootstrap随机抽样的概念和具体实现，使读者轻松地基于R软件实现多种随机抽样。事实表明：R软件易于获取、易学易用；R软件功能强大、适用面宽，可方便快捷地解决试验设计中的随机抽样问题。

R软件；随机数生成器；正态分布；均匀分布；随机抽样；bootstrap随机抽样

1 产生随机数[1-3]

1.1 随机数及其种类

1.1.1 概述

所谓随机数，就是它们在数量大小和先后顺序等方面，出现的规律是不确定的。然而，人们还可以在一定的前提条件限制下，去生成一系列的随机数，它们出现的先后顺序是随机的，但它们在整体上却是服从某种特定规律的。

由此可知，当人们将“前提条件”设定为“均匀分布”，就可生成均匀分布随机数；当人们将“前提条件”设定为“正态分布”，就可生成正态分布随机数；……；以此类推，还可生成很多服从其他特定分布规律的随机数。

1.1.2 随机数生成器种类

在计算机上，生成随机数需要基于一定的算法。不同的算法会生成不同的随机数。R提供了多种随机数生成器(random number generators，RNG)，默认的RNG是由Makoto Matsumoto与Takuji Nishimura于1997年-1998年提出的RNG，即Mersenne twister随机数生成器。该RNG的循环周期为219937-1。R还提供了其他几种RNG，通过在R的控制台发送命令“help(RNGkind)”，可以获得有关的详细信息。

若用户想把默认的RNG更改为自己指定的某种其他的RNG，可通过在R的控制台发送命令“RNGkind(kind=“new_rng”)”。注意：这里的“new_rng”只能是下列几种备选内容：Mersenne(默认项)、Wich、Mars、Super、Knuth-TAOCP-2002、Knuth-TAOCP、L’Ecuyer-CMRG。

1.1.3 确保每批生成的随机数相同

一般来说，生成随机数的函数每批生成的随机数是不同的。但有时，人们需要生成相同批次的随机数(如在临床试验设计和模拟试验时)，此时，可以在运行某种随机数函数时，先运行一下set.seed(n)函数(这里n为一个确定的正整数，如1或2等)。

现以生成均匀分布随机数的runif( )函数为例，在运行此随机数函数之前先运行set.seed( )函数，可使runif( )函数每批生成的随机数相同(生成的随机数的长度应相同)。

> set.seed(1)

> runif(10)

以上为第一次运行，要求生成在[0,1]区间内且服从均匀分布的10个随机数。

[1] 0.26550866 0.37212390 0.57285336 0.90820779 0.20168193 0.89838968

[7] 0.94467527 0.66079779 0.62911404 0.06178627

以上是第一次运行输出的10个随机数。

> set.seed(1)

> runif(10)

以上为第二次运行，仍要求生成在[0,1]区间内且服从均匀分布的10个随机数(与前面的10个随机数完全相同，此处从略)。

显然，以上两次运行，生成的在[0,1]区间内且服从均匀分布的10个随机数完全相同。

1.2 用R生成正态分布随机数

【例1】试生成100个服从均值为0、标准差为1的标准正态分布的随机数。

解答：在R中，使用rnorm( )函数可以生成服从正态分布的随机数。其语法规则是：rnorm(n,mean=k1,sd=k2)，其中，参数n代表需要生成的随机数的个数、k1为用户指定的均值、k2为用户指定的标准差。当k1=0、k2=1时，就是希望生成服从标准正态分布的n(n必须为一个具体的正整数)个随机数。rnorm(n,mean=0,sd=1)=rnorm(n,0,1)=rnorm(n)。

> r_number1<- rnorm(100,0,1);r_number1

以上语句的目的是生成100个服从均值=0、标准差=1的标准正态分布的随机数并将其赋值给变量(本质上是一个向量)r_number，然后，将其输出(输出结果从略)。

1.3 用R生成均匀分布随机数

在R中，使用runif( )函数可以生成服从均匀分布的随机数。其语法规则是：runif(n,min=k1,max=k2)，其中，参数n代表需要生成的随机数的个数、k1为用户指定的服从均匀分布的随机数的下限、k2为用户指定的服从均匀分布的随机数的上限。若省略参数min、max，则默认生成[0,1]上的均匀分布随机数。

【例2】试生成1000个服从下限为2、上限为12的均匀分布的随机数，并用直方图展示它们。

解答：为实现题中的目标，可使用下面的语句。

> x<- runif(1000,min=2,max=12)

> hist(x,prob=T,main="uniform distribution(min=2,max=12)")

第一句的目的是生成1000个服从下限为2、上限为12的均匀分布的随机数。

第二句的目的是绘制这1000个随机数的直方图(无法绘制非标准均匀分布密度函数曲线)。产生的直方图从略。

1.4 用R生成其他分布随机数

1.4.1 生成指数分布随机数

生成指数分布随机数的函数为rexp()，其语法规则是：rexp(n,lamda=1/mean)，这里n代表生成的随机数的个数，而lamda代表随机数的平均值的倒数，mean代表随机数的平均数。

> x<- rexp(1000,1/110);x

以上语句的目的是生成1000个服从均值为110的指数分布的随机数并将其输出(输出结果此处从略)。

1.4.2 生成贝塔分布随机数

生成贝塔分布随机数的函数为rbeta()，其语法规则是：rbeta(n,a,b)，这里，n代表生成的随机数的个数，而a和b代表该分布的两个非负的实数(a>0，b>0)。

> x<- rbeta(100,2,8);x

以上语句的目的是生成100个服从参数a=2、参数b=8的贝塔分布的随机数并将其输出(输出结果此处从略)。

1.4.3 生成伽玛分布随机数

生成伽玛分布随机数的函数为rgamma()，其语法规则是：rgamma(n,shape,rate=1,scale=1/rate)，这里，n代表生成的随机数的个数，而shape代表该分布的形状参数、scale代表尺度参数，这两个参数都应该为非负实数(shape>0、scale>0)。注意：rate与scale两个中只能给定一个的具体值。

> x<- rgamma(100,1,4);x

以上语句的目的是生成100个服从形状参数shape=1、尺度参数scale=1/4的伽玛分布的随机数并将其输出(输出结果此处从略)。

说明：在R中，还可生成许多服从其他分布的随机数，因篇幅所限，此处从略。

2 随机抽样[1-4]

2.1 概述

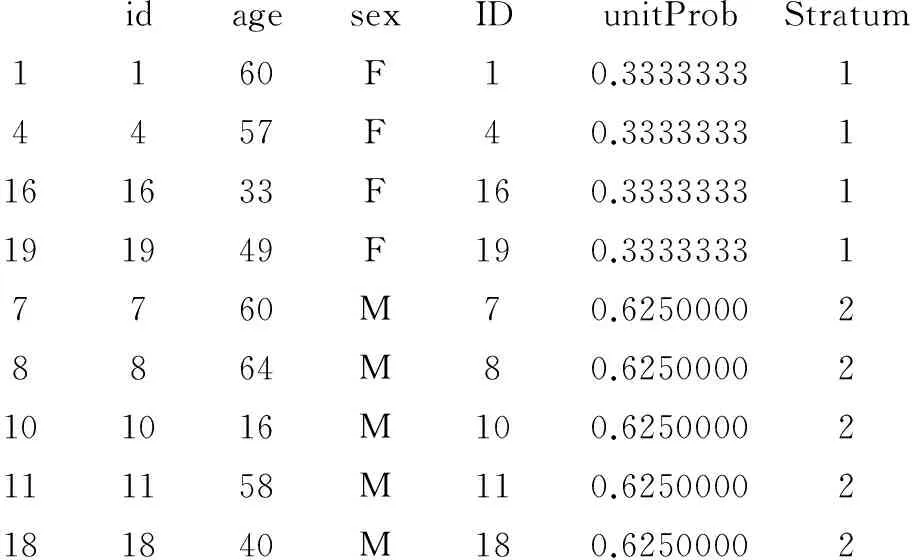
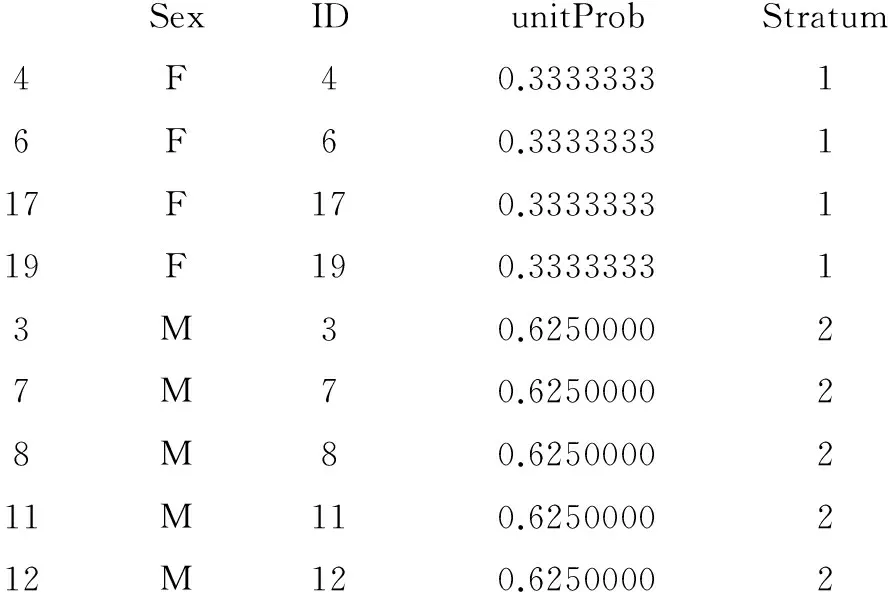
从给定的一个总体中抽取一定数目的样品，称为抽样。若总体中的所有样品被放在一个黑色的袋子中，样品的形状、大小、颜色和重量是相同的，只是上面的编号不同。当人们从中抽取若干个样品时，就称为随机抽样。这里的“随机”是指被抽取的样品是哪些，事先是不知道的。若从n个样品(假定它们构成一个总体)中一次性抽取m(m

在R中，可以使用sample( )函数来实现无放回与有放回随机抽样。其语法规则如下：

Sample(x,n,replace=F或T，prob=NULL)

x代表总体向量，可以是数据、字符、逻辑向量；n代表样本含量；replace=F，代表无放回随机抽样(这是默认的)，replace=T，代表有放回随机抽样；prob可以设置各个抽样单元不同的入样概率，进行不等概率抽样。

2.2 有放回随机抽样举例

【例3】假定掷一枚质地均匀的硬币，出现正面用“H”表示、出现反面用“B”表示，现重复抛硬币20次，显示有放回随机抽样的结果。

解答：在R中使用下面的语句就可实现前述的目的。

> sample(c("B","H"),20,rep=T)

[1] "B""B""H""B""H""B""H""B""H""H""B""H""B""H""H""H""H""H"

[19] "B""B"

以上是20次试验的结果，每次试验的结果要么是“B”、要么是“H”。其中，“B”出现了9次、“H”出现了11次。

【例4】假定掷一枚质地均匀的骰子(6个面上分别有1、2、3、4、5、6个点)，现重复抛骰子20次，显示有放回随机抽样的结果。

解答：在R中使用下面的语句就可实现前述的目的。

> sample(c(1:6),20,rep=T)

[1] 3 2 4 1 5 1 6 1 6 4 3 6 3 6 5 6 4 4 2 2

以上是20次试验的结果，每次试验的结果是1到6六个数字中的一个出现。这批试验的结果表明，1出现了3次、2出现了3次、3出现了3次、4出现了4次、5出现了2次、6出现了4次。

2.3 无放回随机抽样举例

【例5】现有编号为1～200的200位受试对象，希望从中随机抽取20位。试显示被随机抽取的20位受试者的编号。

解答：在R中使用下面的语句就可实现前述的目的。

> sample(200,20,rep=F)

[1] 180 47 91 124 22 141 36 186 193 8 53 67 113 68 154 143 108 59

[19] 123 71

以上是从1～200个编号中无放回地随机抽取的20个编号。

2.4 系统随机抽样举例

在R中，要想实现分层随机抽样或整群随机抽样，需要从R软件中下载sampling包，分别调用其中的strata( )函数与cluster( )函数；与此同时，这个包中还有getdata( )函数，可以读取随机抽样的全部样品对应的全部信息(否则，只有与抽样有关的部分信息)。

但是在R中，笔者目前尚未找到专门用于系统随机抽样的函数。虽然在下面的分层随机抽样的strata( )函数与整群随机抽样的cluster( )函数中，都涉及一个参数，即“method=”， 在等号后面可以输入四种抽样方法之一，即srswor(无放回随机抽样)、srswr(有放回随机抽样)、poisson(泊松随机抽样)和systematic(系统随机抽样)，但这四种具体的抽样方法都是在前面的分层随机抽样或整群随机抽样基础之上的，而不是直接实施这四种具体随机抽样的。故此处暂不能进行系统随机抽样，若用户今后从R软件中发现了某个包中的某些函数可直接进行系统随机抽样或泊松随机抽样，可通过R中的帮助功能，很容易学会使用。

2.5 分层随机抽样举例

【例6】试以文献[5]第208-209页“表9-1”的资料作为“抽样框”，并以“sex”为分层因素，实施分层随机抽样。

解答：在R中，实现分层随机抽样的strata( )函数被放置在sampling包中，使用前必须先下载并导入到R软件中。操作的步骤如下：①将安装了R软件的计算机联网并启动R软件；②选择“程序包(Packages)”并选择一个镜像(Set CRAN mirror…)；③选择“安装程序包(Install package(s)…)”；④在弹出的长条形“程序包(packages)”窗口内(约有数千行，其中少部分是“程序包”，绝大多数是“函数”)浏览sampling；⑤在R中使用下面的语句就可实现前述的目的。

在strata( )函数中未明确写出参数method="srswor"，系统默认为“分层(无放回)随机抽样”。

> data1<- read.table("F:/studyr/sex_age.txt",header=T)

> sub1<- strata(data1,stratanames="sex",size=c(4,5),description=TRUE)

第一句表明，从F盘上文件夹为studyr内读取文本文件sex_age.txt赋值给变量(本质上是数据框)data1。

第二句表明，调用strata( )函数，采用默认的随机抽样方法(即分层随机抽样)；设置分层因素为sex；分别从F层与M层抽取4例与5例受试对象或样品；需要对随机抽样出来的样品进行详细描述“description=TRUE”。

Stratum 1

Population total and number of selected units: 12 4

Stratum 2

Population total and number of selected units: 8 5

以上结果表明，从第1层(即F层)12个样品中随机抽取了4个样品；从第2层(即M层)8个样品中随机抽取了5个样品。

Number of strata 2

Total number of selected units 9

以上结果表明，总体中总共有两层，共随机抽取9个样品。

Warning message:

In strata(data1, stratanames = "sex", size = c(4, 5), description = TRUE) :

the method is not specified; by default, the method is srswor

以上结果表明，系统给出了“警告信息”，在调用strata( )函数时，关于抽样方法的参数未指定，作为默认方法，采取的是分层(无放回)随机抽样(srswor)。

> sub1

该语句表明，要求系统呈现出分层随机抽样的结果sub1中的与抽样有关的样品信息。

SexIDunitProbStratum1F10.333333314F40.3333333116F160.3333333119F190.333333317M70.625000028M80.6250000210M100.6250000211M110.6250000218M180.62500002

以上结果表明，第1列为被抽取的样品的编号、第2列为分层因素sex的水平代码、第3列为被抽取的样品在总体中的编号、第4列为各行上的样品被抽取的概率(F层中总共12个样品，抽取4个，每一个被抽取的概率为4/12=1/3=0.333333；M层中总共8个样品，抽取5个，每一个被抽取的概率为5/8=0.625)、第5列为层的编号。

>getdata(data1,sub1)

这一句的目的是调用getdata( )函数，显示被抽取的样本中每个样品的全部信息(即各变量及其取值)。

idagesexIDunitProbStratum1160F10.333333314457F40.33333331161633F160.33333331191949F190.333333317760M70.625000028864M80.62500002101016M100.62500002111158M110.62500002181840M180.62500002

以上结果表明，与前面的输出结果相比较，增加了“年龄(age)”及其取值。如果原数据集(或抽样总体)中除分层因素外，还有50个变量及其取值，此时，都将全部显示出来。

在strata( )函数中明确写出参数method="srswor"，指明要进行分层(无放回)随机抽样。

> data1<- read.table("F:/studyr/sex_age.txt",header=T)

> sub2<- strata(data1,stratanames="sex",size=c(4,5),method="srswor",description=TRUE)

与前面的程序相比较，多了参数method="srswor"。

> sub2

SexIDunitProbStratum4F40.333333316F60.3333333117F170.3333333119F190.333333313M30.625000027M70.625000028M80.6250000211M110.6250000212M120.62500002

以上结果表明，被抽取的样品编号发生了改变。

>getdata(data1,sub2)

idagesexIDunitProbStratum4457F40.333333316631F60.33333331171739F170.33333331191949F190.333333313337M30.625000027760M70.625000028864M80.62500002111158M110.62500002121263M120.62500002

以上结果表明，分层随机抽样的结果发生了变化。

2.6 整群随机抽样举例

2.6.1 数据集介绍

在R软件的MASS包中，有一个名为Insurance的数据集。其内记录了某保险公司1973年第三季度车险投保人的相关信息。其各观测(即行)代表投保人，5列的列名分别为：第1列为District(投保人家庭住址所在区域，代号为1至4)；第2列为Group(所投保汽车的发动机排放量，其各水平分别为：<1升、1.0～1.5升、>1.5～2升、>2升共四个等级)；第3列为Age[投保人的年龄，其各年龄档为：<25岁、25～30岁(不含30岁)、30～35岁、>35岁]；第4列为Holders(投保人数量)；第5列为Claims(要求索赔的投保人数量)。

2.6.2 使用sampling包中的cluster( )函数进行整群随机抽样

> sub3<- cluster(Insurance,clustername="District",size=2,method="srswor",description=TRUE)

以上语句的目的是调用cluster( )函数对Insurance数据集进行整群随机抽样，群的标志为“District”(即区域)、随机抽取的群数为2、将采取简单(无放回)随机抽样(即srswor)方法从4个群中随机地抽取两个群、希望对被抽取的样品信息进行描述(即description=TRUE)。

Number of selected clusters: 2

Population total and number of selected units 64 32

以上结果表明，随机抽取了两个群，共有64个样品，而被抽取的样品数为32个。

> getdata(Insurance,sub3)

以上语句表明，调用getdata( )函数显示从Insurance数据集中抽取的两个群中的全部样品。

GroupAgeHoldersClaimsDistrictIDunitProb1<1L<2519738110.52<1L25～2926435120.551～1.5L<2528463150.561～1.5L25～2953684160.5……18<1L25～29139192180.519<1L30～35151222190.517<1L<2585222170.5261.5～2L25～29175462260.5……

以上是被抽取的32个样品，为节省篇幅，两个群内都只保留了4个样品，其他样品被省略了。由于共有4个群，因此，抽取两个群时，对于每个群而言，被抽中的概率都为0.5。

2.7 bootstrap随机重抽样举例

2.7.1 概述

bootstrap随机重抽样是以原始数据为基础的模拟抽样统计推断法，其基本思想是：在原始数据范围(假定总样本含量为n)内做有放回的再抽样，每次抽取的样本含量都是m，原始数据中每个观测(样品或个体)每次被抽中的概率相等，即1/n，所抽得的样本被称为bootstrap样本。

bootstrap样本有何用途呢？当人们无法驾驭总体但可以反复获得bootstrap样本时，由它们所呈现的规律就非常接近无法驾驭的那个总体。下面用一个可以驾驭的总体为例，先呈现出总体中一个定量变量的取值的频数分布情况，再采取有放回的随机抽样，获得一个样本含量较大(如1000或10000)的bootstrap样本，再呈现该bootstrap样本的频数分布。比较这两个频数分布的形状是否接近。

2.7.2 用于抽取bootstrap样本的数据集

在R中，有一个内置的faithful数据集(Old Faithful Geyser Data)，它记录了美国怀俄明州黄石国家公园内的古老而又忠实的喷泉的喷射持续时间eruptions(min)和等待时间waiting(min)(即相邻两次喷射之间的时间间隔)。

> faithful

此语句用于显示faithful数据集中的全部数据(n=272)。

eruptionswaiting13.6007921.8005433.33374……2704.417902711.817462724.46774……

以上显示出faithful数据集中的开始和结尾的各3个观测结果。

2.7.3 显示总体中eruptions变量的频数分布

> attach(faithful)

> hist(eruptions,breaks=25)

第一句的目的是绑定数据；第二句的目的是绘制eruptions变量的频数直方图，因篇幅所限，图形从略。

2.7.4 从总体中进行2000次有放回的随机抽样，获得样本含量n=2000的bootstrap样本

> boot.sample<- sample(eruptions,2000,rep=T)

以上语句的目的就是为了实现从总体中进行2000次有放回的随机抽样，获得样本含量n=2000的bootstrap样本。

2.7.5 将总体与bootstrap样本中的eruptions变量的频数分布直方图平行地绘制出来

> par(mfrow=c(1,2))

> hist(eruptions,breaks=25)

> hist(boot.sample,breaks=25)

> par(mfrow=c(1,1))

以上四个语句的目的分别为：

第一句：设置作图窗口为一行两列(就是希望把两幅图左右放置)。

第二句：在左边放置总体中的eruptions变量的频数分布直方图。

第三句：在右边放置bootstrap样本中的eruptions变量的频数分布直方图。

第四句：设置作图窗口为一行一列(就是把前面的一行上绘制两幅图的设置改回默认状态，即一行上只绘制一幅图)。

由图形绘制的结果(因篇幅所限，此处从略)可以清楚地看出：bootstrap样本呈现的图形几乎与总体一模一样。若总体真是不可驾驭的，那就可以通过bootstrap样本呈现的形状去推断它。

[1] 黄文, 王正林. 数据挖掘: R语言实战[M]. 北京: 电子工业出版社, 2015: 34-39.

[2] 李诗羽, 张飞, 王正林. 数据分析: R语言实战[M]. 北京: 电子工业出版社, 2015: 88-156.

[3] 方匡南, 朱建平, 姜叶飞. R数据分析: 方法与案例详解[M]. 北京: 电子工业出版社, 2015: 54-168.

[4] Joseph Adler. R语言核心技术手册[M]. 2版. 刘思喆, 李舰, 陈钢, 等译. 北京: 电子工业出版社, 2015: 417-421.

[5] 胡良平. 科研设计与统计分析[M]. 北京: 军事医学科学出版社, 2012:129-274.

(本文编辑：陈 霞)

The realization of the random sampling and its application based on R software

ZhangXiaojia1,HuLiangping1,2*

(1.ConsultingCenterofBiomedicalStatistics,AcademyofMilitaryMedicalSciences,Beijing100850,China; 2.SpecialtyCommitteeofClinicalScientificResearchStatisticsofWorldFederationofChineseMedicineSocieties,Beijing100029,China

*Correspondingauthor:HuLiangping,E-mail:lphu812@sina.com)

The paper aims to make it convenient for readers to utilize R software to generate random number from various distributions and implement varieties of random sampling methods. The paper introduced the conception and corresponding functions of random number generators. We presented cases of generating random number from both normal distribution and uniform distribution. Consequently, readers may easily generate random number by R software. The paper also introduced the conception and realization of random sampling both with and without replacement, systematic random sampling, stratified random sampling, cluster random sampling and bootstrap random sampling. Therefore, readers may use R software to realize varieties of random sampling methods. The fact indicated that R software may be simply obtained and utilized. R software may be used to solve random sampling problem in experimental designs conveniently, due to its powerful function and wide application.

R software; Random number generator; Normal distribution; Uniform distribution; Random sampling; Bootstrap random sampling

*通信作者：胡良平，E-mail：lphu812@sina.com)

R195.1

A

10.11886/j.issn.1007-3256.2016.06.002

国家高技术研究发展计划课题资助(2015AA020102)

2016-12-03)