基于IDA方法的高速铁路连续梁桥易损性分析
2016-02-24向宝山崔圣爱
韩 兴,李 鑫,向宝山,崔圣爱,祝 兵
(西南交通大学 土木工程学院,四川 成都 610031)

基于IDA方法的高速铁路连续梁桥易损性分析
韩兴,李鑫,向宝山,崔圣爱,祝兵
(西南交通大学土木工程学院,四川成都610031)
摘要:大量经验表明高速铁路预应力混凝土桥在地震下的破坏主要体现在桥墩和支座位置。为了得到该种桥型地震下的易损性曲线,利用典型高速铁路连续梁桥为计算实例,采用IDA方法(增量动力分析法),通过有限元软件OpenSees建立了地震易损性分析模型。根据场地类型,选取20条地震波进行非线性时程分析,通过调幅得到200个计算工况。定义4种破坏极限状态,并通过回归分析建立不同破坏极限状态地震需求和地震动强度指标关系。基于对数正态分布假设绘制各个破坏状态对应的易损性曲线,并通过一阶可靠度理论得到整体易损性曲线。
0引言
目前,中国的高速铁路建设方兴未艾。连续梁桥以其刚度大、变形小、动力特性好、主梁变形挠曲线平缓等优点广泛运用于高速铁路中[1]。事实表明,桥梁结构作为交通线路的重要枢纽,而在地震灾害发生时是易损害的[2]。近年,我国相继发生了汶川地震、玉树地震等地震灾害,造成了大量桥梁破坏,引发了大量社会和经济问题。这便使桥梁结构地震风险性分析显得愈发重要。
地震风险性分析主要包括3个方面:(1)地震危险性分析;(2)地震易损性分析;(3)地震灾害损失评估[3]。其中,地震易损性分析用来评价结构在不同强度地震作用下,发生某一规定破坏状态的超越概率。因此,易损性分析能合理地评价桥梁的抗震性能[4]。易损性表示在某一强度的地震作用下结构的破坏超过某一规定值的概率。易损性曲线是目前国际上主要用来评价结构易损性的方式,对于桥梁的易损性可以通过以下函数表达:
Fragility=P[EDP≥LS|IM],
式中,EDP工程需求参数;LS为结构破坏状态;IM地震动强度。
现今,国内对桥梁结构的易损性分析虽处于起步阶段,仍取得了一定的研究成果[5-7]。桥梁结构作为一个系统,地震作用下的整体破坏概率大于单一构件的破坏概率。目前,国内对于桥梁结构整体易损性的研究也相对较少。
高速铁路线路中桥梁数量庞大,其中相当数量为连续梁桥。地震作用下连续梁桥的震害主要体现在支座破坏和桥墩破坏上。具体表现为支座发生过大位移导致失稳、主梁滑脱和落梁;墩底曲率过大导致钢筋屈服和混凝土压溃,进而导致桥墩破坏。对高速铁路连续梁桥进行易损性分析,可评定其抗震性能、预测其地震风险,为高速铁路桥梁抗震设计提供参考。
本文以某高速铁路连续梁桥为例,给出基于IDA方法的高速铁路连续梁桥地震易损分析的一般方法。基于位移准则给出支座的损伤指标,基于墩底曲率给出桥墩的损伤指标。利用OpenSees建立了有限元分析模型,进行非线性时程分析,通过对数正态分布假设得到支座和桥墩的易损性曲线;进而,通过一阶可靠度理论得到结构的整体易损性曲线。
1有限元模型的建立
1.1桥梁工程概况
本文研究对象为某高速铁路连续梁桥,桥跨径布置为(32+48+32) m,如图1所示。主梁采用单箱单室箱形截面,中支点梁高为3.4 m,边支点及跨中梁高为2.8 m。全桥箱梁底板箱宽4.5 m,顶板宽7.0 m,腹板厚为0.4~0.6 m,顶板厚0.3 m。桥墩为圆端形截面。箱梁采用C50高性能混凝土,桥墩采用C35混凝土,承台采用C40混凝土。桥墩纵筋为HRB400,桩身受力钢筋及桥墩箍筋为HPB300。
本桥支座采用铁路连续梁球形支座,容许位移为150 mm。场地条件为I类,地震动反应谱特征周期为0.35 s。
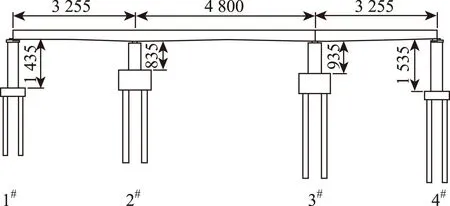
图1 桥跨布置图(单位:cm)Fig.1 Arrangement of bridge spans(unit:cm)
1.2有限元模型
本文利用OpenSees建立了桥梁结构有限元动力分析模型。由于桥址处地质条件良好,分析过程中不考虑桩土作用,即将墩底固结。
建模时,主梁、桥墩和支座分别采用3种不同的单元。出于能力保护原则,地震作用下桥墩首先进入塑性状态而保证主梁的安全。因此,认为地震作用下主梁处于线弹性状态,故采用弹性梁柱单元模拟主梁;考虑桥墩的非线性因素,采用非线性梁柱单元模拟桥墩。本文采用零长度单元模拟支座,通过定义非线性支座材料来模拟支座的弹塑性。
建模时,对钢筋、混凝土和支座分别定义3种不同的材料本构。对于钢筋,本文采用简化的理想弹塑性模型,采用OpenSees中的钢筋材料Steel01对其进行模拟。约束混凝土的本构关系采用了过镇海模型,采用OpenSees中的混凝土材料Concrete01对其进行模拟。为了较准确地模拟支座的抗震性能,采用了程序中的理想弹塑性单元来模拟支座材料的力与变形之间的关系,即零长度单元的材料特性。
全桥有限元模型如图2所示。
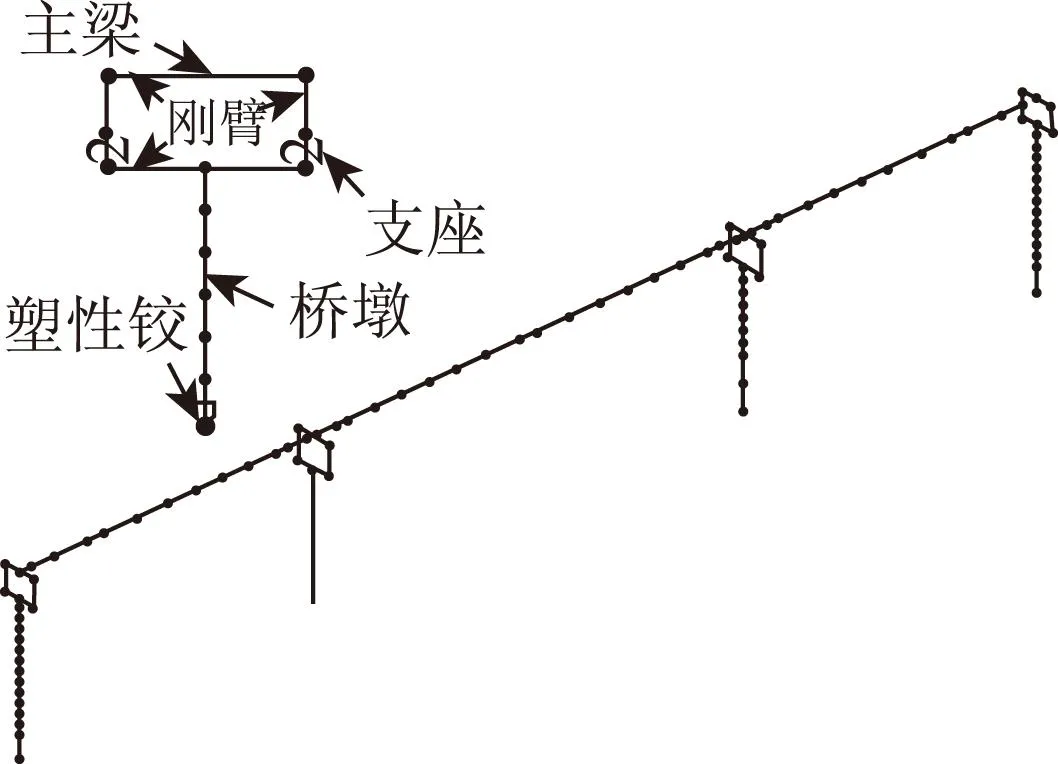
图2 全桥有限元模型Fig.2 Finite element model of bridge
2地震波选取
本文采用了增量动力分析(IDA)方法,IDA方法实质上是一种参数分析法,主要包含两种参数:结构性能参数和地震动强度参数。地震动特性对于结构在地震下的响应起着重要的作用,不同的地震幅值、频谱特性和持时与结构本身的动力性能一起影响着结构地震中的受力、变形。在IDA方法中,由于强度峰值在分析中可以不断进行调整,因此选择地震波时主要考虑频谱特性、持续时间和地震波数量。选取地震波的原则如下:
(1)应尽量使所选择的地面运动记录的卓越周期、震中距与拟建场地一致;
(2)考虑地震需求的随机性,应尽量具有全面性,一般地震的持续时间取结构基本周期的5~10倍为宜;
(3)在运用IDA方法对结构进行抗震性能评估时,选取10~20条地震波能达到一定的精度[8]。
按照以上原则,根据桥址处地质条件从PEER数据库中选取了20条天然地震波,选用地面峰值加速度(PGA)作为地震动强度参数,每列地震波经过10次调幅,峰值加速度从0.1g~1.0g,增幅为0.1g。
3破坏状态和回归分析
3.1破坏状态定义
在大多数桥梁地震易损性分析中,墩柱延性被作为主要的指标参数来衡量结构的破坏状态。Shinozuka等人对同一类型的桥梁墩柱进行了大量分析,归纳出了4种破坏状态:轻微破坏、中等破坏、严重破坏和结构倒塌[9]。
根据实际情况,本文从两个方面定义桥梁结构的破坏状态,即桥墩的破坏和支座的破坏。
3.1.1桥墩破坏状态定义
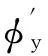
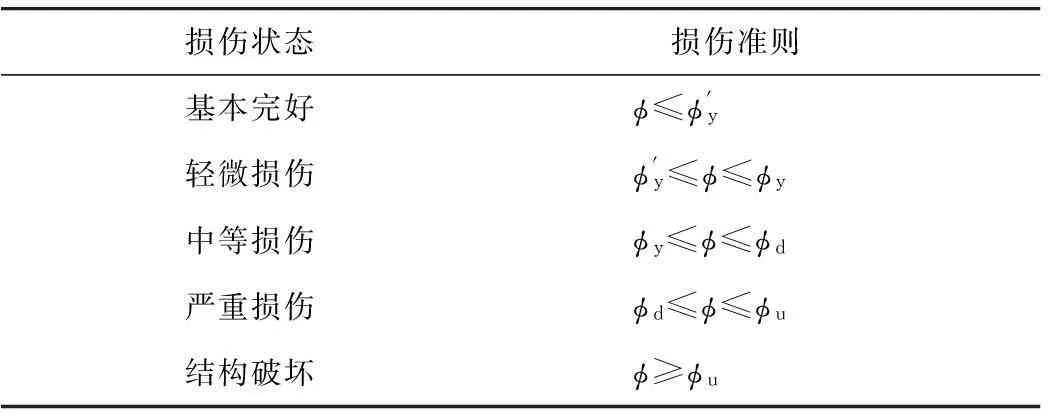
表1 桥墩破坏状态定义
3.1.2支座破坏状态定义
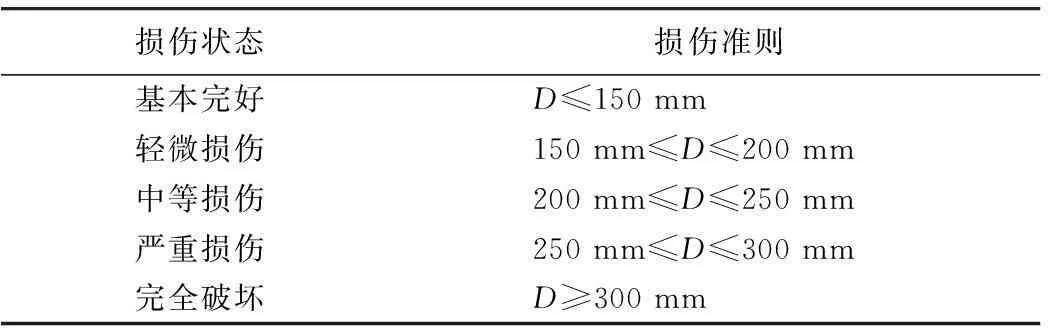
表2 支座破坏状态定义
3.2回归分析
对于每个工况,提取墩底曲率、墩顶位移等计算结果。将相同PGA的工况结果分为一组,对同组20个工况的最大响应取平均值得到该级地震下的平均最大响应。
将结构地震需求和对应的PGA取对数,便可在坐标内得到10个散点。再对这些散点进行回归分析,便可以得到结构地震需求与PGA的关系方程式。
lnu=AlnPGA+B ,
(1)
式中,u为结构地震需求;A和B为回归方程系数。
通过求同组20个工况的最大响应的对数标准差,便可建立响应对数标准差与PGA的关系方程式。
(2)
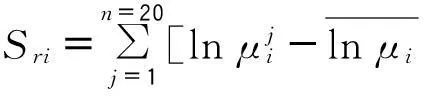
经过多次拟合,最终决定对于墩底曲率和支座两种损伤指标的标准差分别采用式(3)和式(4)进行拟合。
基金羊群行为与投资组合崩盘风险——基于序贯交易模型的实证研究..................................................................................................................................池国华 张向丽(30)
(3)
(4)
3.2.1桥墩需求回归分析
对固定墩底曲率各个PGA下的结构地震需求平均值取对数及对数标准差,结果见表3。

表3 桥墩曲率回归分析数据
通过回归分析,桥墩墩底曲率需求均值对数与峰值加速度PGA之间的函数关系如下:
lnφd=2.186 4lnPGA-8.324 5。
(5)
桥墩墩底需求对数标准差与峰值加速度PGA之间的函数关系式如下:
βφ=-0.000 32(PGA)3-0.003 80PGA2+
0.120 67PGA+0.326 67。
(6)
墩底需求回归分析和墩底需求标准差回归分析分别如图3、图4所示。
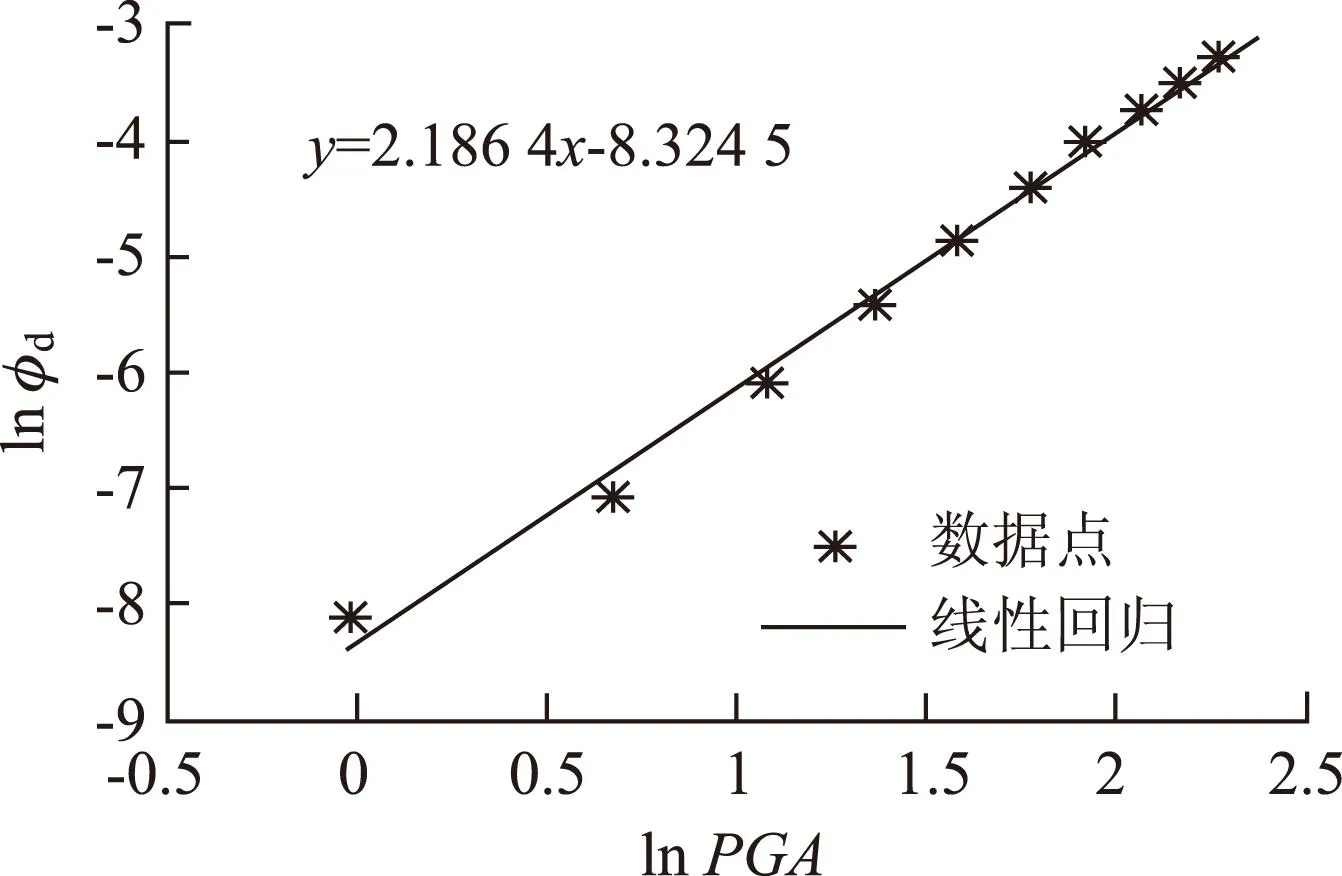
图3 桥墩墩底需求回归分析Fig.3 Regression analysis of pier bottom demand
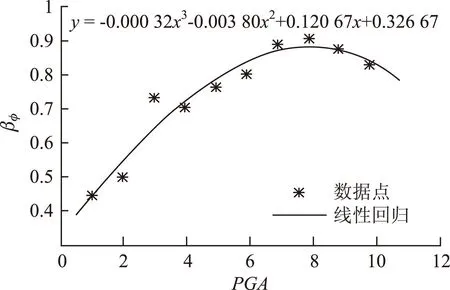
图4 桥墩墩底需求标准差回归分析Fig.4 Regression analysis of pier bottom demand standard deviation
3.2.2支座需求回归分析
对4号墩支座位移各个PGA下的结构地震需求平均值取对数及对数标准差,结果见表4。

表4 4号墩纵向地震位移回归分析数据
通过回归分析,桥墩支座位移需求均值对数与峰值加速度PGA之间的函数关系式如下:
lnDd=1.422 1lnPGA-4.417 8。
(7)
根据回归分析所得样本标准差的分布特点,对于支座位移标准差的拟合采用了三次多项式,位移对数标准差与PGA之间的函数关系式如下:
βd=-0.000 53(PGA)3+0.009 45(PGA)2-
0.038 97(PGA)+0.436 18 。
(8)
支座需求回归分析和支座需求标准差回归分析分别如图5、图6所示。
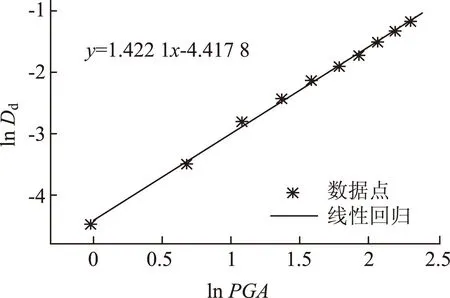
图5 活动支座需求回归分析Fig.5 Regression analysis of movable bearing demand
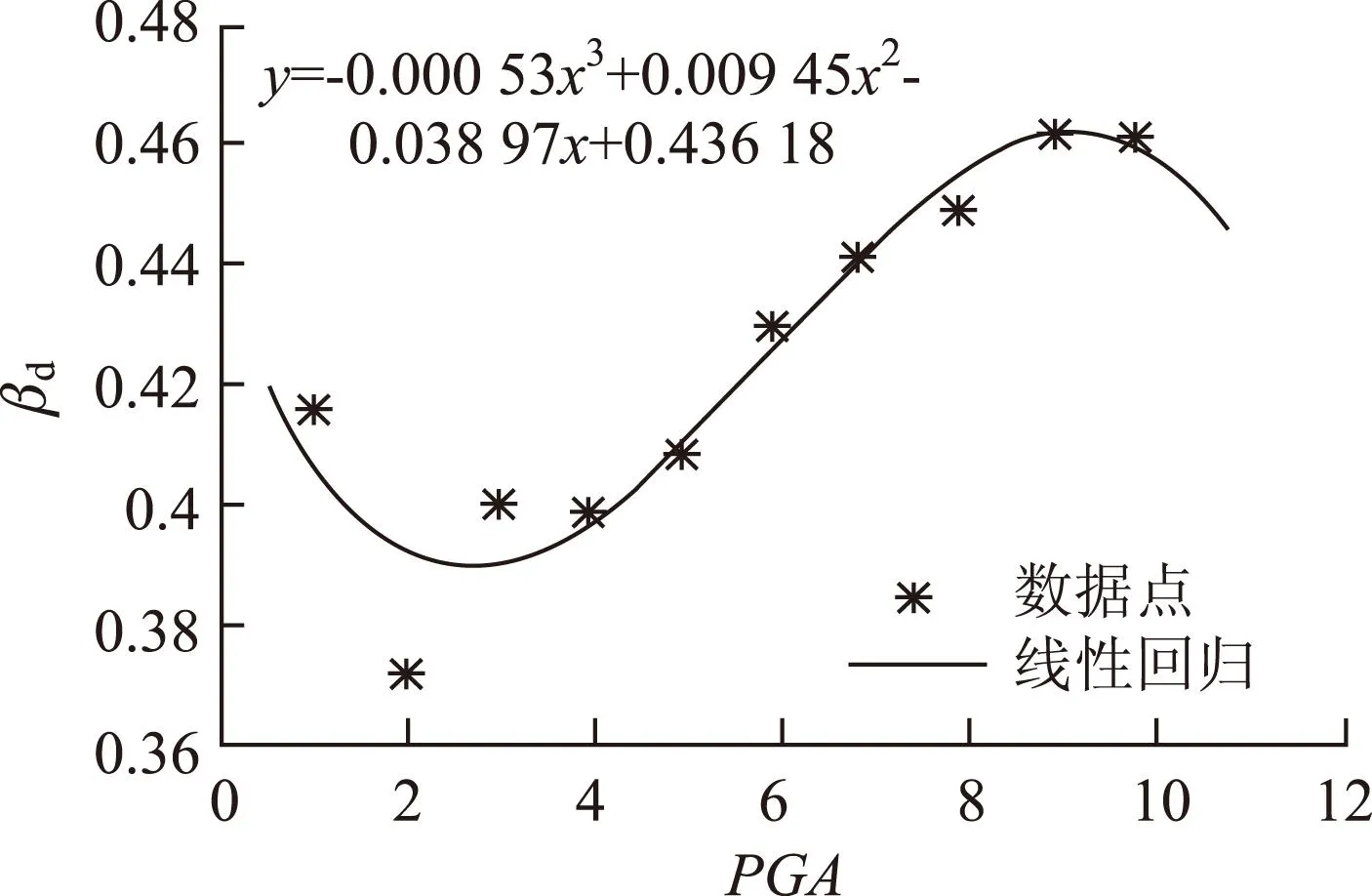
图6 活动支座需求的标准差回归分析Fig.6 Regression analysis of movable bearing demand standard deviation
4易损性曲线绘制
4.1构件易损性
易损性曲线描述了结构在不同水平的地震作用下,达到某一破坏状态的概率,在特定阶段的失效概率pf可由式(9)确定:
(9)
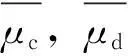
桥墩和支座的易损性曲线分别如图7、图8所示。
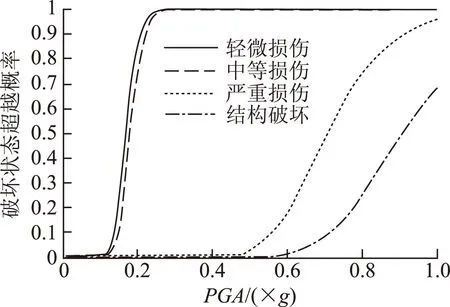
图7 桥墩易损性曲线Fig.7 Vulnerability curves of pier
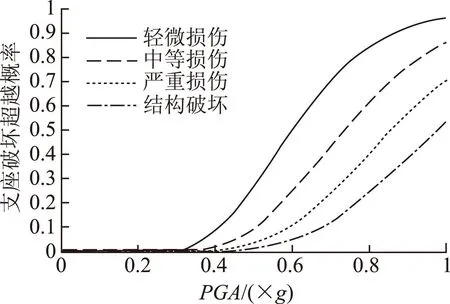
图8 支座易损性曲线Fig.8 Vulnerability curves of bearing
从图7中可以发现,对于桥墩来说结构的轻微损伤和中等损伤的易损性曲线在加速度值较小时基本重合,在地震加速度0.17g到0.23g左右发生轻微损伤和中等损伤的概率激增,0.23g以后桥墩基本都会发生轻微损伤和中等损伤。桥墩在PGA从0.42g以后发生严重损伤,而桥墩结构只有在PGA为0.6g左右的时候才会开始有破坏的概率。
图8中我们可以发现,对于支座来说,随着PGA的增大,其发生不同破坏的概率曲线呈递进的分布,结构发生各种损伤破坏的概率总是有着轻微损伤>中等损伤>严重损伤>结构破坏概率的规律。
4.2整体易损性
对于结构整体而言,桥墩的倒塌以及支座的破坏都可能造成整个桥梁结构的失效。因此,需要综合考虑各个构件的易损性从而得到整体结构的易损性曲线[11]。以下将基于可靠度理论对整体结构的失效概率进行评价。
在进行整体易损性分析的过程采用一阶可靠度理论来估计结构的失效概率,对于桥梁来说我们认定该结构的可靠度体系属于串联体系[12],该体系下的桥梁构件破坏处在一个相对独立的状态下。如式(10)所示,我们认为一旦结构有部件发生破坏则整体发生破坏。
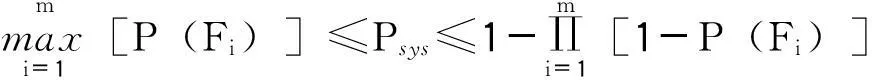
(10)
由此可以绘制结构整体易损性曲线,见图9~图12。
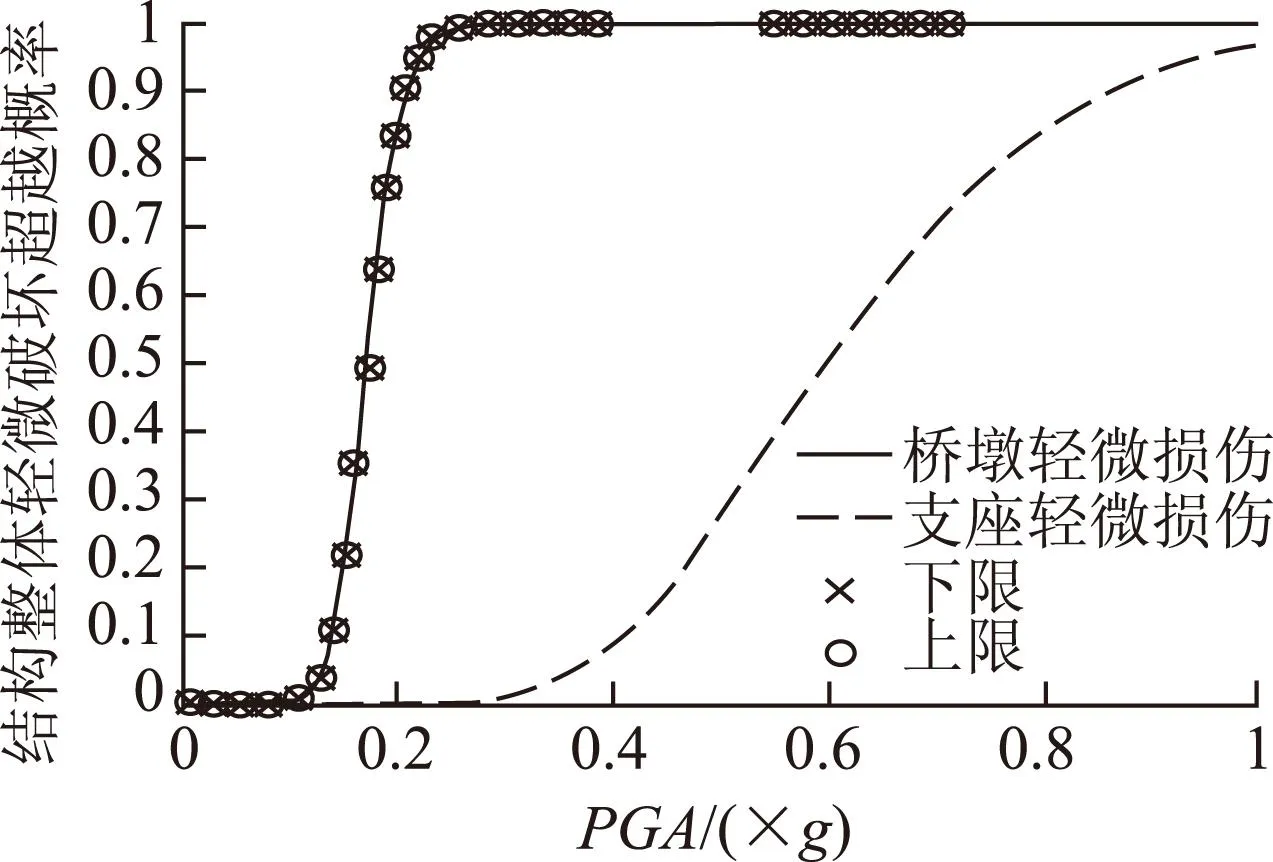
图9 整体轻微损伤易损性曲线Fig.9 Vulnerability curves of slight damage
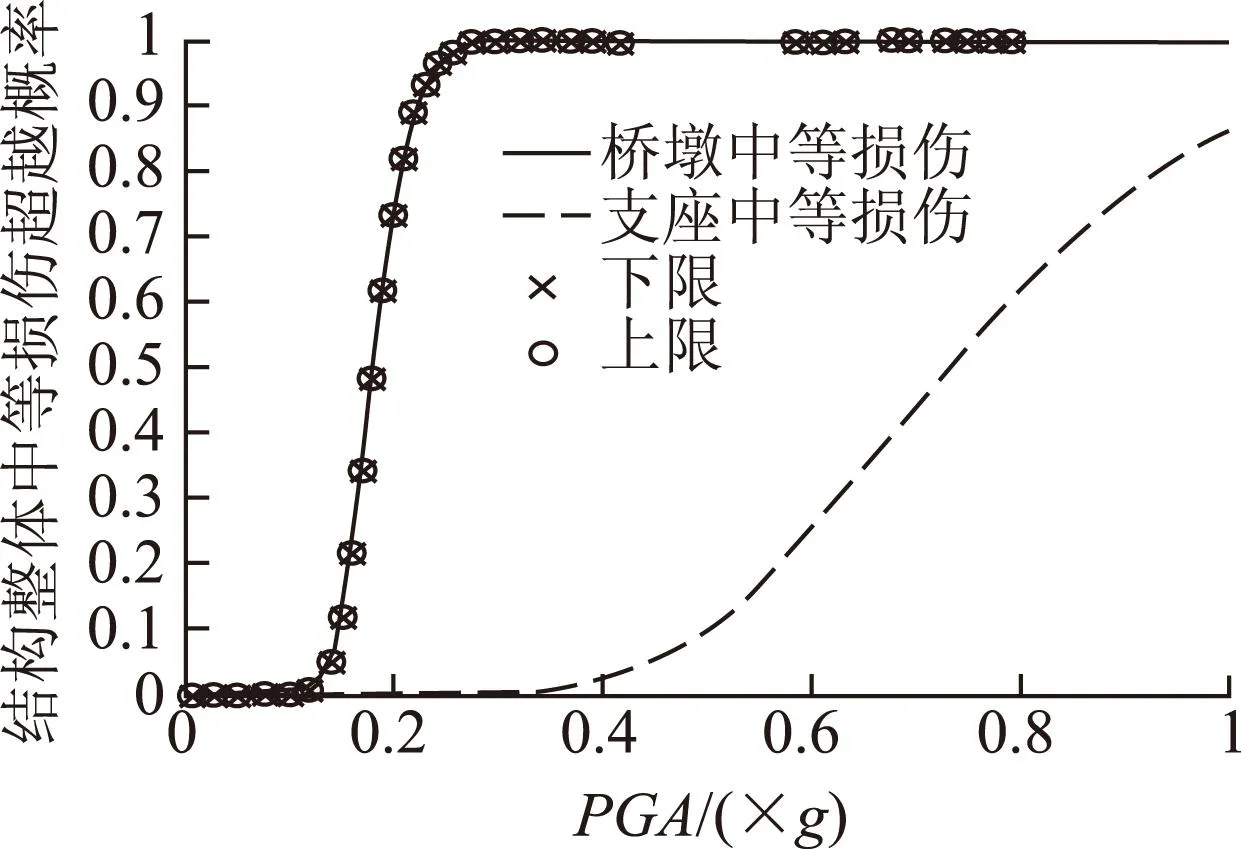
图10 整体中等损伤易损性曲线Fig.10 Vulnerability curves of integral medium damage
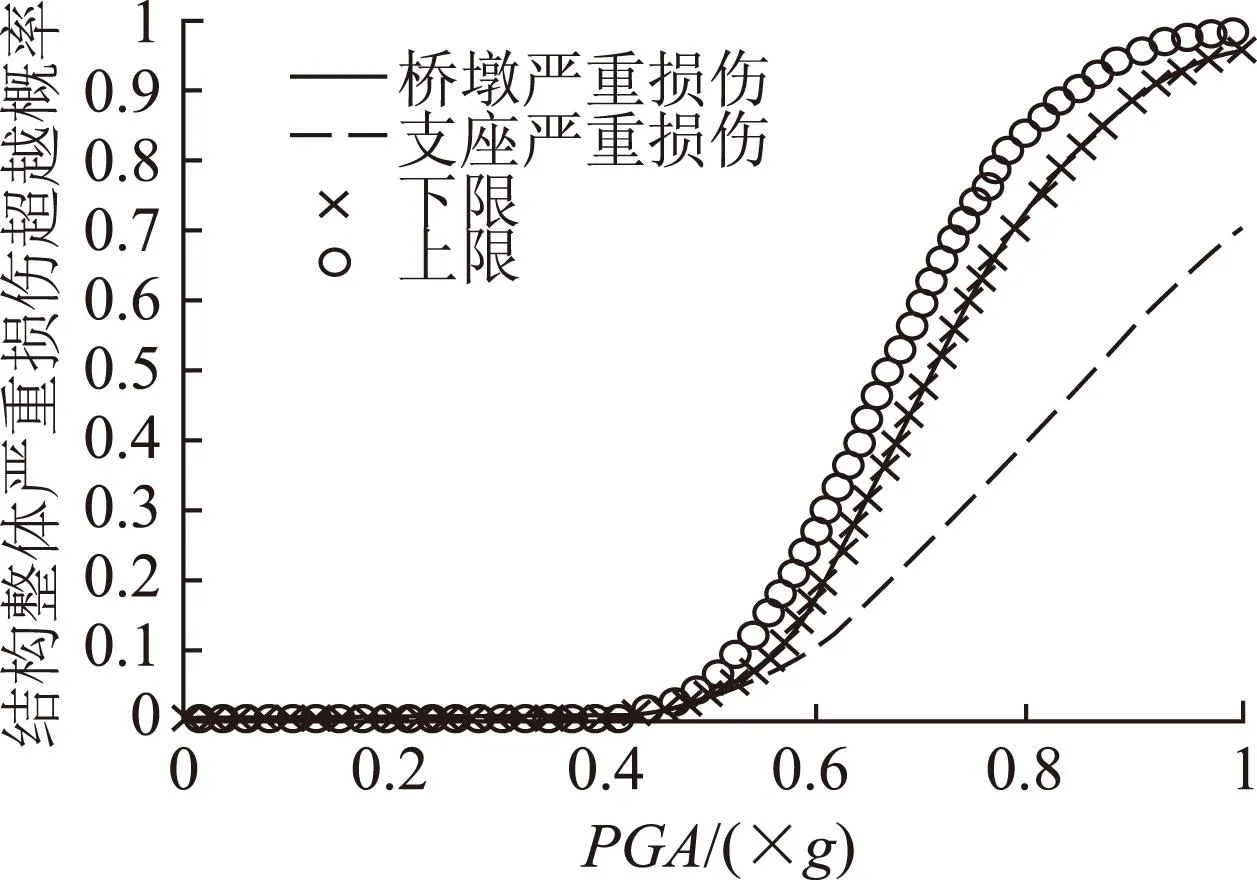
图11 整体严重损伤易损性曲线Fig.11 Vulnerability curves of integral severe damage
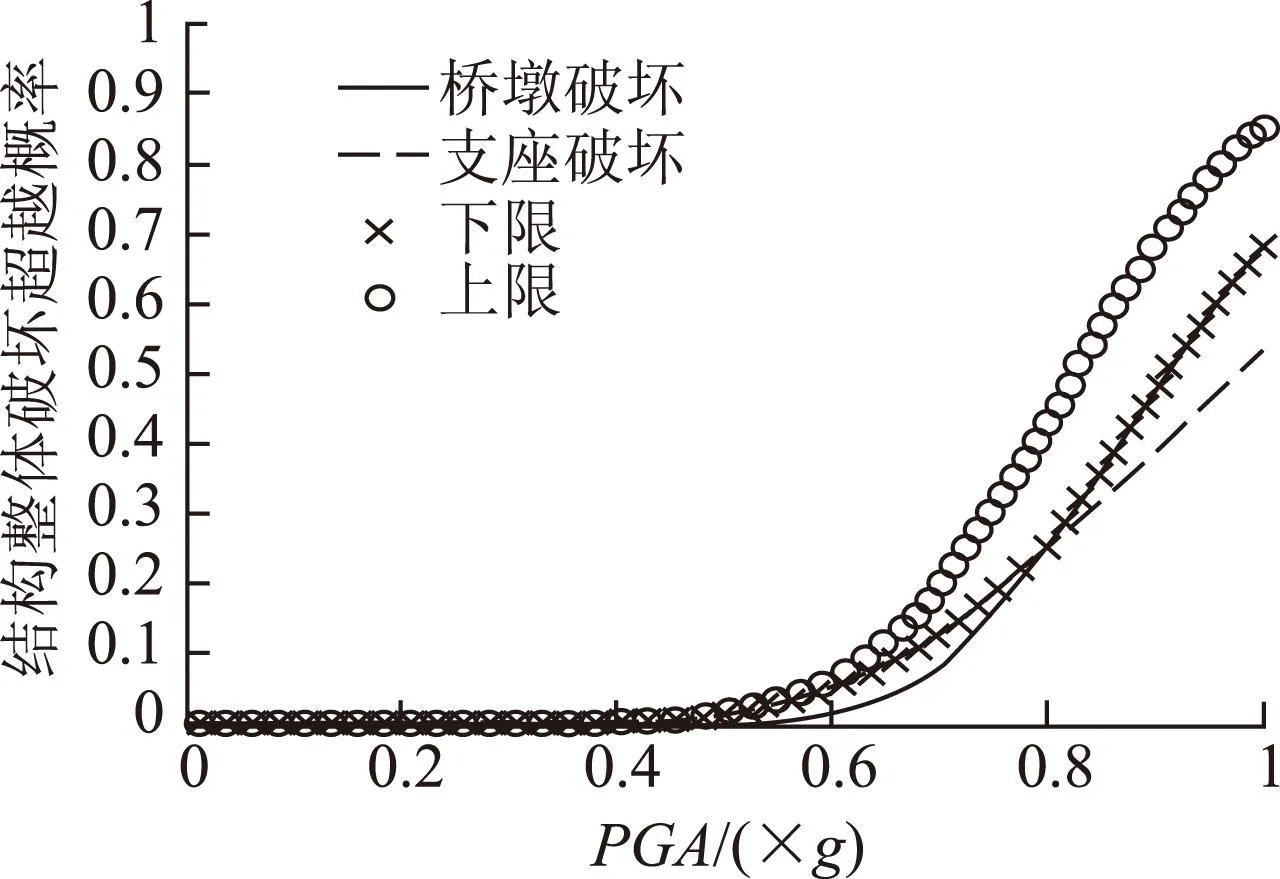
图12 整体破坏损伤易损性曲线Fig.12 Vulnerability curves of integral destructive damage
从图11和图12可以看出,将桥梁看成一个体系,桥梁体系发生轻微与中等损伤时整体破坏的概率是由桥墩的破坏概率控制,而桥梁体系发生严重和整体破坏的概率则基本是有支座的破坏概率所控制。
5结论
本文通过IDA的方法和OpenSees软件对高速铁路连续梁桥进行了地震易损性分析;通过对构件的破坏状态定义和回归分析绘制了桥墩和支座的易损性曲线。结合一阶可靠度理论和地震易损性分析相结合提出了高速铁路连续梁桥整体的易损性曲线。本文得到以下结论:
(1)现阶段对于高速铁路连续梁桥的地震易损性分析研究,对高速铁路桥梁这种特殊的桥梁形式在地震下的风险分析有着重要意义,同时对于桥梁结构的抗震性能研究,震后维修策略都有着重要的应用价值。
(2)通过OpenSees有限元建模,通过后期数值软件的数据处理,可以大大提高桥梁易损性的计算效率和准确度。
(3)通过对结构构件和整体的易损性曲线分析,可以发现高速铁路连续梁桥梁体系发生轻微与中等损伤时整体破坏的概率是由桥墩的破坏概率控制,而桥梁体系发生严重和整体破坏的概率则基本是由支座的破坏概率所控制。
(4)本文的易损性曲线分析是针对高速铁路连续梁这种单一的桥型,所得到的结果有一定的共性,可以在今后高速铁路连续梁桥抗震设计中起到一定的参考价值,论文所提出的易损性的计算模式对于任何桥梁都可以采用,有一定的科研设计应用价值。
参考文献:
References:
[1]康欣. 高速铁路连续梁桥地震响应分析[D]. 长沙:中南大学, 2013.
KANG Xin. Seismic Response Analysis of High-speed Continuous Girder Bridges[D]. Changsha: Central South University,2013.
[2]WANG H H,刘晶波. 地震作用下钢筋混凝土桥梁结构易损性分析[J]. 土木工程学报, 2004,36(7): 47-51.
WANG H H, LIU Jin-bo. Seismic Fragility Analysis of Reinforced Concrete Bridges[J]. China Civil Engineering Journal, 2004, 36 (7) : 47-51.
[3]吕大刚, 李晓鹏, 王光远. 基于可靠度和性能的结构整体地震易损性分析[J]. 自然灾害学报, 2006, 15(2):107-114.
LÜ Da-gang, LI Xiao-peng, WANG Guang-yuan. Global Seismic Fragility Analysis of Structures Based on Reliability and Performance[J]. Journal of Natural Disasters, 2006, 15 (2):107-114.
[4]刘震. 中承式钢管混凝土拱桥地震易损性分析[J]. 公路交通科技, 2015, 32(8):70-79.
LIU Zhen. Analysis on Seismic Fragility of Half-through CFST Arch Bridge[J]. Journal of Highway and Transportation Research and Development, 2015, 32(8):70-79.
[5]陈力波, 郑凯峰,庄卫林,等. 汶川地震桥梁易损性分析[J]. 西南交通大学学报, 2012, 47(4): 558-566.
CHEN Li-bo, ZHENG Kai-feng, ZHUANG Wei-lin, et al. Analytical Investigation of Bridge Seismic Vulnerability in Wenchuan Earthquak [J]. Journal of Southwest Jiaotong University,2012, 47 (4): 558-566.
[6]郑凯锋, 陈力波, 庄卫林,等. 基于概率性地震需求模型的桥梁易损性分析[J]. 工程力学,2013,30(5): 165-171,187.
ZHENG Kai-feng, CHEN Li-bo, ZHUANG Wei-lin, et al. Bridge Vulnerability Analysis Based on Probabilistic Seismic Demand Models [J]. Engineering Mechanics, 2013,30(5): 165-171,187.
[7]李立峰, 吴文朋, 黄佳梅, 等. 地震作用下中等跨径RC连续梁桥系统易损性研究 [J]. 土木工程学报, 2012,45(10):152-160.
LI Li-feng, WU Wen-peng, HUANG Jia-mei, et al. Study on System Vulnerability of Medium Span Reinforced Concrete Continuous Girder Bridge under Earthquake Excitation[J]. China Civil Engineering Journal, 2012, 45 (10): 152-160.
[8]LUCO N, CORNELL C A. Effects of Connection Fractures on SMRF Seismic Drift Demands[J]. Journal of Structural Engineering 2000, 126(1):127-136.
[9]SHINOZUKA M, FENG M Q, LEE J, NAGANUMA T. Statistical Analysis of Fragility Curves[J]. Journal of Engineering Mechanics,2000,126(12):1224-1231.
[10]李立峰, 吴文朋, 黄佳梅, 等. 地震作用下中等跨径RC连续梁桥系统易损性研究[J]. 土木工程学报,2012,45(10):152-160.
LI Li-feng, WU Wen-peng, HUANG Jia-mei, et al. Study on System Vulnerability of Medium Span Reinforced Concrete Continuous Girder Bridge under Earthquake Excitation[J]. China Civil Engineering Journal,2012,45(10):152-160.
[11]陈力波,郑凯峰,栗怀广,等.基于扩展动量分析的桥梁地震易损性研究[J]. 公路交通科技. 2012, 29(9): 43-49.
CHEN Li-bo, ZHENG Kai-feng, LI Huai-guang, et al. Research of Bridge Seismic Vulnerability Based on Extended Incremental Dynamic Analysis[J]. Journal of Highway and Transportation Research and Development, 2012, 29(9): 43-49.
[12]葛胜锦, 熊治华, 翟敏刚, 等.中小跨径混凝土连续梁桥地震易损性研究[J].公路交通科技,2013, 30(7): 60-65.
GE Sheng-jin,XIONG Zhi-hua,ZHAI Min-gang, et al. Research on Seismic Fragility of Medium and Small Sized Concrete Continuous Girder Bridge[J]. Journal of Highway and Transportation Research and Development, 2013, 30(7): 60-65.
关键词:梁桥工程;高速铁路连续梁桥;IDA方法;地震易损性分析;OpenSees
Analysis of Seismic Fragility of High Speed Railway Continuous Beam Bridge Based on IDA MethodHAN Xing, LI Xin, XIANG Bao-shan, CUI Sheng-ai, ZHU Bing
(School of Civil Engineering, Southwest Jiaotong University, Chengdu Sichuan 610031, China)
Abstract:Many experiences show that high speed railway presstressed concrete bridge’s damage under earthquake mainly reflects in piers and supports. In order to get the fragility curves of this kind of bridge, taking a typical high speed railway continuous beam bridge for example, the seismic fragility analysis model is built by using IDA method and OpenSees FE software. According to the site type, 20 seismic waves are selected for nonlinear time history analysis, and 200 calculating conditions are obtained by amplitude modulation. Four failure limit states are defined, and the relations of seismic demand of different damage limit states with seismic intensity indexes are found by the regression analysis. The corresponding fragility curves of different damage state are drawn based on the assumption of logarithmic normal distribution, and the overall fragility curve is obtained by the first-order reliability theory.
Key words:bridge engineering; seismic fragility analysis; increment dynamic analysis (IDA) method; high speed railway continuous beam bridge; OpenSees
文献标识码:A
文章编号:1002-0268(2016)02-0054-06
中图分类号:U441.3
doi:10.3969/j.issn.1002-0268.2016.02.009
作者简介:韩兴(1985-),男,安徽合肥人,博士研究生.(hanxing1122@163.com)
基金项目:高速铁路运营混凝土连续桥梁地震风险项目(2013G002-A-2)
收稿日期:2015-01-04
