太原市春季PM10浓度波动的分形维数特征及MF－DFA分析

金艳玲

（山西大学商务学院基础部,山西太原030031）

太原市春季PM10浓度波动的分形维数特征及MF－DFA分析

金艳玲

（山西大学商务学院基础部,山西太原030031）

以太原市2016年3月1日至5月31日日均PM10浓度为基础数据,利用分形几何中的计盒维数指标定量刻画浓度变化特征；同时,利用多重分形消除趋势波动分析方法对PM10浓度变化的多重分形特征进行检验,发现太原市春季PM10浓度变化的多重分形特征不明显.

分形；计盒维数；多重分形消除趋势波动分析方法；PM10浓度

灰霾问题是我国环境治理的首要问题.形成灰霾的主要原因之一,便是大气中悬浮的可吸入颗粒物（PM10）.目前,从质量浓度、数量浓度、物相组成、粒度等方面对颗粒物的研究比很多［1］.研究表明,城市空气污染演变过程具有典型的非线性特征,如标度不变性、自相似性及长期持续性等.这些特征使得分形理论在环境科学领域得到了广泛的应用.

分形理论是非线性科学研究中十分活跃的一个分支.它的研究对象是自然界和非线性系统中的不光滑和不规则的几何形体.近年来,利用分形理论讨论城市空气污染的文章较多.文献［2,3］分别讨论了上海与北京空气中可吸入颗粒物粒度分布的分形维数特征,文献［4］讨论了成都在一次雾霾期间PM10浓度波动的分形特征.本文以太原市春季PM10浓度数据为例,利用分形几何中的分形维数指标定量刻画PM10浓度数据的时间变化特征,并利用MF－DFA方法讨论该过程的多重分形特征.

1 数据来源与处理

本文选取2016年3月1日至5月31日,太原市PM10浓度的日平均值为研究对象.数据来源与太原市环境监测城市空气质量实时发布平台,所得数据见图1.

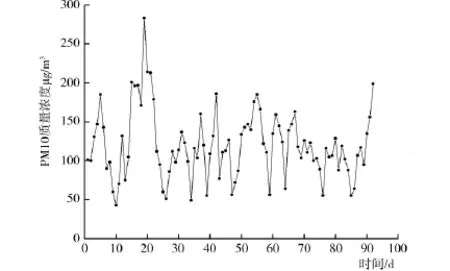
图1 太原市PM10日平均质量浓度时间变化序列

由上图可见,PM10浓度变化具有非周期性、非线性性、非平稳的特点.

2 研究方法与结论

2.1 计盒维数法

设A为Rn空间的任意非空有界子集,对任意一个r＞0,Nr（A）表示用来覆盖A所需边长为r的n维立方体（盒子）的最小数目.则A的盒维数定义为

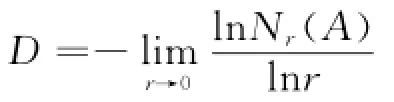
对于所获得的PM10的浓度变化数据,欲计算其盒维数.

首先,用Th作为阀值,将PM10的浓度时间序列转化为时间轴上分布的点集.

其次,用一系列时间尺度r,将点集划分为许多不重复的小区间段（盒子）,并统计覆盖点集所需要的最少盒子数N（r）.

最后,将以上r－N（r）值描绘在双对数坐标轴上,用最小二乘法拟合得到直线斜率,次斜率即为盒维数D.

2.2 MF－DFA方法多重分形消除趋势波动分析方法是检验非平稳时间序列是否具有多重分析特征的方法MF－DFA方法如下：

1）对非平稳时间序列｛xi｝,（i＝1,2,…,N）,其中,N＝92作累计离差

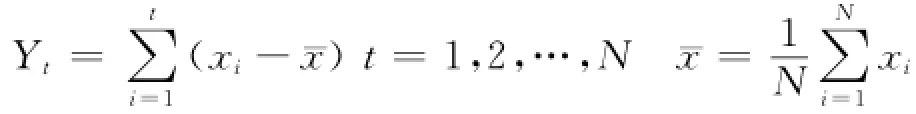
2）用任意r＞0,将序列长度N自首向尾划分为Nr个等长区间,其中为了不舍弃剩余部分,再自尾向首重复以上过程,共得到2Nr个长为r的区间,其上的序列为

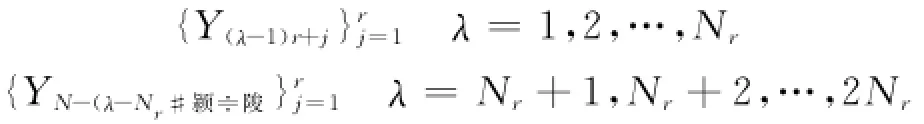
3）对每个小区间λ,拟合局部趋势¯Yλ（j）,并计算滤去该趋势后的序列的二阶原点矩

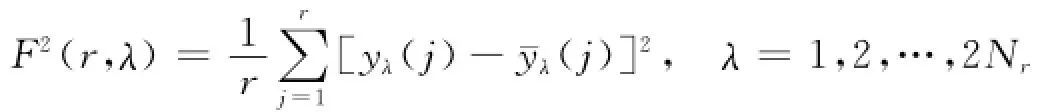
4）计算q阶波动函数：

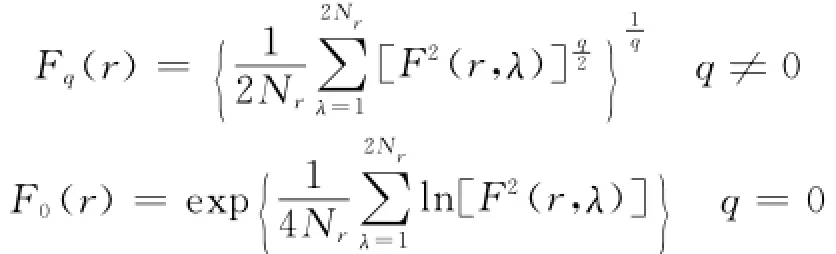
5）对于每个确定的q值,求出相应的Fq（r）,并将r与Fq（r）的关系绘制在双对数坐标系上,其图像的斜率即为q阶Hurst指数h（q）.

对于单一分形序列,其h（q）随着q的变化始终为一常数；对多重分形序列,h（q）为q的函数.

6）利用Lengendre变换,得到多重分形谱参数：

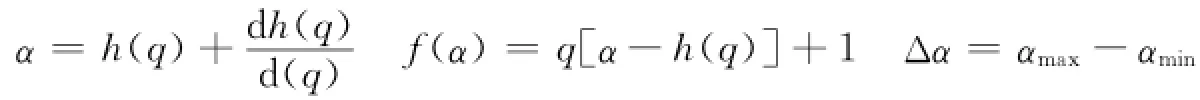
3 结果与讨论

3.1 盒维数的结果分析

计盒维数D,越接近于1,数据列结构越稀疏,反之,结构越紧密.可表征PM10浓度在时间轴上分布的标度不变结构,表明其统计分布规律.

图2为不同阀值Th下PM10浓度在时间轴上分布的盒维数.

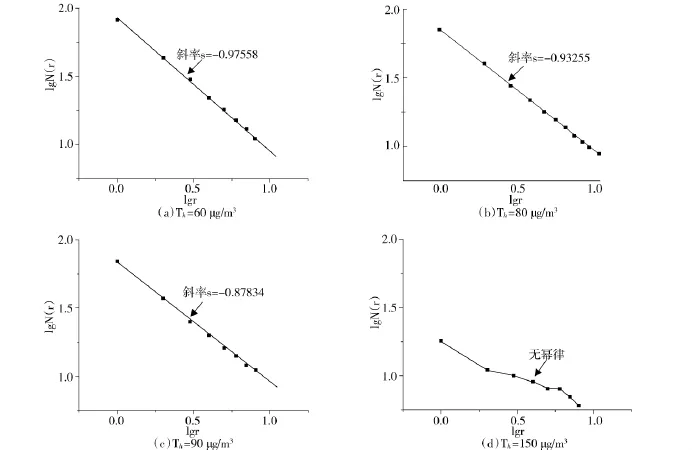
图2 不同阀值Th下PM10浓度在时间轴上分布的盒维数

由图2可见,当阀值Th分别取60,80,90时,高于阀值Th的PM10浓度的盒维数分别为0.975 58,0.932 55,0.878 34.盒维数D随着阀值Th的增加呈现下降的趋势；当阀值为150时,高于阀值的浓度点在整个时间尺度范围内的线性关系消失.此时,标度不变分形结构消失.

在统计上,盒维数的所表现出的标度不变性可用来预测PM10浓度.由于不同的时间尺度范围内PM10浓度点的数量具有相同的幂律分布规律,所以,对给定的阀值Th,可由盒维数D计算某一时间尺度范围内高于阀值Th的浓度点的数量

N（r）≈rD.

3.2 MF－DFA结果分析

利用MF－DFA方法,对PM10浓度进行计算,绘出α－f（α）多重分形谱图见图3,

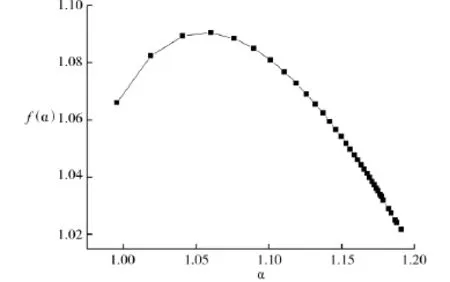
图3a－f（a）多重分形谱

称为奇异指数,它刻画子集的奇异程度；f（α）称为多重分形谱,其本质为分形集中与α相关的子集的Hausdorff维数.Δα描述多重分形的强弱程度,其值越大,多重分形特征越显著.

由图像可知,α－f（α）曲线呈现上凸趋势,图像开口向下,Δα＝0.194,说明太原市春季PM10日平均浓度的多重分形特征不明显.

［1］Falconer.K.Fractal geometry：Mathematical foundations and Applications［M］.John Wiley.Sons.Inc,New York,1990

［2］邵龙义,沈蓉蓉.北京市PM10粒度分布分形维数特征［J］.中国矿业大学学报,2008,37（3）：407－411

［3］杨书申,邵龙义.上海市大气可吸入颗粒物的粒度分布分形维数特征［J］.中国环境科学,2007,27（5）：594－598

［4］吴生虎,史 凯.成都市一次重雾霾期间PM10自组织演化的分形特征及DFA分析［J］.安全与环境学报,2014,14（5）：286－291

［5］黄 毅,刘春琼.灰霾消散前后PM10浓度大幅波动的多重分形分析［J］.环境科学与技术,2016,39（1）：140－146

［6］曾超益,袁德辉.含参变量Cantor集的Hausdorff测度［J］.数学杂志,2011,31（4）：729－736

The Fractal Dimension and MF－DFA Analysis of PM10in Taiyuan Spring

JIN Yanling
（Dept.Public Foundation,Business College of Shanxi University,Taiyuan 030031,China）

In Taiyuan city on March 1,2016to May 31,basis on the data of average daily PM10concentration.Using the box dimension in fractal geometry index quantitative characterization concentration variation characteristics given under a certain threshold,the prediction formula of high concentration of PM10in probability and using the method of multifractal eliminate fluctuation trend analysis on the multifractal characteristics of PM10concentration changes,found that Taiyuan city spring multifractal characteristics of PM10concentration change is not obvious

fractal；box dimension；MF－DFA analysis；PM10

1672－2027（2016）04－0060－03

0172

A

2016－09－12

山西省教育科学“十三五”规划课题（GH16173）.

金艳玲（1981－）,女,吉林通辽人,硕士,山西大学商务学院讲师,主要从事几何研究.