目标机动频率自适应估计的UKF滤波算法研究*
2016-02-24董霓徐俊艳
董霓,徐俊艳
(北京电子工程总体研究所,北京 100854)
导航、制导与控制
目标机动频率自适应估计的UKF滤波算法研究*
董霓,徐俊艳
(北京电子工程总体研究所,北京 100854)
研究了反弹道导弹中机动目标的拦截问题,提出了一种基于机动频率自适应的UKF滤波估计算法,将实时估计得到的机动频率应用于目标运动状态的滤波过程中,从而对目标运动信息进行快速而有效的估计。仿真结果表明,这种自适应估计算法,较固定机动频率的滤波算法,有较快的目标估计速度,较高的目标估计精度,能有效的跟踪和应对目标机动加速度的快速变化,有效避免了由于不能及时跟踪的目标运动信息而导致较大脱靶量的现象。
机动频率;自适应估计;目标跟踪;UKF滤波;机动目标拦截;机动运动模型
0 引言
随着反导技术的日益成熟,弹道导弹的突防能力也与日俱增。导弹为了增大突防的成功率,有可能根据实际战场情况,进行一定的机动来躲避拦截方导弹。因此,对于机动目标的拦截问题将成为拦截弹制导控制系统面临的主要问题。为了准确拦截敌方导弹,就要对目标的运动变化进行估计。目前,描述目标运动或机动方式的模型有Singer模型[1-2]、“当前”统计模型[3]、适用于强机动的Jerk模型[4]等。一般来说,机动目标的运动估计过程是一种自适应滤波过程,需要根据实时量测信息的变化估计出这些模型中的参数,也就是目标的机动参数。通常,估计目标机动的难点在于其不确定性,引起该不确定的因素主要有2个:一是来自于机动形式的不确定性;二是来自于量测信息的不确定性。
弹道导弹的拦截在控制系统设计方面有2个主要问题:一是对于目标运动状态的信息估计;二是制导控制方法研究。其中,有效的目标运动状态估计是保证制导精度的前提。在导引头的探测精度很难进一步提高的情况下,通过软件方法提高目标运动状态的估计精度是一个较为有效的手段。
1 常见的估计模型及其缺陷
由于本文考虑机动频率的自适应算法对目标机动运动模型估计精度的影响,传统较为简单的匀速模型和匀加速模型中不含有机动频率参数,在这里不做过多研究。
1.1 Singer模型
Singer模型采用三阶的运动模型,与匀加速模型(简称CA模型)不同,它引入一个机动频率参数α。在Singer模型中目标加速度采用输入为白噪声的一阶时间相关过程为
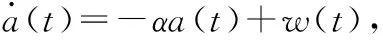
(1)
并有连续时间下Singer模型的状态方程表示为
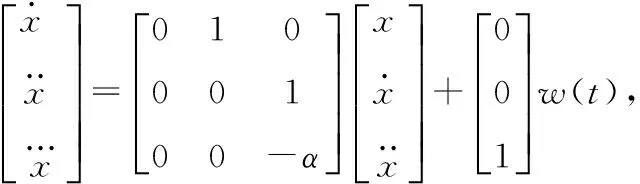
(2)

Singer模型虽然简单,但是可以较好地跟踪目标的随机机动运动,足以应对一般形式的目标机动运动,Singer模型[2]跟踪低频机动目标的能力明显要优于跟踪高频机动目标。但是Singer模型有一个严重的缺陷,存在一定的稳态误差[4]。
1.2 CS模型
CS模型[3](又称“当前”统计模型)在Singer模型的基础上,增加了非零均值的加速度项,使得在滤波估计目标状态的同时,还可以通过辨识目标机动加速度的均值,实时对其进行修正,并将修正结果反馈到下一时刻的卡尔曼滤波过程中。连续时间下,“当前”统计模型的状态方程为
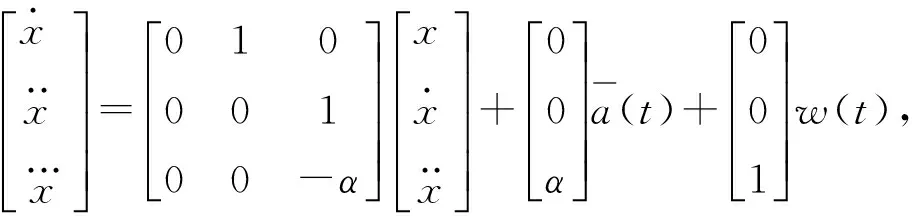
(3)
与Singer模型相比较,“当前”统计模型引入的非零均值加速度项能有效的改进目标机动的估计精度。并且“当前”统计模型具有一个显著优势,即引入的非零均值加速度项使其消除了Singer模型带来的稳态误差,使得“当前”统计模型的稳态误差为0。
1.3 Jerk模型
Jerk模型在Singer模型的基础上,又增加了一维状态变量,引入加加速度,Kishore认为各种机动模型不能准确跟踪复杂机动运动的一个原因就是状态变量的导数阶数不足,因此,Jerk模型采用四阶导数,对目标的复杂机动运动进行加加速度的估计,从而达到提高目标跟踪精度的效果。Jerk模型的状态方程[5]为
(4)
式中:w(t)意义也与Singer模型中类似。
2 基于UKF滤波的机动频率自适应算法
2.1 机动频率自适应算法
第1节提到的几种典型模型均依赖于机动频率参数α,在实际作战中,对目标机动频率无从得知,而假定机动频率为常值的做法显然是不符合实际情况的。有一些学者也对变机动频率算法进行了的相关研究。
文献[6]的研究结果表明,利用残差进行机动频率自适应估计并没有起到较为明显的作用,仅在误差峰值处较固定机动频率的算法有小幅度的性能提升。文献[7]提出的机动频率自适应方法主要依赖于判断滤波残差是否符合零均值的正态分布来对目标机动进行判断,机动频率的调节采用神经网络的寻优算法进行调整,但仿真结果表明对于加速度的估计没有明显的作用。文献[8]考虑到机动频率对系统状态矩阵和滤波增益阵的不同影响,设计了一种双机动频率的滤波算法,但在实际应用中,这种算法在一些条件下,滤波容易发散。文献[8]提出的一种机动模型,将机动频率当做非零均值的白噪声加入在Singer模型或Jerk模型中,在原有模型基础上又增加一阶,对弱机动运动信息能较为准确地估计,但是在应对剧烈的机动运动情况时,滤波计算容易出现方差阵发散的情况。针对以上问题,本文根据文献[9]基于加速度方差自适应算法,考虑到加速度方差自适应算法对机动目标的跟踪精度的影响,针对“当前”统计模型提出了一种机动频率和加速度方差同时自适应算法,本文在其机动频率自适应的基础上,将其推广到Singer,Jerk等模型中。依据当前时刻与前一时刻状态估计的信息,对目标机动进行判断,从而达到通过对当前时刻机动频率α的估计来实现自适应滤波。该算法在机动加速度、速度、位置的滤波上均有明显的优势。
Singer模型中,假定目标加速度a(t)的自相关函数为
(5)
式中:σa为目标加速度方差。
式(1)经离散化得到:
a(k+1)=e-αTa(k)+w(k+1),
(6)
对式(6)两边同时取期望,进行数学运算,可得
E[a(k+1)]=E[e-αTa(k)+w(k+1)]=E[e-αTa(k)]+E[w(k+1)]=E[e-αTa(k)].
(7)
由于卡尔曼滤波是最小均方意义下的滤波方法,则有
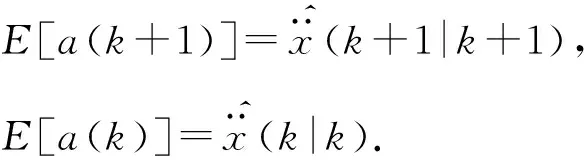
(8)
代入式(7),得到
(9)
对式(9)进行变换有
(10)
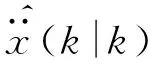
类似于Singer模型算法,目标加加速度j(t)的指数自相关函数为
(11)
用随机过程描述目标加加速度的变化率为
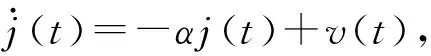
(12)
将式(12)经离散化,同时取数学期望,可得
E[j(k+1)]=E[e-αTj(k)+v(k+1)]=E[e-αTj(k)]+E[v(k+1)]=E[e-αTj(k)],
(13)
由式(13)可推导出,Jerk模型的机动频率估计表达式为
(14)
2.2 UKF滤波算法
由于引入机动频率自适应算法,式(10)和式(14)使得机动模型在计算过程中呈现非线性。因此,在对模型进行滤波的时候,普通的卡尔曼滤波不再适用,下面考虑采用UKF非线性卡尔曼滤波算法。
UKF算法是利用UT变换,确定在估计点附近的采样点,利用这些采样点表示的高斯密度来近似状态的概率密度函数,这些采样点的均值和方差等于原状态分布的均值和方差。这样使非线性变化后的均值和方差精度具有至少二阶精度。
随机变量X在不同时刻的UKF算法基本步骤如下[10-13]:
步骤1:获得一组Sigma点集
(15)
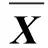
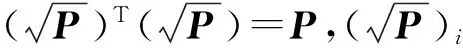
步骤2: 对(2n+1)个Sigma点集进行一步预测
X(i)(k+1|k)=f[k,X(i)(k|k)],
(16)
式中:i=1,2,…,2n+1;函数f为系统状态量的非线性变换。
步骤3: 计算状态变量的一步预测及协方差矩阵
(17)
式中:P(k+1|k)为一步预测方差阵;Q阵为状态方程系统噪声方差阵;各采样点权值ω(i)的计算表达式如下:
(18)
式中:下标m表示均值;c表示协方差;上标为采样点序数;参数λ=γ2(n+κ)-n为一个缩放比例参数,参数γ的取值范围为0.000 1≤γ≤1;κ和β为待选参数[14]。
步骤4: 根据一步预测值,使用UT变换,得到新的Sigma点集
(19)
式中:
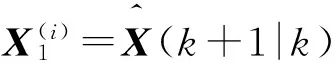
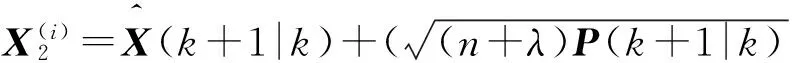
(20)
步骤5: 将步骤4得到的Sigma点集代入观测方程,其中h为观测方程函数。
Z(i)(k+1|k)=h[X(i)(k+1|k)].
(21)
步骤6: 将步骤5计算得到的观测预测值加权得到系统的预测值的均值和方差
(22)
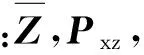
步骤7: 计算Kalman增益矩阵
(23)
步骤8: 计算系统的状态更新和协方差更新
(24)
3 数学建模及仿真结果
3.1 模型建立
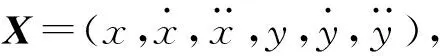
x(k+1)=f(x(k),α,k)+w(k),
z(k+1)=Hx(k+1)+v(k+1),
(25)
式中:
H=(1,0,0),
(26)
式(26)为进行目标机动估计滤波的系统状态方程和量测方程。
3.2 仿真条件及结果
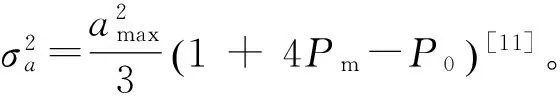
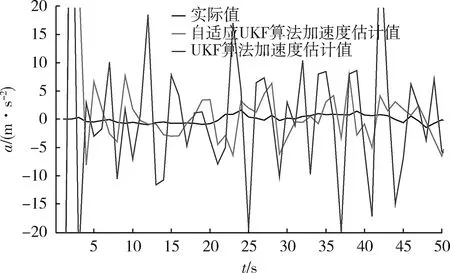
图1 滤波估计的加速度轨迹Fig.1 Acceleration curve of filtering estimation
可以看出,自适应机动频率算法有效的对目标加速度进行了估计,滤波误差明显小于常值机动频率的估计算法。尽管Singer模型中假定的机动运动形式可以概括一类较广泛的机动运动形式。但是实际作战中,仍会存在其他机动方式。
为了验证机动频率自适应算法的广泛应用性,下文仿真考虑具有实际应用性的正弦加速度,并选取实际目标机动加速度形式为
a(t)=30sin[(2π/100)t)+20sin[(2π/120)t],
经过仿真可以发现,基于机动频率自适应的UKF滤波算法不仅对符合模型一阶马尔可夫过程的加速度机动有很好的估计作用,而且该算法对于其他加速度模型也具有较强的适应性。根据前面推导得出的自适应机动频率的估计算法,以及机动目标运动系统的模型,分别采用机动频率自适应UKF滤波算法和普通UKF算法进行仿真分析。为方便起见,考虑单方向上直角坐标的情况,自适应机动频率算法与UKF滤波算法仿真结果如下。
图2为2种算法对目标加速度的跟踪曲线对比图,可以看到,普通的UKF算法滤波的加速度估计在加速度真值附近处有较大幅度的波动与偏差,而自适应机动频率UKF滤波算法在整个仿真过程中滤波值较为稳定,偏差波动不大,加速度变化较快处,跟踪精度较高,具有一定的滤波优势。
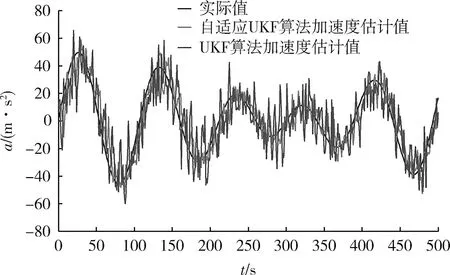
图2 滤波估计的加速度轨迹Fig.2 Acceleration curve of filtering estimation
图3反映了2种滤波算法对应的加速度误差、速度误差、位置误差,可以明显看到,自适应算法不仅在加速度项误差上有明显优势,速度偏差相较普通算法也较为平缓。在几个采样间隔时间点上,速度误差有相对较大的波动,原因是在该采样间隔前后,机动频率自适应的变化值较为明显,滤波增益由于接受到较大信息正处于调节阶段。从位置误差曲线可以看出,自适应机动频率算法较有优势,误差值波动较小,滤波过程处于较为稳定的状态。
图4为自适应滤波算法的机动频率曲线,可以看到,自适应算法有别于以往的固定机动频率的算法,在滤波过程中,根据估计的目标信息,机动频率参数不断更新,从而更好的跟踪目标,并进行目标运动状态信息的估计。
对Jerk模型,机动加速度形式与前文一致,对时间求一阶导数得到目标机动的加加速度机动形式为j(t)=0.6πsin[(2π100)t]+0.33πsin[(2π/120)t],
其他初始条件与Singer模型相同,有Jerk模型的仿真结果如图5所示。本文提出的自适应机动频率UKF滤波算法在状态估计上有明显的提高。
图3 2种滤波算法的跟踪偏差Fig.3 Error of two filtering algorithms

图4 自适应滤波算法的机动频率变化曲线Fig 4 Maneuvering frequency curve of adaptive filtering algorithm
表1,2为2种模型仿真结果数据分析,从表中数据可以明显看出自适应机动频率算法偏差的均值和方差都优于普通UKF滤波算法。对于Jerk模型,滤波效果在均值体现不太明显,但整体偏差的方差小于普通滤波,说明具有机动频率自适应的滤波算法应对机动变化程度大的系统,其滤波估计能力越好,并且滤波偏差幅度明显较小[15]。
对比表1,2数据统计结果,可以发现,2种模型在位置上的估计没有太大的差异,自适应估计算法略优于普通的滤波算法。在速度信息和加速度信

图5 Jerk模型仿真结果Fig.5 Jerk model simulation result
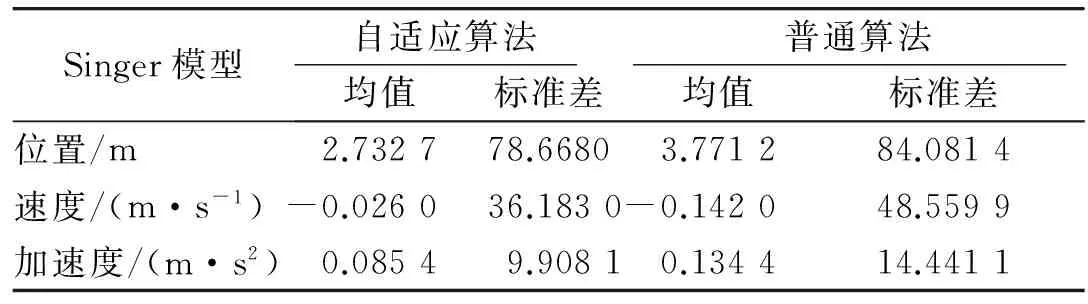
表1 Singer模型滤波偏差均值和方差Table 1 Mean and standard deviation of error by Singer model filtering result
息的估计结果上,Singer模型得到的数据均值和方差明显优于Jerk模型。因此,对于本文提出的正弦机动形式,Singer模型的估计结果优于Jerk模型,但对于其他机动形式,还需更为深入的研究。
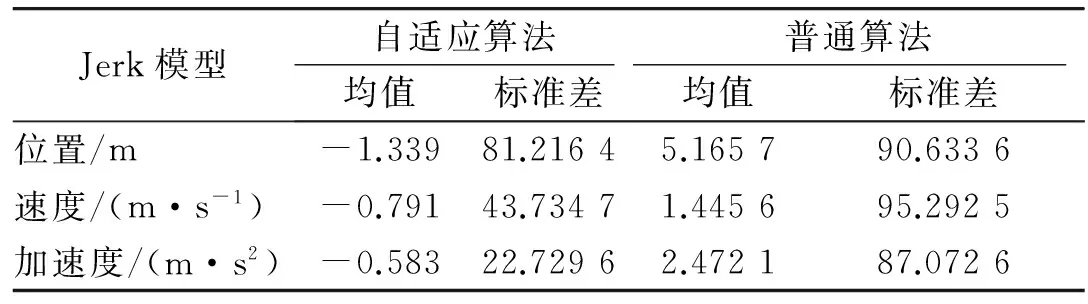
表2 Jerk模型滤波偏差均值和方差Table 2 Mean and standard deviation of error by Jerk model filtering result
4 结束语
在实际的目标拦截中,很难预先知道目标的运动信息,其中就包括机动频率α的精确值。因此,以一预先固定机动频率的值对目标运动信息进行估计是不准确的。从仿真结果来看,本文提出的具有自适应能力的机动频率估计算法可以有效的对目标机动频率进行实时估计,并且将估计结果实时地反映到滤波过程中去,可以有效地对目标加速度等信息进行快速而准确的估计,滤波偏差具有较小均值和方差等统计特性,有利于为精确制导提供较为准确的目标跟踪信息,为制导律的实现打下了坚实的基础,避免了由于不能及时跟上目标信息导致脱靶量较大的情况。
[1] LI R X, JILKOV V P . A Survey of Maneuvering Target Tracking: Dynamic Models[C]∥SPIE, 2000, 4048:212-236.
[2] SINGER R A. Estimating Optimal Tracking Filter Performance for Manned Maneuvering Targets [J]. IEEE Trans. on Aerospace and Electrical System, 1970, 6(7): 473-483.
[3] ZHOU H, KUMAR K S P. A “Current” Statistical Model and Adaptive Algorithm for Estimating Maneuvering Targets [J]. AIAA Journal of Guidance, 1984, 7(5): 596-602.
[4] 周宏仁, 敬忠良, 王培德. 机动目标跟踪[M].北京:国防工业出版社, 1991. ZHOU Hong-ren, JING Zhong-liang, WANG Pei-de, Maneuvering Target Tracking[M].Beijing: National Defense Industry Press, 1991.
[5] MEHROTRA K, MAHAPATRA P R. A Jerk Model for Tracking Highly Maneuvering Targets [J]. IEEE Trans. on Aerospace and Electrical System, 1997, 33(4): 1094-1105.
[6] 王军政, 沈伟, 赵江波. 机动目标跟踪中机动频率的自适应调整 [J].北京:北京理工大学学报, 2007 (1):38-41. WANG Jun-zheng, SHEN Wei, ZHAO Jiang-bo. Adaptive Adjustment of Maneuvering Frequency in Target Tracking[J]. Transactions of Beijing Institute of Technology,2007(1):38-41.
[7] 刘昌云, 刘进忙, 陈长兴, 等. 机动目标跟踪的机动频率自适应算法[J]. 控制理论与应用,2004 (6):961-965. LIU Chang-yun, LIU Jin-mang, CHEN Chang-xing,et al. Maneuvering Frequency Adaptive Algorithm of Tracking a Maneuvering Object[J]. Control Theory & Applications, 2004(6):961-965.
[8] 石书生, 曾芳玲. 一种双机动频率自适应算法研究[J]. 计算机工程与应用, 2012, 48(4):152-154. SHI Shu-sheng, ZENG Fang-ling. Adaptive Algorithm for Dual Maneuvering Frequency[J]. Computer Engineering and Applications, 2012, 48(4):152-154.
[9] 钱广华, 李颖, 骆荣剑.机动目标跟踪中一种机动频率和方差自适应滤波算法[J]. 雷达学报, 2013, 13(15):257-264. QIAN Guang-hua, LI Ying, LUO Rong-jian. One Maneuvering Frequency and the Variance Adaptive Filtering Algorithm for Maneuvering Target Tracking[J]. Journal of Radars,2013, 13(15):257-264.
[10] 罗笑冰, 王宏强, 黎湘, 等. 机动目标跟踪α-jerk模型[J]. 信号处理, 2007, 23(4):481-484. LUO Xiao-bing, WANG Hong-qiang, LI Xiang,et al. A α-jerk Model for Tracking Maneuvering Targets[J]. Signal Processing, 2007, 23(4):481-484.
[11] 何友,修建娟,张晶炜,等. 雷达数据处理及应用[M]. 北京:电子工业出版社,2009. HE You, XIU Jian-juan, ZHANG Jing-wei,et al. Radar Data Processing with Applications[M].Beijing: Publishing House of Electronics Industry, 2009.
[12] JULIER S J, UHLMANN J K. The Scaled Unscented Transformation[C]∥The American Control Conference, Anchorage, 2002,6:4555-4559.
[13] JULIER S J, UHLMANN J K, DURRANT-WHYTE H F. A New Method for the Nonlinear Transformation of Means and Covariances in Filters and Estimators [J]. IEEE Trans. on Automatic Control, 2000,45(3):477-482.
[14] WAN E A, MERWE R V. The Unscented Kalman Filter for Nonlinear Estimation[C]∥IEEE Symposium 2000(AS-SPCC), Lake Louise, Alberta, Canada, Oct. 2000:153-158.
[15] 王芳, 冯新喜, 李鸿艳. 一种新的自适应滤波算法[J]. 现代雷达, 2003, 7(7): 23-35. WANG Fang, FENG Xin-xi,LI Hong-yan. A Novel Adaptive Filtering Algorithm[J]. Modern Radar, 2003, 7(7): 23-35.
Maneuvering Target’s UKF Filter Algorithm with Adaptive Maneuvering Frequency Method
DONG Ni,XU Jun-yan
(Beijing Institute of Electronic System Engineering, Beijing 100854,China)
An adaptive algorithm for estimating maneuvering frequency parameterin intercepting maneuvering target is proposed based on unscented Kalman filter (UKF) algorithm, and this algorithm enhances the estimated accuracy of target movement information by obtaining accurate real-time value of maneuvering frequency. The simulation results show that, this adaptive algorithm could perform efficiently and rapidly and track changes of target acceleration precisely when compared with the normal filter method. This method can avoid the longer miss distance owning to failure of trackingtarget movement information.
maneuvering frequency; adaptive estimation; target tracking; unscented Kalman filter(UKF); maneuvering target interception; maneuvering models
2015-10-30;
2016-02-19
有
董霓(1991-),女,陕西西安人。硕士生,主要研究方向为导航制导与控制。
10.3969/j.issn.1009-086x.2016.06.013
TJ765.3;TP301.6;TP391.9
A
1009-086X(2016)-06-0072-08
通信地址:100854 北京142信箱30分箱
E-mail:dongnilucky@163.com
