输电线路覆冰脱落参数影响研究

李嘉祥，李宏男，付兴

(大连理工大学建设工程学部, 辽宁省大连市116024)

输电线路覆冰脱落参数影响研究

李嘉祥，李宏男，付兴

(大连理工大学建设工程学部, 辽宁省大连市116024)

覆冰脱落会造成导线断股、金具破坏和闪络等事故，是输电线路的常见灾害之一。为了研究覆冰脱落的振动机理,通过ANSYS有限元软件建立了输电线路模型，考虑覆冰刚度影响，使用生死单元技术模拟了2种典型的覆冰脱落形式，即单导线受冲击荷载脱冰和分裂导线单子导线脱冰。通过数值模拟研究了线路参数和外部荷载对导线脱冰的影响，结果表明：(1)单导线受冲击荷载脱冰在跨度较大时应考虑风荷载的影响；(2)脱冰率和跳跃高度随冲击荷载的增大而增大；(3)分裂导线单子导线脱冰能够加速分裂导线的脱冰过程，并且应考虑风荷载的影响；(4)子导线的数目与分布对脱冰率有影响；(5)在跨中附近布置间隔棒有利于减小最大跳跃高度；(6)不考虑覆冰刚度的模拟结果偏于不安全。研究成果可以为输电线路的设计提供参考。

覆冰脱落; 覆冰刚度; 脱冰率; 跳跃高度

0 引 言

覆冰脱落会引起导线强烈振动，是输电线路的主要灾害之一，对其振动机理进行研究很有必要。目前，对覆冰脱落问题的研究方法分为3类：现场观测、模型试验及有限元数值模拟。覆冰脱落具有很大的随机性，因此观测结果很少；模型试验成本大且很难模拟覆冰脱落的真实情况；有限元数值模拟是目前研究覆冰脱落问题最主要的手段，应用广泛。

国内王昕和楼文娟[1]通过建立三跨导线力学模型对脱冰参数进行了研究；陈勇等[2]通过对比数值模拟与模型试验结果证明了有限元模拟研究的有效性；国外Roshan和McClure[3]研究了输电线路脱冰的影响参数。以上研究都是针对单根导线进行的，但国内外超高压和特高压线路基本采用的都是分裂导线。严波等[4]通过商用软件ABAQUS研究了分裂导线脱冰情况，得到了脱冰跳跃高度的近似公式；沈国辉等[5]研究了单子导线脱冰引起的动力反应，认为间隔棒布置对脱冰跳跃有显著的抑制作用；Kollar和Farzaneh[6-7]研究了冰厚、子导线数量和间隔棒对分裂导线脱冰的影响。在上述提到的研究中均只考虑了覆冰的质量，没有考虑覆冰的刚度，忽略了脱冰引起的振荡导致覆冰连续破碎脱落的情况。Kalman等[8]首次提出了覆冰的破坏准则，研究了冲击荷载作用下地线覆冰破碎脱落的过程；陈科全等[9-12]提出了覆冰的拉伸破坏准则，研究了单档和连续档导线的机械除冰影响参数，并提出了一种自动除冰装置。上述研究考虑了覆冰刚度，但只针对导地线受冲击除冰，且均未考虑脱冰过程中风荷载及气动力阻尼影响。《110～750 kV架空输电线路设计规范》中明确规定计算覆冰荷载时，需要考虑风荷载的作用；而且对于输电导线，气动力阻尼对导线的影响远远大于结构阻尼。

综上所述，已有研究没有充分考虑覆冰刚度、风荷载和气动力阻尼对覆冰脱落的影响，还缺乏针对单子导线覆冰脱落引起振荡，进而导致覆冰连续破碎脱落的研究。

鉴于此，本文采用通用有限元软件ANSYS建立单导线和分裂导线模型，考虑覆冰刚度、风荷载和气动力阻尼，使用生死单元技术模拟导线脱冰过程，分析单导线受冲击荷载脱冰和分裂导线单子导线脱冰的情况，研究线路参数和外部荷载的影响，得到具有实际意义的结果。

1 覆冰导线有限元建模

冲击荷载作用在导线上，或导线上部分覆冰发生脱落都可引起导线振动，导致部分覆冰脱落。在此过程中，导线的弹性势能转化为重力势能，使振动更加剧烈，并有可能引起导线覆冰连续脱落[8,13]。由于上述覆冰脱落过程属于强非线性振动，很难通过解析方法来描述并准确获得覆冰导线的运动状态。使用有限元建模能够准确地模拟覆冰脱落过程，得到覆冰脱落过程中导线的位移和应力，从而为输电线路的设计提供参考。

1.1 导线模型参数

输电导线属于典型的悬索结构，满足悬索结构的动力特性，即在运动过程中只受拉，不受压。本文建立了单档单导线和分裂导线模型。由于杆塔刚度对导线脱冰的影响不大，故忽略铁塔作用，导线两端采用固结[1]。在ANSYS中的LINK10单元通过设置单元的关键选项，实现只受拉、不受压的状态，用来模拟导线。设置初始应力进行导线找形，导线的具体参数如表1所示。

表1 导线的机械参数
Table 1 Mechanical parameters of conductor

1.2 间隔棒模型参数

间隔棒是分裂导线特有的金具，用来保持子导线之间的距离，防止在环境荷载或者电磁力作用下发生碰线。本文对间隔棒采用如下假设：(1)刚性间隔棒假设，即间隔棒不发生变形；(2)间隔棒与导线的连接点无相对位移。使用LINK8单元模拟间隔棒，不同分裂数的间隔棒如图1所示，图中数字为子导线编号，文中分裂间距都为0.5 m。

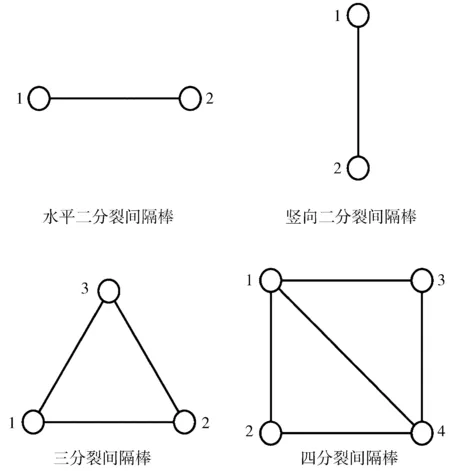
图1 间隔棒模型Fig.1 Model of spacers

1.3 覆冰模型参数

受自然条件和线路走向等因素的影响，导线覆冰截面可能呈现各种不规则形状[14]。我国输电线路设计手册[15]中的覆冰是指环形截面的覆冰，其他学者在研究导线覆冰脱落时采用了环形覆冰假设[4-8]，因此本文也假设导线覆冰为环形。本文采用与导线单元共节点的BEAM188单元模拟覆冰。根据以往研究[7-12]可知：冰的破坏模式受应变率影响，且在脱冰的过程中覆冰表现为脆性破坏。本文采用Kalman等[8]在论文中使用的覆冰参数和破碎准则，即覆冰的弹性模量为10 GPa，质量为900 kg/m3。冰单元在积分点的塑性应变超过10-10时，视为覆冰破碎，发生脱落。使用生死单元来模拟覆冰脱落的过程。

1.4 风荷载模拟参数

在以往的研究里，很少在覆冰脱落的过程中考虑风荷载的作用，但现实的情况是：发生覆冰脱落时，往往伴有风荷载。我国《110～750 kV架空输电线路设计规范》规定在计算覆冰荷载的同时要考虑相应风速的风荷载，因此在研究覆冰脱落的过程中，考虑风荷载的作用是必要且合理的。

风荷载具有时间和空间随机变化的特征，可以用式(1)表示：

(1)

风荷载的模拟与我国的《建筑荷载设计规范》一致，采用Davenport谱。假定脉动风速的均值为0，使用谐波叠加法模拟风荷载。图2为模拟风谱与目标风谱的比较；图3为生成的离导线左端20 m处(点52)的模拟风速，具体的模拟参数为：B级地面粗糙度，离地10 m高度处的基本风速为10 m/s，高度为 45 m；不考虑风的尾流效应，将不同时刻的风荷载换算成节点荷载，加载到导线的节点上，模拟风荷载对导线的作用。

图2 风谱Fig.2 Wind spectrum

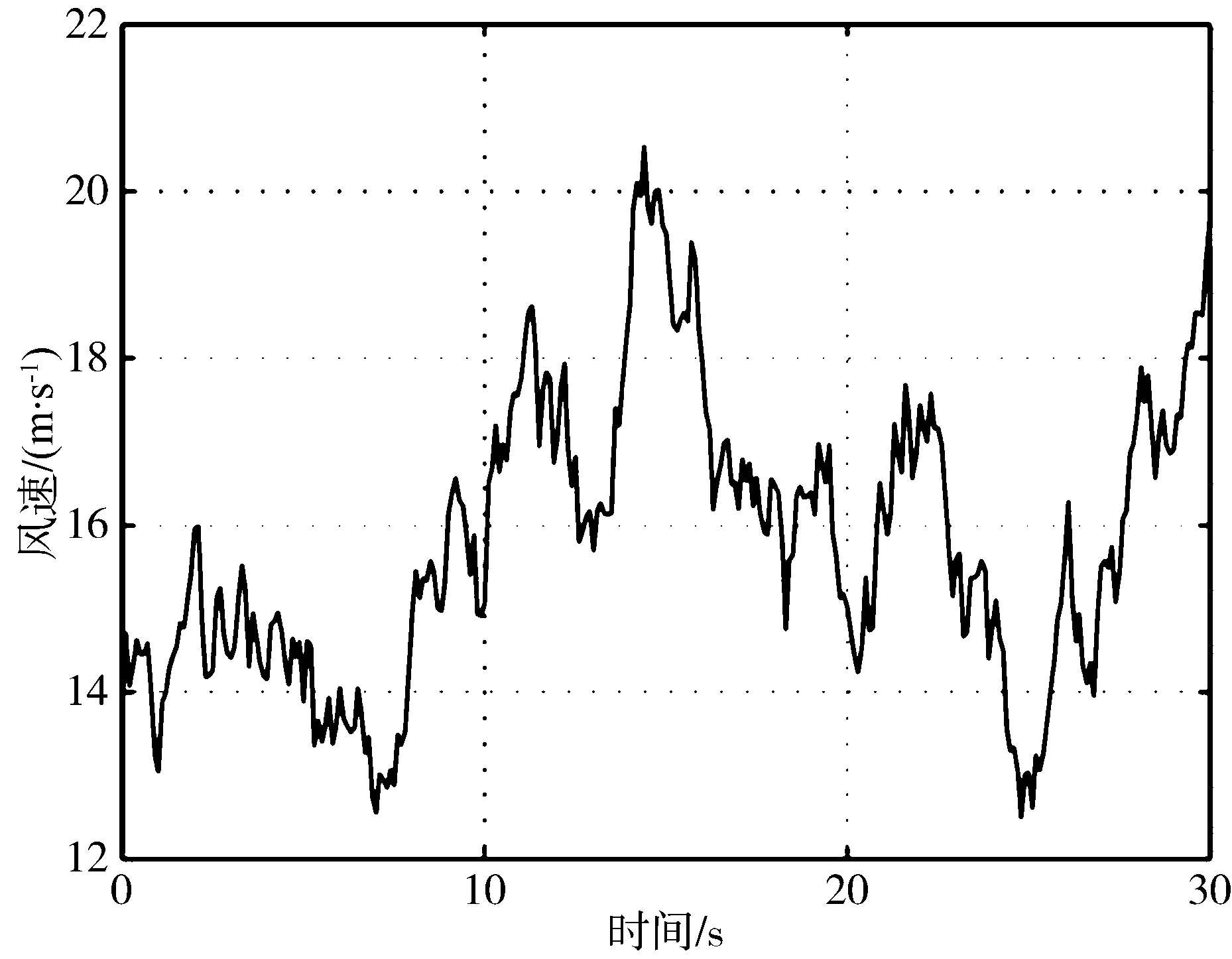
图3 点52处模拟的风速Fig.3 Simulated wind speed at point 52

1.5 导线阻尼计算方法

导线的阻尼分为结构阻尼和气动力阻尼。有限元模型采用瑞雷阻尼模拟结构阻尼，瑞雷阻尼的计算如式(2)所示：

C=αM+βK

(2)

式中：C、M和K分别为导线的阻尼矩阵、质量矩阵和刚度矩阵；α和β为与结构自振频率和阻尼比相关的参数。覆冰导线的α取0.1，β取0[9]。

气动力阻尼受很多因素影响，如覆冰形状、初始攻角、气动力曲线等。本文采用如下简化：假设覆冰截面为圆环，因此也就不存在随攻角变化的气动力曲线。气动力阻尼计算如式(3)所示：

Fd=-0.5CDρv2dle

(3)式中：CD为阻力系数，取1.1[16]；ρ为空气密度，取1.29 kg/m3；v为导线节点的速度；d为导线直径，对覆冰导线取覆冰与导线总体直径，对裸导线取导线直径；le为单元长度。气动力阻尼力以节点力的形式加载到节点上，负号表示与导线的运动方向相反。

导线脱冰有多种形式，本文研究了2种典型情况：单导线受冲击荷载脱冰和分裂导线单子导线脱冰。这2种脱冰都是在3.0 s时发生。

2 单导线受冲击荷载脱冰

覆冰导线受冲击荷载脱冰是机械破冰的主要方式之一。因为分裂导线各子导线受相同冲击作用后运动状态是同步的，等同于单导线受冲击，故本文只研究单导线受冲击。

2.1 单元数目的影响

对初始水平张力为35 316 N、跨度为100 m的导线，在距导线左端6 m处作用10 kN的冲击荷载，加载时间和卸载时间均为0.001 s ，如图4所示。

图4 导线受冲击荷载示意图Fig.4 Schematic sketch of shock-load on conductor

有限元模拟的准确性与单元划分有很大关系，为了能够更准确地模拟覆冰脱落的过程，将导线划分为不同单元长度进行脱冰计算，不考虑风荷载和气动力阻尼，结果如图5所示。根据有限元原理可知，导线划分的单元长度越小，计算结果越真实，但计算效率越低。从图5可以看到，脱冰率与导线单元的划分有很大关系：单元数量较少时，每档单元划分数目与脱冰率成正比；当单元数目为250和300个时，计算结果很接近，说明计算结果趋于稳定。综合考虑计算准确度和计算效率，导线划分为250个单元，即单元长度为0.4 m较为合适。

图5 脱冰率与单元数目的关系Fig.5 Relationship between ice-shedding rate and element number

2.2 风和气动力阻尼的影响

冲击荷载为12 kN时，风和气动力阻尼对脱冰率的影响如图6所示。跨度为100 m时，随着风速的变化，脱冰率基本不变，说明跨度较小时，风和气动力阻尼对脱冰率的影响可以忽略。当跨度为300 m时，随着风速的增加，脱冰率增加。不考虑风荷载时，脱冰率为28.9%；风速为10 m/s时，脱冰率达37.9%；当风速为15 m/s时，脱冰率增达60.9%。跨度为300 m时，气动力阻尼的影响开始增大。不考虑风荷载，仅考虑气动力阻尼，脱冰率从28.9%减小为21.5%；风速为10 m/s，考虑气动力阻尼时，脱冰率从37.8%减小为28%；风速为15 m/s，考虑气动力阻尼时，脱冰率从60.9%减小为59%。综上可知，风荷载的影响随着跨度的增大而增大，随着风速的增大而增大；气动力阻尼的影响随着跨度的增大而增大，但当脱冰率较高，即脱冰跳跃行为比较剧烈时，影响变小。

2.3 冲击荷载幅值的影响

冲击荷载幅值不仅与脱冰率有关，而且对导线的跳跃高度也有影响。冲击荷载分别取10，20，30及40 kN，从图7中可明显看出脱冰率随着冲击荷载的增大而增大，直至100%。图8给出了不同冲击荷载作用下的最大跳跃高度。冲击荷载为10 kN时，最大跳跃高度为0.22 m；冲击荷载为20 kN时，最大跳跃高度为0.37 m；冲击荷载为30 kN时，最大跳跃高度为0.62 m；冲击荷载为40 kN时，最大跳跃高度为0.67 m。可以看出，导线的最大跳跃高度随着冲击荷载幅值的增大而增大。

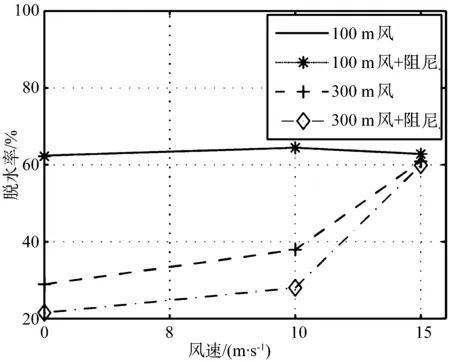
图6 风速与脱冰率的关系Fig.6 Relationship between wind speed and ice-shedding rate

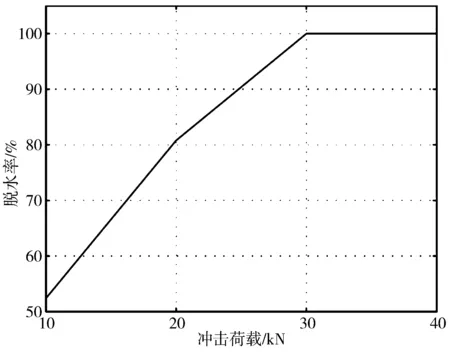
图7 冲击力与脱冰率的关系Fig.7 Relationship between shock-load and ice-shedding rate

3 分裂导线单子导线脱冰

在自然条件下，或应用融冰技术除冰时，分裂导线的各子导线并不是同时脱冰的，而是一根子导线首先脱冰，在该子导线覆冰脱落过程中将产生振荡冲击波，通过间隔棒传递到与之相连的其他子导线，使其他子导线在冲击力、覆冰重力和风荷载的综合作用下，发生覆冰脱落。现场融冰试验的观测也验证了这个现象[13]。文献[4,6]对此现象进行了简化研究，即只考虑覆冰质量，对单子导线发生脱冰引发分裂导线的整体扭转和跳跃进行了研究，但没有考虑此过程中引发的覆冰脱落。本节在考虑覆冰刚度的前提下，研究分裂导线中单根子导线发生覆冰脱落引起的连锁反应。通过杀死分裂导线中的某根子导线的全部覆冰，模拟该子导线的覆冰脱落过程，同时研究分裂导线中其他子导线的脱冰率和跳跃高度，分析其影响因素。

3.1 分裂导线单子导线脱冰过程

从表2的工况1可知，当跨度为200 m时，4分裂导线的单子导线脱冰将引起分裂导线的完全脱冰。从图9可以看到分裂导线的脱冰过程。为了方便观察，导线的变形放大了10倍。4号子导线脱冰发生0.5 s后，发生跳跃，带动分裂导线整体扭转跳跃，1—3号导线的脱冰过程尚未开始；脱冰发生后1 s时，3号子导线发生脱冰，2号子导线两端开始脱冰；1.5 s后，2号子导线发生脱冰，1号子导线未脱冰；2 s后，分裂导线完成脱冰，脱冰率100%。这是因为4号子导线发生脱冰后，其弹性势能转化为动能，向上跳跃，通过间隔棒的连接，对3号子导线的冲击作用最大，故3号子导线最先脱冰；3号子导线脱冰的过程中，也会产生新的动能，与4号子导线脱冰产生的动能一起使2号子导线脱冰，最后1号子导线发生脱冰。由此可见当跨度较大时，单子导线脱冰能够引起分裂导线的整体脱冰，这与在融冰观测中，单子导线脱冰能够加速分裂导线脱冰过程的现象是吻分别建合的[13]。

图8 冲击力与跳跃高度的关系Fig.8 Relationship between shock-load and jump height

图9 脱冰过程Fig.9 Process of ice-shedding

3.2 分裂数对脱冰率的影响

立跨度为100 m的水平二分裂导线、竖向二分裂导线、三分裂导线和四分裂导线的有限元模型，各子导线的位置分布见图1。表2列出了各脱冰工况参数及相应的模拟结果。从工况1—4可知，水平二分裂的1号子导线脱冰率为57.6%；竖向二分裂导线1号子导线的脱冰率为100%；三分裂导线1号和3号子导线的脱冰率分别为41.2%和44.8%；四分裂导线的1—3号脱冰率分别为22.8%，34%和61.6%。可见，分裂导线中单子导线脱冰对不同分裂数，不同位置的子导线影响不同。二分裂导线水平分布和竖向分布的脱冰率相差很大。这是因为脱冰子导线向上跳跃，对正上方子导线的冲击作用最大，对水平方向的冲击作用较小。同理，四分裂导线4号子导线脱冰，3号子导线的脱冰率要比1、2号子导线的脱冰率大得多。同时也可以看出，分裂数越多，对脱冰子导线的约束越大，相同位置子导线的脱冰率越低。

3.3 风和气动力阻尼的影响

从表2可知:工况5中，4号子导线脱冰，考虑风荷载和气动力阻尼，1—3号子导线脱冰率分别为22.8%，34%和61.6%；工况6中，考虑风荷载而不考虑气动力阻尼，1—3号子导线的脱冰率分别为22.8%，34%和61.6%,脱冰率没有变化；工况7中，不考虑风荷载和气动力阻尼，1—3号子导线的脱冰率分别为20.8%，30.8%和64.4%，1—2号子导线脱冰率都减小了10%，3号子导线脱冰率增大了5%。由上可知，跨度为100 m的四分裂导线气动力阻尼对脱冰的影响较小，可忽略不计；风荷载的影响相对较大，应予以考虑。这是因为风荷载作用在覆冰导线和裸导线上的力不同，会引起分裂导线扭转振动。如图10所示，四分裂导线的2号子导线和4号子导线是对称分布的，在无风的情况下，2号子导线和4号子导线脱冰造成的振荡是对称的，结果如表2中工况7—8所示。但考虑风荷载时，二者的反应并不相同。如工况5和工况10所示：前者引起的1号、2号和3号子导线的脱冰率分别为22.8%，34.0%和61.6%；后者引起的1号、3号和4号子导线的脱冰率为74.8%、36.4%和37%。由此可见，考虑风荷载的分裂导线脱冰与不考虑风荷载时，有一定差别，为了更准确地模拟分裂导线脱冰过程，应该在模拟中考虑风荷载的影响,气动力阻尼在跨度较小时可忽略。根据工况1可知，跨度较大时，单子导线脱冰引起的振动能够造成所有子导线脱冰，故没有研究风荷载和阻尼在跨度较大时的影响。

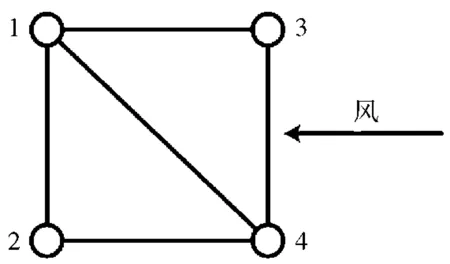
图10 四分裂导线受风荷载示意图Fig.10 Sketch of wind load on quad bundle conductor

3.4 间隔棒布置的影响

工况5布置了3组间隔棒，各次档距为24 m-30 m-26 m-20 m；工况9布置了2组间隔棒，各次档距为24 m-56 m-20 m。4号子导线脱冰时，工况5的1—3号子导线脱冰率均大于工况9的，这是因为脱冰导线的冲击作用通过间隔棒传递给1—3号子导线，传递点附近的覆冰受冲击作用发生脱落，3组间隔棒使冲击作用能够更好地传递，2组间隔棒情况下，1—3号子导线的跨中没有受到冲击，同时另2个冲击点也很难影响到跨中，因此脱冰率较低。图11给出了工况5和工况9中4号子导线(即脱冰子导线)的跳跃高度，可以看到导线中点附近没有间隔棒时，跳跃高度明显大于有间隔棒的情况。这样很容易与上方的3号子导线发生碰撞，引发事故。故实际中对分裂导线应该在档距中部附近布置一个间隔棒，能够有效抑制覆冰脱落的最大跳跃高度，对于导线的安全运行具有现实意义。

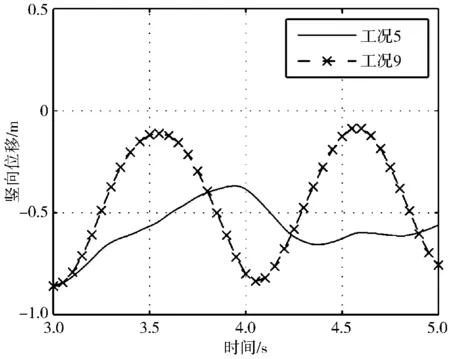
图11 4号子导线中点竖向位移Fig.11 Vertical displacement of middle point of subconductor 4

3.5 初始水平张力的影响

初始水平张力能够影响导线的初始刚度和初始形状，是输电线路的重要参数。考虑冰刚度时，覆冰会随着振动发生脱落。图12给出了四分裂导线子导线脱冰率随张力的变化关系，可以看出随着初始水平张力的增大，1—3号子导线的脱冰率随之减小。

图12 脱冰率与张力的关系Fig.12 Relationship between initial tension and ice-shedding rate

图13给出了各子导线最大跳跃高度与张力的关系，并与未考虑冰刚度的情况进行对比。可以看到，1—2号子导线的跳跃高度小于未考虑覆冰刚度时的跳跃高度，3—4号子导线的跳跃高度大于未考虑覆冰刚度时的跳跃高度。这是由于1—2号子导线的脱冰率很小，且冰刚度会抑制导线的运动，与未考虑冰刚度时相比，重量变化不大，但刚度大于后者，故1—2号子导线的中点跳跃高度小于未考虑冰刚度时的。对于3号子导线，脱冰率较大，虽然覆冰增加了导线的刚度，但随着脱冰的振动，覆冰逐渐脱落，导线的弹性势能转化为动能，其贡献大于该子导线剩余覆冰的刚度对导线的抑制作用，故跳跃高度大于未考虑冰刚度时的。4号子导线的跳跃高度大于未考虑冰刚度时的，这是因为1—3号子导线的脱冰，对4号子导线的抑制作用减弱，故跳跃高度较大。分裂导线的最大跳跃高度是脱冰子导线的最大跳跃高度，即图13中的4号子导线的最大跳跃高度。从上述分析可知，为了准确地模拟分裂导线覆冰脱落过程，在有限元模拟中应考虑覆冰刚度的影响，否则对跳跃高度的估计可能不安全。

图13 跳跃高度与张力的关系Fig.13 Relationship between initial tension and jump height

4 结 论

(1)对受冲击荷载作用的单导线覆冰脱落，风荷载的影响随着跨度和风速的增大而增大，故跨度较大时应考虑风荷载的影响；气动力阻尼在跨度较大时有一定影响，但脱冰运动较剧烈时，影响变小。对分裂导线单子导线脱冰，应该考虑风荷载的影响，跨度较小时可忽略气动力阻尼的影响。

(2)受冲击荷载作用的单导线覆冰脱落，脱冰率和跳跃高度与冲击荷载大小有关。

(3)分裂导线单子导线脱冰造成振荡，能够加速分裂导线的脱冰过程。

(4)分裂数和子导线的分布对分裂导线的脱冰率有一定影响。分布在脱冰导线正上方的子导线脱冰率最大，相同位置的子导线脱冰率随着分裂数的减小而增大。

(5)间隔棒的数目和分布会影响脱冰率和最大跳跃高度，在档距中部附近设置间隔棒，可以有效抑制脱冰跳跃高度。

(6)考虑覆冰刚度的分裂导线脱冰，能够模拟在脱冰振动过程中覆冰的破碎脱落过程，更符合实际情况，其最大跳跃高度大于不考虑覆冰刚度时的，故在脱冰过程中应考虑覆冰刚度，否则结果偏于不安全。

[1]王昕，楼文娟. 输电线路脱冰动力响应研究[J]. 工程力学, 2011, 28(1): 226-231. WANG Xin, LOU Wenjuan . Dynamic response analysis of multi-span transmission line to ice-shedding shock [J]. Engineering Mechanics, 2011, 28(1): 226-231.

[2]陈勇, 胡伟, 王黎明，等 . 覆冰导线脱冰跳跃特性研究[J]. 中国电机工程学报, 2009, 29(28): 115-121. CHEN Yong, HU Wei, WANG Liming, et al .Research on ice-shedding characteristic of icing conductor[J]. Proceeding of the CSEE, 2009, 29(28): 115-121.

[3]FEKR M R, MCCLURE G .Numerical modeling of the dynamic response of ice-shedding on electrical transmission lines[J]. Atmospheric Research, 1998,46(1): 1-11.

[4]严波, 郭月明, 陈科全,等 . 架空输电线脱冰跳跃高度的计算公式[J].重庆大学学报, 2009, 32(11) : 1306-1310. YAN Bo, GUO Yueming, CHEN Kequan, et al. Formula for jump height of overhead transmission lines after ice-shedding[J]. Journal of Chongqing University, 2009, 36(1) :1306-1310.

[5]沈国辉, 徐亮, 徐晓斌, 等 . 分裂导线-间隔棒体系的覆冰脱落研究[J].电网技术, 2012, 32(11): 201-206. SHEN Guohui, XU Liang, XU Xiaobin, et al .Research on ice-shedding of bundle conductor-spacers system[J]. Power System Technology, 2012, 32(11) : 201-206.

[6]KOLLAR E, FARZANEH M. Vibration of bundled conductors following ice shedding[J]. IEEE Transactions on Power Delivery, 2008,23(2) : 1097-1104. [7]KOLLAR E, FARZANEH M. Modeling sudden ice shedding from conductor bundles[J]. IEEE Transactions on Power Delivery, 2013,28(2) : 604-611.

[8]KALMAN T, FARZANEH M , MCCLURE G. Numerical analysis of the dynamic effects of shock-load- induced ice shedding on overhead ground wires [J]. Computers and Structures,2007,85(7-8) : 375-384.

[9]陈科全, 严波, 张宏雁, 等 . 冲击荷载下导线覆冰脱落过程的数值模拟[J]. 应用力学学报, 2010, 27(4): 761-766. CHEN Kequan, YAN Bo, ZHANG Hongyan, et al. Numerical simulation of de-icing on transmission lines under shock load[J]. Chinese Journal of Applied Mechanics, 2010, 27(4): 761-766.

[10]严波, 陈科全, 祖正华, 等 . 覆冰四分裂导线除冰过程模拟研究[J]. 振动与冲击, 2011, 30(11): 101-105. YAN Bo, CHEN Kequan, ZU Zhenghua ,et al. Numerical simulation study on de-icing process of iced quad-boundled conductor[J]. Journal of Vibration and Stock, 2011, 30(11): 101-105.

[11]陈科全, 严波,刘小会, 等. 覆冰导线机械式冲击除冰模拟研究[J]. 振动与冲击, 2012, 31(17): 129-133. CHEN Kequan, YAN Bo, LIU Xiaohui, et al. Numerical simulation of mechanical de-icing for iced transmission lines[J]. Journal of Vibration and Stock, 2012, 31(17): 129-133

[12]陈科全, 严波,吕欣, 等 . 四分裂导线机械式除冰装置及可行性研究[J]. 振动与冲击, 2013, 32(20): 48-54. CHEN Kequan, YAN Bo, LV Xin, et al .A mechanical de-icing device for iced quad-bundled conductors and its feasibility[J].Journal of Vibration and Stock, 2013, 32(20): 48-54.

[13]张志劲, 蒋兴梁,孙才新, 等 . 四分裂导线运行电流分组融冰方法与现场试验 [J]. 电网技术, 2012, 36(7): 54-59. ZHANG Zhijin, JIANG Xingliang, SUN Caixin, et al .De-icing method and field test of four-bundled conductor by loading operating current on grouped sub -conductors[J] .Power System Technology, 2012, 36(7): 54-59.

[14]蒋兴良, 易辉. 输电线路覆冰及防护[M].北京: 中国电力出版社, 2002: 32-57.

[15]张殿生. 电力工程高压送电线路设计手册[M].北京: 中国电力出版社, 2003: 175.

[16]蔡萌琦 . 分裂导线气动特性及次档距振动研究[D]. 重庆：重庆大学, 2014. CAI Mengqi. Investigation on aerodynamic characteristics and sub-span galloping of bundle conductors[D]. Chongqing: Chongqing University, 2014.

(编辑 张小飞)

Ice-Shedding Factors of Transmission Line

LI Jiaxiang， LI Hongnan，FU Xing

(Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, Liaoning Province, China)

Ice shedding, which can cause wire breaking, hardwire failure and flashover, is one of the common disasters for transmission line. In order to study the vibration mechanism of ice shedding, this paper constructs the model of transmission in the finite element software ANSYS, which considers the stiffness of ice and simulates two typical forms of ice-shedding with using the element birth and death method, including the shock-load-induced ice-shedding of a single conductor and one subconductor ice-shedding from bundle conductors. Then, we study the influences of line parameters and external load on the ice shedding through numerical simulation. The results show that: (1) during the shock-load-induced ice shedding, the influences of wind loads should be considered when the span is large; (2) the ice shedding rate and jump height increase with the increase of shock loads; (3) during the one subconductor ice shedding from bundle conductors, the vibration of one subconductor can accelerate the process of ice shedding of the whole span, so the wind loads should be considered; (4) the number and distribution of subconductors have influences on ice-shedding rate; (5) arranging a spacer near the middle of the span will reduce the jump height; (6) the simulation results will not be safe without considering the stiffness of ice. The research results can provide reference for the design of transmission lines.

ice shedding; stiffness of ice; ice shedding rate; jump height

国家自然科学基金委创新研究群体基金(51421064)

TM 726

A

1000-7229(2016)04-0076-08

10.3969/j.issn.1000-7229.2016.04.012

2015-12-22

李嘉祥(1985)，男，博士研究生，主要从事输电塔抗风和导线舞动研究；

李宏男(1957)，男，通讯作者，博士，教授，博士生导师，主要从事多维地震动，结构控制，大跨度输电塔结构的研究；

付兴(1988)，男，博士研究生，主要从事大跨高耸结构抗风(雨)振分析。

Project supported by Science Fund for Creative Research Groups of the National Natural Science Foundation of China(51421064)