计及弃风成本的含抽水蓄能电力系统随机优化调度

郭永明, 刘观起

(华北电力大学电气与电子工程学院，河北省保定市 071003)

计及弃风成本的含抽水蓄能电力系统随机优化调度

郭永明, 刘观起

(华北电力大学电气与电子工程学院，河北省保定市 071003)

针对风电入网的消纳难题，提出了抽水蓄能参与调峰的数学模型。将弃风成本作为经济指标之一，风速和负荷作为不确定变量，建立了风电-火电-抽水蓄能随机规划模型。处理机会约束条件时，提出以bootstrap抽样法估计置信区间，以提高精确度。在IEEE 30节点系统上进行仿真测试，对不同风电和抽水蓄能装机容量情况下的经济性进行分析。结果显示：风电装机容量由300 MW增加到400 MW时，弃风成本升高，系统对抽水蓄能的容量和备用容量需求也随之增加；当风电装机容量达到400 MW时，将抽水蓄能容量提高到90 MW，相比于无抽水蓄能参与调度的情况，能够节约经济成本约5%左右，且参与启停调峰的火电机组由2台减少到1台。算例表明针对不同装机容量的风电，合理地配置抽水蓄能容量，多元协调配合进行调峰，才能实现低成本消纳风电的目的。

弃风成本；抽水蓄能；随机规划；bootstrap抽样

0 引 言

随着化石燃料的逐渐枯竭，可再生能源发电的比例逐渐攀升，我国西北地区风电平均装机容量比例已达到25%以上，预计到2020年，我国的风电总装机容量将突破200 GW。然而，风速的预测难度较大，其随机性、间歇性和波动性导致预测精度低[1]，加之负荷低谷时，风电的反调峰特性增强[2-3]，致使风电消纳的难题日趋明显。大规模的风电入网后，若无相应的储能策略，会使大规模火电机组频繁启停，严重影响系统运行的经济性。抽水蓄能(pumped storage, PS)[4]作为储能方式中最经济可靠的手段之一，起到时间上转移风能的作用，能够缓解风电入网后造成的压力。

目前，很多文献对风电、火电、抽水蓄能的联合运行进行了相应的研究。文献[5]建立了风电-火电-抽水蓄能联合经济调度模型，以随机规划的思想，对机组组合和抽水蓄能出力进行了优化。文献[6]进一步考虑了电能质量约束条件，提出了一种新的风电-抽水蓄能联合经济运行策略。文献[7]以弃风量最小为目标，协调风电与抽水蓄能的出力进行调峰，以达到消纳风电的目的。诸如此类研究多从最大化消纳风电的角度出发，优化抽水蓄能和火电机组组合，而对不同的调峰需求下，抽水蓄能参与调度的经济性研究尚不够细致，考虑的约束尚不够全面。

本文将弃风成本作为经济指标之一，考虑风速和负荷的不确定性，采用bootstrap法估计置信区间，优化备用容量，以随机规划方法进一步完善风电-火电-抽水蓄能联合运行的模型。在IEEE 30节点系统上进行测试，分析抽水蓄能参与调峰的经济性。

1 联合系统的数学模型

1.1 运行成本

风电-火电-抽水蓄能系统的运行成本主要包括三方面，即弃风成本、火电机组运行成本、抽水蓄能运行成本。

引入弃风惩罚因子CW，弃风成本F1可表示为

(1)

(2)

(3)

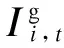
1.2 机会约束条件

以预测期望与误差值的和的形式表示风速和负荷的真实值：

vt=vft+et

(4)

PLt=PfLt+eLt

(5)

式中：vft和PfLt为预测期望；et和eLt为误差。

风电功率可表示为

(6)

式中：vin、vN、vout、v分别为切入风速、额定风速、切出风速、实际风速；PWN为装机容量[8]。

考虑风速和负荷预测的不确定性，以机会约束表示旋转备用容量需求和潮流限制，即：

(7)

(8)

式中：η为置信水平；h(PLt)和h(PWt)分别为负荷和风电随机样本。

购买负荷和风电的旋转备用容量需要满足短时间爬坡约束[9]：

(9)

根据控制性能标准(controlperformancestandard，CPS)[10]，自动发电控制(automaticgenerationcontrol，AGC)在5min内使控制偏差降到0，因此，T1=5min。其中：rup,i，rdown,i为爬坡速率，若考虑事故备用的爬坡限制，需要增加如下约束[11]：

(10)

同理，根据GPS标准，事故备用需在15min内补偿损失的发电容量，因此T2=15min。事故备用总容量以大于最大负荷的10%为宜。

以机会约束条件表示潮流限制：

(11)

(12)

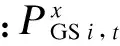
1.3 抽水蓄能相关约束

抽水蓄能以发电状态运行时，爬坡速率快，功率连续可调；以抽水状态运行时，功率固定或在几个离散值上可调[12]。

抽水和发电两种状态下需满足：

(13)

(14)

(15)

式(15)表示抽水和发电状态不能同时进行。调度初始的水库水量应在一定范围内平衡，以上水库为基准，可表示为

(16)

此外，水库水位不能超过规定的上下限，具体内容见文献[13]。

1.4 火电机组相关约束

火电机组相关约束主要包括功率平衡、可调出力极限等约束：

(17)

(18)

本文调度时间间隔为60 min，因此，T60=60 min。PGi,max和PGi,min分别为火电机组最大和最小功率极限。此外，还应兼顾机组的最小连续运行和停运时间。

2 机会约束的转化及模型求解

2.1 置信区间的估计

在转化机会约束条件时，需要将随机变量和确定变量分离，表示为如下形式：

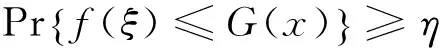
(19)

式中：ξ为随机变量；x为确定变量。h(ξ)为随机样本，本文提出以bootstrap重抽样法处理机会约束条件，具体流程见图1。

采用Monte Carlo模拟[14-15]进行大数抽样，样本选取不恰当时易造成较大误差。bootstrap方法[16]相当于多次重复的Monte Carlo抽样，可以设定较小的方差阈值，对置信区间的估计结果进行筛选，在多次大数定律的保证下，降低了坏结果的发生概率，误差较小。

图1 置信区间估计流程Fig.1 Process of confidence interval estimation

2.2 模型求解

以总成本最小为目标进行优化，即：

minF′=min(F1+F2+F3)

(20)

处理机会约束条件后，以成熟的数学规划软件进行求解。决策机组重新启动时，数学规划软件主要以该时刻的启停成本为基准，可能造成煤耗成本较高的机组先启动，若运行时段较长，则导致成本增加。因此，需要进行校验和修正：

(1)为了承担部分备用容量，重新启动的机组为Gk1、Gk2……Gkn。

(2)根据Gk1～Gkn煤耗成本曲线的“高低”，从低到高排序。

(3)以新的排序结果来决策火电机组在时间上的启动顺序，与原始方案对比，选出经济成本较低的方案。

一般地，以新的排序结果修正启动顺序的方案经济成本较低。

3 算例分析

3.1 算例系统

本文采用文献[9]中的IEEE 30节点系统，抽水蓄能电站由2台可逆式机组构成，最大发电功率分别为60 MW和30 MW；抽水时功率固定为最大值。各机组的布局如图2所示。火电和抽水蓄能机组参数。其中，G3为启停调峰机组。置信水平95%，线路潮流上限350 MW。根据风电上网电价，弃风惩罚100 美元/( MW·h)，负荷和风速预测，误差分别为2%和5%～16.5%线性递增。vin、vN、vout分别为3.5、13.5、25 m/s。

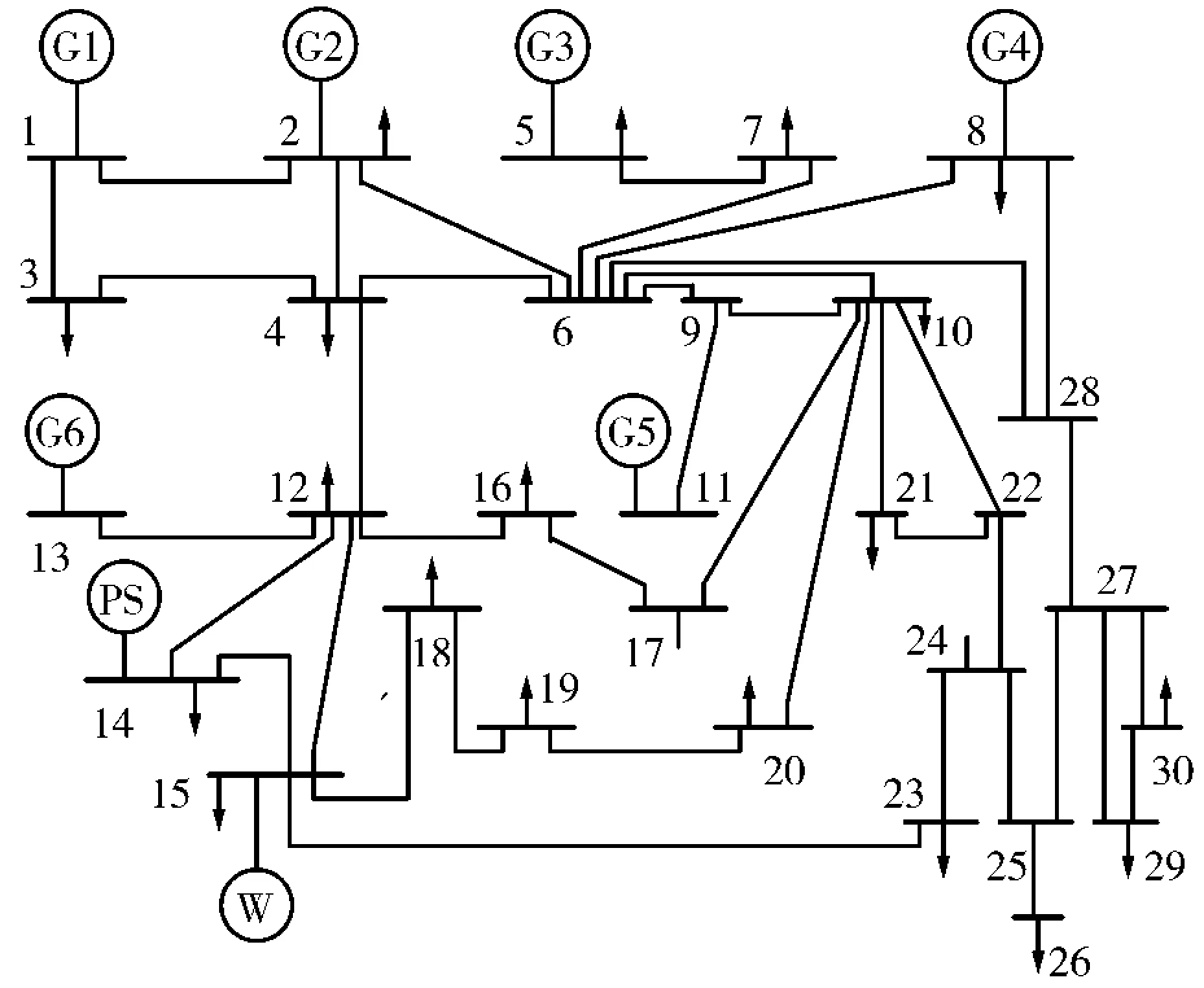
图2 IEEE 30节点系统布局Fig.2 Layout of IEEE 30-bus system

3.2 经济成本分析

以风机装机容量分别为300、350、400 MW，抽水蓄能为M1(不运行)、M2(运行1台60 MW)、M3(运行2台，30 MW+60 MW)3种模式，经济成本分析如表1所示。

表1 风电-火电-抽水蓄能联合系统成本分析
Table 1 Cost analysis of wind power-thermal power-
pumped storage combined system

由表1可知，随着风电装机容量增加，为了保证系统的可靠性，购买的备用容量增大，致使备用成本上升，加之弃风加剧，造成总经济成本的水平上升，抽水蓄能主要降低了弃风成本，不同模式下各时段弃风量如图3所示。

当风电装机容量为300 MW时，抽水蓄能投入运行，总成本反而增加。主要由于风电装机容量较小，尚无需抽水蓄能进行调峰，关停发电成本高的G3即可达到调峰的目的。若此时配置抽水蓄能参与调峰，则发电成本较高的G3保持发电状态，虽然能消纳风电，但长时间开机会使经济成本上升。

风电装机容量增加到350 MW时，M2模式下1台60 MW抽蓄机组进行调峰即可消纳全部风电，如再增加抽水容量，以M3模式运行，G3仍开机运行，经济成本上升。

风机装机容量为400 MW时，调峰需求增加。2台抽蓄机组进行调峰，风电全部消纳，节约了约5%经济成本。

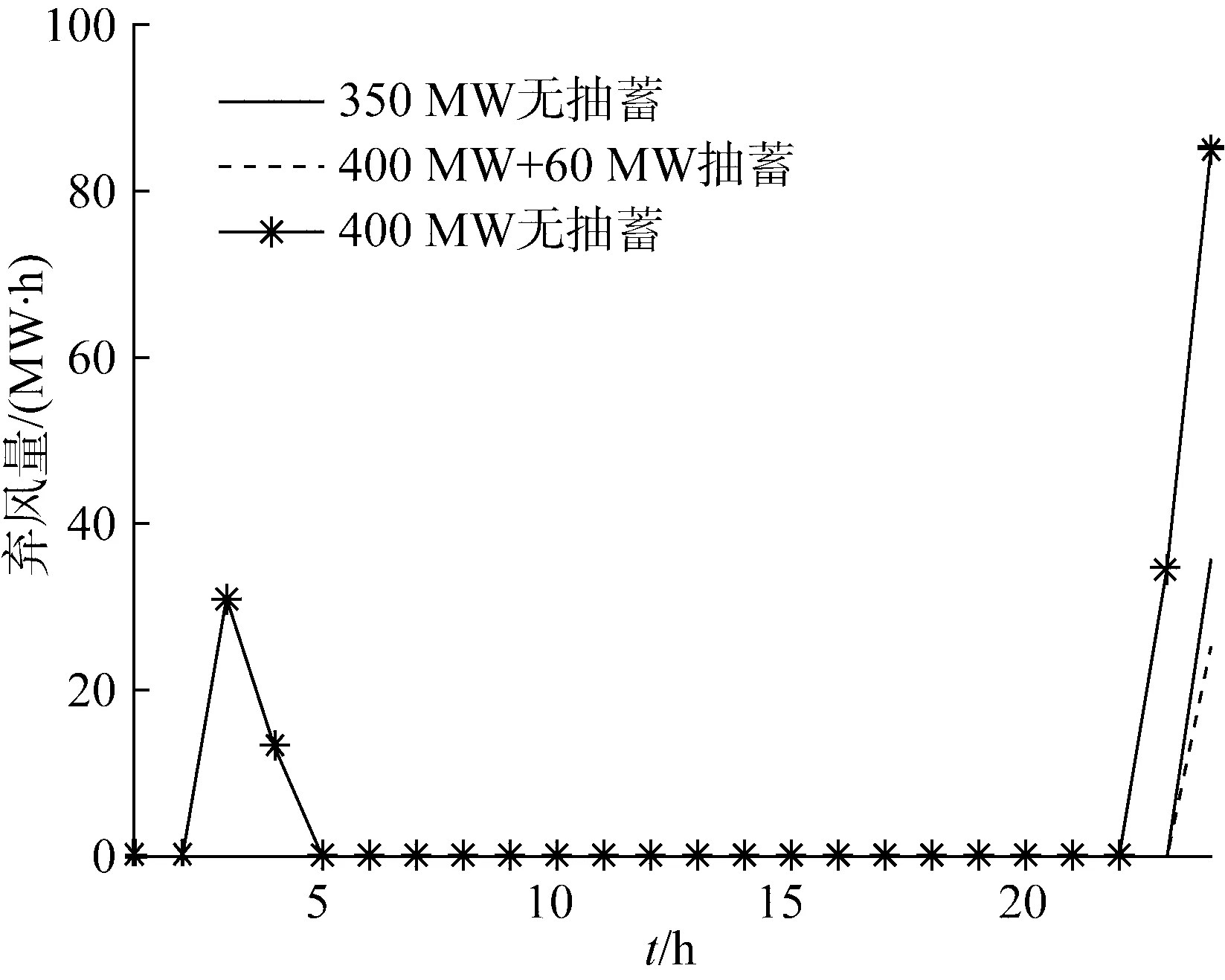
图3 各个调度时段的弃风量Fig.3 Wind curtailment in each scheduling period

3.3 机组组合结果

以风电装机容量400 MW为例，火电机组组合结果和抽水蓄能电站功率分别如图4、5所示。

图4中M1和M2模式下，调度中后期为了满足5 min备用爬坡的约束(式(9))，2台机组G3和G6重新启动承担部分备用容量。决策机组重新启动时，修正前启停成本较低的G3先于G6启动，经过校验，G6率先启动的经济性较好。由于系统中只有G3启停调峰的经济性高于深度调峰，M3模式下，避免了G6参与启停调峰，减轻了火电机组的启停压力，且多数机组出力趋于平缓。当风电装机容量进一步增大时，若无抽水蓄能，参与启停的火电机组将增多。

图5显示了抽水蓄能的出力情况，正值为发电，负值为抽水。在负荷低谷时段抽水消纳风电；在峰荷时段发电保持水量平衡。

综合3.2和3.3的结果可知，当风电装机容量较小调峰需求不高时，无需配置抽水蓄能就可达到良好的调峰效果。当风机装机容量较大，调峰需求升高时，合理优化抽水蓄能参与调度，可减少参与启停的火电机组个数，经济性较好。

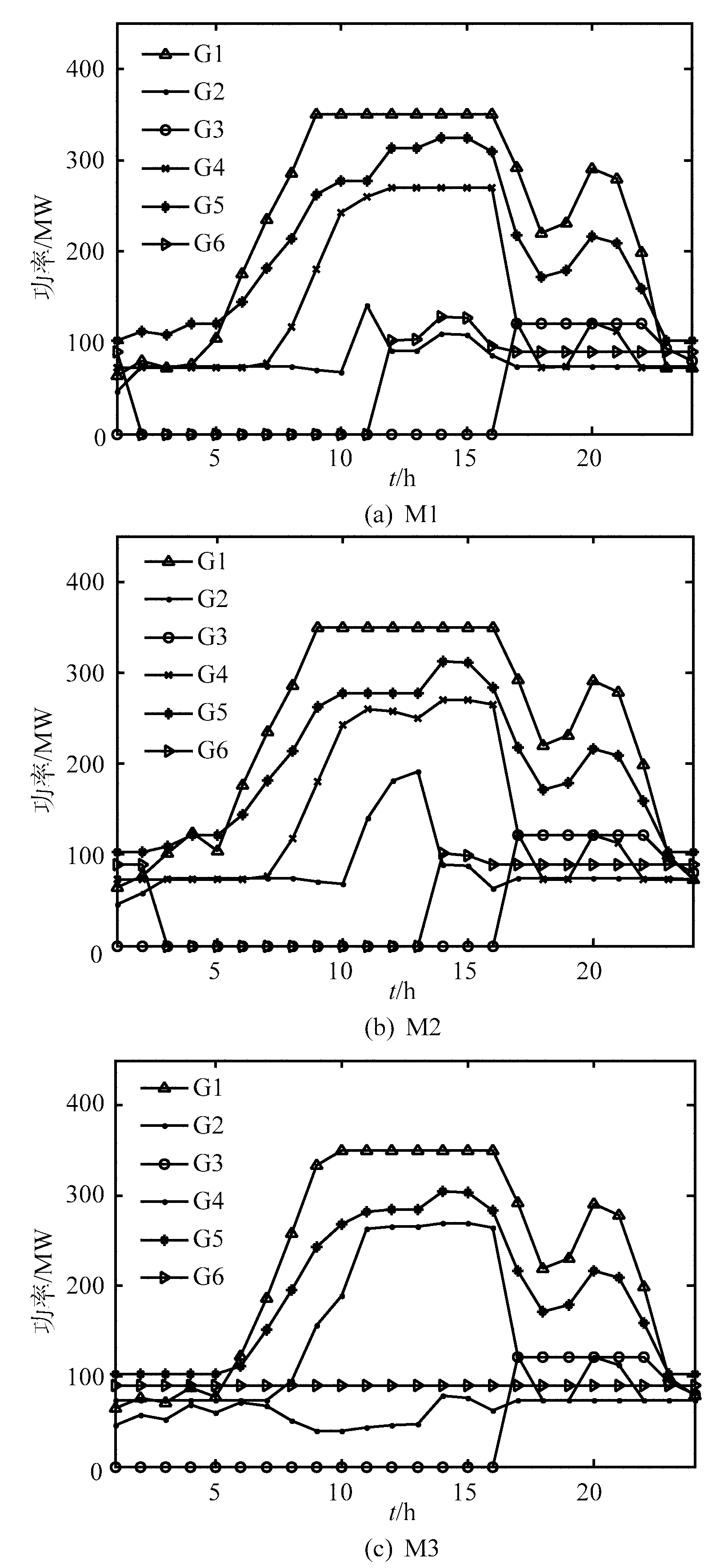
图4 火电机组组合结果Fig.4 Combination results of thermal power units

风电装机容量为400 MW时，随抽水蓄能容量逐渐增加，经济成本变化如图6所示。

由图6可知，随着抽水容量的增大，弃风现象逐渐消失。但抽水容量过大会使总经济成本上升，这主要是由于大功率抽水使煤耗成本高的小容量G3长时间开机。因此，抽水容量配置应不影响火电自身调峰能力。

4 结 论

(1)随着风电装机容量增大，备用成本和弃风成本上升是造成总成本上升的主要原因，抽水蓄能起到缓解系统的调峰压力的作用。

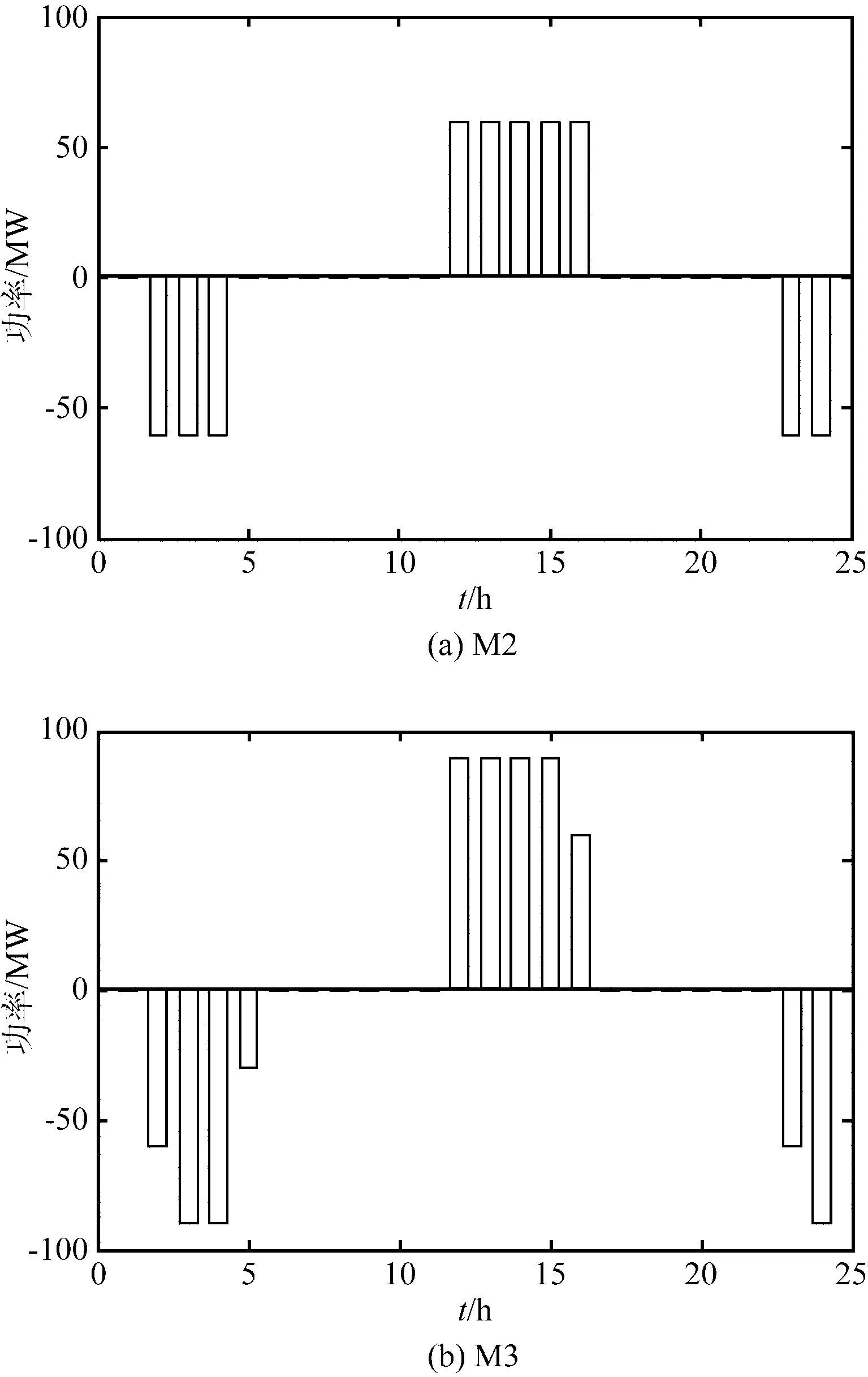
图5 抽水蓄能发电和抽水功率Fig.5 Generation power and pumping power of pumped storage

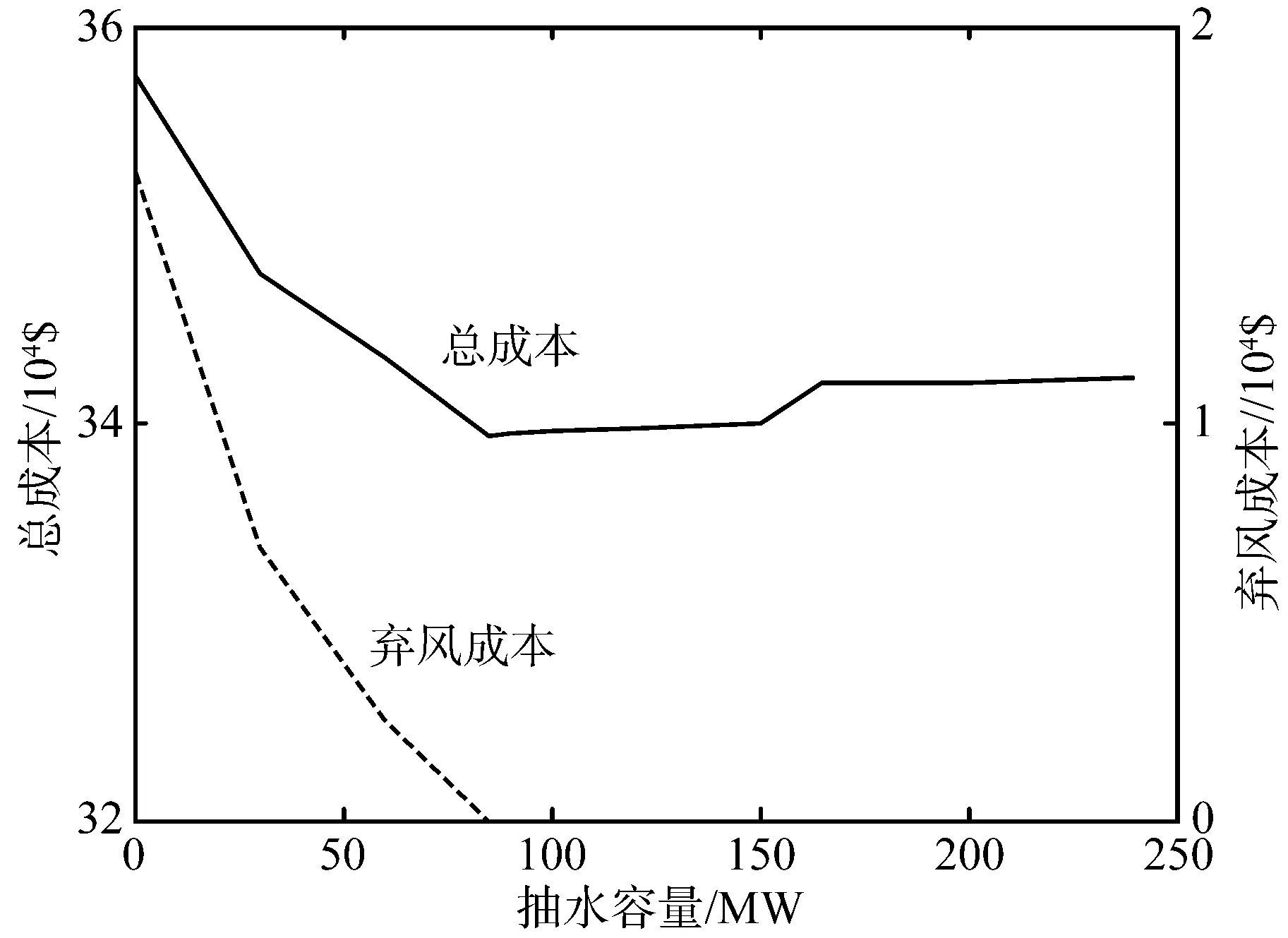
图6 经济成本随抽水容量的变化趋势Fig.6 Change trend of economic cost with pumped storage capacity

(2)不同装机容量的风电入网后，调峰需求会产生差异。抽水容量的配置应与系统调峰需求相适应才能达到良好的经济效果。

应当指出，本文是从某一置信水平的角度出发进行研究的。考虑不同置信水平进行优化求解分析将是进一步完善的内容。

[1]刘吉臻，王海东，李明扬.含风电的电力系统机组组合问题研究综述[J].电力建设，2014，35(12)：38-45. LIU Jizhen，WANG Haidong，LI Mingyang.Review on unit commitment of power systems with wind power integration [J].Electric Power Construction，2014，35(12)：38-45.

[2]郭飞，王智冬，王帅，等.我国风电消纳现状及输送方式[J].电力建设，2014，35(2)：18-22. GUO Fei，WANG Zhidong，WANG Shuai，et al.Consumption situation and transmission modes of wind power in China[J].Electric Power Construction，2014，35(2)：18-22.

[3]陈国恩，宗鹏鹏，朱伟，等.计及可再生能源与负荷互补特性的储能随机调度[J].电力建设，2015，36(6)：27-22. CHEN Guoen，ZONG Pengpeng，ZHU Wei，et al.Stochastic dispatching of energy storage devices considering complementarity between renewable energy and load [J].Electric Power Construction，2015，36(6)：27-22.

[4]BARTON J P，INFIELD D G.Energy storage and its use with intermittent renewable energy[J].IEEE Transaction on Energy Conversion，2004，19(2)：441-448.

[5]刘芳，潘毅，杨军峰，等.风电-火电-抽水蓄能联合优化机组组合模型[J].中国电机工程学报，2015，35(4)：766-775. LIU Fang，PAN Yi，YANG Junfeng，et al.Unit commitment model for combined optimization of wind power-thermal power-pumped storage hydro[J].Proceedings of the CSEE，2015，35(4)：766-775.

[6]王乐，周章，尉志勇，等.风电-抽水蓄能联合系统的优化运行研究[J].电网与清洁能源，2014，30(2)：70-75. WANG Le，ZHOU Zhang，WEI Zhiyong，et al.Research on optimal operation of hybrid wind power and pumped hydro storage system [J].Power System and Clean Energy，2014，30(2)：70-75.

[7]邹金，赖旭，汪宁渤.以减少电网弃风为目标的风电与抽水蓄能协调运行[J].电网技术，2015,39(9)：2472-2477. ZOU Jin，LAI Xu，WANG Ningbo.Mitigation of wind curtailment by coordinating with pumped storage[J].Power System Technology，2015，39(9)：2472-2477.

[8]吴义纯，丁明.基于蒙特卡罗仿真的风力发电系统可靠性评价[J].电力自动化设备，2004，24(12)：70-72. WU Yichun，DING Ming.Reliability assessment of wind power generation system based on Monte-Carlo simulation[J].Electric Power Automation Equipment，2004，24(12)：70-72.

[9]罗超，杨军，孙元章，等.考虑备用容量优化分配的含风电电力系统动态经济调度[J].中国电机工程学报，2014，34(34)：6109-6118. LUO Chao，YANG Jun，SUN Yuanzhang，et al.Dynamic economic dispatch of wind integrated power system considering optimal scheduling of reserve capacity[J].Proceedings of the CSEE， 2014，34(34)：6109-6118.

[10]国家电力监管委员会.电网企业全额收购可再生能源电量监管办法[Z].北京：国家电力监管委员会，2007.

[11]张国强，张伯明.考虑风电接入后二次备用需求的优化潮流算法[J].电力系统自动化，2009,33(8)：25-28. ZHANG Guoqiang，ZHANG Boming.Optimal power flow approach considering secondary reserve demand with wind power integration[J].Automation of Electric Power Systems，2009，33(8)：25-28.

[12]徐帆，刘军，张涛，等.考虑抽水蓄能机组的机组组合模型及求解[J].电力系统自动化，2012，36(12)：36-40. XU Fan，LIU Jun，ZHANG Tao， et al. Unit commitment problem with pumped-storage unit[J]. Automation of Electric Power Systems，2012，36(12)：36-40.

[13]胡泽春，丁华杰，孔涛.风电—抽水蓄能联合日运行优化调度模型[J].电力系统自动化，2012，36(2)：36-41. HU Zechun，DING Huajie，KONG Tao.A joint daily operational optimization model for wind power and pumped-storage plant[J]. Automation of Electric Power Systems，2012，36(2)：36-41.

[14]王俊，蔡兴国，季峰，等.考虑新能源发电不确定性的可用输电能力风险效益评估[J].电力系统自动化，2012，36(14)：108-112. WANG Jun，CAI Xingguo，JI Feng，et al.Evaluation of risk and benefit of ATC relating to uncertainty of renewable energy power generation[J].Automation of Electric Power Systems，2012，36(14)：108-112.

[15]艾欣，刘晓.基于需求响应的风电消纳机会约束模型研究[J].华北电力大学学报，2011,38(3)：18-22. AI Xin，LIU Xiao.Chance constrained model for wind power usage based on demand response[J].Journal of North China Electric Power University，2011,38(3)：18-22.

[16]BREIMAN L. Bagging predictors[J].Machine Learning，1996，24(2)：123-140.

(编辑 蒋毅恒)

Stochastic Optimization Scheduling Method for Pumped Storage Power System Considering Wind Curtailment Cost

GUO Yongming, LIU Guanqi

(School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, Hebei Province, China)

According to the problem of wind power absorption in grid, this paper proposes a mathematical model for pumped storage units participating in peak shaving. We construct a stochastic programming model of wind power-thermal power-pumped storage association system, which takes wind curtailment cost as one of the economic indicators and wind speed and load as uncertain variables. When dealing with the constraint condition of opportunity, we adopt bootstrap sampling to estimate confidence interval, in order to improve the accuracy. Finally, we carry out the simulation test on the IEEE 30-bus system to analyze the economical efficiency under the condition of different wind power and pumped storage capacity. The results show that with the rising of wind power installed capacity from 300 MW to 400 MW, wind curtailment cost increases and the demand of pumped storage capacity and reserve capacity also goes up. When the wind power installed capacity arrives at the level of 400 MW and pump storage capacity raises to 90 MW, the economic cost can be reduced by 5% compared with that in the case without pumped storage in scheduling. Meanwhile, the number of start-up (shut-down) thermal power units is reduced from 2 to 1. Example shows that according to the different wind power installed capacity, the rational allocation of pumped storage capacity and the coordinative peaking of multiple sources can achieve the purpose of the wind power absorption at the least cost.

wind curtailment cost; pumped storage; stochastic programming; bootstrap sampling

TM 732

A

1000-7229(2016)04-0029-06

10.3969/j.issn.1000-7229.2016.04.005

2015-11-18

郭永明(1990)，男，硕士研究生，研究方向为电力系统分析、运行与控制；

刘观起(1956)，男，副教授，硕士生导师，研究方向为电力系统分析、运行与控制等。