基于样本熵算法的早产儿败血症发病预测模型探索

张世翌，刘志伟，王翼，潘钢

基于样本熵算法的早产儿败血症发病预测模型探索

张世翌，刘志伟，王翼，潘钢

针对早产儿患败血症几率较高但传统诊断较为滞后，易造成永久神经损伤的问题，提出了基于样本熵算法的早产儿败血症发病预测模型。将样本熵算法应用于心率变异分析，并根据心率数据特点优化选择了算法参数；然后，分析了基于本算法得出的样本熵变化与新生儿败血症发病的关联性和预测作用。结果表明，模型对于早产儿败血症发病预测结果与实际病程相符，对进一步研究提供了方向。

新生儿败血症；预测模型；心率变异性分析；样本熵

0 引言

早产儿患败血症的几率较高，伴随着永久神经损伤的风险的同时，还有近20%的死亡率[1]，而传统的诊断往往是在患儿出现严重的症状之后才能确诊。如果能提早预测其发病并在临床症状出现之前就进行目标导向的治疗，将无疑大大提高存活率和治愈率。心率特性是重要的临床监护特征，国外研究显示，患儿心率在败血症发生前有变异性下降以及瞬时心跳减速的特性。预测监护即在败血症发病之前，对患儿心率进行持续监测，并通过计算模型对数据进行自动分析，预测发生败血症的几率[2]。

本文结合我国新生儿临床心电监护数据，对基于多参数融合的早产儿败血症发病预测模型进行研究。通过国际和平妇幼保健院新生儿重症监护室（Neonatal Intensive Care Unit，NICU）数据采集平台输出心率数据，并在此基础上设计基于样本熵算法的心率分析算法，配合临床诊断，评估样本熵变化与新生儿败血症发病的关联性，为以后在国内实现早产儿败血症全自动预测性监护系统奠基。

1 新生儿败血症发病预测模型

与新生儿败血症相关的影响因子包括胎龄、出生体重、年龄等，利用这些参数计算发病几率，我们称其为静态模型[2]。静态模型的准确度对原始数据有很强依赖，所以往往不能具有很好的普适性。为了克服静态模型的缺点，考虑利用心率变异、呼吸率和氧饱和等的特征来预测发病几率，则称为动态模型。国内对于基于动态模型的败血症预测研究进展很少，尤其是在研究心率变异的领域更几乎是空白。本文致力于搭建基于心率检测的新生儿败血症预测动态模型。

心率变异性（Heart Rate Variability，HRV）是指窦房结在自主神经调节下瞬时心率的微小涨落。中枢神经系统、呼吸活动以及由压力、化学感受器传入的心血管反射活动等均对其有影响[3,4]。在败血症血液培养确诊前24到前12小时，心率变异性降低，并且伴随着心率暂态减速，通过检测心率特性的改变能实时地预测败血症的发生。然而，虽然心率在ICU一直持续不断地被监测着，但即使暂态减速时，心率也没有低到足够触及心动过缓警报的地步，所以仅仅依赖绝对值阈值往往不能提供有效的诊断参考。为了反映心率变异的情况，目前已有的分析方向包括时域分析（SDNN、SDANN等）、频域分析（总功率、低频高频成分等）和散点图分析（Poincare散点图、Lag散点图等）[5]。而国外有研究显示，一些连续测量算法应用在心电信号评估上会有相对更好的效果，比如样本熵算法和样本非对称性算法[3]。

1.1 样本熵算法

生理信号蕴含的非线性复杂度信息的多少与生理系统的功能状态密切相关，而熵测度算法由于需要的数据量较少（只需约100到5000个数据即可得出稳定的熵值），在短时生理信号尤其是相对数量众多、采集方便的心率信号的非线性复杂度分析中，有很好的效果。熵的概念是定量说明信号中信息重复性，熵值大说明信号中随机性或不规则信息较明显 ，反之信号较规则。熵算法中，以Pincus提出的近似熵(Approximate Entropy，ApEn)应用最为广泛。而样本熵则是Richman等提出的一种新的旨在降低ApEn误差的时间序列复杂性测法，它比近似熵算法有更好的无偏性，计算时间更短，且很大程度上独立于数据记录的长度，结果保持相对的一致性[4]。简单描述样本熵，就是求一种条件概率——若两个窗宽为m的序列相似，则在容差r允许的范围内，在下一点依然相似的概率。具体算法描述如下：

（1）原时间序列抽取模板连续点：设时间序列X=｛x1,x2,…,xN｝，依次取于m个连续点组成矢量Ym(i)=｛xi,xi+1,…,xi+m-1｝,i=1～(N-m+1)，共有N-m+1个m维矢量。

（2）计算矢量间距离：定义矢量Ym(i)与Ym(j)之间的距离d［Ym(i),Ym(j)］=max(|xi+κ-xj+κ|)，其中k= 0～(m-1)，i,j=1～(N-m+1)，i≠j。

（3）设定容差阈值，r=HσX，其中σX为时间序列的标准差，H为增益因子。对于N-m+1个m维矢量，统计不包含元素Ym(i)在内的N-m个矢量中与元素Ym(i)的距离小于阈值r的元素数目，记为模板匹配数Nm(i)，并计算Nm(i)与距离总数N-m的比值，记为，对所有的i=1～(N-m+1)，求的均值，记为：

（4）将空间维数增加至m+1，依照上述步骤重新计算Bm+1(r)。

（5）则时间序列的样本熵为：

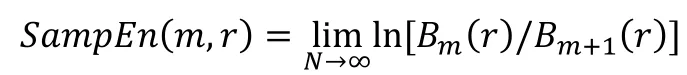
对于序列元素个数N为有限数的时间序列，按照上述步骤得到的样本熵为：

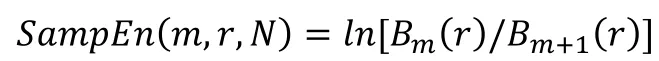
2.2 参数选择

对于心率数据，调用样本熵算法计算的结果在时间尺度上是较为密集而离散的数据，为了更直观地表现样本熵值的变化趋势，需要进一步平滑处理样本熵，用90%均线来反映以6小时为间隔的变化趋势。典型的样本熵、90%均线混合记录图如图1所示：

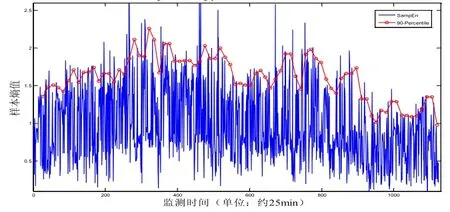
图1 样本熵（实线）和百分之九十均线（空心点连线）

其中实线表示样本熵SampEn，空心圆表示此前12小时的90%均值，即：将待统计样本熵由小到大排列，排在90%处的数值作为该值，每隔6小时统计一次，以形成90%均线。选取这个指标是因为，单纯的均值上下波动不明显，不能很好地对应病情变化，而它能反映前一段时间样本熵高值的变化趋势，经验证发现与病情密切相关；同时，90%极大值也避免了选取幅值波动剧烈、个别值过大的最大值而导致的过分灵敏。

尽管样本熵算法实现起来不算困难，但SampEn的值显然与抽取窗宽m和容差阈值r两个参数的取值有关。选取较小的m（短模板）和较大的r(宽容差)，可以让匹配结果数增加。但是，当r增加，匹配数将上升，SampEn将在各个点趋于0，这意味着序列的显著变化特征（如心率暂态减速尖峰）都可能识别不出来；而当m减小，那些不适合在精细尺度观察的特征（如大规模心率减速）也就会容易被忽略。基于这些原因，参数的具体取值还没有一个最佳确值，Richman的研究提供了一个优化的范围，对于100点到5000点长度之间的序列，r取0.1到0.25倍序列标准差，m取1或2[9]。考虑本文研究对象为间隔5s的心率数据，对一组数据做控制变量的参数调试。

在r=0.2*SD条件下，分别选取m=1,2,3,4，结果如图2所示：

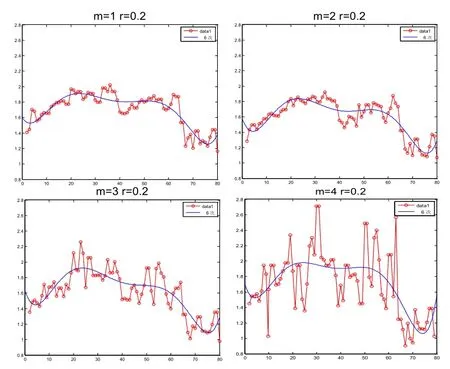
图2 r=0.2，m=1,2,3,4样本熵结果对比

m=1和2时，样本熵波动范围很小，而m=4时，样本熵波动范围太大。所以折衷选择m=3。

在m=3的条件下，分别选取r=(0.1,0.15,0.2,0.25)*SD，结果如图3所示：

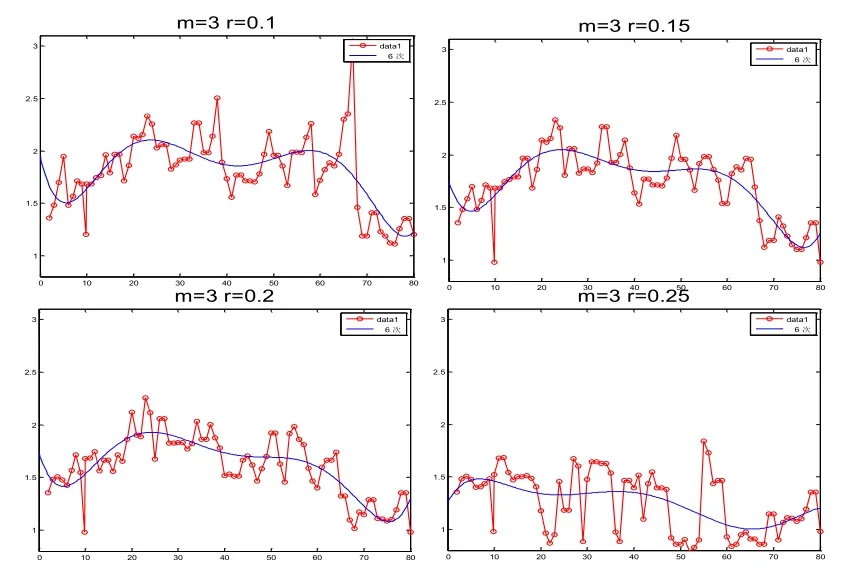
图3 m=3，r=0.1,0.15,0.2,0.25样本熵结果对比

r=0.1时，波动幅度较大，且有高峰毛刺，这对于研究下降趋势来说是很不利的。r=0.15时，波幅有所收敛，效果较好。r=0.2时，波幅进一步收敛，效果最好。r=0.25时，大量样本熵下探低处，大大削弱拟合曲线的下降趋势。所以选择r=0.2。

综上，参数m=3，r=0.2*SD，既能反映不同时间样本熵的波动，又能保证拟合曲线的趋势相对明显。

1.3 模型搭建

采集心率数据。选择在国际妇幼儿童保健院出生的合适对象，满足胎龄小于34周，或者体重小于1800克的条件，连续监测心率并记录。

对数据进行预处理。原始心率数据采集间隔为5秒，考虑分为300个点一组，以类比4096个RR间期（此处来源于文献），约25分钟。对于末尾不足300的，做补零处理。

调用样本熵计算程序对每一组求值。算法参数为m=3,r=0.2*SD。由于算法本身的特点，结果可能出现除无意义或者无穷大的值，需要剔除，剔除过后等效于数据缺失，有文献表明，缺失数据点对于样本熵变化趋势研究影响较小[6]。

计算90%均值，表征该点前六小时的样本熵变化情况。

对上述均值折线做高次多项式拟合，更加平滑直观的趋势线。根据90%均值在趋势线的上方或下方，预测判断发病情况。

2 数据分析

2.1 临床数据总结

根据上述研究对象选择标准，在NICU中选取了7位监护婴儿，进行 24 小时连续临床心率数据采集。他们胎龄从27周到33周，出生体重范围940克到1430克，在NICU治疗期间，1位婴儿确诊发生感染并死亡，3位确诊发生感染并治愈，3位婴儿未见感染。以下以3位患儿作例子详细分析。发生感染的1号患儿，5月19日发生感染，5月22日病情恶化，5月26日死亡。2号患儿，5月8日发生感染，5月9日用药治疗，5月16日好转后停用抗生素，恢复。3号健康。

2.2 模型预测结果分析

1）发病且恶化情况：

1号病人的心率变异计算模型结果如图4所示：

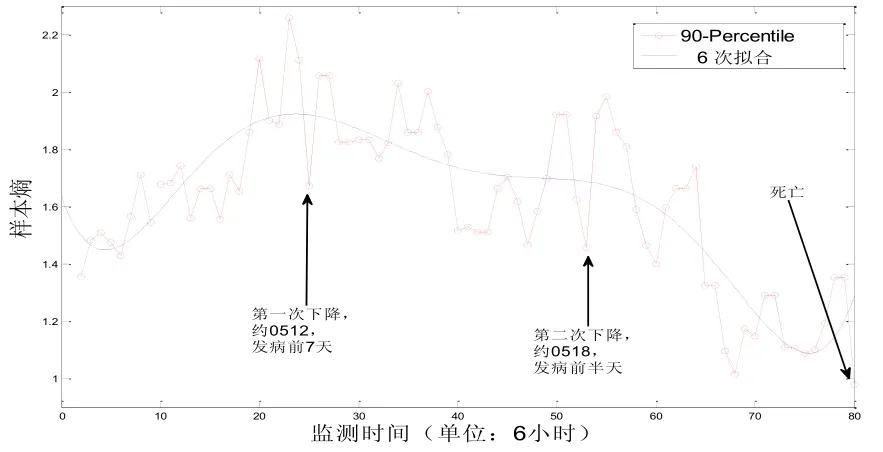
图4 1号病人样本熵模型（百分之九十均线和高次拟合曲线）计算结果

其中横坐标为心率监测的时间轴，对应开始监测后经过了多少个6小时。纵坐标则为对应的样本熵计算值的90%均值。观察曲线，坐标25处（对应5月12日，发病前7天）开始出现第一次下降，样本熵显著低于均线，此后均线一直持续下降。到坐标53（对应5月18日，发病前半天），第二次明显下降，样本熵显著低于均线，此后均线以更大幅度下滑。坐标75（对应5月25日，死亡前一天），样本熵跌至历史低点。直至坐标80（最终死亡），样本熵始终维持低位。综上，配合病情记录分析可知，从12日开始，到19日出现肺炎需要吸氧，再到心衰乃至26日死亡，样本熵持续降低，且每一波下降起始点与病情发展密切相关。

2）发病且好转情况：

2号病人的心率变异计算模型结果如图5所示：

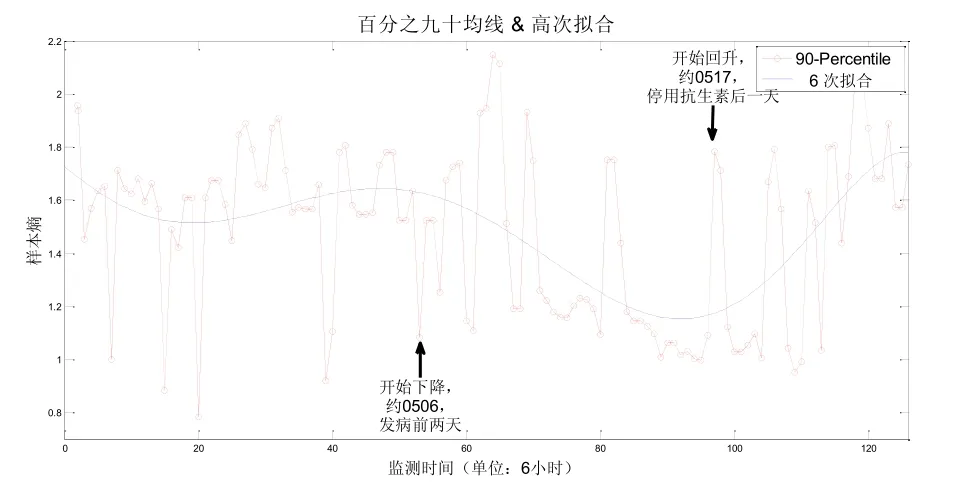
图5 2号病人样本熵模型（百分之九十均线和高次拟合曲线）计算结果

其中横坐标为心率监测的时间轴，对应开始监测后经过了多少个6小时。纵坐标则为对应的样本熵计算值的百分之九十均值。观察曲线，坐标55处（对应5月6日，发病前两天）开始下降，样本熵显著低于均线，此后均线一直持续下降。到坐标90（对应5月16日，停用抗生素），样本熵跌至历史低点。之后，坐标92（对应5月17日，停药后一天），样本熵重新猛升高于均线，且此后均线一直持续上升，直至恢复到略高于发病前值。坐标12（对应0516-0519）最低处后又猛烈反弹上升，直到坐标14（对应0522-0525）恢复甚至高于发病前值。综上，配合病情记录分析可知，样本熵5月6日提前发病两天展现下跌趋势后，8日出现腹隆症状，随病情发展样本熵持续降低，用药治疗期间样本熵值始终维持低位，直到16日停药好转之后，样本熵重新反弹上升，直至完全康复出院，整个变化过程与病情十分吻合。

3）完全正常情况：

3号病人的心率变异计算模型结果如图6所示：

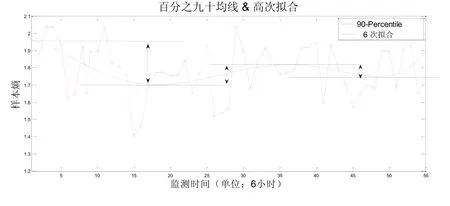
图6 3号病人样本熵模型（百分之九十均线和高次拟合曲线）计算结果

其中横坐标为心率监测的时间轴，对应开始监测后经过了多少个6小时。纵坐标则为对应的样本熵计算值的百分之九十均值。观察曲线，首先发现其绝对值波动范围较小（1.4-2.1，小于上两例0.8-2.2和0.9-2.2），其次从开始监测到结束，均线基本维持平稳，略有起伏但都不如上两例剧烈，且幅度逐步收窄。配合病情记录分析，该病人入住NICU后各项体征正常，没有发病或有明显发病征兆，样本熵亦平稳直至出院。

2.3 总结

根据上述典型病例分析发现，模型指标样本熵值的变化能反应新生儿败血症的发病以及病程变化情况。正常无病情况，样本熵保持稳定，波动有限。即将发病时，样本熵开始呈现骤降，随着病情发展，样本熵值会持续下降趋势并跌破低点。当药物干预治疗、病情缓和康复阶段，样本熵会回升。完全恢复正常后，样本熵亦恢复到发病前的值附近或略大。

3 总结

本文旨在研究NICU中临床心电监护数据对新生儿败血症的预测作用。本文通过合作单位国际和平妇幼保健院NICU数据采集平台输出心率数据，并在此基础上设计基于样本熵算法的心率处理及分析模型，配合临床诊断，评估模型的有效性，为以后在国内实现早产儿败血症全自动预测性监护系统提供理论基础。

[1] Fairchild K D. Predictive monitoring for early detection of sepsis in neonatal ICU patients.[J]. Current opinion in pediatrics, 2013, 25: 172-9.

[2] Clifford G D, Long W J, Moody G B. Robust parameter extraction for decision support using multimodal intensive care data.[J]. Philosophical Transactions. Series A, Mathematical, Physical, and Engineering Sciences, 2009, 411-429.

[3] Ahmad S, Ramsya T, Huebsch L. Continuous multi-parameter heart rate variability analysis heralds onset of sepsis in adults[J]. PLoS One, Public Library of Science, 2009, 4(8): e6642.

[4] Dick T E, Molkov Y I, Nieman G. Linking inflammation, cardiorespiratory variability, and neural control in acute inflammation via computational modeling[J]. Frontiers in Physiology, 2012, 3: 1-9.

[5] 彭秋莲, 卢广文, 李源等. 样本熵在预测阵发性房颤中的研究[J]. 中国医疗设备, 2008, 24(4): 2008-2010.

[6] 何欣. 脑电样本熵与双频指数评价丙泊酚靶控输注麻醉镇静深度的研究[D]. 天津医科大学, 2011.

Exploration on Predictive Model of Neonatal Sepsis Based on Sample Entropy Algorithm

Zhang Shiyi1, Liu Zhiwei2, Wang Yi2, Pan Gang1
(1. School of Biomedical Engineering, Shanghai Jiaotong University, Shanghai 200030, China; 2. The International Peace Maternity and Child Health Hospital of Shanghai, Shanghai 200030, China)

This article focuses on the prediction model of the incidence of sepsis in preterm children based on Sample Entropy algorithm, optimizes the chosen algorithm parameters, and analyses the relevance between the predict tive algorithm’s results and the neonatal sepsis onset.

Neonatal Sepsis; Predictive Model; Heart Rate Variability Analysis; Sample Entropy;

TP311

A

1007-757X(2016)10-0041-03

2015.12.20）

上海交通大学“医工交叉研究基金”（YG2013MS69）

张世翌（1992-），男，上海交通大学，生物医学工程学院，硕士研究生，研究方向：医学信号处理，上海 200030

刘志伟（1972-），上海国际和平妇幼保健院新生儿科，主任医师，研究方向：围产新生儿临床科研工作，上海，200030

王 翼（1983-），上海国际和平妇幼保健院新生儿科，主治医师，研究方向：围产新生儿临床科研工作，上海 200030

潘 钢（1956-），男，上海交通大学，生物医学工程学院，高级工程师，研究方向：医学仪器，上海 200030