快速实现三维可视化土石方量精确计算的方法与应用

左健扬, 倪万魁

(1.长安大学 地质工程与测绘学院, 陕西 西安 710054; 2.宁夏回族自治区 国土资源调查监测院, 宁夏 银川 750002)

快速实现三维可视化土石方量精确计算的方法与应用

左健扬1,2, 倪万魁1

(1.长安大学 地质工程与测绘学院, 陕西 西安 710054; 2.宁夏回族自治区 国土资源调查监测院, 宁夏 银川 750002)

[目的] 对快速实现三维可视化土石方量精确计算的方法与应用进行分析，为工程设计、决策安排提供有效参考依据。 [方法] 利用Petrel软件建立的数字高程模型，能够实现三维精准可视化土石方量的快速计算。 [结果] 通过模型精度评价认为，该方法不仅满足工程需要，模拟精度还要高于常用的Surfer软件。 [结论] 结合工程实例分析，采用该方法的土石方量精确计算不仅能够直观地展示工程预期成效，估算结果还更为保守可靠。

土石方量; 快速计算; 可视化; 精准化

土石方量计算在土木工程、水利水电和固体矿产采剥等诸多工程领域均有涉及，也是工程决策者所关心的问题，其计算成果不仅服务于工程实施的概预算，还会对工程总体设计、施工安排及进度有重要的影响。目前，土石方量计算的方法主要有等高线法、断面法、方格网法和数字高程模型方法(DEM)。前3种方法多采用手工计算，不仅效率较低且计算量很大，计算过程的准确性也难以得到有效保证。而DEM法提供对地形的精确数字描绘，结合计算机强大的运算能力,可以将传统的土石方计算方法与三维模型有效结合，使其成为快速、准确、可视化的工程量计算的有效途径。随着计算机应用技术的不断发展，基于DEM的三维可视化土石方量计算的快速精确化研究也在不断发展。目前土石方量可视化计算和精度分析多在不规则三角网和Surfer软件下进行，王京卫等[1]利用Surfer软件实现了施工场地的土石方量可视化计算，并对计算精度进行了分析整理；张勇等[2]通过Surfer下进行Kriging插值处理并在AutoCAD下实现3维实体建模可视化设计以及精度分析；陈丽华等[3]结合DEM技术利用二次曲面插值实现渣场三维显示及容积计算；孟永东等[4]利用分形布朗运动的插值算法实现TIN三角网模型下的方量计算和三维可视化分析；还有利用其他方法或模拟软件进行土石方量的可视化计算，如李洪涛等[5]利用ArcGIS实现填挖土石方量的可视化与土石方量调配最优化分析；冯晓刚等[6]探讨了三维激光扫描技术在土石方量精确计算中的应用。本研究利用Petrel三维地质建模软件，通过理论函数模型的建立与计算精度的分析验证，证明其具有很高的计算精度，完全能够满足工程应用。并结合工程实例，来对可视化模拟和方法实现进行探讨和研究。

1 土石方量计算的三维可视化方法

三维可视化方法不仅可以对事物进行直观的模拟描述，还可以帮助我们分析和研究模型问题。三维模型计算土石方量的实质就是利用空间离散数据点分别对施工前后的地表形态进行插值模拟，并通过三维空间上的曲面叠合，构建三维网格化数据实体模型。经过每个单元网格体积的累加计算得到模型体积，也就是地形变化空间差值模型体的体积。利用基于Windows系统的三维可视化建模软件Petrel对土石方量可视化及精度分析进行研究。

土石方量可视化模拟计算主要分为3个步骤： (1) 获取空间离散数据点以及工作区范围。根据实际工程的精度需要，获取相应的地形线拐点信息。可以通过矢量化地形图、纸质图件或野外实时测量，参数主要为平面直角坐标X，Y和高程Z。土石方量底面的确定可以根据实际需要(可以是水平面、斜面或者起伏变化的曲面)进行相应的确定。Petrel软件具有强大的数据处理能力，在对大量冗繁的数据点进行预处理时，不需要人为的精简数据，不仅极大的减少了人工筛余的工作量，也有效的保证了数据信息的完整性和真实性。 (2) 空间插值构建结构面。将预处理离散数据点文件通过对应项参数设置导入软件，空间数据点会自动在三维空间中生成并显示。通过在二维平面和三维空间视图下对数据点进行遗漏检查，并对数字化输入时的无效点直接修正(主要是删除非地形飞点数据或异常点查错更改)。选用合理的插值计算方法构建施工前后的网格曲面，网格划分越细，所表达的地形或地质现象精度相对越高，但软件模拟的运算处理速度也相对越慢。 (3) 建立三维实体模型。利用工作区范围拐点坐标作为模型边界，设定合理的三维网格密度，通过施工前后地形曲面的约束建立三维实体模型(bulk volume)，通过快速计算读取土石方量的体积。当对基岩面深度进行了有效控制(可通过钻孔、探槽等工程揭露获取)，通过分层模拟，还可以实现土方量和石方量的分别计算。

2 软件计算的精度分析

2.1 采样点密度的影响

计算精度是网格化模型模拟评价的重要指标，也是数字地形建模、数字地形分析和各种地学过程模拟最为关心的问题。对于不同插值方法及网格精度下的方量计算精度问题，王宝成，陈竹安等[7-8]对计算方法的精度分析做了一定的评价研究。为了便于对Petrel软件土石方量体积网格和计算精度进行定量分析，本研究参照文献[8]，利用函数理论模型的建立，来对网格化模型计算精度进行分析研究。

首先，在区域：D(0≤x≤100,0≤y≤100,z>0)上构建函数模型：

通过对理论函数模型做二重积分，获得模型的体积V，即

式中(x,y,z)空间向量的数值可以利用Excel进行计算得到。接下来分别从数据采样间隔和网格插值密度2个方面对模型精度进行分析。

(1) 在区域D内分别以5，10，20m共3种采样间隔采集离散数据点作为曲面构建网格化的源数据，并以1m×1m的网格密度利用克里金(kriging)插值方法对源数据进行曲面插值。

(2) 在区域D内以5m采样间隔采集数据点作为源数据，以1m×1m，2m×2m，5m×5m这3种网格密度下利用克里金插值方法进行曲面及实体模型网度模拟

(3) 通过底界面Z=0的设定，建立三维空间理论实体模型。借助软件Processes进程下的Utilities模块中Volum calculation功能，可以快速计算得到三维实体模型体积量，理论函数模型体积方量计算误差分析，详见表1。

由表1可以看出，通过合理的插值计算方法和网格密度控制的选择，基于Petrel下的网格化模型体积计算精度不仅远高于国家施工组织设计规范相对误差为3%的计算精度要求[9]，而且还要优于Surfer软件中经理论验证精度最好的改进谢别德法[8]，因此，该软件可以良好地应用于工程施工中土石方量计算,且估算结果相对更为保守可靠，有利于预算决策。

表1 理论函数模型体积方量计算误差分析

2.2 DEM精度评价方法

对于实际数据条件下的高程模拟，本文采用任意点法[10]对等高线插值方法生成的DEM进行质量分析。利用1∶50 000标准图幅地形图以及图幅上原始标注的19个高程控制点。将这些点处的内插高程与实际高程进行数据比较，通过平均误差(MAE)、均方差(RMSE)、拟合优越度(R2)作为评价指标(表2)。

表2 等高线内插算法的误差分析

参照国家测绘局制定的《基础地理信息数字产品1∶10 000，1∶50 000生产技术规程》[11]中DEM精度评定标准，插值算法符合精度要求，山地地貌下格网点高程中误差小于11 m(表3)。证明了该软件下的DEM精确性。

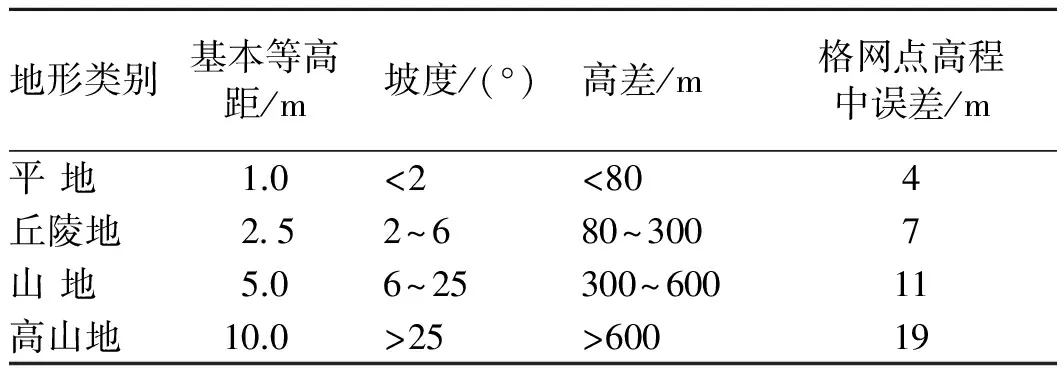
表3 1∶50 000 DEM生产中高程精度要求

3 工程应用

某拟建泵站工程场地占地面积约4 482 m2，场地内地形变化相对较大，海拔高度1 057～1 078 m，相对高差21 m。场地倚山而建，需要实施挖山削坡和低洼填方工作，后进行边坡加固。设计施工形成约1 063 m标高的地坪，同时需要对削坡和填方方量进行分别计算。

通过含有平面直角坐标和高程信息的工作区原始地形测绘资料和场地边界范围的获取，在制图软件下进行地形线信息完整性核对检查，在确认没有地形等信息数据丢失的情况下，导入Petrel软件以形成空间离散点数据。在三维空间的显示下将非地形信息的无效点文件删除(软件将没有高程信息的点数据自动赋值为0)。

利用等高线插值公式形成数字高程模型。并对1 063 m水平作为控制对原始地形进行赋值实现工程场地模拟。以工区范围做为边界，选择合理的插值网格密度(采用1 m×1 m)建立三维网格，并将原始地形及工后地形作为控制建立三维实体模型。提供模型体积计算，泵站场地施工所进行的削坡方量为7 290 m3，填方方量为10 102 m3。结合三维可视化模型，还可以根据实际需要或考虑工程预算的基础上对设计方案进行调整，通过工程预期成果的模拟再现，更好地服务于工程决策。

4 结 论

相对于传统的二维地质数据表达方式，三维地质模型能够清晰准确地表达各种地质现象，通过快速直观地再现地质单元的空间展布及其相互关系，提供了较为便利的工程决策[12]。

本研究通过基于DEM下的Petrel三维可视化模型的建立，经过DEM精度分析验证，证明其网格化模型具有很高的计算精度，精度完全可以满足工程施工中的土石方量计算需要。三维可视化模型不仅可以直观的展示挖填方工程成果，还可以根据工区实际情况等因素重新调整设计方案，合理规划施工进度安排，在提高工作效率的同时还有效降低了工程预算，同时估算结果方量相对更为保守可靠，可以更好地为工程建设的顺利开展而服务。

[1] 王京卫,丁宁,赵同龙.场地平整中土石方量计算的三维可视化方法[J].测绘工程,2006,15(6):15-19.

[2] 张勇,何江达,谢红强.基于3维实体模型的复杂工程场地土石方量的精确计算及可视化研究[J].四川大学学报：工程科学版,2012(S2):117-121.

[3] 陈立华,申明亮,梅亚东.基于DEM的土石方工程量计算研究[J].中国农村水利水电,2007(9):100-102.

[4] 孟永东,徐卫亚,田斌,等.基于分形插值的岩石边坡工程挖填方量估算[J].岩石力学与工程学报,2009,28(S2):3999-4005.

[5] 李洪涛,陈建峰,何宏,等.基于ARCGIS的土石方量计算和调配路径最优化研究[J].矿山测量,2011(5):38-39.

[6] 冯晓刚,刘明星,撒利伟,等.三维激光扫描在土石方量精计算中的应用[J].地理空间信息,2015(4):49-51.

[7] 王宝成,赵锋.填挖方量计算的精度评定[J].测绘通报,2002(11):40-41.

[8] 陈竹安,罗亦泳,张立亭.基于Surfer的土地整理土石方量计算及精度分析[J].工程勘察,2010，38(5):53-56.

[9] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].湖北 武汉:武汉理工大学出版社,2003.

[10] 谭衢霖,徐潇,王浩宇,等.不同地貌类型区DEM空间内插算法精度评价[J].应用基础与工程科学学报,2014,22(1):139-149.

[11] 国家测绘局.基础地理信息数字产品1∶10000,1∶50000生产技术规程[S].北京:测绘出版社,2007.

[12] 曾钱帮,刘大安,张菊明,等.地质工程复杂地质体三维建模与可视化研究[J].工程地质计算机应用,2005(3):29-33.

Fast Implementation of 3D Visualization Modeling Method for Accurate Calculation of Earth-rock Work

ZUO Jianyang1,2, NI Wankui1

(1.SchoolofGeologyEngineeringandGeomatics,Chang’anUniversity,Xi’an，Shanxi710054,China; 2.NingxiaInstituteofLandandResourceInvestigationandMonitoring,Yinchuan,Ningxia750002,China)

[Objective] The method and application of fast accurate calculation of earth-rock work volume were demonstrated to provide effective reference for the engineering design and decision-making arrangements. [Methods] The digital elevation model established by Petrel software was used to realize the 3D precision of earthwork volume. [Results] Through the evaluation of model accuracy, this method not only met the needs of the project, but also was higher than Surfer software. [Conclusion] Combined with the engineering example, the estimation results performed more conservative and reliable. This accurate earthwork calculation can directly demonstrate the expected project results.

earth-rock work; fast calculation; visualization; precision

2016-05-11

2016-05-27

陕西省科技统筹创新工程计划课题“沟谷高填方填筑技术及控制标准研究”(2012KTDZ03-04)

左健扬(1988—),男(汉族),宁夏自治区盐池县人,博士研究生,研究方向为岩土体边坡工程地质。E-mail:zuo_jy@163.com。

10.13961/j.cnki.stbctb.2016.06.023

B

1000-288X(2016)06-0136-03

P282

文献参数： 左健扬, 倪万魁.快速实现三维可视化土石方量精确计算的方法与应用[J].水土保持通报，2016,36(6)：136-138.