基于遗传算法的加权最小二乘支持向量机GPS高程拟合法

李明飞,郇敏,秦川

(1.陕西省土地工程建设集团有限责任公司,西安 710000;2.陕西汇图测绘地理信息有限公司,西安710000)

基于遗传算法的加权最小二乘支持向量机GPS高程拟合法

李明飞1,郇敏2,秦川1

(1.陕西省土地工程建设集团有限责任公司,西安 710000;2.陕西汇图测绘地理信息有限公司,西安710000)

由于GPS高程数据中往往含有粗差,采用最小二乘法进行GPS高程拟合时,无法探测和处理粗差,拟合结果精度较低。本文将加权最小二乘支持向量机应用于GPS高程拟合,并采用遗传算法对参数进行优化。结合实例,对比分析了传统的二次曲面拟合法、最小二乘支持向量机、基于遗传算法的加权最小二乘支持向量机的实验结果,验证了基于遗传算法的加权最小二乘支持向量机方法具有精度高、抗差稳定性强的特点,是一种更为合理的高程拟合方法。

粗差;精度;权函数;参数寻优;遗传算法

0 引 言

最小二乘支持向量机(LSSVM)以支持向量机为基础,用等式约束代替非等式约束,能较好地解决了小样本、非线性、高维数、局部极小点等实际问题[1],并且具有较高的运算效率。李超、任和旺[2]将LSSVM应用到GPS高程拟合中,并通过实验验证了该方法具有较高的精度。但当数据中含有粗差时,该方法的拟合结果受到严重影响。为了克服粗差的影响,本文将加权最小二乘支持向量机引入到GPS高程模型构建,并以遗传算法对模型进行参数优化,抑制或剔除高程数据中含有粗差的点位坐标,提高GPS高程模型的拟合预测精度。

1 加权最小二乘支持向量机

(1)

yk=ωTφ(xk)+b+ek,k=1,2…n,

(2)

其中:ω为权向量;γ为惩罚系数；φ(.)是非线性映射函数,将样本的输入空间映射到高维特征空间;b为偏差量。

根据Lagrange 定理可得:

b+ek-yk},

(3)

根据Karush Kuhn Tucker优化条件[5],先后求出L关于ω,b,e,α的偏导数,并让数值为0.通过整理式子可得矩阵方程:

(4)

根据式(4)求出系数阵α和b,然后求出误差变量的权重vk,重新组成LSSVM-W的目标函数,迭代多次,直至求得稳定的α.

最后,得到LSSVM-W函数估计模型:

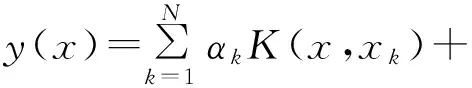
(5)

2 用遗传算法优化加权最小二乘支持向量机的参数(Ga-wlssvm)

遗传算法是由Holland于1975年首次提出来的[8],是基于适者生存的进化论学说和遗传学理论的智能算法[9]的理论。它模拟自然界生物进化的过程, 从任意给定的初始种群出发, 通过遗传学中的选择、交叉和变异, 产生一群更适应环境的个体, 使群体向好的参数区域移动。通过一代代的繁衍进化,群体最后收敛到系统需求的样本个体上,最终得到所寻找的最优值。

用遗传算法优化加权最小二乘支持向量机参数主要步骤为:

1) 遗传算法参数的设置,如群体规模、交叉概率、变异概率、种群的取值范围以及算法终止进化代数。

2) 对C和γ两个参数进行二进制编码,并在参数取值范围内通过随机函数产生一定数目的个体作为进化的初始种群。

3) 对群体中的每一个个体进行适应能力的评价。这里将加权最小二乘支持向量机的预测高程中误差(RMSE)作为目标函数值。RMSE越小,则个体的适应能力就越大;反之,则越小。

4) 根据适应度的大小,按一定的规则选出优秀的下一代,并对部分个体进行交叉、变异操作。

5) 依据当前进化代数判断算法是否终止,如果当前进化代数小于最大遗传代数,则算法重新回到第二步,进行下一次循环;如果当前进化代数大于等于最大遗传代数,则算法终止,输出最优参数值。

3 实验分析

为验证Ga-wlssvm在高程拟合中的有效性和准确性,以某一区域GPS控制网的的实测数据为

例进行计算。该地区长约13.2 km,宽约5.5 km,平均点间距约为2 km,如图1所示,在测区控制点中,最大高程为1 261.831 m,最小高程为1 121.662 m,最大高差140.169 m.控制网共有20个实验点,水准测量采用的三等水准。实验以其中11个均匀分布的点作为拟合点,用其余9个点作为检核点。

图1 GPS点的平面分布

利用Ga-wlssvm进行GPS高程拟合的主要步骤为:

1) 数据处理:采集到的GPS数据数值较大,为避免拟合结果产生影响,需对数据进行平移和缩放处理。

2) 利用实验点的GPS高程和水准数据求出高程异常值。

3) 采用遗传算法对加权最小二乘支持向量机进行参数C和γ优化,求出最优值。

4) 结合参数最优值,构建出加权最小二乘支持向量机模型。

5) 利用模型对未知点的高程异常值进行预测,结合GPS数据求出预测点高程。

在实验中,任意选取拟合点中的一个点为研究对象,依次加入粗差0.05 m、0.1 m、0.2 m和0.5 m.然后分别用传统的二次曲面拟合法、最小二乘支持向量机、和Ga-wlssvm生成GPS高程模型,再对检测点进行预测。实验选取检测点的误差绝对值最大值和中误差来对这三种高程拟合法进行评定,如表1所示。

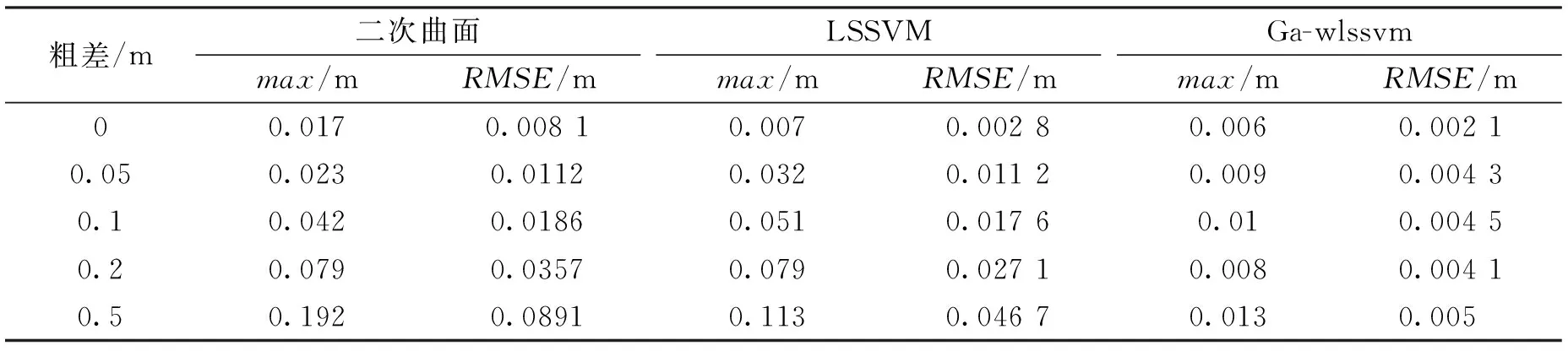
表1 三种方法的对比

从表1中可知,随着粗差的增大,二次曲面法和LSSVM得到的Max和RMSE逐渐增大,说明这两种方法的精度逐渐降低。当粗差为0.2 m时,二次曲面法和LSSVM得到Max均达到了0.079 m,RMSE分别达到了0.035 7 m和0.027 1 m.这两种方法的预测值与实际值相比,均有较大偏差;当粗差为0.5 m时,二次曲面法和LSSVM都已失效;Ga-wlssvm方法得到的RMSE先是随着粗差的增大而增大,后趋于稳定,且均小于前两种方法的结果。通过试验可以看出,Ga-wlssvm精度较高,具有良好的抗差性,可以运用到GPS高程拟合。

4 结束语

本文利用基于遗传算法的加权最小二乘支持向量机拟合法,结合实际工程实际数据,通过与传统的二次曲面拟合法、最小二乘支持向量机拟合法对比,验证了在一定条件下该方法的可行性与精确性。在实验中,Ga-wlssvm拟合方法的核函数为高斯径向基核,权函数为“whampel”,而不同的核函数和权函数都会对实验产生影响,核函数和权函数的选取有待进一步研究。

[1] 方瑞明.支持向量机理论及其应用分析 [M].北京:中国电力出版社, 2007.

[2] 任超,李和旺.最小二乘支持向量机在GPS高程拟合中的应用[J].工程勘察,2012(7):55-57.

[3] 阎辉,张学工,李衍达.支持向量机与最小二乘法的关系研究[J].清华大学学报(自然科学版),2001,41(9):77-80.

[4] 李明飞,陈传法,戴洪磊,等.DEM构建的加权最小二乘支持向量机算法[J].地理空间信息,2015(6):82-83.

[5] 邓乃扬,田英杰.数据挖掘中的新方法——支持向量机[M].北京:科学出版社,2006.

[6] 孙凯,王颖龙.支持向量机中Mercer核函数的构造研究[J].兵工自动化,2008,27(11):40-42.

[7] 叶俊勇.人脸检测与识别方法研究[D].重庆:重庆大学,2002.

[8] HOLLAND J H. Adaptation in natural and artificial System[M]. Ann Arbor: University of Miehigan Press,1975.

[9] 赵义武,牛庆银,王宪成.遗传算法与蚁群算法的融合研究[J].科学技术与工程,2010,10(16):4017-4020.

Application of the Weighted Least Squares Support Vector Machine Based on Genetic Algorithm in GPS Leveling

LI Mingfei1,HUAN Min2,QIN Chuan1

(1.ShaanxiProvincialLandEngineeringConstructionGroup,Xi’an710000,China；2.ShaanxiHuiTumappingGeographicCompany,Xi’an710000,China)

Because of various factors, the elevation data collected by GPS equipment often contain outliers. The least square method often used to GPS elevation fitting, can not detect and handle outliers, so the the accuracy of the fitting results is low. This paper applies the weighted least squares support vector machine to GPS elevation fitting, and uses the genetic algorithm to optimize its parameters. Through the calculation experiment,we compare the experimental result of the quadratic curve fitting, the least squares support vector machine,and the weighted least squares support vector machine based on genetic algorithm,and verify that the weighted least squares support vector machine based on genetic algorithm is a more reasonable elevation fitting method, with characteristics of high precision and stability.

Gross error; accuracy; weight function; parameters optimization; genetic algorithm

2016-08-27

10.13442/j.gnss.1008-9268.2016.06.019

P228.4

1008-9268(2016)06-0098-04

李明飞(1987-)男,助理工程师,研究方向为数字高程模型,目前从事土地整治工作。

郇敏(1987-)女,助理工程师,从事测绘内业处理工作。

秦川(1987-)男,助理工程师,从事土地整治工作。

联系人：李明飞 E-mail: 1045652087@qq.com