基于遗传算法的12自由度动力总成悬置系统多目标优化

樊帆

(广州汽车集团股份有限公司汽车工程研究院，广东广州 511434)

基于遗传算法的12自由度动力总成悬置系统多目标优化

樊帆

(广州汽车集团股份有限公司汽车工程研究院，广东广州 511434)

以某乘用车为研究对象，建立了包括动力总成和车身两个刚体的12自由度动力总成悬置系统模型。以能量解耦及怠速隔振量为目标函数，综合考虑悬置主簧结构及刚体模态频率分布的约束要求，采用遗传算法对动力总成悬置系统解耦率及怠速隔振量进行多目标优化。仿真结果与试验结果表明，该方法能有效优化动力总成悬置系统。

12自由度动力总成悬置系统； 多目标优化； 遗传算法

0 引言

动力总成悬置系统的设计是减小发动机振动与噪声的一项关键技术[1]266。通常通过优化动力总成悬置系统来减少发动机激励引起的整车振动。目前，在汽车悬置系统的优化设计中，最大限度地解除动力总成-悬置系统的多自由度振动耦合是使其具有良好隔振性能的基本方法[2]。能量解耦率方法作为一种有效的振动解耦方法已被广泛用于动力总成悬置的设计和优化中[3]。怠速隔振量指标主要用于验证阶段装车后采用实测的方法对悬置系统的评价。由于动力总成悬置系统的解耦率和怠速隔振量两个性能指标相对独立，所以一套隔振效果好的悬置系统一般要经过多轮的悬置系统优化与试验，周期长，成本高[4-5]。文中考虑车身质量惯性参数、悬架刚度的影响因素，建立包括动力总成和车身两个刚体组成的12自由度动力总成悬置系统模型，综合考虑解耦率和怠速隔振量，应用NSGA-II遗传算法[6]，对某乘用车动力总成悬置系统进行多目标优化。

1 系统建模

1.1 12自由度悬置系统模型

文中研究的乘用车动力总成为前置，悬置系统采用三点悬吊式布置。在研究动力总成悬置系统隔振性能时，将动力总成及车身简化为刚体，3个悬置简化为3个相互垂直的线性弹簧黏性阻尼元件，悬置支承在车身上，由于怠速时悬架属于微幅振动，变形量很小，可以使用前后悬架静平衡位置的垂向刚度作为模型的悬架垂向刚度；悬架系统简化为3个相互垂直的线性弹簧元件，此处假定为车身通过4个悬架弹簧连接在刚性的质量无限的基础上。动力总成及车身分别有6个自由度，即x、y、z三向平动及绕x轴、y轴、z轴的转动，由此构成12自由度的动力总成悬置系统模型，如图1所示。

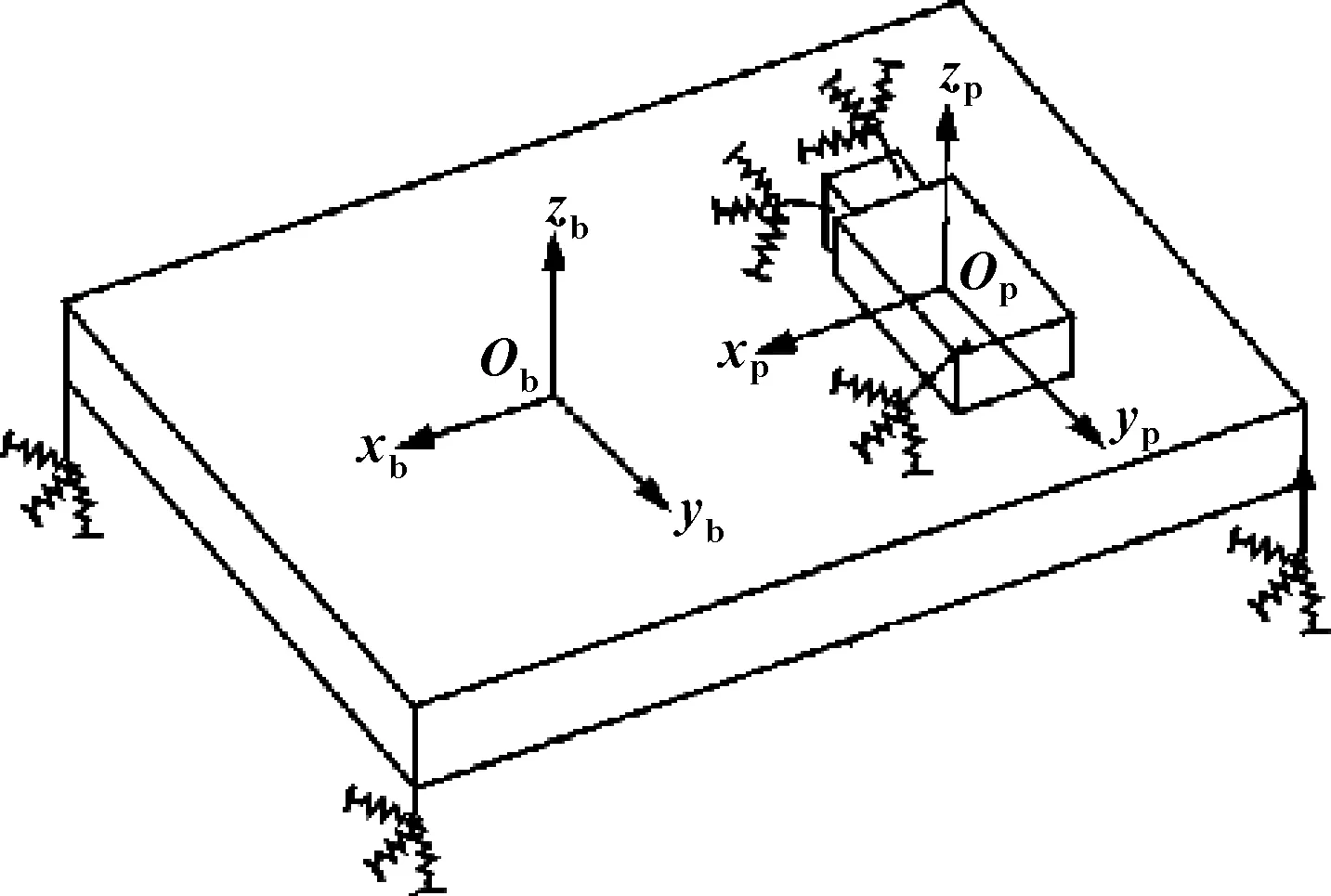
图1 12自由度悬置系统模型

其动力学表达为：

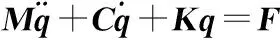
(1)

式中：M=[mp,mp,mp,Jpx,Jpy,Jpz,mb,mb,mb,Jbx,Jby,jbz]，包括动力总成及车身的质量惯性参数；q=[xp,yp,zp,θx,θy,θz,xb,xb,xb,φx,φy,φz]，为广义坐标向量；C为系统阻尼矩阵；K为系统刚度矩阵；F为发动机激励向量。

1.2 系统参数

12自由度模型所需的输入参数包括以下部分：动力总成质心、悬置弹性中心在整车坐标系中的坐标及倾角如表1所示；实测动力总成质量、转动惯量及惯性积如表2所示。车身定义为整车除去前悬、后悬、动力总成部分，车身质量、转动惯量及惯性积如表3所示；前悬架、后悬架垂向刚度如表4所示，由于悬架实际的横向与纵向刚度较大，取横向刚度与纵向刚度为垂向刚度的100倍[7]。

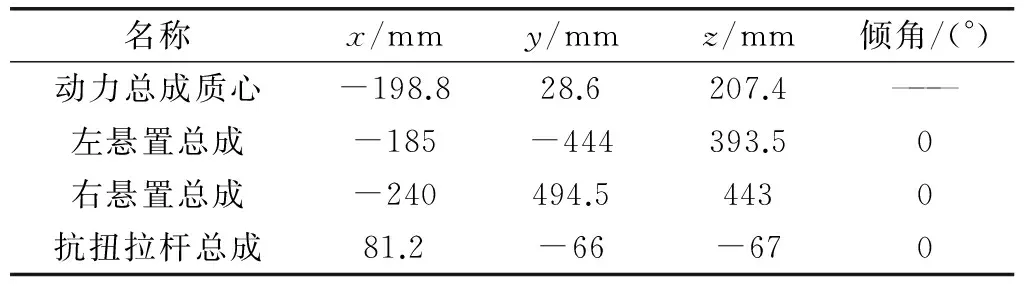
表1 质心及悬置弹性中心坐标

表2 动力总成的质量惯性参数

表3 车身的质量惯性参数

表4 悬架垂向刚度 N·mm-1

2 遗传算法优化分析

NSGA-II算法是一种基于快速非劣性排序的改进型多目标遗传算法。其高效性在于运用一个推支配分类程序，使多目标简化到一个适应度函数的方式，该方法能解决任意数目的目标问题，且能求解最大和最小的问题，在工程中有广泛的应用。基于NSGA-II求解发动机悬置系统的多目标优化问题按如下步骤进行。

2.1 设计变量

由于抗扭拉杆为沿用件，这里以左悬置3个方向刚度kxi、kyi、kzi,右悬置3个方向刚度kxj、kyj、kzj6个变量为初始变量。

2.2 约束条件

(1)设计约束包括动力总成悬置系统垂向及绕曲轴方向刚体模态的频率与其余模态的频率间隔在1 Hz以上，其他模态频率之间的间隔在0.8 Hz以上；

(2)垂向模态频率位于8～9 Hz之间；

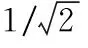
(4)由于悬置橡胶结构固定，左悬置主簧结构见图2、右悬置主簧结构见图3，综合考虑工艺及结构，3个方向刚度比具有如下约束：

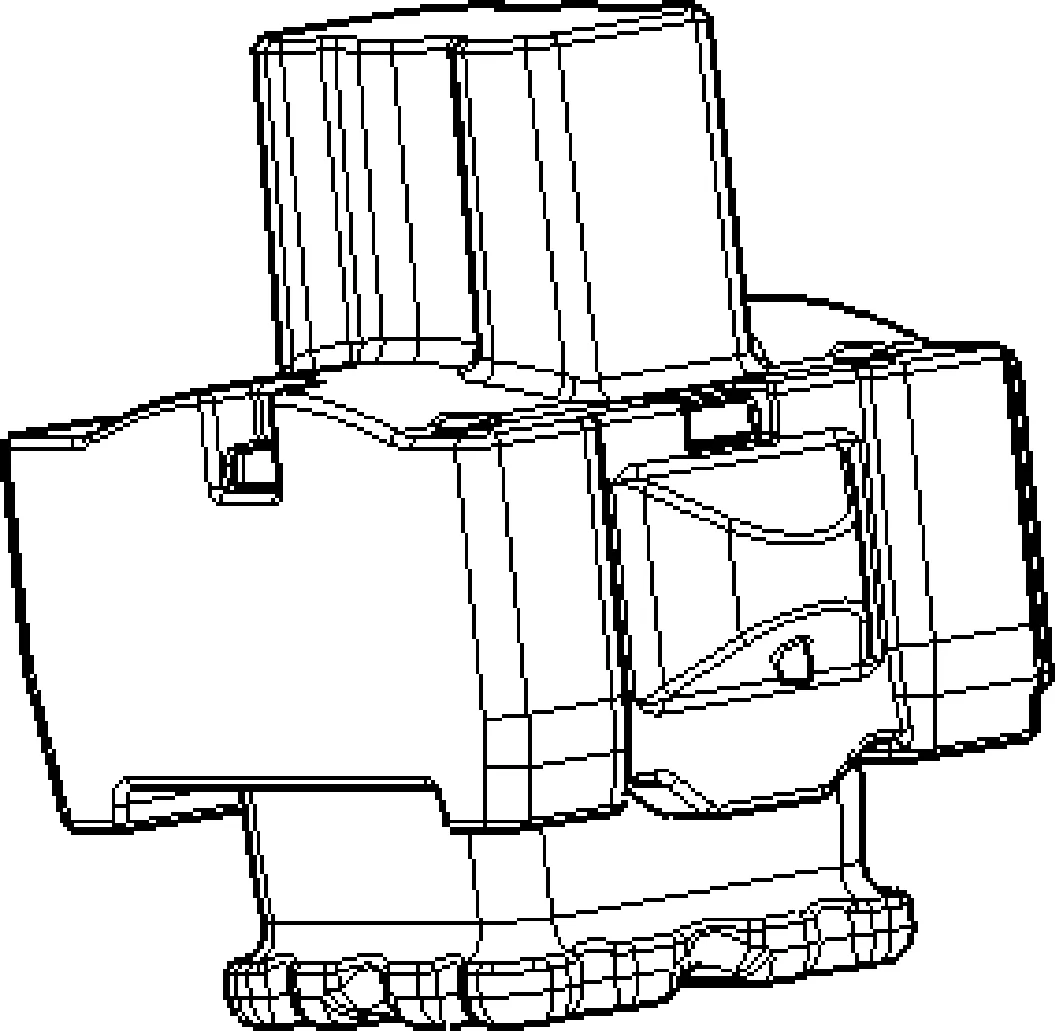
图2 左悬置主簧结构

图3 右悬置主簧结构

2.3 优化目标

设计要求各方向解耦率目标为不小于85%。以动力总成悬置系统各个方向的解耦率最大，以左悬置、右悬置3个方向的怠速隔振量最大为优化目标。

用怠速时动力总成输出的转矩值，在发动机质心处施加稳定周期激励，在悬置主动端同样会产生一个与激励频率相同的加速度响应。在主动端激励幅值一定的情况下，悬置被动端加速度幅值决定了悬置隔振量的大小，被动端加速度越小，隔振量越大。因此，以怠速时左悬置、右悬置被动端3向加速度的RSS(平方和的平方根)值最小作为优化目标。

设动力总成的质量矩阵为M，当动力总成悬置系统以第i阶固有频率fi(fi=ωi/2π)和振型φi=[φ1i,φ2i,φ3i,φ4i,φ5i,φ6i,]T振动时，第k个广义坐标上的能量E(k,i)， 即能量解耦率为：

(2)

式中：φli为φi的第l个分量。

E(k,i)反映了系统作i阶振动时，第k个广义坐标与其他坐标的耦合程度。

(3)

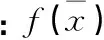
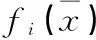
(4)

另外两个目标为怠速时左悬置、右悬置3个方向被动端振动加速度RSS值最小：

(5)

(6)

式中：aLH为左悬置被动端振动加速度RSS值；aLHx、aLHy、aLHz分别为左悬置x、y、z3个方向的被动端振动加速度值；aRH为右悬置被动端振动加速度RSS值；aRHx、aRHy、aRHz分别为右悬置x、y、z3个方向的被动端振动加速度值。

3 仿真分析

3.1 初始数据分析

给出各悬置初始刚度及动静比数据，如表5所示。

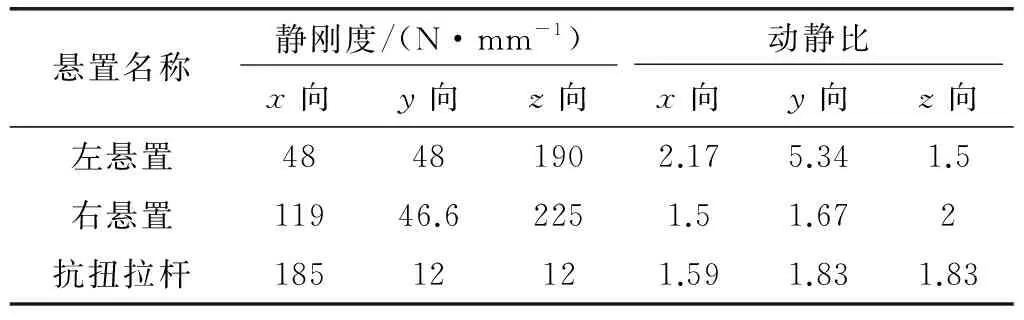
表5 悬置初始静刚度及动静比

初始状态的能量解耦率如表6所示，由分析结果可知：初始刚度下悬置系统能量解耦在z方向以及绕x轴方向低于85%，y向刚体模态低于6 Hz，不满足悬置系统设计目标要求。

表6 初始固有频率及解耦率

3.2 优化分析

利用多目标遗传算法NSGA-II进行优化，悬置刚度优化结果如表7所示。

表7 优化后悬置刚度

优化后解耦率及隔振情况如表8所示，z向以及绕x轴方向解耦率均提高到85%以上，结果符合设计要求。

表8 优化后频率及解耦率

仿真时将怠速时重力和等效扭矩加到动力总成模型上，得到左悬置被动端加速度优化前后对比(如图4所示)和右悬置被动端加速度优化前后对比(如图5所示)。

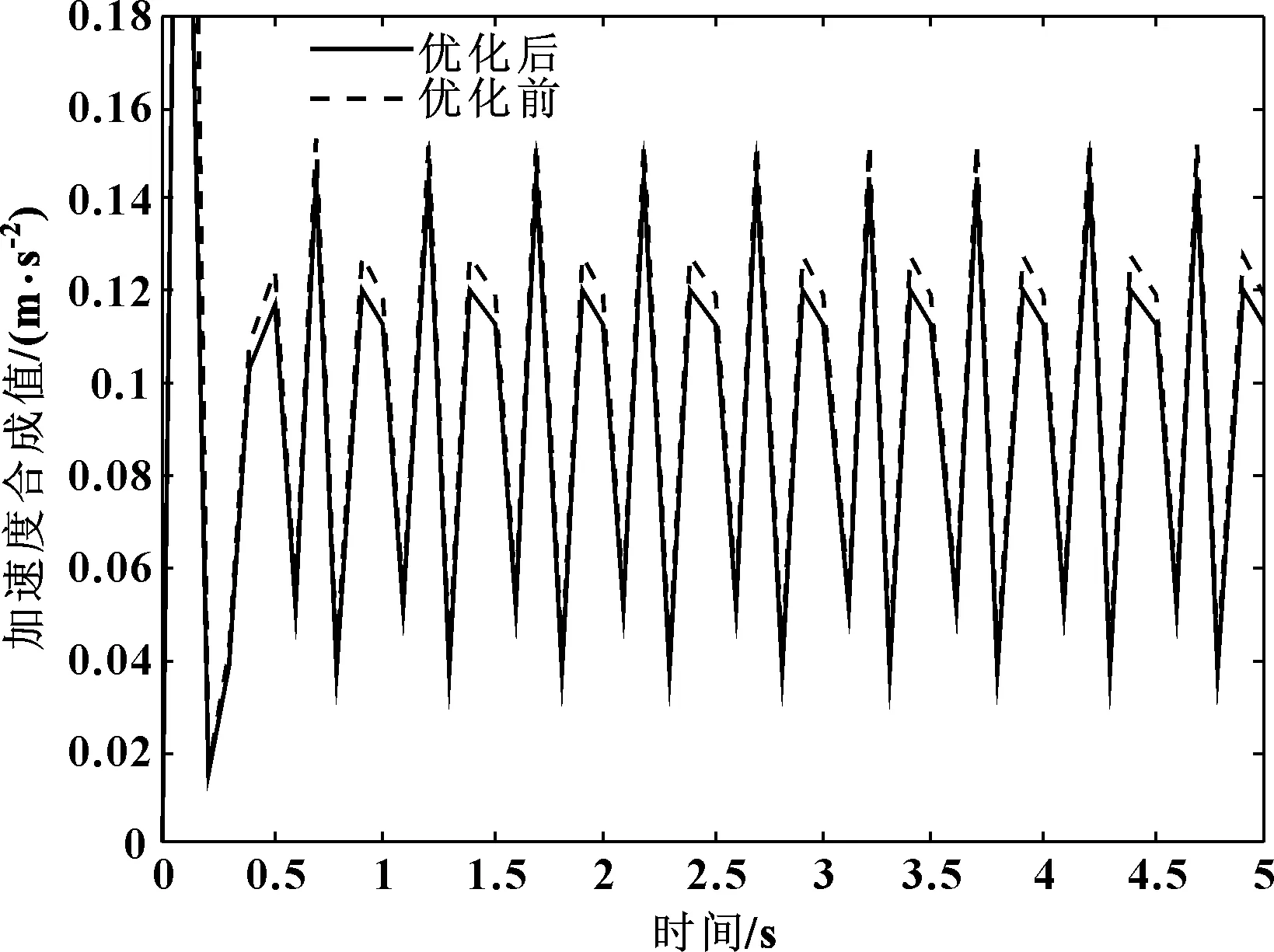
图4 左悬置被动端加速度优化前后对比

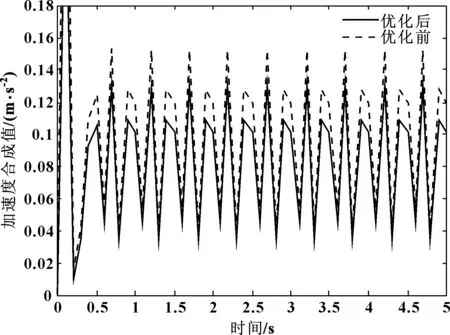
图5 右悬置被动端加速度优化前后对比

由图4可知：左悬置被动端加速度优化后较优化前峰值从0.144 m/s2减少到0.135 m/s2，减少6.25%。由图5可知：右悬置被动端加速度优化后较优化前峰值从0.153 m/s2减少到0.131 m/s2，减少14.3%。

4 试验验证

为验证优化方案的有效性，将原方案悬置及优化后悬置分别装车进行P挡怠速状态下悬置主动端、被动端x、y、z3个方向振动情况测试，左悬置、右悬置隔振测试布线分别如图6、图7所示。其中动力总成悬置隔振量计算公式为：

(7)

式中：aactive为主动端振动加速度，apassive为被动端加速度，单位m/s2。

图8、图9、图10分别为优化后左悬置x、y、z3个方向隔振测试曲线，图11、图12、图13分别为优化后右悬置x、y、z3个方向隔振测试曲线，为便于观察各悬置在不同频率段隔振性能，将纵坐标以隔振量形式表示。

图6 左悬置隔振测试布线图

图7 右悬置隔振测试布线图

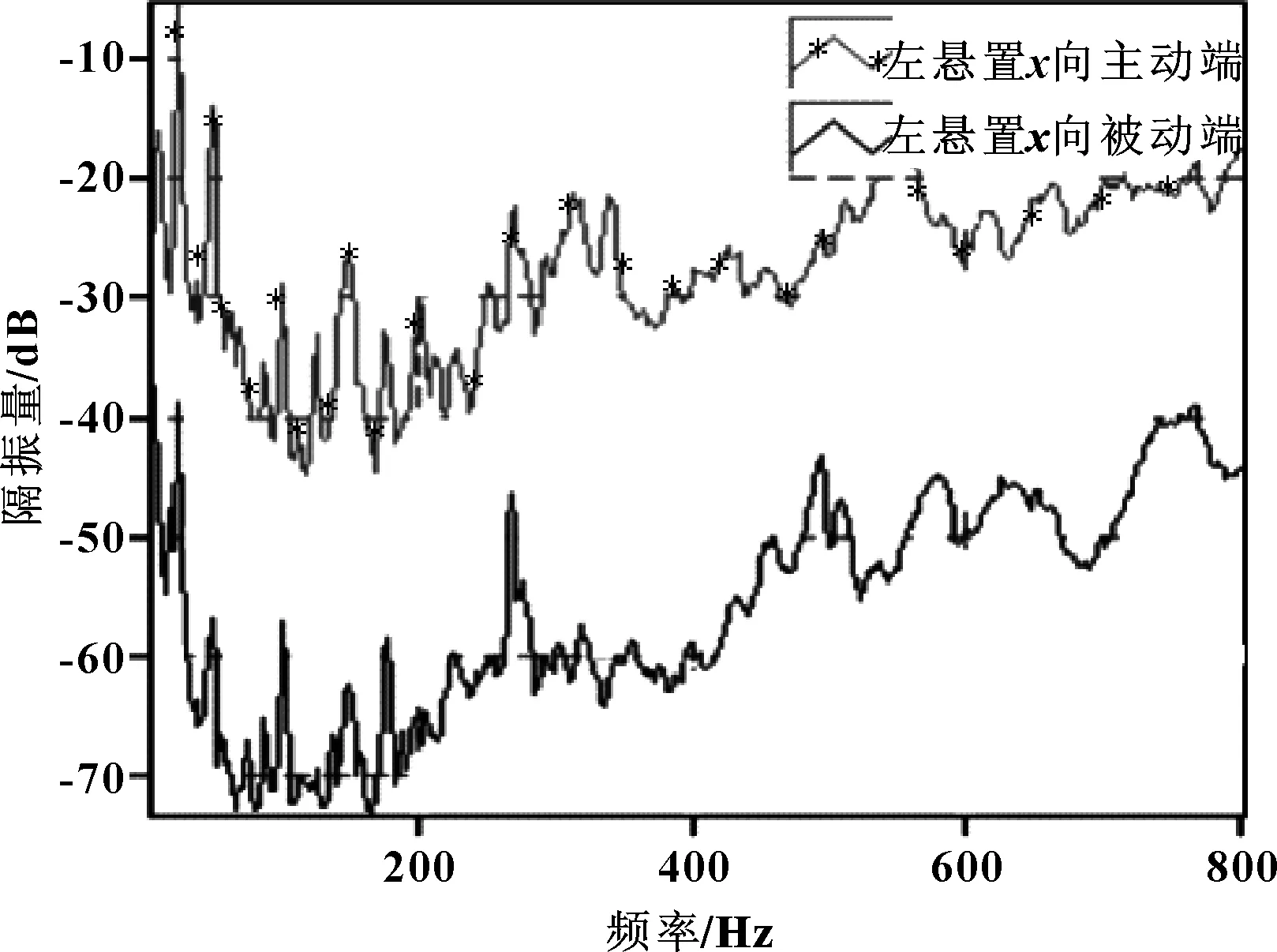
图8 优化后左悬置x向隔振曲线

图9 优化后左悬置y向隔振曲线

图10 优化后左悬置z向隔振曲线

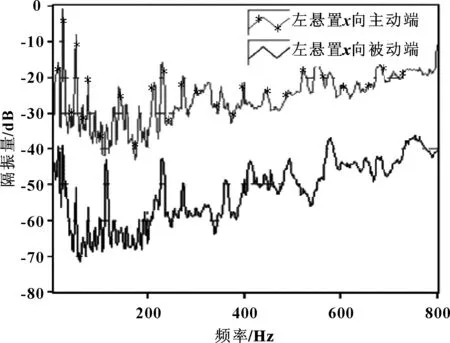
图11 优化后右悬置x向隔振曲线

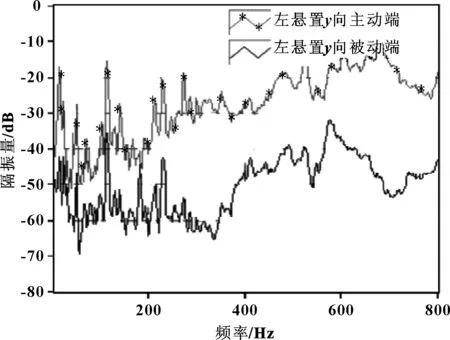
图12 优化后右悬置y向隔振曲线

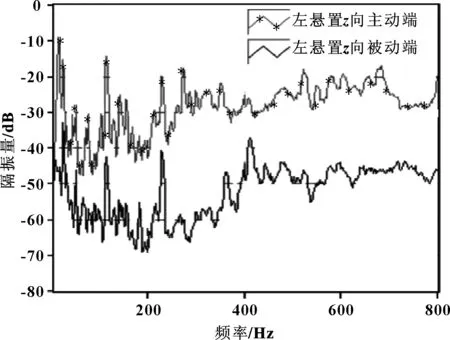
图13 优化后右悬置z向隔振曲线

根据以上测试数据，可得到左悬置隔振情况如表9所示，优化后的左悬置被动端加速度RSS值由0.113 m/s2降低到0.091 m/s2，怠速隔振量在x方向由25.7 dB提高到27.04 dB、y方向由24 dB提高到25.83 dB、z方向由18.5 dB提高到20.75 dB。

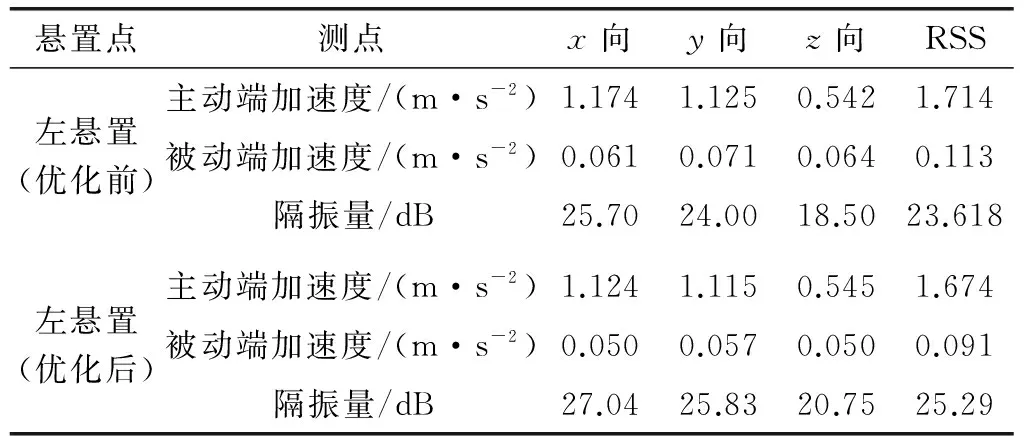
表9 优化前后左悬置隔振量

得到右悬置隔振情况如表10所示，优化后的右悬置被动端加速度RSS值由0.149 m/s2降低到0.111 m/s2，怠速隔振量在x方向由25.22 dB提高到30.22 dB、y方向由23.38 dB提高到29.25 dB。虽然z方向由23.36 dB下降到21.14 dB，一般认为振动的衰减率应该在20 dB以上，即TdB>20 dB，就具有良好的隔振效果[1]280。并且优化后3个方向的RSS值隔振从24.09 dB提高到26.59 dB，因此认为左悬置、右悬置优化方案有效。

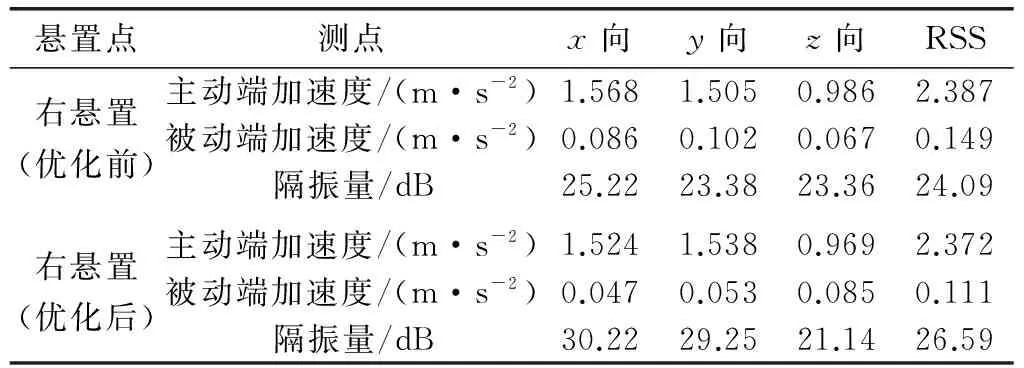
表10 优化前后右悬置隔振量

5 结束语

(1)建立12自由度动力总成悬置系统模型，以此模型为基础模拟出悬置系统的能量解耦率、刚体模态频率分布以及悬置系统怠速振动情况；

(2)运用NSGA-II遗传算法对12自由度悬置系统进行多目标优化，使悬置系统的能量解耦以及刚体模态频率分布达到设计要求，有效降低左悬置、右悬置的被动端加速度，试验表明该优化方法能有效提高左悬置、右悬置的隔振量。

【1】庞剑，谌刚，何华.汽车噪声与振动:理论与应用[M].北京：北京理工大学出版社，2006.

【2】吕振华，范让林.动力总成-悬置系统振动解耦设计方法[J].机械工程学报，2005,41(4):49. LV Z H,FAN R L.Design Method for Vibration Uncoupling of Powerplant Mounting System[J].Chinese Journal of Mechanical Engineering,2005,41(4):49.

【3】孙蓓蓓，张启军，孙庆鸿，等.汽车发动机悬置系统解耦方法研究[J].振动工程学报，1994(7)：240-245. SUN B B,ZHANG Q J,SUN Q H,et al.Study on Decoupled Engine Mounting System[J].Journal of Vibration Engineering,1994(7)：240-245.

【4】吴飞，胡朝辉，成艾国，等.综合考虑解耦率和隔振率的发动机悬置系统多目标优化[J].汽车工程，2013，35(1)：18. WU F,HU C H,CHENG A G，et al.The Multi-objective Optimization of Engine Mount System Concurrently Considering Energy Decoupling Rate and Vibration Isolation Rate[J].Automotive Engineering,2013，35(1)：18.

【5】张健，杨啟梁，胡溧，等.基于ADAMS的12自由度动力总成悬置系统怠速隔振分析[J].汽车技术，2013(1)：38. ZHANG J,YANG Q L,HU L,et al.Idle Vibration Isolation Analysis of Twelve Degrees of Freedom Power-train Mounting System Based on ADAMS[J].Automobile Technology,2013(1)：38.

【6】CHEN S,SHI T，WANG D,et al.Multi-objective Optimization of the Vehicle Ride Comfort Based on Kriging Approximate Model and NSGA-II[J].Journal of Mechanical Science and Technology,2015,29(3):1007-1018.

【7】郭正康.汽车整车转动惯量的计算与选取[J].汽车研究与开发，1993(6)：42-44.

【8】周密，侯之超.基于遗传算法的动力总成悬置系统优化设计[J].汽车技术，2006(9)：14-15. ZHOU M,HOU Z C.Optimization on Engine Mounting Based on Genetic Algorithm[J].Automobile Technology,2006(9)：14-15.

Multi-objective Optimization of Twelve Degrees of Freedom Powertrain Mounting System Based on Genetic Algorithm

FAN Fan

(Automotive Engineering Institute, Guangzhou Automobile Group Co.,Ltd., Guangzhou Guangdong 511434，China)

Taking a car as study object, a dynamic model of twelve degrees of freedom powertrain mounting system was established which included powertrain and body.Taking energy decoupling rate and vibration isolation in idle as objective functions, considering the main spring structure and frequency distribution of rigid body as constraint conditions, multi-objective optimization aiming at energy decoupling rate and vibration isolation of the powertrain mounting system was carried based on genetic algorithm. The results of simulation and real vehicle test verify the effectiveness of the method proposed.

Twelve degrees of freedom powertrain mounting system;Multi-objective optimization;Genetic algorithm

2016-09-05

广东省科技厅省部产学研结合基金资助项目(2013B090400002)

樊帆，硕士，工程师，目前从事汽车底盘设计研发工作。E-mail:fanfan@gaei.cn。

10.19466/j.cnki.1674-1986.2016.12.002

U461.2

A

1674-1986(2016)12-007-05